列车车轴空间直线度检测

王华 侯岱双 张爽 高金刚

摘 要：为了准确、快速地测量列车车轴的空间直线度，构建了列车车轴空间直线度测量系统，对所述测量系统采用的空间圆拟合、空间直线拟合、直线度测量等算法进行研究。首先，根据被测对象的特征介绍了基于空间平面与空间球相切空间圆拟合算法;然后，利用随机采样一致性（RANSAC）算法迭代出符合模型的最佳点集，在列车车轴截面空间圆拟合获取的数据基础上对列车车轴截面空间圆圆心所处数据进行分析，并利用狼群算法拟合空间直线，即通过空间截面所处位置的列车车轴截面空间圆的圆心坐标拟合列车车轴空间直线;最后，利用狼群算法对列车车轴空间直线度进行测量，并把测量数据与激光跟踪仪数据进行对比。实验结果表明：基于狼群算法的列车车轴空间直线度测量精度为0.01mm，能够满足列车车轴空间直线度测量的高精度、高稳定性及测量重复性等要求。

关键词：狼群算法;空间圆拟合;空间直线拟合;直线度;测量系统

中图分类号：TP391

文献标志码：A

Abstract： In order to accurately and quickly measure the spatial straightness of train axle， a measurement system of train axle spatial straightness was constructed and the algorithms of spatial circle fitting， spatial straight line fitting and straightness measurement were studied. Firstly， the spatial circle fitting algorithm based on spatial plane and spatial sphere tangent was introduced according to the characteristics of the object under test. Then， the RANdom SAmple Consensus （RANSAC） algorithm was used to iterate out the best point set of the model. On the basis of the data obtained from the spatial circle fitting of the train axle section， the data of the train axle section spatial circle center was analyzed. And the wolf colony algorithm was used to fit the spatial straight line， that is， according to the circle center coordinates of the spatial circle of the train axle section at the position of the space section， the spatial straight line of the train axle was fitted. Finally， the wolf colony algorithm was used to measure the spatial straightness of train axle， and the measured data were compared with the data of laser tracker. Experimental  results show that the accuracy of measuring the spatial straightness of train axle based on wolf colony algorithm is 0.01 mm， which can meet the requirements of high accuracy， high stability and repeatability in measurement of the spatial straightness of train axle.

Key words： wolf colony algorithm; spatial circle fitting; spatial straight line fitting; straightness; measurement system

0 引言

隨着轨道交通行业的迅猛发展，轨道列车成为了人们重要的出行方式之一。车轴是承载轨道列车车身载荷的主要部件，承载着来自车体、轨道和车轮等各方面的载荷，并且车轴也传递着车轮前进的动力，同时车轴加工精度的好坏直接决定着列车的运行安全[1]。因此对列车车轴的加工尺寸进行精密测量与检验成为保障列车安全运行的重要环节。

轨道列车上应用的大型列车轴类零件的测量方式可分为接触式测量和非接触测量。接触式测量包括常规的形状误差检测方法是利用数字千分尺或特定的测量设备进行测量等方法，但这种接触式测量会对轴件造成轻微划痕，引起测量误差。而能够避免轴件划伤的非接触测量，逐渐应用到列车车轴的检测之中。近年，国内外学者针对列车车轴空间直线度检测进行了大量研究，李一男等[2]利用数字千分表建立小尺寸零件的直线度误差检测系统，精度为0.0017mm，其测量目标较小，不适用于大尺寸的列车车轴测量。余晓芬等[3]利用时域三点法对大尺寸长轴进行二维直线度检测，其精度约为0.03mm，但列车车轴为阶梯轴，其测量方法具有局限性。冉成荣等[4]用线结构光对动车车轴进行检测，车轴轴身恢复误差为-0.08～0.07mm，不能得出直线度等参数。邱德超等[5]建立了PEIV（Partial Errors-In-Variables）模型，使得理论模型更为合理，并且在且求解编程计算中更为简便。袁周等[6]设计了一种火车车轴轴径测量检测装置，但该测量装置容易受到系统波动误差的影响，容易导致数据失真。吴呼玲[7]验证了蒙特卡罗方法在直线度误差评定问题上的可行性。陈君宝等[8]利用变步长天牛须搜索算法进行直线度评定，比较了几种方法在直线度测量上的收敛性、运算效率等。本文将狼群算法应用于列车车轴空间直线度检测之中，建立了列车车轴空间直线度测量系统，并讨论了测量中的空间圆拟合算法、空间直线拟合算法、直线度测量算法等列车车轴空间直线度测量系统关键算法。实验结果表明，列车车轴空间直线度测量系统在列车车轴的测量中能够实现对列车车轴测量精度的要求，同时它具有速度快、精度高、结果可靠性等特点。

1 列车车轴空间直线度测量系统

1.1 系统的硬件组成

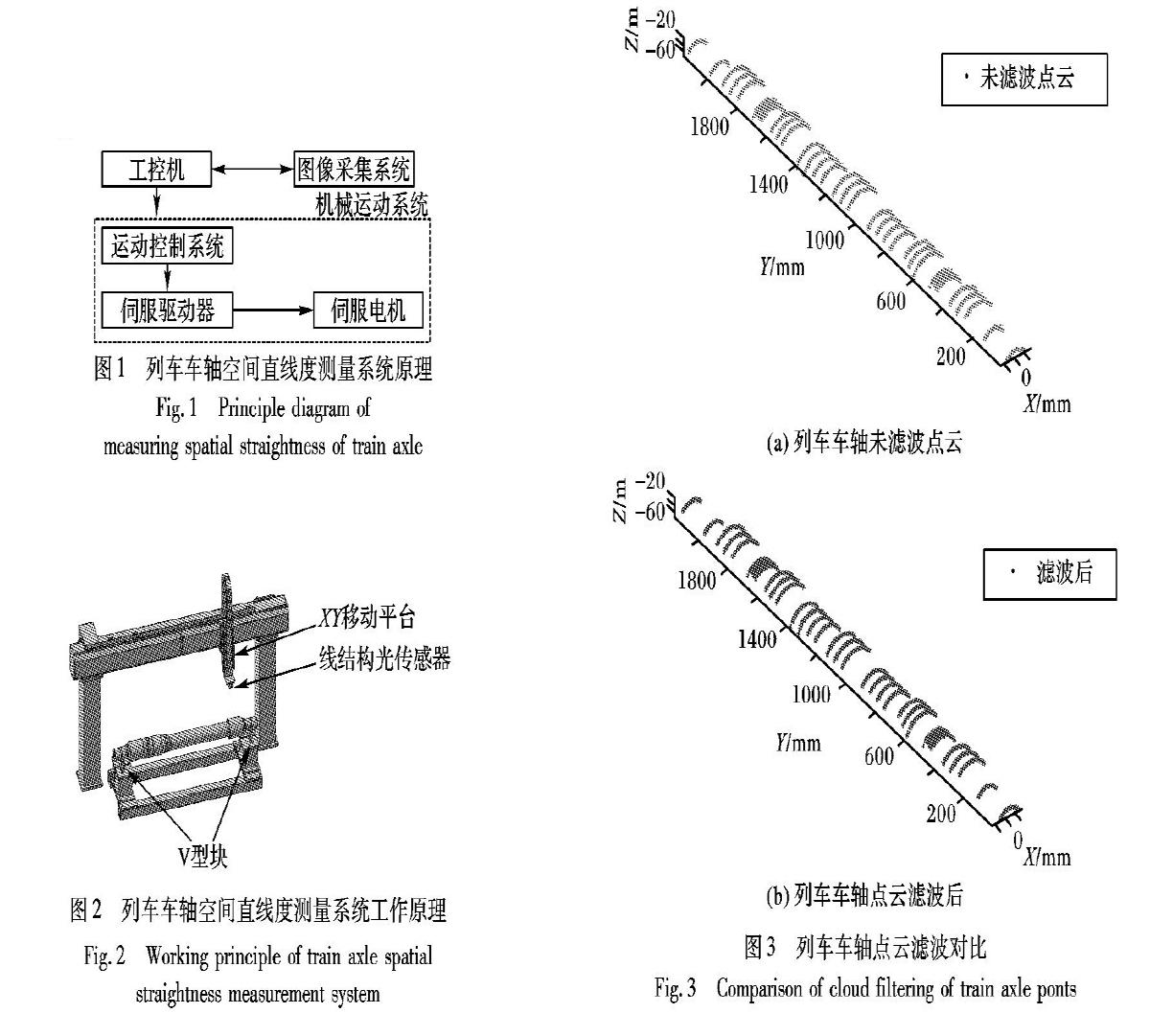
列车车轴空间直线度测量系统原理如图1所示，它主要由图像采集系统、机械运动系统以及工控机等组成。图像采集系统由线结构光传感器和图像采集卡等组成。机械运动系统由XY移动平台、测量系统立柱、测量系统底座、工件支撑座（V型块）和伺服运动系统等组成。当被测工件（即列车车轴）放置在工件支撑座上后，由运动控制系统和光栅尺进行精确定位，根据被测要求对工件进行采集，线结构光传感器采集的数据经由图像采集卡上传到工控机，并由软件对所采集数据进行处理。

1.2 系統的工作原理

本文系统的工作原理如下：列车车轴空间直线度测量就是通过激光传感器获取被测工件的相关图像，然后对图像进行预处理，通过基于狼群的直线拟合方法及直线度测量方法对列车车轴的直线度进行测量。图1的机械运动系统是用来运动XY移动平台和线结构光传感器，在软件的控制下，对列车车轴进行测量，并得出相关测量数据。

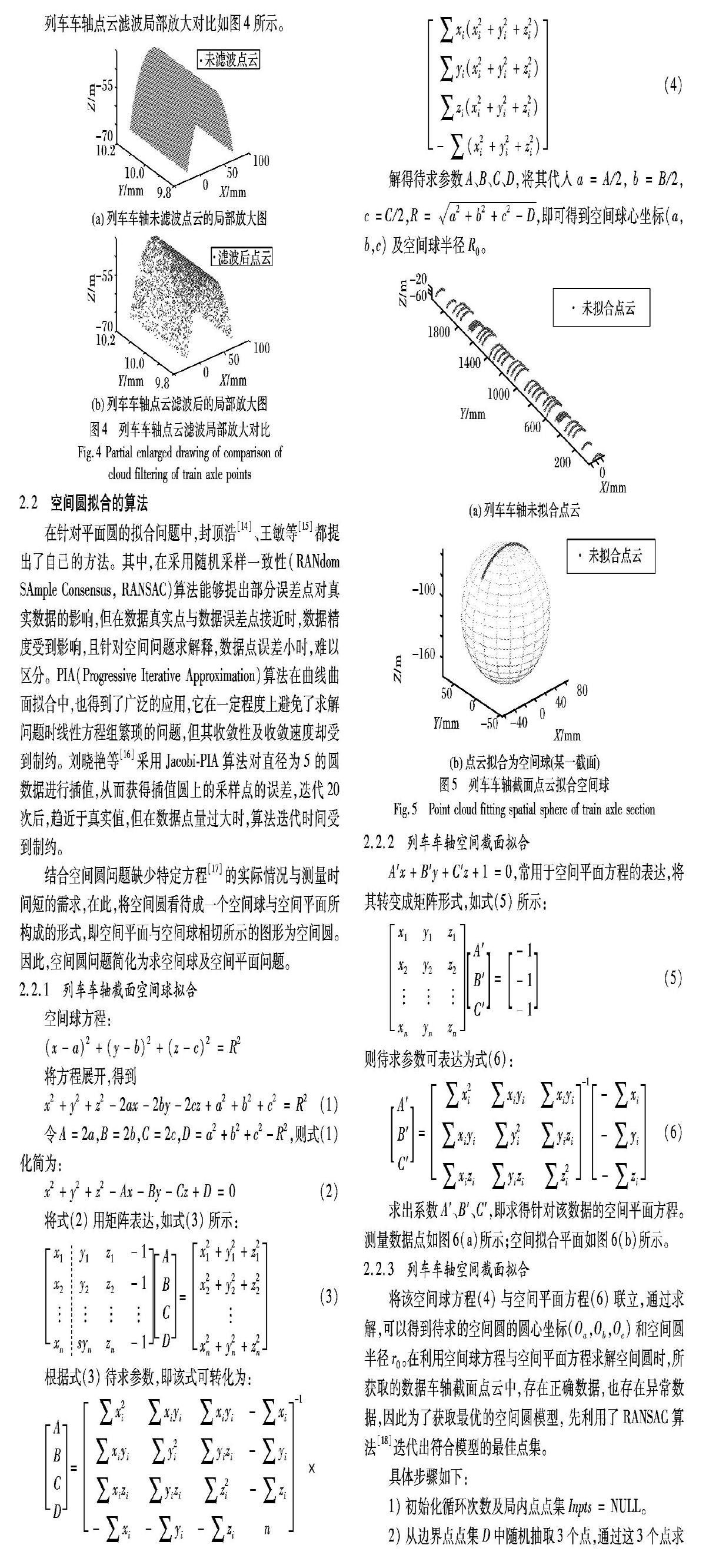
图2中V型块，使车轴保持悬空状态，且保证整个测量过程中列车车轴无位移，以达到高精度测量的目的。图2所示的XY移动平台为高精密平台，且贴有光栅尺，从而保证运动的精度及运动重复性。列车车轴空间直线度测量软件需要实现的功能包括对线结构光传感器所获取的数据进行预处理，

对数据进行空间椭圆拟合、空间直线拟合，及直线度的评定算法。

2 车轴空间直线度测量的关键算法

2.1 车轴点云数据的预处理

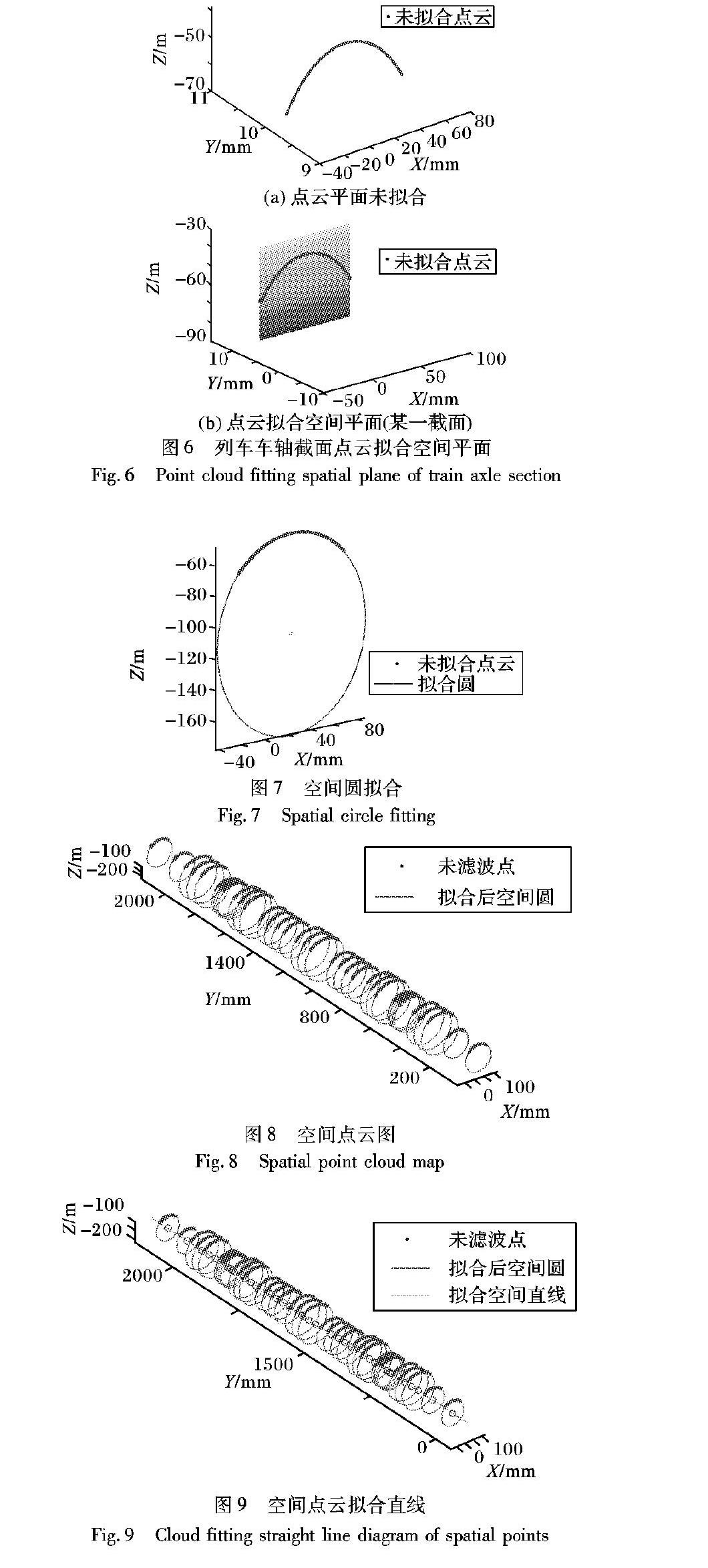
在线结构光传感器对工件（车轴）测量截面轮廓信息时，由于测量环境及长距离等因素会引起扫描点异常，只有将这些异常点去除，才能有效地利用由线结构光传感器获取的扫描数据[9]。而常用的点云滤波方法包括拟合法[10]、聚类/分割算法[11]、基于地形坡度方法[12]等。

通过线结构光传感器获取的点云数据，在处理时，误差主要来源于Y、X和Z方向用于确定传感器所获取的空间圆轮廓所处的平面位置。因此，在针对列车车轴空间数据处理时，本文建立一个四层以点云的三坐标中的X和Z方向点云数据作为输入，Y方向点云作为训练后的期望结果输出。通过BP网络的训练，将期望数据与实际数据对比，剔除超出误差允许范围的噪声点，并将去噪后的点云数据通过mat文件导出保存，实现预期的去噪目的。根据列车车轴截面点云的特点，选取以下函数作为BP网络训练的基本函数。

2.2 空间圆拟合的算法

在针对平面圆的拟合问题中，封顶浩[14]、王敏等[15]都提出了自己的方法。其中，在采用随机采样一致性（RANdom SAmple Consensus， RANSAC）算法能够提出部分误差点对真实数据的影响，但在数据真实点与数据误差点接近时，数据精度受到影响，且针对空间问题求解释，数据点误差小时，难以区分。

PIA（Progressive Iterative Approximation）算法在曲线曲面拟合中，也得到了广泛的应用，它在一定程度上避免了求解问题时线性方程组繁琐的问题，但其收敛性及收敛速度却受到制约。刘晓艳等[16]采用Jacobi-PIA算法对直径为5的圆数据进行插值，从而获得插值圆上的采样点的误差，迭代20次后，趋近于真实值，但在数据点量过大时，算法迭代时间受到制约。

结合空间圆问题缺少特定方程[17]的实际情况与测量时间短的需求，在此，将空间圆看待成一个空间球与空间平面所构成的形式，即空间平面与空间球相切所示的图形为空间圆。因此，空间圆问题简化为求空间球及空间平面问题。

2.2.2 列车车轴空间截面拟合

将该空间球方程（4）与空间平面方程（6）联立，通过求解，可以得到待求的空间圆的圆心坐标（Oa，Ob，Oc）和空间圆半径r0。在利用空间球方程与空间平面方程求解空间圆时，所获取的数据车轴截面点云中，存在正确数据，也存在异常数据，因此为了获取最优的空间圆模型，先利用了RANSAC算法[18]迭代出符合模型的最佳点集。

具体步骤如下：

1）初始化循环次数及局内点点集Inpts=NULL。

2）从边界点点集D中随机抽取3个点，通过这3个点求解出圆的参数，即圆心（Oa，Ob，Oc）、半径r0。

3）计算各边界点到第2）步中所得到的圆的圆心的距离d，若d-r0≤ε，则将点计入局内点集;否则视为局外点。

4）计算该圆上的局内点的个数，记为M，若M大于阈值Mmin，则认为此次估计成功转第5）步;否则转第6）步。

5）对点集Inpts中的所有点用最小二乘法重新计算圆的参数模型，得到最终结果。

6）k=k+1，若k>kmax，则结束; 否则转 2）。

最终单截面拟合效果如图7所示。

2.3 列车车轴空间直线拟合算法

2.3.1 问题转换针对2.2节中获取的空间圆圆心坐标进行空间直线拟合（即列车车轴轴线），空间直线的标准方程为：

在求解空间直线拟合的算法中，目前常用的空间直线拟合的方法有：迭代法[19]和无迭代法[20]。由于y方向为非轴径截面方向，本文采用经上文所述滤波方法后，忽略yi方向误差，并利用无迭代算法进行推理，将空间问题转变成为平面问题，即可将式（7）整理为：

2.3.2 基于狼群算法的直线拟合

头狼、探狼、猛狼等构成了一个主体自上而下的群体[21]，即狼群。狼群通过三种类型狼之间的配合，完成一次次捕猎行动，而狼群中又是残酷的，“由强到弱”“胜者为王”等思想又促使狼群向着再次获取猎物的方向发展，从而保证种群得以生存。狼群算法由探狼寻找猎物游走、头狼发现猎物召唤、猛狼协助头狼围攻，这三种基本的生活行为以及“胜者为王”的头狼角逐规则和“强者生存”的狼群更新规则构成。

Step1：假设狼群规模大小为N，待拟合空间坐标点集为D，则狼群领地可以被抽象为N×D的欧氏空间，算法最大迭代次数为iters，探狼最大游走次数Tmax。

Step2：选取针对目标函数的最优解值的人工狼i作为头狼的当前位置;除去头狼i外的S匹人工狼作为探狼，在N×D的空间中进行搜索，若探狼j发现自己所处位置的目标函数值Yj>Ylead，则探狼j代替头狼发起召唤行为，或游走次数T>Tmax后，转Step3。

Step3：猛狼按照头狼指令奔袭围攻，猛狼按照头狼指令奔袭围攻目标，如果在奔袭过程中，奔袭沿途的猛狼Yk

Step4：当在赶往参与围捕的猛狼与目标函数值距离达到预期区间时，协同探狼对目标猎物进行攻击，以实现捕获。围捕过程中，其他人工狼的Yi>Ylead时，对头狼所在的位置进行更新，直到捕获猎物为止。

Step5：“强者生存”，当狼群中存在的目标函数较小的人工狼，依照原则，予以淘汰，并在解空间中随机生成新的人工狼，并对整个狼群更新。

Step6：判断是否所有点距离都与拟合直线处于最优状态，若满足则输出结果;若不满足则重复Step2～5。

在狼群算法中，初始点云数据经过2.2.3节所述方法的预处理，获取的空间点云数据在满足测量精度要求的同时，也在一定程度上减少了噪声对点云数据的影响。因此，在对点云数据进行基于狼群算法的直线拟合时，不需要再对点云数据进行处理，其已经具备很好的鲁棒性，只需重复步骤Step1～6，最后空间点云拟合直线如图9所示。

3 测量实验与结果

为实现列车车轴空间直线度测量的测量目的，搭建系统检测平台。

将实验系统中所测量数据与API Radian-50型号激光跟踪仪所测数据进行对比，该激光跟踪仪三维空间测量精度静态为10μm+5μm/m。

在测量实验中，将待检测的列车车轴平稳落至图2所述的工件支撑座上使车轴保持悬空状态，且保证整个测量过程中列车车轴无位移。激光跟踪仪测量法：采用API Radian-50型号激光跟踪仪首先对待检测的列车车轴两侧轴端面进行测量，构建激光跟踪仪的测量基准，并利用“连续点”测量法，分别对列车车轴各轴段进行测量。本文方法：将待检测车轴左侧标记端截面设置为测量0点，利用图2所述的XY移动平台，依次对列车车轴各轴段不同位置进行测量。测量数据如表1所示。

从表1可知直径的误差小于±0.1mm，同时，利用激光跟踪仪对该车轴直线度进行测量，得出结果为0.0635，运算时间为2.4s;而利用本文方法获得直线度为0.0717，运算时间为1.568s。兩者直线度误差小于0.01，且计算时间较跟踪仪减少34.67%。为使测量数据具有可比性，对其他3条列车车轴直线度进行测量，测量结果与激光跟踪仪测量数据对比，本文方法测量结果依次为：0.0812、0.0795、0.0788;激光跟踪仪测量结果依次为：0.0882、0.0841、0.0755。两者直线度误差均小于0.01。

4 结语

本文根据列车车轴检测精度的要求，提出了基于狼群算法的列车车轴空间直线度测量方法。首先，介绍了列车车轴空间直线度测量系统的组成结构和该系统的工作原理;然后，利用线结构光传感器对列车车轴截面进行数据采集，并对采集数据利用BP网络进行滤波、去噪处理;接着，推理了空间平面与空间球相切的空间圆拟合算法，并利用RANSAC算法迭代出符合列车车轴截面拟合的最佳点集; 最后，分析了狼群算法在空间直线拟合中的应用， 利用本文算法求得数据与激光跟踪仪数据进行对比，从而完成列车车轴空间直线度的检测。

实验结果表明：基于狼群算法的列车车轴空间直线度测量精度为0.01mm，能够满足列车车轴空间直线度测量的要求。

参考文献（References）

[1] 李晓静. 高速转向架车轴强度分析[J]. 时代农机， 2017， 44（8）： 115-115. （LI X J. Strength analysis of high speed bogie axle [J]. Times Agricultural Machinery， 2017， 44（8）： 115-115.）

[2] 李一男， 王泽. 基于Labview的小尺寸零件直线度误差检测方法的研究[J]. 科技视界， 2015（2）： 25-26. （LI Y N， WANG Z. Research on measurement method of straightness error of small size parts based on Labview[J]. Science & Technology Vision， 2015（2）： 25-26.）

[3] 余晓芬， 王鹏， 裴立明， 等. 大尺寸长轴二维直线度测量方法研究[J]. 中国机械工程， 2013， 24（14）： 1901-1905. （YU X F， WANG P， PEI L M， et al. Research on method of two-dimensional straightness measurement for long axle[J]. China Mechanical Engineering， 2013， 24（14）： 1901-1905.）

[4] 冉成荣. 动车车轴的线结构光测量方法研究[D]. 天津： 中国民航大学， 2015：52-54. （RAN C R. Research of structure light measurement method in axle of EMU[D]. Tianjin： Civil Aviation University of China， 2015：52-54.）

[5] 邱德超， 鲁铁定， 毛文飞， 等. 空间直线拟合的PEIV模型的构建与解法[J]. 大地测量与地球动力学， 2018， 38（10）： 1058-1062. （QIU D C， LU T D， MAO W F， et al. Model and solution of PEIV model for spatial straight line fitting[J]. Journal of Geodesy and Geodynamics， 2018， 38（10）： 1058-1062.）

[6] 袁周， 余晓流. 火车车轴轴径测量检测装置设计与研究[J]. 机械工程师， 2016（2）： 85-88. （YUAN Z， YU X L. Design and research on diameter measuring device of the train axle[J]. Mechanical Engineer， 2016（2）： 85-88.）

[7] 吴呼玲. 基于蒙特卡罗法与GUM法的直线度测量不确定度评定[J]. 工具技术， 2017， 51（5）： 104-107. （WU H L. Straightness measurement uncertainty evaluation based on Monte Carlo method and GUM method[J]. Tool Engineering， 2017， 51（5）： 104-107.）

[8] 陈君宝， 王宸， 王生怀. 基于变步长天牛须搜索算法的空间直线度误差评定[J]. 工具技术， 2018， 52（8）： 136-138. （CHEN J B， WANG C， WANG S H. Research on evaluation method of spatial straightness for variable step beetle antennae search algorithm[J]. Tool Engineering， 2018， 52（8）： 136-138.）

[9] 李亮， 吴侃， 刘虎， 等. 地面三维激光扫描地形测量数据粗差剔除算法及实现[J]. 测绘科学， 2010， 35（3）： 187-189. （LI L， WU K， LIU H， et al. Gross error elimination of terrain survey data obtained by terrestrial 3D laser scanning system[J]. Science of Surveying and Mapping， 2010， 35（3）： 187-189.）

[10] 吳汉洲， 宋卫东， 徐敬青. 基于多项式拟合的扩展卡尔曼滤波算法[J]. 计算机应用， 2016， 36（5）： 1455-1457. （WU H Z， SONG W D， XU J Q. Extended Kalman filtering algorithm based on polynomial fitting[J]. Journal of Computer Applications， 2016， 36（5）： 1455-1457.）

[11] 周航， 叶俊勇. 运用聚类方法的分层采样粒子滤波算法[J]. 计算机应用， 2013， 33（1）： 69-71. （ZHOU H， YE J Y. Stratified sampling particle filter algorithm based on clustering method[J]. Journal of Computer Applications， 2013， 33（1）： 69-71.）

[12] 王莎， 李浩， 吴铭飞， 等. 自适应坡度的LiDAR点云形态学滤波[J]. 勘察科学技术， 2017（2）： 26-29. （WANG S， LI H， WU M F， et al. LiDAR point cloud morphological filtering based on adaptive slope[J]. Site Investigation Science and Technology， 2017（2）： 26-29.）

[13] 李丽娟， 刘爽， 林雪竹， 等. 基于VB的BP神经网络点云去噪技术[C]// 2013国际工业设计研讨会暨第十八届全国工业设计学术年会论文集. 沈阳：辽宁省机械工程学会， 2013： 296-301.

（LI L J， LIU S， LIN X Z， et al. BP neural network of noise elimination technology based on VB[C]// Proceedings of the 2013 International Industrial Design Forum and the 18th National Industrial Design Scholar Conference. Shenyang： Liaoning Mechanical Engineering Society， 2013： 296-301.）

[14] 封顶浩， 张曦， 张旭， 等. 基于RANSAC的空间圆拟合算法及其在机械手运动检测中的应用[J]. 光学技术， 2016， 42（2）： 156-160. （FENG D H， ZHANG X， ZHANG X， et al. RANSAC-based spatial circle fitting algorithm and its application on motion range detection of a manipulator[J]. Optical Technique， 2016， 42（2）： 156-160.）

[15] 王敏， 童水光， 陈玉辉， 等. 一种基于Hough变换的快速圆检测算法[J]. 机械工程与自动化， 2018（1）： 152-154. （WANG M， TONG S G， CHEN Y H， et al. A quick circle detection algorithm based on Hough transformation[J]. Mechanical Engineering & Automation， 2018（1）： 152-154.）

[16] 刘晓艳， 邓重阳. 非均匀三次B样条曲线插值的Jacobi-PIA算法[J]. 计算机辅助设计与图形学学报， 2015， 27（3）： 485-491. （LIU X Y， DENG C Y. Jacobi-PIA algorithm for non-uniform cubic B-spline curve interpolation[J]. Journal of Computer-Aided Design & Computer Graphics， 2015， 27（3）： 485-491）

[17] 张晶， 黄琴， 兰红军， 等. 工程测量中空间圆的拟合方法研究[J]. 计量与测试技术， 2011， 38（9）： 31-32. （ZHANG J， HUANG Q， LAN H J， et al. Fitting method for 3D circular object in engineering surveying[J]. Metrology & Measurement Technique， 2011， 38（9）： 31-32.）

[18] 邓仕超， 高阳， 韩海媚. 改进的RANSAC圆检测算法[J]. 郑州大学学报（理学版）， 2018（1）： 77-81. （DENG S C， GAO Y， HAN H M. Improved RANSAC algorithm for circle detection[J]. Journal of Zhengzhou University （Natural Science Edition）， 2018（1）： 77-81.）

[19] 姚宜斌， 黄书华， 孔建， 等. 空间直线拟合的整体最小二乘算法[J]. 武汉大学学报（信息科学版）， 2014， 39（5）： 571-574. （YAO Y B， HUANG S H， KONG J， et al. Total least squares algorithm for fitting spatial straight lines[J]. Geomatics and Information Science of Wuhan University， 2014， 39（5）： 571-574）

[20] 郭际明， 向巍， 尹洪斌. 空间直线拟合的无迭代算法[J]. 测绘通报， 2011（2）： 24-25， 34. （GUO J M， XIANG W， YIN H B. Three-dimensional line fitting without iteration[J]. Bulletin of Surveying and Mapping， 2011（2）： 24-25， 34.）

[21] 陳建云， 魏道熙， 陈建锋. 狼群算法的研究[J]. 电脑知识与技术， 2016， 12（21）： 164-166. （CHEN J Y， WEI D X， CHEN J F. Research on algorithm of wolves[J]. Computer Knowledge & Technology， 2016， 12（21）： 164-166.）