基于深度Q网络的人群疏散机器人运动规划算法

周婉 胡学敏 史晨寅 魏洁玲 童秀迟

摘 要：针对公共场合密集人群在紧急情况下疏散的危险性和效果不理想的问题，提出一种基于深度Q网络（DQN）的人群疏散机器人的运动规划算法。首先通过在原始的社会力模型中加入人机作用力构建出人机社会力模型，从而利用机器人对行人的作用力来影响人群的运动状态;然后基于DQN设计机器人运动规划算法，将原始行人运动状态的图像输入该网络并输出机器人的运动行为，在这个过程中将设计的奖励函数反馈给网络使机器人能够在“环境行为奖励”的闭环过程中自主学习;最后经过多次迭代，机器人能够学习在不同初始位置下的最优运动策略，最大限度地提高总疏散人数。在构建的仿真环境里对算法进行训练和评估。

实验结果表明，与无机器人的人群疏散算法相比，基于DQN的人群疏散机器人运动规划算法使机器人在三种不同初始位置下将人群疏散效率分别增加了16.41%、10.69%和21.76%，说明该算法能够明显提高单位时间内人群疏散的数量，具有灵活性和有效性。

关键词：深度Q网络;人群疏散;运动规划;人机社会力模型;强化学习

中图分类号：TP391.7

文獻标志码：A

Abstract： Aiming at the danger and unsatisfactory effect of dense crowd evacuation in public places in emergency， a motion planning algorithm of robots for crowd evacuation based on Deep Q-Network （DQN） was proposed. Firstly， a human-robot social force model was constructed by adding human-robot interaction to the original social force model， so that the motion state of crowd was able to be influenced by the robot force on pedestrians. Then， a motion planning algorithm of robot was designed based on DQN. The images of the original pedestrian motion state were input into the network and the robot motion behavior was output. In this process， the designed reward function was fed back to the network to enable the robot to autonomously learn from the closed-loop process of “environment-behavior-reward”. Finally， the robot was able to learn the optimal motion strategies at different initial positions to maximize the total number of people evacuated after many iterations. The proposed algorithm was trained and evaluated in the simulated environment. Experimental results show that the proposed algorithm based on DQN increases the evacuation efficiency by 16.41%， 10.69% and 21.76% respectively at three different initial positions compared with the crowd evacuation algorithm without robot， which proves that the algorithm can significantly increase the number of people evacuated per unit time with flexibility and effectiveness.

Key words： Deep Q-Network （DQN）; crowd evacuation; motion planning; human-robot social force model; reinforcement learning

0 引言

随着城市经济建设的快速发展，大型购物中心、体育馆、影剧院等高密度人群的公共场所越来越多。当紧急突发事件发生时，逃生的人群往往会在出口处拥挤而形成堵塞，容易发生事故，存在着极大的安全隐患。传统人员安全疏散的方法有人工协助疏散和摆放静止物体协助疏散。前者极度浪费人力资源，并且对工作人员的安全造成威胁，而后者难以有效地适应变化的环境，疏散效果不理想。因此，在公共场所发生紧急突发事件时，如何快速、科学地疏散人群是公共安全领域中一个亟待解决的问题。

国内外科学研究者在人群疏散问题上进行了深入的研究并建立了多种模拟人群行为的模型，其中由Helbing等[1]提出的社会力模型（Social Force Model， SFM）大量用于研究紧急人群疏散。另一方面，随着计算机科学技术的发展，机器人越来越智能化，利用机器人疏散人群的方法也越来越多。Robinette等[2]提出机器人引导人群疏散到逃生出口;Boukas等[3]提出基于元胞自动机模型对人群疏散进行仿真，并利用仿真结果得到的反馈使移动机器人疏散人群。虽然这些利用机器人疏散人群的方法有一定的成效，但是由于实际疏散场景复杂，人群密度高，并且这些算法不具有学习能力，因而难以适应复杂的实际人群疏散场景。

在机器人疏散人群方法中，机器人的运动规划算法是核心，直接决定疏散效果的好坏。运动规划作为机器人领域的一个重点研究问题，是指在一定条件的约束下为机器人找到从初始状态到目标状态的最佳路径和运动参数。传统运动规划方法是在先验环境下，预先设定规则，机器人依据规则实现运动规划。然而当遇到动态未知的环境时，此类方法由于灵活性不强而难以适应复杂环境。近几年来，越来越多的运动规划研究者把目光集中到机器学习方面，其中文献[4]提出的深度强化学习就是运动规划领域的研究热点之一。深度强化学习是一种“试错”的学习方法，自主体随机选择并执行动作，然后基于环境状态变化所给予的反馈，以及当前环境状态再选择并执行下一个动作，通过深度强化学习算法在“动作反馈”中获取知识，增长经验。深度强化学习的开创性工作深度Q网络（Deep Q-Network， DQN）通过探索原始图像提取特征进行实时策略在视频游戏等领域有了重大突破，Mnih等[5]利用智能体在策略选择方面超越了人类的表现。随后Mnih等[6]又提出了更接近人思维方式的人智能体运动规划算法，并应用于Atari游戲，取得了惊人的效果。随着AlphaGo的成功，深度强化学习在运动规划问题上应用越来越广泛，例如用于无人车[7]、无人机和多智能体[8]等领域。同时，Giusti等[9]利用深度强化学习在机器人的导航上也取得了广泛的应用。基于深度强化学习算法的机器人在复杂未知的环境中学习速度更快、效率更高、灵活性更强，因此将深度强化学习应用于人群疏散机器人的运动规划算法是解决人群疏散难题的一个有效途径。

针对目前人群疏散机器人自主学习等问题以及深度强化学习的优点，本文提出一种基于深度Q网络的人群疏散机器人运动规划算法。该算法中，在基于人机社会力模型的前提下，机器人能够通过自身的运动影响周围人群的状态。通过Su等[10]提出的卷积神经网络（Convolutional Neural Network， CNN），提取人群疏散图像的特征;设计面向人群疏散机器人运动规划的DQN算法，通过DQN分析特征并进行运动规划，给出机器人的运动策略。在获取当前环境给予的反馈后，自动调整其运动参数，让机器人运动到最佳的状态，从而影响周围人群的运动状态，达到疏散人群的目的。本文方法既能解决公共安全领域中人群疏散的难题，又为深度强化学习算法在机器人领域的应用提供新思路。

1 机器人与人群的交互作用模型

本文采用文献[11]中提出的人机社会力模型作为机器人与人群的交互作用模型。人机社会力模型以SFM为基础。SFM是基于牛顿第二定律，将人群中的个体当成离散的质点，将人的运动轨迹看作是受到合力的作用效果，并综合考虑人群心理因素设计的行人动力学模型，能够解释行人逃生时行为的本质。SFM中行人受到的合力由以下三种组成：自驱动力、人与人之间的相互作用力、人与障碍物之间的相互作用力。人机社会力模型是在原始的SFM中加入了机器人对人的作用，利用人机之间的相互作用力来影响人群的行为，从而达到疏散人群的效果。

由于在紧急情况下疏散人群时机器人的运动分析较为复杂。文献[11]参照人与人之间的作用力来设计人机作用力的表达形式，如式（1）所示：

其中： fir为机器人对行人i的作用力，即人机作用力;rir表示人与机器人的几何中心距离;Ar和Br分别指人机作用力的作用强度和作用范围;k、κ为常量系数;nir表示机器人指向行人i的单位向量;tir为与nir正交的单位矢量。

其中：mi为行人i的质量;vi（t）为行人i的速度; fs为行人i的自驱动力; fij为行人i和j的相互作用力; fiw为行人i与障碍物之间的相互作用力。  在人机社会力模型中，机器人能够通过自身的运动来影响和改变周围行人的运动状态，从而为人群疏散提供机器人与人群的交互作用模型。

2 基于深度Q网络的机器人运动规划算法

在机器学习方法中，深度神经网络具有表达复杂环境的能力，而强化学习是解决复杂决策问题的有效手段，因此将两者结合起来能够为复杂系统的感知决策问题提供解决思路。DQN是一种经典的深度强化学习模型，是深度学习和强化学习的结合，也就是用深度神经网络框架来拟合强化学习中的Q值，可以使机器人真正自主学习一种甚至多种策略[12]。本文在人机社会力模型的基础上，针对人群疏散的问题，基于DQN模型设计面向人群疏散机器人的运动规划算法，优化机器人的运动方式，从而影响人群的运动，提高人群疏散的效率。

2.1 深度Q网络

DQN是一种结合了CNN与Q学习（Q-Learning）[13]的算法。

CNN的输入是原始图像数据（作为状态），输出是提取的特征;Q-learning通过马尔可夫决策[14]建立模型，核心为三元组：状态、动作和奖励（反馈）。智能体根据当前环境的状态来采取动作，在获得相应的奖励后，能通过试错的方法再去改进动作，使得在接下来的环境下智能体能够做出更优的动作，得到更高的奖励。

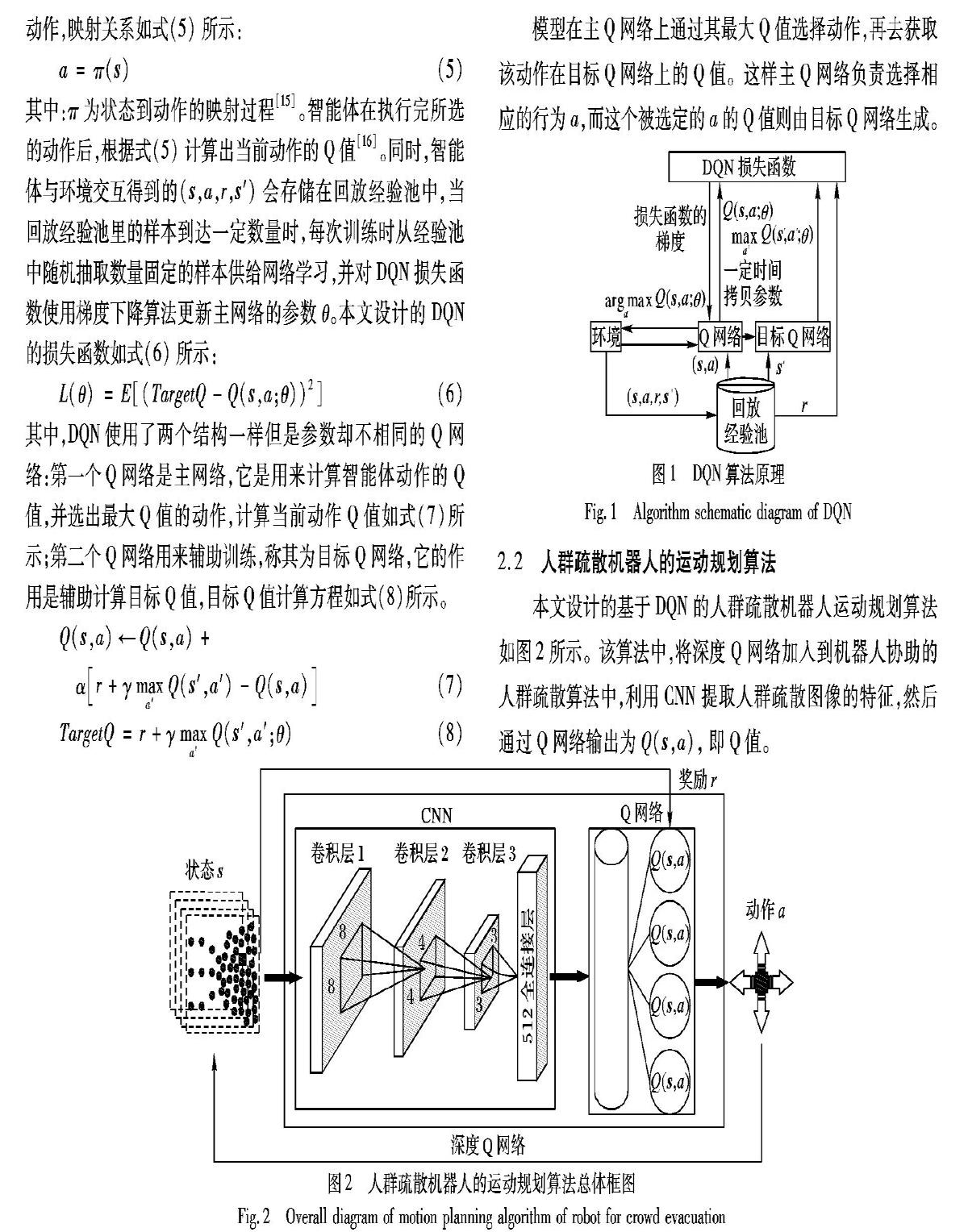
DQN用强化学习来建立模型和优化目标，用深度学习来解决状态表示或者策略表示，它从环境中获取数据，将感知的状态输入到Q网络，使机器人选择最大Q值的动作，每隔一定时间将主Q网络的参数复制给目标Q网络，并且网络会通过损失函数进行反向传播更新主网络的参数，反复训练，直至损失函数收敛，其算法流程如图1所示。

图1中：s为智能体的当前状态;s′为智能体的下一个状态;r为奖励;a为机器人的当前动作;a′为机器人的下一个动作;γ为折扣因子;θ为网络权值。智能体感知当前时刻下的状态s，根据状态与动作之间的映射关系来采取在当前环境的动作，映射关系如式（5）所示：

其中：π为状态到动作的映射过程[15]。智能体在执行完所选的动作后，根据式（5）计算出当前动作的Q值[16]。同时，智能体与环境交互得到的（s，a，r，s′）会存储在回放经验池中，当回放经验池里的样本到达一定数量时，每次训练时从经验池中随机抽取数量固定的样本供给网络学习，并对DQN损失函数使用梯度下降算法更新主网络的参数θ。本文设计的DQN的损失函数如式（6）所示：

其中，DQN使用了两个结构一样但是参数却不相同的Q网络：第一个Q网络是主网络，它是用来计算智能体动作的Q值，并选出最大Q值的动作，计算当前动作Q值如式（7）所示;第二个Q网络用来辅助训练，称其为目标Q网络，它的作用是辅助计算目标Q值，目标Q值计算方程如式（8）所示。

模型在主Q网络上通过其最大Q值选择动作，再去获取该动作在目标Q网络上的Q值。这样主Q网络负责选择相应的行为a，而这个被选定的a的Q值则由目标Q网络生成。

2.2 人群疏散机器人的运动规划算法

本文设计的基于DQN的人群疏散机器人运动规划算法如图2所示。该算法中，将深度Q网络加入到机器人协助的人群疏散算法中，利用CNN提取人群疏散图像的特征，然后通过Q网络输出为Q（s，a），即Q值。

机器人会根据当前人群疏散场景图像的状态st采取机器人协助疏散的动作at，进而根据奖励函数获得一个奖励rt，并且达到下一个状态st+1，机器人由奖励来判断该时刻自己选择的动作的好坏，并更新值函数网络参数。接着再由下一个状态得到一个奖励，循环获得奖励值，直至训练结束，得到一个较好的值函数网络。

本文设计的算法本质是机器人基于人群疏散的环境感知得到s，通过DQN选择a并且得到奖励r，从而对机器人的运动规划进行优化。因此，设计状态、动作和奖励的算法对于本文提出的运动规划算法起到至关重要的作用。

1）状态空间设计。

状态空间是机器人从环境中获取的感知信息的集合，它在DQN中是Q-Learning的主线，为Q网络提供信息数据;并且，每个输入的状态都能够前向传播，通过网络获得行动的Q值。由于原始图像尺寸过大，处理数据需要占用计算机大量的内存空间与计算资源，并且图像中还包含了许多诸如边界像素等无效的信息，因此本文只将机器人附近的区域作为状态输入图像，并对原始人群疏散图像进行缩放处理，处理后输入图像的尺寸为84×84像素。为获取前后帧的动态信息，本文对离当前时刻最近的n（本文中n=4为经验值）帧场景图像进行灰度化处理，并同时输入CNN中。因此最终输入状态的图像尺寸为84×84×4，用公式表述如（9）所示：其中：S为状态的集合;st表示当前时刻输入的状态图像;t为当前时刻 在本文设计的DQN模型中，用一个CNN来拟合Q函数，以降低深度Q网络算法复杂度。由于本文输入图像为仿真图像，图像内容较为单一，所以本文设计提取状态的CNN网络结构较为简单，如图2所示。本文设计的模型一共有4层， 其中包括3个卷积层与一个全连接层。第一层卷积运算卷积核大小为8×8，步长为4;第二层卷积运算卷积核大小为4×4，步长为2;第三层卷积运算卷积核大小为3×3，步长为1;最后经过全连接层后输出512个节点的映射集合。

2）动作空间设计。

动作空间是机器人根据自身的状态采取的行为的集合，也是实现机器人运动规划的运动参数，它在DQN中相当于指令集。本文中机器人的行为策略采用的是贪婪算法，贪婪算法是在对问题求解时，对每一步都采用最优的选择，希望产生对问题的全局最优解[17]。机器人根据设定的参数探索概率ε的大小来选择动作模式，并采取Q值最大的贪心动作。ε越大，机器人能更加迅速地探索未知情况，适应变化;ε越小，机器人则趋于稳定，有更多機会去优化策略。由于深度Q网络适用于智能体采取离散动作，而实际场景中机器人往往采用连续的动作疏散人群。但只要相邻动作间隔时间短，离散动作可近似为连续动作。机器人作为人群疏散的智能体，只有一个运动方向无法起到疏散效果;选取两个方向又具有运动范围的局限性，很难达到最优;如果选取8向运动，训练复杂度太大。因此综合考虑疏散效果和训练复杂度，本文设计的机器人的动作采取上、下、左、右4个离散动作。动作集合如式（10）所示：

3）奖励函数设计。

奖励是对机器人选择动作好坏的判断根据，奖励函数在DQN中起到引导学习的作用。DQN利用带有时间延迟的奖励构造标签，即每一个状态都有着对应的奖励。在机器人协助的人群疏散中，目的是让拥挤的人群更快速地疏散完毕，因此当前时刻撤离的人数是对机器人当前行为最直接的反馈。然而，倘若机器人在本次的动作对该次逃生出的人数有负影响，但在后几次运动中疏散人群数量较多，也不能简单判断本次机器人选择的动作是不合理的，因此本文采用机器人执行了一个动作后，未来人群在m（本文中m=5，经验值）次迭代过程中疏散的人数作为环境给予学习系统的奖励。通过逃出的人数值，可自然形成奖励值。因此本文设计的奖励函数如式（11）所示。

4）算法参数设计。

在深度强化学习算法中，参数的设计与调整对训练的效果有很大的影响。本文基于DQN的人群疏散机器人运动规划算法的参数如表1所示。

其中：学习率是指在优化算法中更新网络权重的幅度大小，学习率太高会使网络学习过程不稳定，而学习率太低又会使网络经过很长时间才会达到收敛状态。实验结果表明，学习率设为0.0001时，网络能较快地收敛到最优，因此本文选择学习率为0.0001。随机贪婪搜索中的搜索因子作为选取随机动作的概率，在观察时期，智能体是完全随机选择动作，因此本文选择初始搜索因子为1;而随着迭代次数增加，随机动作概率逐渐减小，智能体会越来越依赖于网络学习到的知识来选择动作，因此选择终止搜索因子为0.05。折扣因子表示时间的远近对预期回报的影响程度，由于在本实验中，即刻回报与未来回报同等重要，因此本文将折扣因子设为1。记忆池用来存储样本数据，在智能体学习过程中，网络会从记忆池中随机抽出一定量的批次进行训练，经尝试，本文选择记忆池大小为400000。批次大小是每一次训练神经网络送入模型的样本数，大批次可以使网络训练速度变快，但批次过大对硬件设备配置要求高，经实验，本文将批次大小设为64。目标Q为目标网络的输出，周期性的更新目标Q可以提高算法的稳定性，经实验，本文选择目标Q更新频率为1000。输入网络的图像需保证图像的清晰度并且确保囊括环境的基本特征，输入图像尺寸太大不易网络训练，输入图像尺寸太小又不易于网络提取特征，因此基于本文环境，选择输入的图像尺寸为84×84像素。

3 实验与结果分析

本文设计的人群疏散仿真环境和机器人运动规划算法均使用Python语言实现，其中DQN算法基于TensorFlow平台实现。

3.1 室内人群疏散模拟场景设计

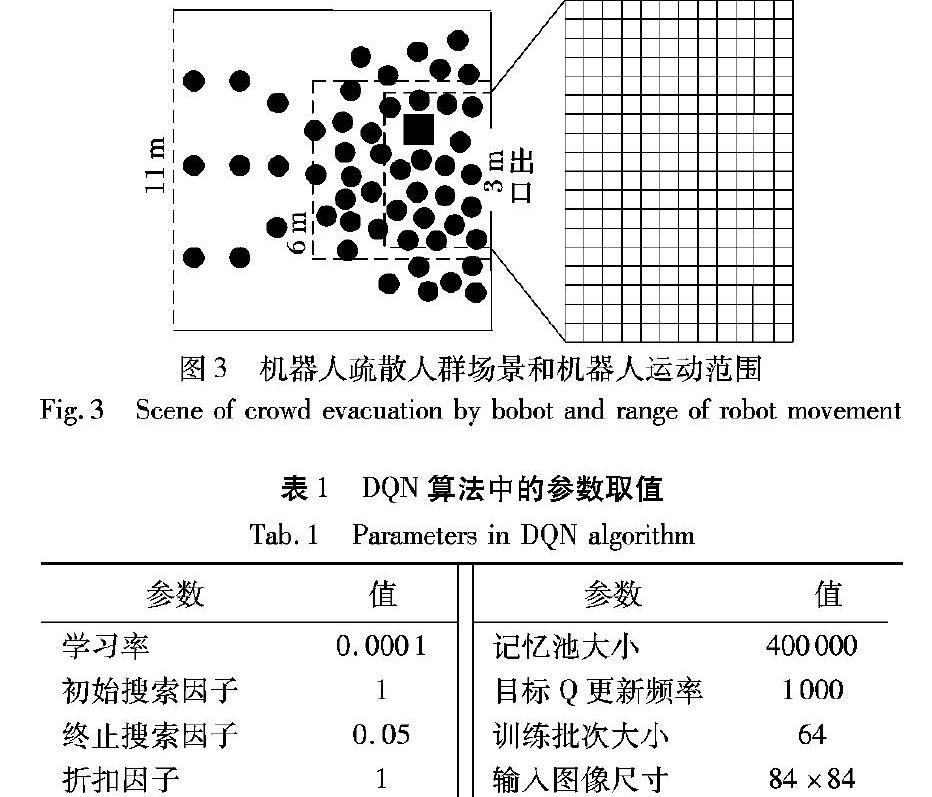
只有一个出口的室内场景，如医院、酒店的大厅等场所，是最可能发生紧急事件需要进行人群疏散的场景，因此本文设计一个矩形中带有一个出口的室内场景，并将其作为实验环境，如图3左图所示。场景大小为11m×11m，出口宽度为3m，四周外围实线方框代表墙壁，左边虚线代表行人进入通道。本文设定图3为某酒店大厅内安全通道的模拟场景，图中左侧虚线往左的部分区域发生了紧急事件，大楼内虚线左侧的人群从虚线上的三个入口进入通道，并从通道右侧的安全出口逃离危险。本文放置一个智能机器人在安全出口附近，并指定机器人的运动范围，让机器人通过深度Q网络学会最优的疏散策略。当紧急事件发生时，场景中的行人由于恐慌和从众心理会聚集在出口附近形成密度很大的群体。为逃离危险，各方向行人在自驱动力下向出口聚集，同时受到四周行人的相互作用力，使综合前向作用力很小甚至为负，导致人群向出口的移动速度很小甚至反向运动， 从而极度降低了疏散效率。

为了提高人群的运动速度，增加单位时间内的疏散总人数，本文基于人机社会力模型，在人群中加入一个机器人，让机器人在一定的范围内运动，通过机器人的运动来影响人群，提高人群疏散的效率。由于人群疏散重点区域在出口附近，且为保证输入网络的图像清晰和易于训练，因此选取出口附近的矩形区域作为观测区域，用于计算机器人的环境状态，如图3左图中6m×6m的外侧虚线框区域所示。在输入DQN时，该区域通过均匀采样得到84×84像素的图像。此外，由于人群疏散的主要区域也在出口附近，因此选择将出口附近的一个3.6m×5.4m长方形区域作为机器人的运动范围，如图3左图中内侧虚线框区域所示。为减少计算量和噪声，本文设定机器人的运动速度为0.6m/s，其状态每秒迭代2次，则每次迭代机器人移动距离为0.3m，在场景中的运动位置组成了12×18的矩形网格区域，如图3右图中的矩形网格所示。

为了验证算法的有效性，采用单位时间内疏散的人数作为实验评判标准。实验中每次人群疏散单位时间为100s，在单位时间内疏散的总人数是疏散效果及性能的直接体现;同时，直接将机器人两次迭代之间的逃生人数作为机器人一次运动的奖励rt，每一轮人群疏散实验中将每次机器人运动所得奖励（一次机器人运动疏散人数）累加，即得到本文评判疏散效果的性能参数，即总疏散人数。实验初始人数为100，初始位置在场景中随机生成，并且设定人群按照一定的间隔时间从左边进入场景。实验中每次人群疏散单位时间为100s，实验目的是最大化单位时间内疏散总人数，提高疏散效率。行人的半径设定为0.3m，用黑色实心圆表示（如图3所示），速度由初速度和其受到的综合作用力决定;行人期望速度为6m/s;

机器人的边长为1m，用黑色矩形表示，机器人在运动范围内有上、下、左、右4个动作。为减少噪声的干扰，在每一次人群疏散实验中，机器人的状态每迭代1次，行人运动状态迭代5次。此外，为保证行人源源不断进入场景，从图3中左侧三个位置每秒各产生1个水平速度为6m/s、纵向速度为0的行人，如图3所示。

3.2 静止机器人的人群疏散

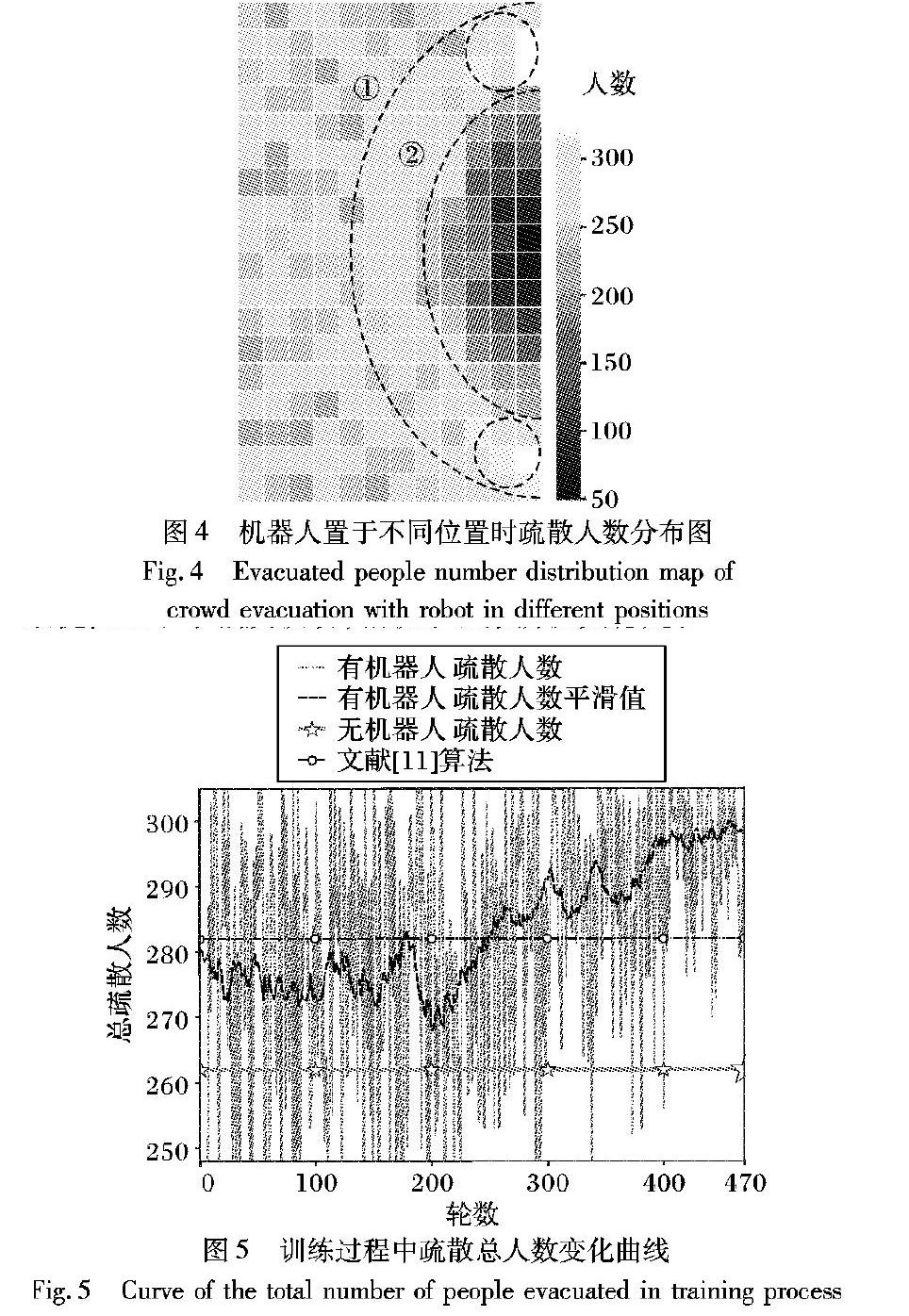
由于在人群中合理擺放静止物体对人群也有疏散作用，因此本文在训练运动机器人之前，先探讨静止不动的机器人对人群疏散的影响。为观察静止机器人处在不同位置对行人的运动，以及对固定时间内疏散总人数的影响，本文将机器人的运动范围划分成如图3右边所示的12×18的网格，并将机器人置于每个小方格所在位置，保持静止状态，测试并记录单位时间内总逃生人数;并且，将静止机器人在每个小方格位置中对应的疏散总人数映射为二维图像，以白色为背景，每个小方格颜色为由白色到黑色由疏散人数决定的离散采样，如图4所示，标尺上数字代表总疏散人数。

通过分布图可以看出将静止机器人置于不同位置时总疏散人数呈现明显的分层结构。在以出口为圆心的半圆内，越靠近出口，总疏散人数越少，即对人群疏散有负面影响。在此半圆中，水平方向单位距离疏散人数值的变化比竖直方向更大一些。较好的疏散位置处在以出口中心为圆心的带状区域内，如图4所示。当越过该带状区域后，即曲线①往左，总疏散人数没有太大的变化。疏散人数变化大的位置在带状区域靠近门的位置，如图4中曲线②所在的位置附近的区域。最优疏散位置及区域在出口附近上下两侧靠近右边墙体的位置，如图4中两个椭圆区域所示。当机器人置于此区域时，单位时间内的疏散人数最多，即机器人的最佳疏散位置。

3.3 运动机器人的人群疏散

静止机器人疏散分布图大致由疏散效果较差的门口半圆区域、较优的带状区域（包括最优的椭圆区域）、无明显变化的带状外区域组成，因此本文任意选取对这三种区域具有代表性的4个位置作为机器人初始位置集，测试本文提出的基于DQN的机器人运动规划算法，观察机器人运动轨迹。训练DQN时，每次人群疏散实验随机从4个位置中选取一个作为机器人初始位置。

在DQN中，奖励的变化是衡量模型训练是否有效的重要参数。在本文提出的人群疏散机器人运动规划算法中，奖励由疏散的人数直接决定，因此为了显示模型训练的过程，将训练过程中人群疏散的轮数与每轮实验中单位时间内疏散的人数的变化关系用曲线表示，分析本文方法的有效性，如图5所示。每轮实验的单位时间为100s，即每轮实验中，人群和机器人的初始状态记为t=0s的时刻，人群疏散实验到t=100s时结束，然后人群回到初始状态，机器人从初始位置集随机选取一个位置作为机器人的初始位置，重新开始新的一轮实验。本文模型训练时人群疏散实验总轮数为470。

训练前期处于观察阶段，机器人随机选择动作，每轮的逃生总人数相差较大。由于总体曲线波动较大，将其平滑处理，更能表现出训练效果的变化。由图5可看出，轮数小于200时的总疏散人数波动较大;训练中期处于探索阶段， 机器人通过记忆池中的数据学到越来越优化的动作序列;训练后期则是网络参数的微调阶段，此时只有小概率探索，逃生人数在最优值上下小幅度波动，相较于观察阶段更稳定。

未设置任何机器人情况下的人群疏散主要基于人与人之间的社会力模型，疏散场景与添加机器人时的场景一致。此种情况下，单位时间内（100s）疏散总人数为262人，如表2中的数据和图5中由星型标注的直线所示。

在测试阶段，为观察机器人运动规划过程，本文在三个代表性区域额外各选取一个位置作为机器人的初始位置，分别记为P1、P2和P3，测试机器人在100s内人群疏散实验中的运动过程，并记录其运动轨迹，分别作为测试实验1、测试实验2和测试实验3，其过程分别如图6所示。三次实验的总疏散人数如表2所示。为方便观察机器人的运动方式，将机器人的运动轨迹画在分布图上，并研究不同时段机器人所处的位置。此外，为验证机器人是否找到最优位置或区域，本文用虚线椭圆标记机器人最后10s的运动轨迹，如图6所示。

测试过程采用本文设计的算法，机器人运动状态每迭代1次，利用DQN的动作价值评估函数，对当前状态下的每个动作进行评估，选取价值最大的，即期望下总疏散人数最多的动作作为机器人的运动规划结果。在测试实验1（如图6（a）所示）中，机器人运动起点为P1，终点为Q1。疏散总人数达305人，与无机器人时疏散262人相比，疏散人数增加了16.41%。由于DQN算法在轨迹上的每个位置都选取当前价值最大的动作，则出现图6（a）中机器人向着最优区域运动的轨迹，同时因机器人每个动作都是所在状态下最优的，疏散人数最多的，最优动作的累加使总疏散人数最大，因此运动轨迹是起点为P1时的最优轨迹。

由于在带状外区域单位距离疏散人数值变化不大，当人群有波动时容易产生噪声，造成偶尔机器人往左运动的现象。当机器人所处状态中，疏散人数分布图的某一方向的梯度与其他方向相比越大时，DQN价值函数对此状态下最优动作的评估越准确。如测试实验2（如图6（b）所示）中的前7s运动轨迹所示，从P2开始到t=3s，左方向一直是单位距离疏散人数值增加最快的方向。从t=3s到t=7s的轨迹与图4中②虚线所框半圆相切，可看出向下是疏散人数分布图的梯度最大的方向。实验2中，机器人运动起点为P2，终点为Q2。疏散总人数达290人，与无机器人时疏散262人相比，疏散效率增加了10.69%。

在测试实验3（如图6（c）所示）中，机器人运动起点为P3，终点为Q3。开始时机器人处在带状区域大概中間位置，周围疏散人数分布图的梯度较小，加上噪声干扰，导致机器人初段运动轨迹较波折，但总方向是往下，即为人群疏散较好的位置运动。由于DQN能最大化奖励的原理，总疏散人数也被最大化了，疏散总人数达到319人，与无机器人时疏散人数相比增加了21.76%。此外，在三次实验中，机器人总会沿着梯度下降最快的路线到达最优区域及其附近区域。

为表明本文方法的有效性，除了与无机器人时对比外，还与文献[11]中采用传统的机器人运动规划人群疏散算法进行对比，因两者的行人运动都基于人机社会力模型，场景相似，具有较好的可比较性。为保证对比实验的有效性，本文选取文献[11]中的最优参数。经实验，在单位时间内（100s），传统方法疏散总人数为282人。

可明显看出本文提出的基于深度Q网络的算法在训练稳定后的疏散人数明显比传统方法多。此外，文献[11]方法需要针对每个实验场景，反复手动调整来优化人群疏散的参数，工作量大且模型难以达到最优;而本文模型能够通过DQN自主在环境中学习，寻找最优的疏散策略，灵活性更好、更具智能性，适合大多现实中的场景。

综上所述，通过本文提出的基于DQN的机器人运动规划算法，机器人能够学习在不同初始位置下的最优运动策略，最大限度地提高总疏散人数，与无机器人干预以及传统人群疏散方法相比，能够有效地提高紧急情况下疏散人群的效率。

4 结语

本文提出了一种基于深度Q网络的机器人运动规划算法，并应用于人群疏散算法中，协助完成疏散人群。此算法不仅适用于本文场景，同样也适用于与本文场景有相同特性的其他室内人群疏散的场景。该方法结合了深度学习中的CNN和强化学习中的Q-learning，通过当前时刻下环境图像到机器人运动指令的端到端的学习，改变机器人的运动状态，利用机器人与行人之间的相互作用，使机器人能够在拥挤的情况下更加灵活、有效地疏散人群。本文实验部分模拟了室内密集人群的逃生场景。结果表明，人群疏散机器人会随着训练的迭代次数增加而积累学习的经验，从而能够运动到最优位置，有效地疏散人群。由于应用DQN算法需要大量计算资源，容易产生维度灾难，本文通过源源不断产生人群使场景内人数在一定范围内波动来解决维度灾难的问题。因此，未来的工作将集中在解决固定疏散人数时深度强化学习面临的问题，使疏散效率达到更优，并且利用3D场景模拟实际的摄像机拍摄的视频来解决人群疏散的问题。

参考文献（References）

[1] HELBING D， MOLNR P. Social force model for pedestrian dynamics[J]. Physical Review E： Statistical Physics， Plasmas， Fluids & Related Interdisciplinary Topics， 1995， 51（5）： 4282-4286.

[2] ROBINETTE P， VELA P A， HOWARD A M. Information propagation applied to robot-assisted evacuation[C]// Proceedings of the 2012 IEEE International Conference on Robotics and Automation. Piscataway： IEEE， 2012： 856-861.

[3] BOUKAS E， KOSTAVELIS I， GASTERATOS A， et al. Robot guided crowd evacuation[J]. IEEE Transactions on Automation Science and Engineering， 2015， 12（2）： 739-751.

[4] POLYDOROS A S， NALPANTIDIS L. Survey of model-based reinforcement learning： applications on robots[J]. Journal of Intelligent and Robotic Systems， 2017， 86（2）： 153-173.

[5] MNIH V， KAVUKCUOGLU K， SLIVER D， et al. Human-level control through deep reinforcement learning[J]. Nature， 2015， 518（7540）： 529-533.

[6] MNIH V， KAVUKCUOGLU K， SLIVER D， et al. Play Atari with deep reinforcement learning[EB/OL]. [2018-12-10]. http：//export.arxiv.org/pdf/1312.5602.

[7] HWANG K， JIANG W， CHEN Y. Pheromone-based planning strategies in Dyna-Q learning[J]. IEEE Transactions on Industrial Informatics， 2017， 13（2）： 424-435.

[8] IMANBERDIYEV N， FU C， KAYACAN E， et al. Autonomous navigation of UAV by using real-time model-based reinforcement learning[C]// Proceedings of the 14th International Conference on Control， Automation， Robotics and Vision. Piscataway： IEEE， 2016： 1-6.

[9] GIUSTI A， GUZZI J， CIRESAN D C， et al. A machine learning approach to visual perception of forest trails for mobile robots[J]. IEEE Robotics and Automation Letters， 2016， 1（2）： 661-667.

[10] SU M C， HUANG D， CHOW C， et al. A reinforcement learning

approach to robot navigation[C]// Proceedings of the 2004 International Conference on Networking， Sensing and Control. Piscataway： IEEE， 2004： 665-669.

[11] 胡學敏， 徐珊珊， 康美玉， 等. 基于人机社会力模型的人群疏散算法[J]. 计算机应用， 2018， 38（8）： 2165-2166. （HU X M， XU S S， KANG M Y， et al. Crowd evacuation based on human-robot social force model[J]. Journal of Computer Applications， 2018， 38（8）： 2165-2166.）

[12] XIE L H， WANG S， MARKHAM A， et al. Towards monocular vision based obstacle avoidance through deep reinforcement learning[EB/OL]. [2018-12-10]. https：//arxiv.org/pdf/1706.09829.pdf.

[13] LILLICRAP T P， HUNT J J， PRITZEL A， et al. Continuous control with deep reinforcement learning[EB/OL]. [2019-01-10]. https：//arxiv.org/pdf/1509.02971.pdf.

[14] CUENCA ， OJHA U， SALT J， et al. A non-uniform multi-rate control strategy for a Markov chain driven networked control system[J]. Information Sciences， 2015， 321： 31-47.

[15] 赵玉婷， 韩宝玲， 罗庆生. 基于deep Q-network双足机器人非平整地面行走稳定性控制方法[J]. 计算机应用， 2018， 38（9）： 2459-2463. （ZHAO Y T， HAN B L， LUO Q S. Walking stability control method based on deep Q-network for biped robot on uneven ground[J]. Journal of Computer Applications， 2018， 38（9）： 2459-2463.）

[16] CHEN Y， LIU M， EVERETT M， et al. Decentralized non-communicating multiagent collision avoidance with deep reinforcement learning[C]// Proceedings of the 2007 IEEE International Conference on Robotics and Automation. Piscataway： IEEE， 2017： 285-292.

[17] CHEN D， VARSHNEY P K. A survey of void handling techniques or geographic routing in wireless network[J]. IEEE Communications Surveys and Tutorials， 2007， 9（1）： 50-67.