深圳市气温空间插值方法比较

何轮凯 孙立群 李晴岚 谢坤 王书欣 王德立 徐倩

（1 中国科学院深圳先进技术研究院，深圳 518055；2 深圳市气象局，深圳518040；3 香港大学，香港）

0 引言

气象数据作为环境因子，是地学和气候模型等相关研究的重要参数[1]。理论上气象要素的空间分布可以通过高密度站网采集，然而实际上气象观测站点的空间分布稀疏异质，观测序列长短不一，为网格化的模型应用带来了许多不确定性[2-3]。因此，利用有限的站点进行合理的空间分布插值计算不仅可以提高模型运行效率，更有助于气象预报结果的精细化显示[4]。常见的插值方法包括反距离权重插值法（Inverse Distance Weighted，简称IDW）、局部多项式插值法（Local Polynomial Interpolation，简称LPI）、克里金插值法和薄板样条函数法（Thin Plate Spline，简称TPS）等[5]。由于气象要素的变化较为复杂，不同插值方法插值得出的结果有较大的差别，不存在绝对最优的插值方法，但存在在特定环境区域中的最优插值方法[6-7]。如何根据一个区域的地形、气候变化特征、站点分布等选择最合适的气温插值方法对于气温数据进行格点化表达是一个很重要的问题。

目前，薄板样条函数法与克里金法在考虑到地形因素影响的气象数据空间插值中具有较高的准确率和效率[8]。薄板样条函数法和克里金法只将空间分布作为观测数据的函数，不需要其物理过程与先验知识，有效地提高了插值的准确度[9]。Hutchinson等[10]从理论上对比了薄板样条函数法和克里金法的不同，认为当样条函数法的粗糙度稳定，且克里金法选择了适当的半变异函数时，两者均能获得较好的插值效果，但是实际应用中数据结构更加简单、误差估算更加精确的薄板样条函数法更受推崇[11]。为了方便薄板样条函数法的使用，Hutchinson等开发了气候数据薄板样条函数法插值的专用软件Anusplin[12]，该软件可以引进与气象要素相关的协变量线性子模型，如高程等，基于不依赖于模型的广义交叉验证（GCV）法，相对于克里金法更加稳健，更能反映气象要素在空间中自然分布的特征规律，已在国际上得到广泛的应用[13-14]。

目前，深圳市共有近200个可以正常工作的自动气象观测站。在广东省乃至全国都属于自动站点较为密集地区。然而，这些站点相对于深圳近2000 km2的面积来讲仍然无法满足某些气象模式大区域、无缝隙、网格化的数据要求，并且在气象预报结果的表达上也无法做到千米级的精细化呈现。基于以上现状，选用较好的插值方法，建立深圳市气温格点化数据集十分有必要。本研究将以深圳市128个气象站点的月平均气温数据为研究对象，对包括薄板样条函数法（TPS）、反距离插值法（IDW）、局部多项式插值法（LPI）、普通克里金和协同克里金在内的5种插值法进行插值效果比较，对比各类插值方法的优劣及插值效果的影响因素，为深圳市气温插值的方法选择提供科学依据，优化插值效果。

1 数据与方法

1.1 数据来源

本研究使用的气温数据集来源于深圳市气象局，时间序列为2017年的1—12月，原始数据集共有195个站点，每个站点对应的数据集包含了2017年每天的平均气温，为保证气温插值的质量，站点中异常数据、缺失数据超过4%的站点均予以剔除。剔除有部分缺失数据、数据异常等的67个站点，剩余128个站点，由站点逐日的数据推算出每个月的平均气温后整理。每个站点数据包括站点的代号、经度、纬度、海拔和月平均气温。

由于边缘效应，本研究使用的插值范围比深圳市的实际范围略大，为113.7°—114.7°E，22.3°—22.9°N，但插值时不增加深圳市外的站点。考虑到深圳市高程图精度过高不利于计算效率的提高，精度过低插值效果不够精确，调整精度为0.02°×0.02°（约为2 km×2 km）。

1.2 插值方法

本研究使用了五种插值方法，分别是IDW、LPI、普通克里金（OK）、协同克里金（Cokriging）和基于Anusplin软件的TPS，以下分别对这五种方法进行简单的介绍。

1.2.1 反距离权重法

IDW基于地理学第一定律-相似相近[15]，假设彼此距离较近的要素要比彼此距离较远的要素更相似。当为任何未测量的位置预测值时，反距离权重法会采用预测位置周围的测量值。与距离预测位置较远的测量值相比，距离预测位置最近的测量值对预测值的影响更大。反距离权重法假定每个测量点都有一种局部影响，而这种影响会随着距离的增大而减小。由于这种方法为距离预测位置最近的点分配的权重较大，而权重却作为距离的函数而减小，因此称之为反距离权重法。该方法计算方式较为简单，但易受极值的影响。本研究使用的IDW插值法基于ArcGIS中Geostatistical Analyst模块中确定性方法提供的IDW算法进行插值计算。

1.2.2 局部多项式插值法

全局多项式插值法可以根据整个表面拟合多项式[16]，而LPI可以对位于指定重叠邻域内的多个多项式进行拟合。通过使用大小和形状、邻域数量和部分配置，可以对搜索邻域进行定义。LPI仅使用既定邻域内的点对指定阶数（0 阶、1 阶、2 阶、3 阶，等等）的多项式进行拟合。邻域相互重叠，每次预测所使用值是位于邻域中心的拟合的多项式的值。本研究使用的LPI插值法基于ArcGIS中Geostatistical Analyst模块中确定性方法提供的LPI算法进行插值计算。

1.2.3 普通克里金

普通克里金是最早被提出和系统研究的克里金法[17]，并随着地统计学的发展衍生出一系列变体和改进算法。普通克里金是一个线性估计系统，适用于任何满足各向同性假设的固有平稳随机场。各向同性假设下的固有平稳随机场中，数学期望与其位置无关，且协方差仅是点间距离的函数。通常随机场的协方差函数是未知的，需要使用变异函数作为近似，此时变异函数也仅与点间距离有关。本研究使用的普通克里金插值法基于ArcGIS中Geostatistical Analyst模块中地统计方法提供的Kriging算法进行插值计算。

1.2.4 协同克里金

协同克里金是在普通克里金的基础上发展起来的一种插值方法[18]，其将与变量高度相关的辅助信息作为协变量加入到克里金插值过程中，既考虑自变量的空间自相关性，又考虑了协变量与自变量之间的相关性。该方法建立于协同区域化变量理论的基础上，通过建立变异函数模型和趋势移除，利用主变量自相关性和主变量与其他所有变量的互相关性进行更好的预测。本研究使用的协同克里金插值法基于ArcGIS中Geostatistical Analyst模块中地统计方法提供的Cokriging算法进行插值计算。

1.2.5 薄板样条函数

薄板样条函数插值法最早由Wahba[19]于1979年提出，1984年Hutchinson等对其进行了改进，以适用于更大的数据集[10]。Bates等将其拓展为局部薄板光滑样条法[20]。薄板样条函数法在插值过程中利用一个平面去拟合所有的站点，使得它可以通过站点组成的样条，得到逼近所有控制点且曲率最小的光滑曲面。光滑参数由GCV的最小化或广义最大似然的最小化确定，使用了最优的光滑参数实现了逼真度和光滑度的最佳平衡，保证精度可靠且曲面光滑连续[21]。本研究中使用GCV的最小化确定光滑参数，评估误差后使用优化较好的二次样条函数进行插值研究。本研究使用的薄板样条函数插值法基于Anusplin4.3版本的算法。

1.3 检验方法

本研究采用交叉验证法中的留一验证法对5种插值方法的精度进行评价，每次使用气象站点中的一个站点作为验证资料，剩余的站点用作训练资料，进行插值处理，通过测算实际值与预测值的误差评价不同方法的插值精度。采用平均绝对误差（MAE）和均方根误差（RMSE）作为5种插值方法误差的评价指标，直接评价插值方法得出的结果与实际温度的温度差值：

式中，Z0(xi)和Z(xi)分别是第i个站点的预测值与实际值。平均绝对误差与均方根误差越小，说明插值方法的准确度越高。

基于反距离权重法、局部多项式法、普通克里金法、协同克里金法等4种方法，利用ArcGIS中Geostatistical Analyst模块提供的交叉验证方法，使用所有数据对趋势和自相关模型进行估计。它会每次移除一个数据位置，然后预测关联的数据值。在本研究中，交叉验证每次会省略一个点，然后使用剩余的127个点计算此位置的值。将省略点位置的预测值与实际值相比较。然后对第二个点重复此过程，以此类推。交叉验证会对所有点的测量值和预测值进行比较。

基于Anusplin自带的薄板样条函数法，对每个月的数据集进行分割，每次生成一个数据量为127个点的子集，以及剩余1个点的验证集，将子集输入Anusplin软件的插值模块生成插值表面，使用Anusplin带有的验证功能输入验证集，得到验证集中的点对应的预测值，重复此过程128次，可得到所有数据点的验证结果。

2 结果与分析

2.1 空间分布对比

基于图1 中深圳市气象站点分布与高程图，以2017年7月为例，应用TPS、IDW、LPI、OK、Cokriging等5种方法进行平均气温的插值（图2）。与IDW、LPI、OK等相比，将高程作为协变量进行插值的TPS与Cokriging法得出的插值结果更加平滑。TPS法插值得出的温度分布为22.34～29.51 ℃，Cokriging法插值得出的温度分布为21.96～30.63 ℃，两者结果相近。对其他月份的插值结果均绘图显示，结果表明，Cokriging和TPS插值的结果更加平滑，而精确度有待进一步评估，以下阐述五种插值方法的误差检验

图1 深圳市气象站点分布（a）与高程图（b） Fig. 1 Distribution of meteorological stations (a) and elevation map in Shenzhen (b)

2.2 逐月对比

之后交叉验证得到的MAE与RMSE作为判断标准，判断每个月份五种方法插值的精度高低。如图3显示，IDW法在10月时RMSE最大，为0.90 ℃，且MAE最大，为0.49 ℃。3月时RMSE与MAE最小，分别为0.67和0.36 ℃。LPI法的RMSE与MAE分别于10和9月达到峰值，为0.87和0.47 ℃。3月时LPI插值法的RMSE和MAE最小，为0.65和0.35 ℃。OK法的RMSE与MAE在10月达到最大，分别为0.90和0.49 ℃。3月时RMSE与MAE较小，分别为0.66和0.37 ℃。加入了高程作为协变量的Cokriging法的RMSE和MAE在10月达到最大，分别为0.83和0.56 ℃，3月时RMSE与MAE较小，为0.68和0.37 ℃。与IDW、LPI、OK、Cokriging法相比，TPS法的RMSE与MAE明显较小，在9月达到峰值，分别为0.37和0.29 ℃，3月时RMSE与MAE较小，分别为0.25和0.18 ℃。在1—12月中每个月TPS法的MAE与RMSE均远小于其余四种方法。

图2 基于5种插值方法的深圳市7月平均气温空间分布 （a）OK法插值结果；（b）LPI法插值结果；（c）IDW法插值结果；（d）Cokriging法插值结果；（e）TPS法插值结果 Fig. 2 Spatial distribution of July mean temperature in Shenzhen based on five interpolation methods(a) Interpolation results of OK; (b) Interpolation results of LPI; (c) Interpolation results of IDW; (d) Interpolation results of Cokriging; (e) Interpolation results of TPS

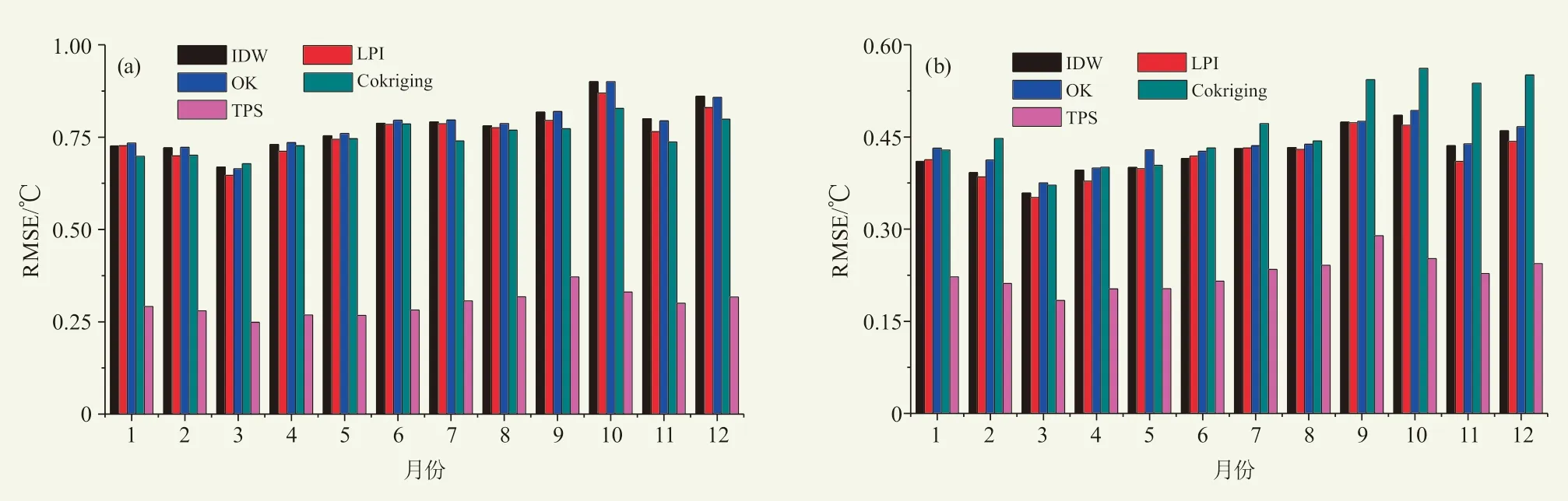
图3 基于5种插值方法交叉验证误差的RMSE、MAE逐月分析 Fig. 3 Monthly analysis of RMSE and MAE based on cross-validation errors of five interpolation methods

在插值精度上，RMSE与MAE的变化具有季节特征，在3月左右的插值精度明显优于10月左右的插值精度。RMSE结果显示，TPS插值法在春夏季节的插值精度优于秋冬季节。从误差范围来看，冬季的插值结果在负误差方向表现比其他时间尺度明显，表明利用Anusplin对研究区冬季气温数据插值时，会更大概率出现低估的情况[22-23]。某些地区由于局地气候的影响，在季节气温方面表现出特殊性，如在冬季这些地区的站点气温远高于同海拔区域[24]。本研究也发现，9月—次年2月的某些站点气温高于同海拔地区，导致Anusplin估算气温时出现低估的现象。这可能是夏季气温插值误差小于冬季的原因。此外，不同站点下垫面性质的不同，对气温插值的结果也有一定影响，会造成一定的误差。

大气层的主要直接热源是地面，离地面越远，得到的地面辐射越少，气温也就越低。根据气温垂直递减率[21]，每上升100 m，气温下降0.6 ℃，将高程作为协变量加入插值模型中，可以更好地模拟地形对气温的影响。

以深圳市最高峰梧桐山及周边的站点为例（图1中红框内的5个站点，5个站点的信息如表1所示），大梧桐及小梧桐站点地势较高，沙头角、莲塘、明珠等站点地势较低，高程图显示，该地区地形变化较大，其中小梧桐站点介于最高峰和平原之间，是地形变化最明显的站点。将该站移除，以剩余站点的数据进行插值，得到小梧桐站点的插值结果（图4）。该站点的插值结果显示，在12个月的气温逐月插值中基于Anusplin软件的TPS方法准确度明显优于其余方法。IDW、LPI、OK结果基本一致，偏高3～4 ℃。Cokriging方法结果误差稍小，TPS方法的插值结果与实际观测结果基本一致，平均每月的误差为0.27 ℃。

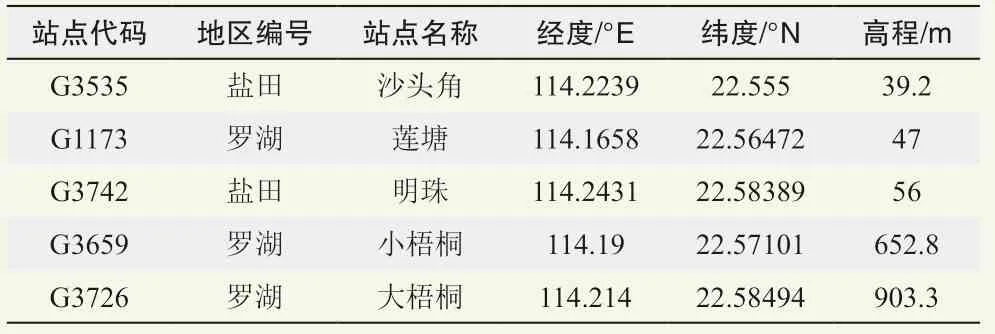
表1 梧桐山及周边站点信息 Table 1 Information of Wutong Mountain and its surrounding sites

2.3 影响因素分析

高程可能影响插值的最终结果，将每次插值的误差绝对值（即观测值减去预测值再取绝对值）与深圳市高程图进行对比，发现分布特征与海拔有一定的联系。对每个月的插值误差绝对值与该观测点的海拔进行Pearson相关分析（图5），结果显示，IDW、LPI、OK的插值误差绝对值与海拔之间的相关系数较高，12个月的相关系数均大于0.75，呈现显著正相关关系。Cokriging将高程作为协变量进行插值，一定程度上避免了高程对误差的影响，因此Cokriging方法的误差与高程相关性较小。TPS方法的插值误差与高程相关性较小，可基本认为TPS方法可最大程度减少由高程带来的温度插值误差。

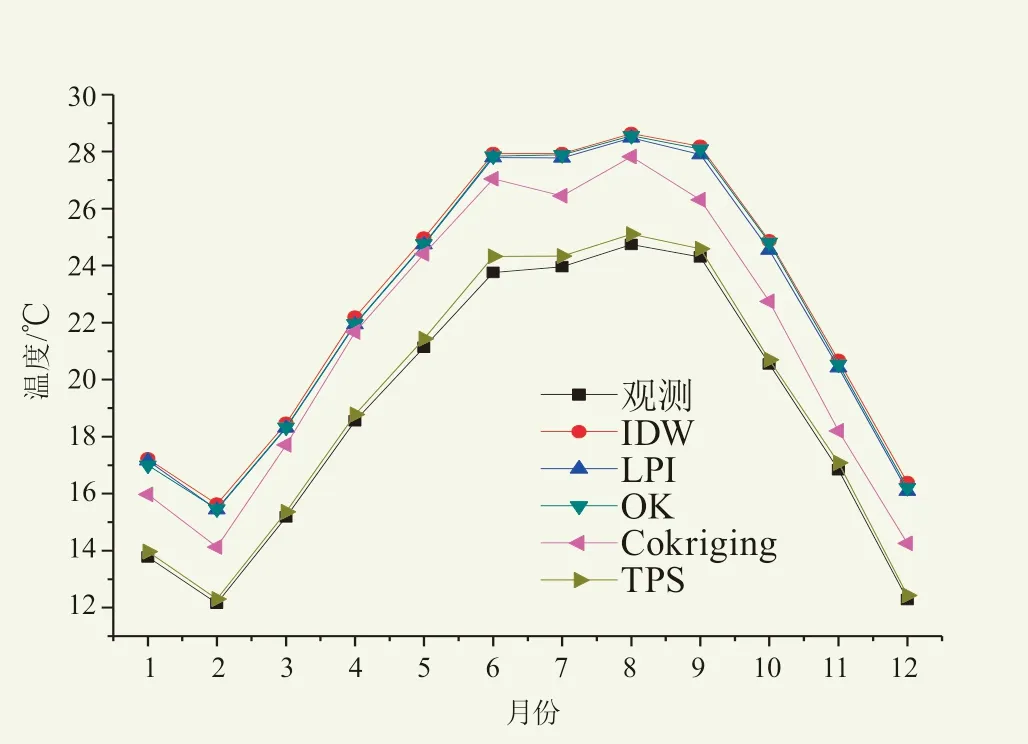
图4 不同插值方法对小梧桐站气温插值结果逐月分析 Fig. 4 Monthly analysis of temperature interpolation results at Xiaowutong station by different interpolation methods

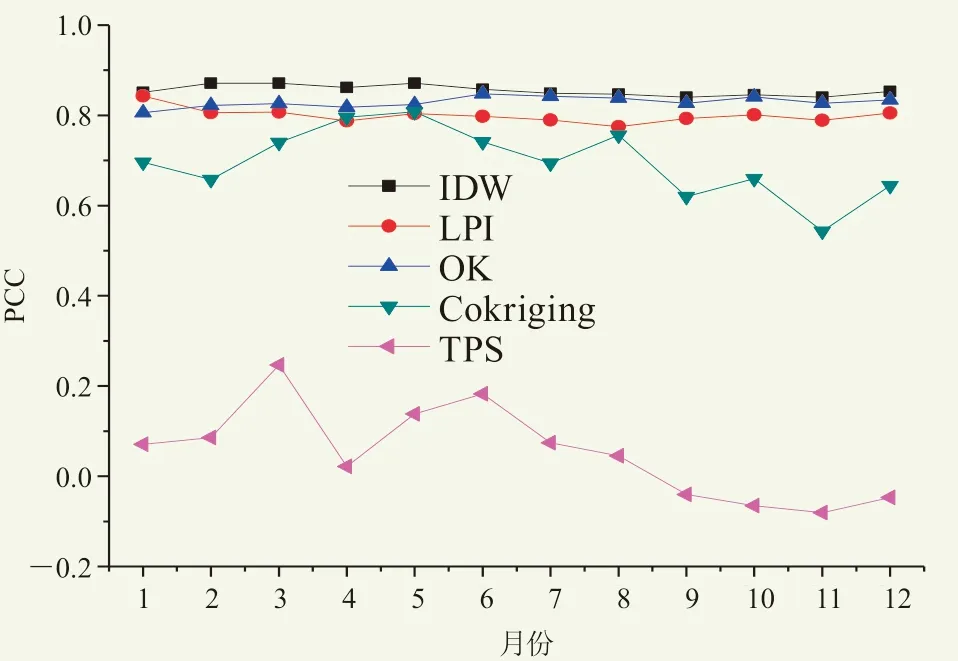
图5 5种插值方法交叉验证结果误差绝对值与高程相关性分析 Fig. 5 Analysis of absolute error and elevation correlation of five interpolation methods for cross-validation results

3 结论

基于2017年深圳市128个气象站点的气温监测数据与深圳市数字高程模型，对比了反距离权重法、局部多项式插值法、普通克里金法、协同克里金法和Anusplin软件中的薄板样条函数法，对深圳市2017年全市月平均气温进行了空间插值，通过气象站点逐个交叉验证的方法，对比了不同空间插值方法在不同月份的插值结果。研究显示：

1）与IDW、LPI、OK法相比，Cokriging法与基于Anusplin软件的TPS法插值得到的拟合曲面均较为平滑。

2）在插值交叉验证结果的逐月对比中，与IDW、LPI、OK、Cokriging法相比，TPS法的均方根误差与平均绝对误差较小，可有效提高气温数据的空间插值的精度。2017年深圳市气温空间插值的交叉验证误差显现明显的季节性特征，TPS法的春夏两季精度明显高于秋冬两季。

3）高程是IDW、LPI、OK法插值重要的误差来源，其他方法插值与协变量为高程的TPS法的主要差别在于不考虑高程所带来的系统误差。TPS法在气温插值上的应用充分考虑到了海拔的影响，因此避免了高程带来的误差，Anusplin软件在气温空间插值领域值得推荐。