基于S函数三相异步电机复合故障特征研究
2019-11-15何水龙沈徐红蒋占四
何水龙,沈徐红,蒋占四
(桂林电子科技大学 机电工程学院,广西 桂林 541004)
0 引 言
由于构造简单、运行和拖动性能可靠,三相异步电机被广泛应用于工农业生产中,但因其负载多变和工作环境恶劣,致其故障频发,从而引起停机、停产等事故,造成巨大的经济损失。目前,电机常见故障分为机械故障(轴承故障、转子不对中、转轴弯曲等)和电气故障(定子、转子绕组短路故障等),其中由于绝缘材料受到环境和机械应力影响而老化引起的定子绕组匝间短路故障高达38%;由于电机制造、安装、过载运行、污染和不正确的润滑等因素导致的轴承故障约为30%。
众多研究者在定子绕组匝间短路和轴承故障单一故障建模和诊断方面做了许多研究,也取得了一系列的成果。如,文献[1-2]通过Simplorer与电磁仿真软件的联合仿真,研究了电机在定子绕组匝间短路故障下的输出电流以及电磁转矩等特性。文献[3-5]采用多元仿真手段,建立电机正常状态和定子绕组匝间短路的故障模型,并用于单馈异步运行时的电机故障特性分析。文献[6]分析由于滚动轴承故障引起的扭矩波动,得到定子电流中产生的故障频率成分,并采用定子电流分析方法,实现无传感器诊断技术。文献[7]以定子电流分析方法为基础,模拟轴承故障状态下定子电流的变化情况,利用变分模态分解对采集到的故障定子电流信号进行分析,从分解的电流信号中提取轴承的故障特征信息。实际上感应电机存在电磁耦合现象,导致机械故障和电气故障互相影响,最后形成两种故障并存的机电故障耦合情况。考虑电机轴承故障实物实验验证的经济和时间成本,对故障电机进行建模分析结合理论研究,可实现电机在多种工况下性能的精准分析,提高效率、降低成本[8],并获取特征。
基于上述思路,本文通过多回路理论建立通用感应电机本体模型正常状态与定子匝间短路故障状态的数学方程。利用Simulink中具有强描述动态系统能力及独特输入输出特性的S-函数进行方程编写;以特定轴承外圈故障引起的周期性波动扭矩与额定转矩相互叠加作为机械故障动态输入,耦合本体模型中定子绕组匝间短路故障完成电机复合故障仿真模型。重点分析了额定转矩下复合故障时电机定子电流幅值谱、频谱、包络谱等时域、频域特性,并对电流故障特征进行电磁转矩和转速辅助验证分析。
1 三相异步电动机故障模型
1.1 三相异步电动机定子绕组匝间短路故障数学模型
图1中异步电机发生匝间短路故障位置在定子A相绕组,故障将A相分成未短路的匝数(As1)和已短路的匝数(As2)。短路后形成闭合回路的绕组As2视为定子的一相新绕组。因此故障后的电机近似为一个多相异步电机,具有四相定子绕组和三相转子绕组。假定绝缘破损部分的电阻Rf忽略不计,设短路绕组系数μ=As2/(As1+As2)。

图1 三相异步电动机定子A相短路结构
(1)建立定子绕组匝间短路故障在两相静止坐标系中的数学模型状态方程:
电流量作为状态变量,电压方程和磁链方程化成标准的状态方程形式。为得到这种形式,要对磁链方程中的电感矩阵求逆,但当电机正常状态运行时μ=0,该电感矩阵是非奇异阵。而用μif作状态变量代替短路电流if,如此电感矩阵在任何短路系数下均为奇异阵,形成通用的电机正常状态与定子绕组匝间短路故障状态方程。
由于多数绝缘材料的绝缘破损位置电阻为0,所以短路回路的电压uf可视为0。
状态方程为
(1)
其中,状态量、输入量和输出量分别为
x=[isαisβirαirβμif]T,u=[usαusβ0 0 0]T,y=[isαisβirαirβ]T为能清晰表达,定义:

式中,Lls,Llr为定、转子绕组漏感;ωr为电动机转子的角速度。
简化状态方程系数矩阵得:
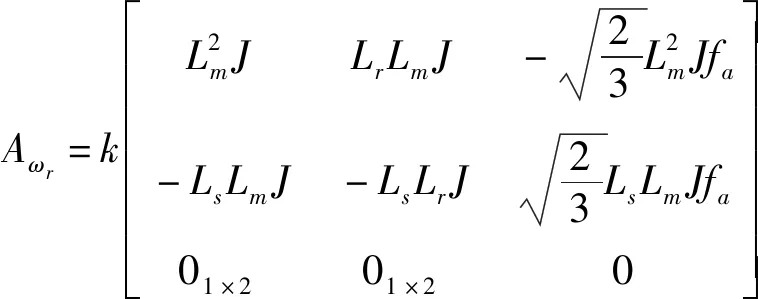

(2)转矩方程
(2)
(3)运动方程
(3)
式中,J为旋转机组的转动惯量;p为电动机极对数;Te,TL分别为电动机的电磁转矩、负载转矩。
(4)坐标转换公式
为保证转换前后磁势与功率不变,三相静止坐标系和两相静止坐标系之间的转换公式为
(4)
其中,
(5)
式中,θ,θr为坐标系旋转角度、转子电角度。
1.2 S-函数
S函数是一种动态系统的计算机描述语言,采用特定的调用语法,与Simulink的系统模块描述不同。S函数接收来自Simulink求解器的相关信息,并响应求解器发出的命令,与Simulink系统模块与求解器的交互作用相似。S函数具有模块化、可重载、可封装、面向对象编程及可视化等特点,提高了系统仿真的效率和可靠性,尤其是可实现复杂的动态系统跟数学描述,利用此方法建立的模块简单且具有较高的可移植性,在仿真过程中可对仿真对象进行精确控制,能很好地模拟全数字化控制系统,提高仿真精度。
S函数的完整结构体系包括输入部分、状态部分和输出部分。其中,输出是采样时间、输入和块状态的函数,Simulink块的数学关系如图2所示。

图2 S函数的输入输出关系
Simulink模型的仿真过程在初始化阶段需完成一些参数的设置,包括系统的输入输出个数、状态初值、采样时间和所需调用的方法等;在调用执行阶段,Simulink仿真引擎通过调用仿真方法进行计算输出、更新离散状态和计算连续状态等,该阶段需要反复调用执行,直到仿真结束。
基于电机定子绕组匝间短路故障数学模型,在sfuntmpl.m模板中输入程序代码,然后在Simulink中建立复合故障的子模块,即匝间短路故障模型。
1.3 滚动轴承外圈故障模型
本文选择电机连接负载的输出端滚动轴承的外圈故障为研究对象建立机械故障模型。根据Trajin对轴承单点损伤实验验证,轴承故障引起的转子中心径向偏移程度十分有限,主要还是反映在转矩的振动情况中,故以扭转变化为出发点实现建模。需对轴承相关的振动转矩幅值、脉冲宽度、方波脉宽比进行计算。
根据Hertz的两个弹性球体碰撞力计算公式,即两球之间的最大挤压力为
(6)
其中,
式中,m1,m2为两球质量;V0为碰撞时两球的相对速度;r1,r2为两球的半径;μi,λi为第i个球的剪切模量、泊松比。
根据图3所示,钢球以保持架旋转速度Vc前进,则钢球通过宽度为 的外圈缺陷时的碰撞速度V0为
(7)
式中,d为滚珠直径;b为外圈缺陷宽度;Vc为保持架旋转速度。
(8)
式中,D为滚动轴承的节圆直径;α为轴承的接触角;fr为轴的转频。
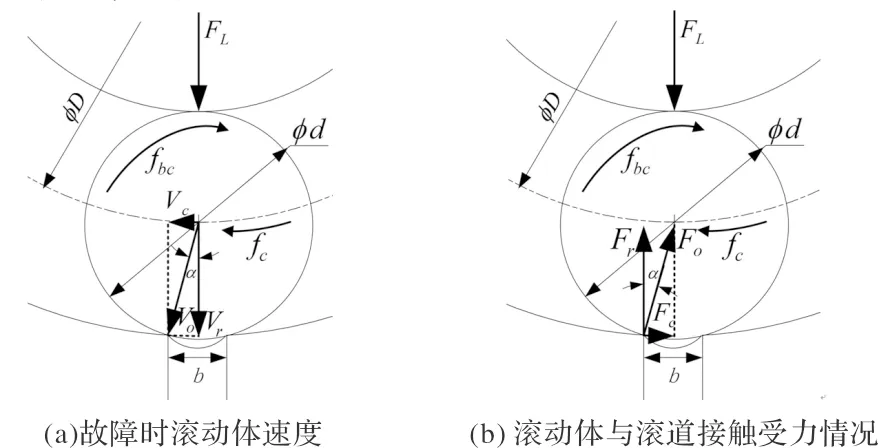
图3 考虑运动学时滚动轴承外圈故障力学模型
由于滚珠和外圈都为钢,故υ1=υ2=1/3,μ1=μ2=8.1×105kg/cm2,计算得:
本文采用的轴承型号为6307,主要参数如表1所示。

表1 滚动轴承基本参数
由表得出,r1=6.745mm;r2=(d+D)/2=36.027mm;m1=1.023×10-5kg·s2/cm;m2=1.97×10-4kg·s2/cm;将上述参数代入式(6)得:
n=1.221 069×106,mr=1.02827×105。
设缺陷宽度b=8mm,轴承内圈旋转频率fr=23.33 Hz,转子转速ωr=146.61 rad/s,则:
根据式(6),与V0方向相反的最大冲击反作用力F0=1969.4N。
由此产生的周向力矩Tc为
(9)
轴承旋转时实际发生碰撞的长度是b/2,需
(10)
故障时,滚动体与故障点接触瞬间Mc最大,并在Δt时间内降为0,该下降过程缓变,假设Mc在Δt时刻后才变为0,即Mc为一个脉冲函数,脉冲宽度为Δt,脉冲间隔为滚动体通过外圈的频率fo。
(11)
则该周期为1/fo=0.0139s,这样可以计算出方波的脉宽比约为35%。
综上得出与轴承相关的转矩振动幅值Tc=34.20N·m、脉冲宽度Δt=0.0048s、方波脉宽比35%,用于周期性脉冲转矩以模拟轴承故障模型。
基于轴承故障数学模型,对稳定额定转矩叠加一个脉冲方波表示附加的周期性转矩,在Simulink中建立复合故障子模块,即轴承外圈故障模型。
2 仿真实验
2.1 仿真模型
在仿真模型中,设定仿真三相异步电机参数如下:
PN=3kW,UN=220VAC,nN=1400r/min,p=2,Rs=1.9188Ω,Ls=0.24122H,Rr=2.5712Ω,Lr=0.24122H,Lm=0.234H,J=0.0052kg·m2,TLN=20.46N·m。
使用前面所述复合故障的两个子模型将负载转矩作为输入,为电机模型添加具有周期性振动特征的负载,模拟轴承外圈损伤故障,并将两模型联立实现机电联合仿真,完整模型如图4所示。
仿真模型中短路系数为一阶跃波形,设定t=0~5s,短路系数μ=0;t=5~10s,μ=0.01,即定子绕组匝间短路故障的程度为0.01。此外,t=0~2s转矩阶跃波形为0,表示电机的空载运行过程;t=2~10s,阶跃至20.46N·m表示额定负载转矩过程,通过开关实现轴承正常运行到电机处于额定转矩时轴承外圈故障的瞬态变化过程。

图4 基于S函数的三相异步电动机复合故障模型
整个仿真过程中,定子绕组接入频率为50 Hz的额定电压,转子绕组短路。
2.2 定子电流信号分析
图5、图6和图7分别为电机在正常、轴承外圈故障、定子匝间短路、复合故障4种情况下的定子电流信号、定子电流频谱以及包络谱。
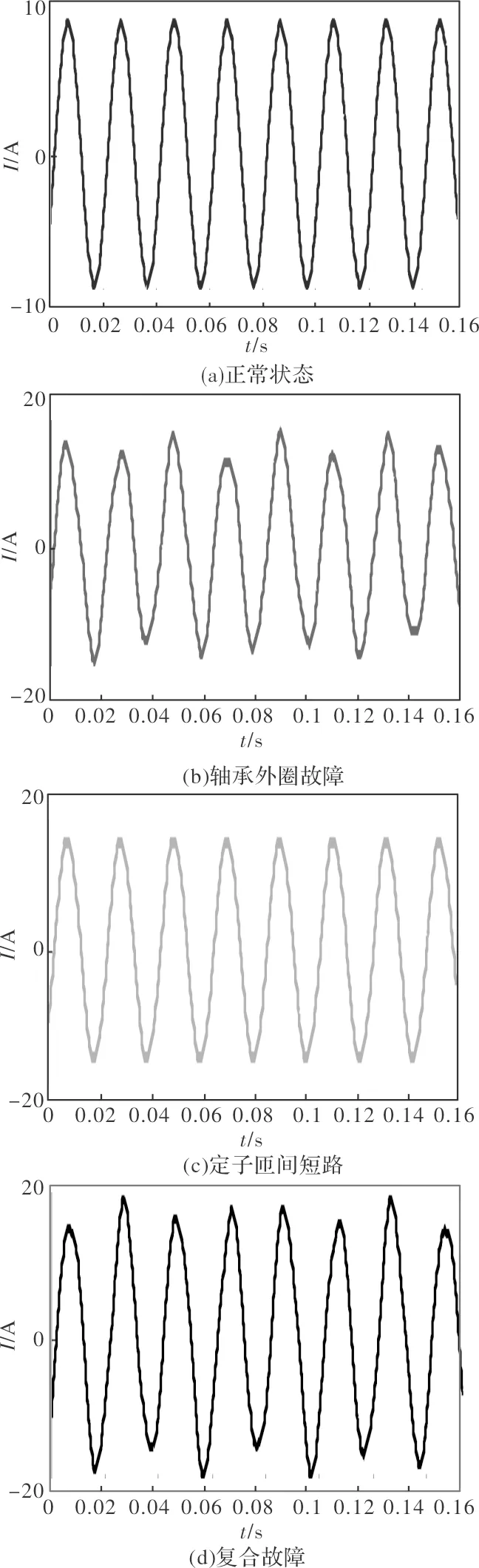
图5 电机正常与故障条件下定子电流信号


图6 电机正常与故障条件下定子电流频谱对比


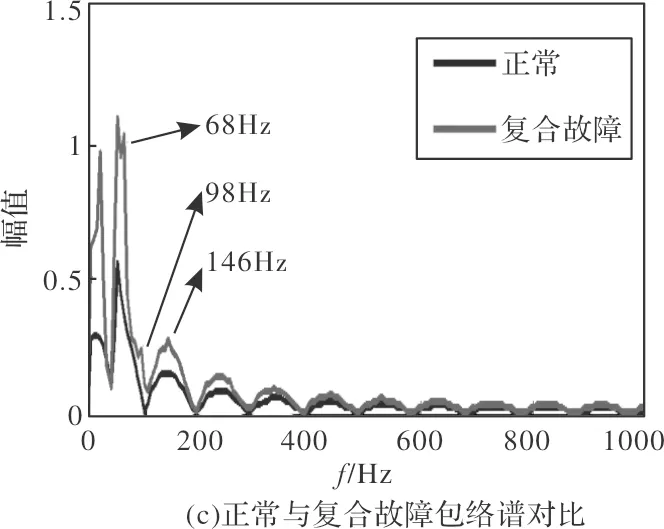
图7 电机正常与故障条件下定子电流包络谱对比

2.3 转速波动信号分析
图8和图9分别为电机在正常、轴承外圈故障、定子绕组匝间短路、复合故障4种情况下的转速波动信号、转速波动频谱。


图8 电机正常与故障条件下转速波动信号

图9 电机正常与故障条件下转速波动频谱对比
从图8可见,与正常情况相比,各种故障状态在转速波动信号上均有所体现。轴承外圈故障引起的额外周期性脉冲方波转矩波动Tc导致了如图8(b)所示电机转速的周期性三角波,使转速瞬时降低。图8(c)定子绕组匝间短路使转速信号形成以降低转速的周期性的正弦信号波动。图8(d)中复合故障转速波动信号与单一故障的周期性波动不同,复合故障没有导致转速的明显的周期性波动,表现出混叠的信号,难以从时域波形中得到正确故障信息。
通过对比正常电机频谱与3种故障状态下电机频谱,图9(a)出现了由于轴承外圈故障导致的转速波动引起的频率成分73.32Hz、146.6Hz,与电信号包络谱中解调出的特征频率73Hz、140Hz相对应;图9(b)中由定子绕组匝间短路故障导致的转速波动引起的频率成分97.76Hz,与电信号包络谱中解调出的特征频率98Hz相对应;图9(c)中复合故障与正常状态的频谱对比得,复合故障导致的频率分量73.32Hz、97.76Hz、140.5Hz,与从电信号包络谱中解调出的68Hz、98Hz、146Hz等频率分量相对应。因此进一步验证电流信号包络谱出现的特征频率。
2.4 电磁转矩信号分析
图10、图11和图12分别为电机在正常、轴承外圈故障、定子绕组匝间短路、复合故障4种情况下的电磁转矩信号、电磁转矩频谱以及包络谱。
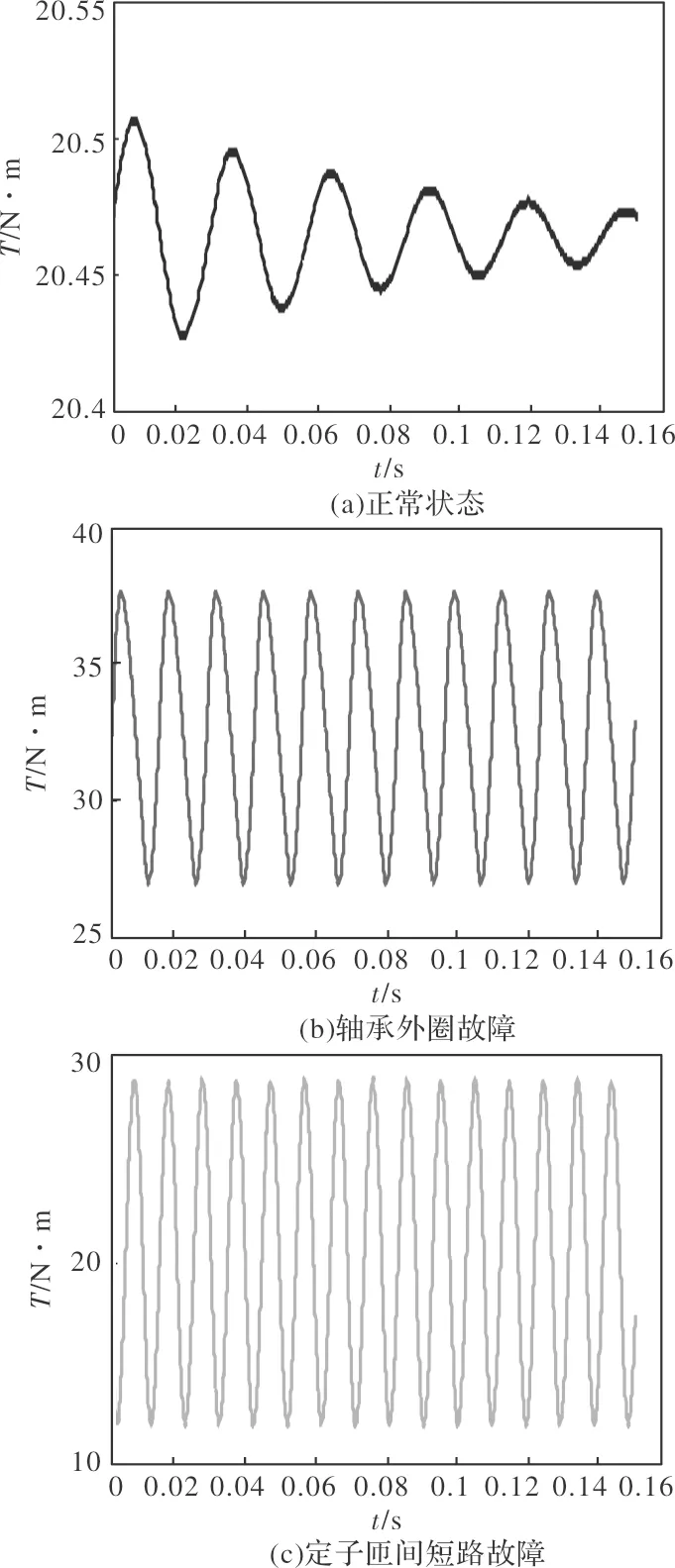

图10 电机正常与故障条件下电磁转矩信号
从图10可见早期故障后的电机电磁转矩幅值比正常电机信号幅值都有波动,其中轴承外圈故障使信号整体超过正常信号幅值,并形成周期信号;定子匝间短路故障导致信号在正常电机信号幅值处上下周期性波动,但平均电磁转矩值与正常状态时相近;复合故障时呈现的电磁转矩波形混叠了轴承外圈故障信号与定子匝间短路信号,电磁转矩平均值增大,伴有不稳定波动性。

图11 电机正常与故障条件下电磁转矩频谱对比
为得到故障引起电磁转矩波动更准确的故障频率分量信息,对电磁转矩进行包络分析。图12(a)表现为与图11(a)相同的频率成分;图12(b)中出现偶次工频4fs=200Hz附近的特征频率201.60Hz,使定子匝间短路在电磁转矩信号中的特征频率成分更明显;图12(c)中复合故障包络谱除聚集了两种单一故障的特征频率外,还出现了与信号频谱相同的其他频率分量30.55Hz、171.10Hz。因此与转速信号同时验证电流信号特征频率用于诊断的可行性。
对时域波形进行频谱分析与包络谱分析,进一步得到故障特征分量。通过对比正常电机频谱与三种故障状态下电机频谱,图11(a)出现了由轴承外圈故障导致的电磁转矩波动引起的,与转速频谱频率成分相同,同时与电流信号包络谱中解调出的特征频率73Hz、140Hz相对应频率成分73.32Hz、146.60Hz;图11(b)中因为定子绕组匝间短路故障导致的电磁转矩波动引起的频率成分97.76Hz,与转速频谱频率成分相同,且与电流信号包络谱中解调出的特征频率98Hz相对应;从复合故障与正常状态的频谱对比可见,由复合故障导致的频率分量73.32Hz、97.76Hz、140.5Hz,与转速频谱频率成分相同,且与从电流信号包络谱中解调出的68Hz、98Hz、146Hz等频率分量相对应,此外还出现了其他频率分量30.55Hz、171.10Hz等比单一故障特征频率简单叠加更多的频率分量。

图12 电机正常与故障条件下电磁转矩包络谱对比
3 结 论
本文基于多回路数学理论和轴承周期性振动特性分析建立了三相异步电机定子绕组匝间短路故障和轴承故障的机电复合故障模型,并对复合故障的定子电流、转速及电磁转矩进行分析和仿真研究,结果表明,电机复合故障模型能够准确反映故障发生时电机实际运行状态过程表现的电流、转速、电磁转矩等信号特性,验证了基于S函数的混合机电联合仿真方法的准确性和可行性,为工程技术人员进行复合故障仿真提供了依据。同时,经过转速信号频谱、电磁转矩频谱与包络谱对定子电流频谱、包络谱进行分析表明,定子电流信号富含故障特征信息,可对电机复合故障进行综合判断,为该类复合故障在工程实际中的检测诊断提供技术手段。
