考虑初始状态的均质非饱和土入渗过程解析解
2019-11-15
(1.山东电力工程咨询院有限公司,山东 济南 250100; 2.山东黄河勘测设计研究院,山东 济南 250013; 3.山东正元建设有限责任公司,山东 济南 250100)
研究降雨条件下的非饱和土渗流过程对许多岩土工程或环境岩土工程的实践有重要意义,例如,自然或人工边坡稳定性分析[1-4]、矿床或城市垃圾填埋场设施的覆盖层设计[5-6]、涉及膨胀土和湿陷性土的工程问题[7-8],等等。解决这些问题的关键和难点在于计算降雨入渗过程在非饱和土体中引起的渗流场[9]。
Richards方程是描述非饱和土体中瞬态渗流的控制方程。针对该方程的求解,以往的研究多采用数值模拟手段给出数值解[10-12],而解析方法的研究相对较少。实际上,与数值解相比,解析解更清晰简洁,能更直观地显示定解问题对边界条件的响应,且便于对各影响因素进行参数敏感性分析,并能对数值解的结果进行验证[13]。Srivastava 等推导了均质、非均质土体降雨条件的一维瞬态入渗解析解[14],基于此模型,詹良通[13]和李宁[9]等人分别推导了考虑坡度影响和降雨形式的渗流解析解。Chen 等[15-16]提出了非稳恒降雨条件下的入渗解析模型。Huang等[17]和Ghotbi等[18]也分别基于Fourier积分变换和同伦分析方法(HAM)提出了降雨入渗过程的解析解。在初始状态的处理方面,上述研究或将存在前期降雨并达到稳态入渗时刻作为初始条件[9,13-14,16],或假定初始含水率(水头)分布为线性或特定函数[15,17-18],而根据实际情况,初始状态是可以选择在任意时刻,相应含水率(水头)分布往往是不规则的。诚如Zhan 等[19]所述,前期降雨所形成的初始状态对水头分布的影响甚至大于后续降雨。朱伟等指出在非稳定渗流中,能不能正确地考虑初始水分量将会对计算结果产生非常大的影响[20]。在采用的数学算法方面,前人多借鉴Ozisik (1980)关于偏微分方程的解法[21],在解析表达式中存在复杂的积分变换项[9,15-17]。该类方法在理论上是先进的,但数学算法稍显复杂,不利于直接应用。因此,需要进一步研究任意初始状态的入渗过程解析解,并考量初始状态的影响。
本文采用指数函数描述非饱和土体的土水特征曲线及其渗透系数随水头的变化,对任意初始状态的非饱和土入渗过程解析解进行了推导。最后基于所推导模型,分析初始状态对含水率分布的影响。
1 理论推导
1.1 基本假设
(1) 土体为均质,非饱和渗流由基质吸力差(水头差)决定,不考虑溶质吸力的影响。
(2) 不考虑非饱和土的回滞特性。
(3) 地下水位始终稳定,不受土表降雨入渗过程的影响。
(4) 降雨过程雨强稳定,即为均匀降雨。
1.2 控制方程
Richards为非线性偏微分方程,目前它已衍生出3种基本格式,即压力水头格式(h-form)、混合格式(mixed form)和体积含水率格式(θ-form),其中混合格式被证实具有严格遵守质量守恒的特性,可表示为
(1)
式中,h为孔隙水压力水头;θ为体积含水率;k为渗透系数;t为时间;z为纵坐标,正方向向下(如图1所示)。
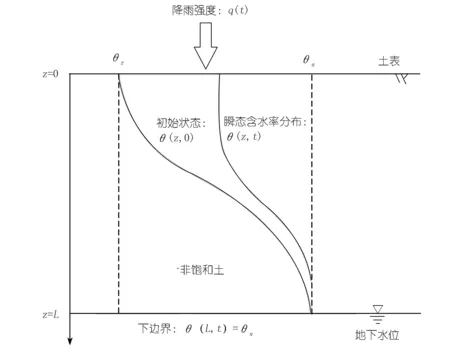
图1 入渗过程示意Fig.1 Schematic illustration of infiltration process
Yanful和Mousavi[22]指出,在非饱和土渗流中相较于大的的压力水头差,式(1)中的重力项可以忽略。同时,忽略重力项可以极大简化推导过程,避免解析解中复杂的积分或级数项[23]。因此,Richards公式可以简化为
(2)
参照文献中常用的指数函数形式[13-17,24],土水特征曲线和渗透系数方程可描述为
θ(h)=θr+(θs-θr)eαh
(3a)
k(h)=kseαh
(3b)
式中,θs和θr分别为饱和和残余体积含水率;ks为饱和渗透系数;α为减饱和系数。将式(3)代入式(2)可得
(4)
为了简便计算,定义土的扩散系数D和无量纲的体积含水率Θ分别为
(5a)
Θ=(θ-θr)/(θs-θr)
(5b)
将式(3a)、(5a)和(5b)代入式(4),并进一步化简,可得:
(6)
1.3 入渗过程解析解
降雨强度与土体饱和渗透系数的相互关系会对入渗过程产生影响。对于降雨强度小于饱和渗透系数的情况,即q≤ks,降雨将全部入渗,土表不会形成积水,也即整个过程均处于定流量入渗阶段。而对于降雨强度大于饱和渗透系数的情况,即q>ks,其起始为定流量入渗阶段,降雨一段时间后,表层土体达到饱和,降雨不能完全入渗,土表存在积水,定流量入渗阶段转化为土表积水阶段。
1.3.1定流量入渗阶段
在定流量入渗阶段,上边界为恒定的流量边界,也即降雨强度。此时的初始和边界条件可表示为
Θ(z,t)|z=L=1
(7a)
(7b)
Θ(z,t)|t=0=f(z)
(7c)
式中,L为地下水位深度;q为降雨强度;f(z)为任意初始状态含水率分布函数。式(7a)表示在地下水位处,下边界土体始终饱和,Θ始终为1;式(7b)表示上边界为恒定流量边界条件;式(7c)表示初始状态。
首先求稳态入渗时的含水率分布,设为w(z),则w(z)满足:
(8a)
w(z)|z=L=1
(8b)
-D(θs-θr)w′(z)|z=0=q
(8c)
联立式(8)可以求得w(z)的表达式为
(9)
由于原问题的边界条件为非齐次(如式(7)),因此为方便求解,引入一变量使其齐次化,令:
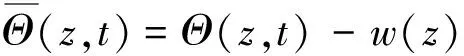
(10)
将式(9)和式(10)代入式(6)和式(7),可得:
(11a)
(11b)
(11c)
(11d)
这里,式(11a)为控制方程,式(11b)和式(11c)为边界条件,式(11d)为初始条件。根据附录中的推导过程,式(11)的解可以写为
(12)
由于式(12)中存在积分项,较难定量求得。为简便应用,用一个二次函数来拟合初始含水率分布,以消除积分变量,简化计算。由于z=L时,Θ始终为1,因此令:
(13)
式中,a和b为拟合参数。将式(9)和式(13)代入式(12),并进一步化简,可得定流量入渗阶段土体含水率瞬态分布的解析解表达式:
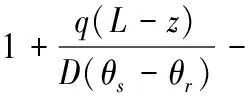
(14)
1.3.2土表积水阶段
对于q>ks的情况,假设土表积水开始时间为tp。不考虑积水造成的土表水头堆积的影响,则当t>tp时,上边界条件为恒定含水率边界条件。
首先对于积水时刻tp,可令式(14)等于1求得。设此时的含水率分布为p(z),则p(z)的表达式为
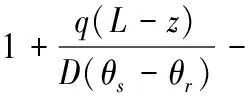
(15)
当t>tp时,定义一个新的时间变量T=t-tp,将T代入式(6)可得:
(16)
在土表积水阶段,初始和边界条件可以表示为
Θ(z,T)|z=L=1
(17a)
Θ(z,T)|z=0=1
(17b)
Θ(z,T)|T=0=p(z)
(17c)
根据Carslaw和Jaeger(1959)[25]的解法,式(16)在边界条件式(17)下的解为
(18)
由于式(18)含p(z)函数未解积分项,若直接将式(15)代入求解,算法复杂,且不能得到其解析表达式,限制其直接应用。因此,我们用二次函数来代替式(15),以实现简化。因为当T=0时,在z=0和z=L处,Θ=1,所以二次函数的表达式可写为
(19)
其中,c为拟合参数,利用式(19)拟合式(15)来可以求得其值。将式(19)代入式(18)可求得存在土表积水阶段的含水率分布解析解:
(20)
2 算例分析和讨论
本文针对降雨强度和饱和渗透系数的关系,分别进行如下两个算例讨论。如表1所示,在算例1中降雨强度q小于饱和渗透系数ks;而在算例2中,q大于ks。对算例1和算例2,均进行两种初始条件(线性和非线性含水率分布)的分析。

表1 边界条件和土性参数Tab.1 The boundary conditions and soil properties
图2为降雨强度小于饱和渗透系数时,不同时刻土体内含水率的分布,其值均由式(14)计算得出。图2(a)中,a和b分别赋值0和1来拟合线性初始含水率分布,而图2(b)中,a和b分别为2和-1.5。比较图2(a)和(b),不难发现初始状态对含水率分布产生非常大的影响。另外,图2(b)的初始状态可认为存在较强的前期降雨,由于后期降雨强度小于饱和渗透系数,土体内部渗流较快,使得表层土体含水率在t=5 h小于初始含水率。
图3展示了降雨强度大于饱和渗透系数时,不同时刻土体内含水率的分布。其初始状态设定与图2情况相同。对图3(a)和(b),其积水时刻tp分别为9.69 h和9.39 h,土表边界在t
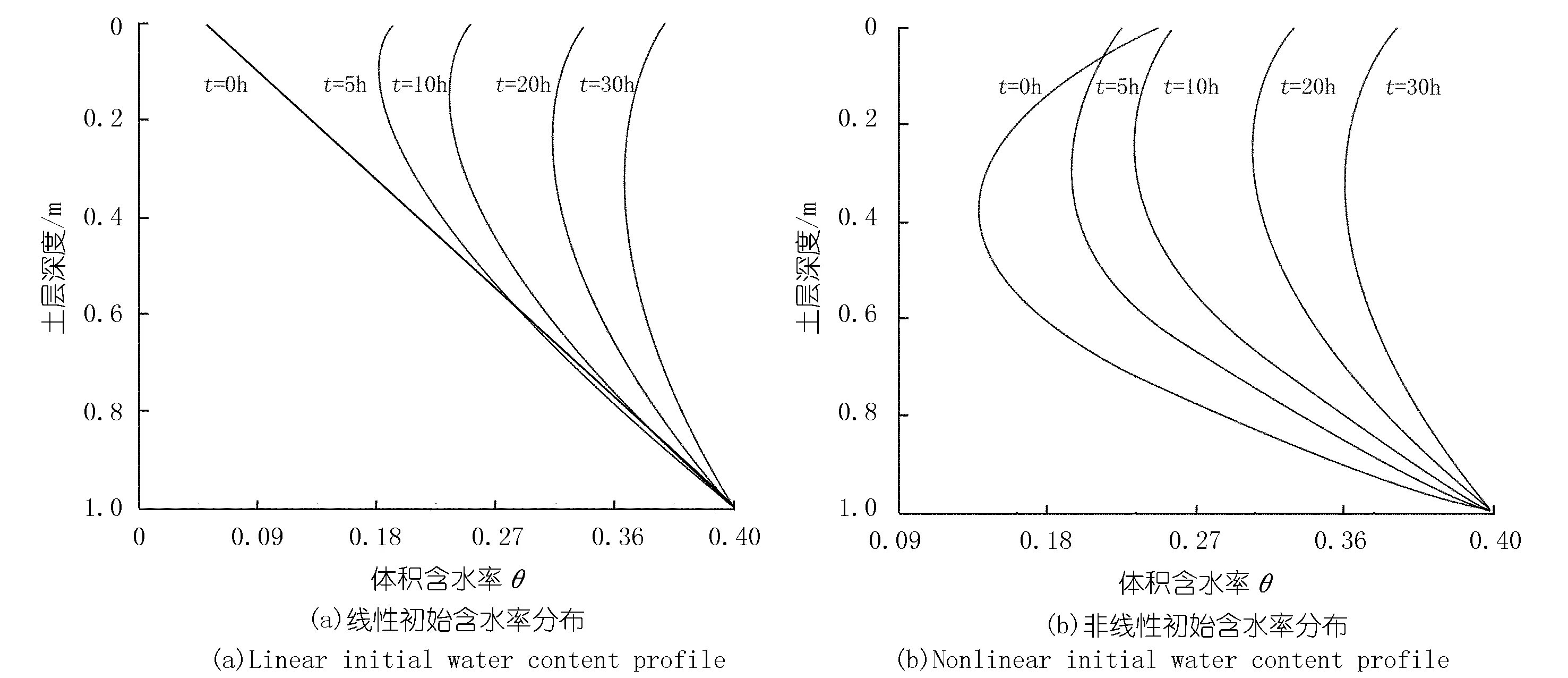
图2 算例1中不同时刻土体内含水率分布Fig.2 Water content redistribution during infiltration for Case 1
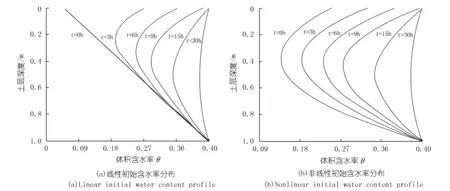
图3 算例2中不同时刻土体含水率分布Fig.3 Water content redistribution during infiltration for Case 2
情况,式(20)中的拟合参数c分别为1.53和1.68。随着时间推移,含水率分布的变化幅度逐渐变小,并最后趋于稳态。由图3可见,初始条件不仅影响含水率的大小,而且影响含水率分布形态。
3 结 论
(1) 基于指数函数来描述土水特征曲线和渗透系数随水头的变化,得到降雨强度大于或小于饱和渗透系数的入渗过程解析解。该模型可以考虑任意初始状态,并且避免了复杂的数学算法表达,无需借助编程来实现数学计算,易于应用。计算结果表明初始状态对入渗过程的计算结果有显著影响。
(2) 提出的模型能够揭示特定情况下的入渗过程机理,形式简单,能克服数值模拟的复杂数学算法及计算收敛问题,便于考察入渗过程的机理。
(3) 但同时需要考虑到,解析解的得出是基于一定的假设和简化。实际应用中,应将解析解手段和数值模拟方法结合应用。
