基于MI-PCA与BP神经网络的石羊河流域中长期径流预报

丁公博，农振学，王 超，宋培兵，雷晓辉

(1.中国地质大学(北京) 水资源与环境学院，北京 100083；2.中国能源建设集团广西电力设计研究院有限公司，南宁 530007； 3.中国水利水电科学研究院，北京 100038；4.浙江大学建筑工程学院，杭州 310058)

0 引 言

流域中长期径流预测是流域水量分配和水量调度的基础，如何构建能够准确描述流域水文特性的中长期径流预测模型并精确预测未来中长期径流是实现流域水资源管理精细化首先要突破的问题。近年来，国内外研究学者对中长期径流预报进行了大量研究，其研究重点主要集中在2个方面：一是预报模型研究。常用模型有传统统计法和现代统计法，其中传统统计法包括时间序列法[1]等方法、现代统计法则包括支持向量机法[2]、人工神经网络法[3]、半监督迭代模糊聚类法[4]、小波分析法[5]、混沌理论法[6]、灰色系统法[7]和最优预测组合法[8]等方法。其中，人工神经网络法，以其简易的网络结构，高效的运算机制和强大的知识表示能力，已被广泛应用至中长期水文预报中。为验证人工神经网络模型在水文预报中的适用性，胡军华[9]等将该方法应用于塔里木河。结果表明，率定期和检验期预报结果的合格率皆满足相关标准规范的要求。杨旭[10]，王鹏[11]等通过改进人工神经网络模型的参数和结构等，使人工神经网络模型的预测精度得到了显著提高。如何从诸多水文和气象因素中选择适合特定研究区域的预测因子是提高预测模型预测精度的关键之一。在预报因子方面，随着对水文过程物理机理认识的不断加深，预报因子的分类从之前单纯的前期降水和径流，发展到现在包括海面温度和大气环流因子等多种类型。而预报因子筛选方法也由以前的线性相关性分析法[12]等发展为现在的互信息法[13]、主成分分析法[14]等方法。Sharma[15]引入互信息(MI)的概念来描述中长期降雨预报中变量间的非线性关系。该方法在多变量时间序列自回归模型和多变量阈值时间序列自回归模型的变量识别方面取得了巨大的成功。赵铜铁钢[16]等利用互信息方法分析了长江上下游和主要干支流流量间的相关性，研究了长江主要干支流的日径流预报。结果表明，引用互信息筛选预测因子可有效提高人工神经网络模型的预报精度。虽然互信息可更好的反应预测因子与预测径流间的复杂非线性关系，但预测因子间存在信息重叠，很容易产生预测模型的“过拟合”现象，从而影响模型的预测精度；主成分分析由于能有效地解决因子冗杂、信息重叠等问题，被广泛运用于水文预报中。在赣江流域[17]、三峡水库[18]的实例研究表明，运用主成分分析方法筛选预报因子，能够缓解预报因子间信息重叠导致的“过拟合”问题，可以提高人工神经网络模型在率定期和检验期的预测精度。主成分分析虽然能够提取预报因子的主要信息部分，但是大多停留在线性相关分析上，不足以揭示径流形成的复杂变化机理。因此，为解决石羊河流域中长期径流预报的实际工程问题，考虑运用在中长期径流预报中应用广泛、效果较好的BP神经网络作为预报模型，考虑到互信息法和主成分分析法在筛选预测因子方面的优势，提出了一种耦合互信息法(MI)和主成分分析方法(PCA)的预报因子筛选方法(MI-PCA)，并以石羊河流域西营水库的入库径流预报为实例开展研究，论证所提方法的有效性。

1 模型原理和方法

1.1 互信息法

互信息法(Mutual Information，MI)是一种对多个变量(2个及2个以上)计算和呈现这些变量之间互信息的方法。变量的互信息量与相关性则呈正比关系，随着互信息量的增大或减小，相关性也会增大或减小。

当x和y2个随机变量相互独立时，其联合分布密度等于2者的边缘分布密度之积，即：

Px,y(x,y)=Px(x)Py(y)

(1)

当变量x和y具有N个观测值且为离散型随机变量时，变量间的互信息方程如下：

(2)

当变量x、y是连续随机变量时，变量之间的互信息方程如下：

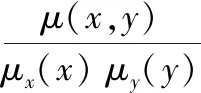
(3)

式中：μ(x,y)表示连续随机变量x和y的联合分布密度；μx(x)、μy(y)分别表示连续随机变量x和y的边缘分布密度。

当随机变量x、y相互独立时：

则MI=0。

当x、y不相互独立时，MI将趋近正无穷大。因变量的互信息值与相关性为正比关系，故随着互信息值的增大，相关性也增大。

1.2 主成分分析法

主成分分析法(Principal Component Analysis，PCA)是一种多变量统计方法，用于计算多个变量之间的相关性并导出一些主成分。在导出的少数几个主分量中都包含有原始变量的大部分信息且每个主分量中的信息彼此不相关，从而达到简化数据和降维的目的。

设初始变量和主分量分别是x1,x2,…,xp和z1,z2,…,zm(m≤p)，则各主成分计算公式如下式：

(4)

式中：z1,z2,…,zm为x1,x2,…,xP所对应的m个主成分，其中，zi与zj(i≠j)相互无关，z1为x1,x2,…,xp的线性组合且在所有线性组合中方差最大，z2为与z1不相关的x1,x2,…,xp的线性组合且在所有线性组合中方差最大，依次类推；所有的系数l可构成荷载矩阵L。

1.3 互信息和主成分分析法

互信息和主成分分析法(Mutual Information-Principal Component Analysis，MI-PCA)是结合互信息和主成分分析法2种算法的优点层级筛选预报因子的方法。其原理是在互信息选出备选因子的基础上，再计算主成分。该方法既考虑到了2变量(或多变量)之间的线性和非线性关系，又可以舍去变量间重叠部分的信息，减少了原始变量的数量，并且更突出地显示变量与研究对象间的相关性。基于互信息和主成分分析的中长期径流预报模型相比于互信息和主成分分析2种方法预报效果更好，模型稳定性更高。

1.4 BP神经网络模型原理

BP神经网络[19](Back Propagation Neural Network)是1986年由Rumelhart和McCelland为首的科学家小组提出，它是一个多层的前馈型神经网络。其模型拓扑结构包括输入层(Input Layer)、隐含层(Hide Layer)和输出层(Output Layer)，如图1所示。BP神经网络可以根据预测误差连续调整网络各层的权重，从而达到预测输出无限接近预期输出的效果。由于BP人工神经网络具有3层(3层以上)结构，对线性和非线性具有很强的映射能力，因此被广泛用于中长期水文预报领域。

图1 BP人工神经网络结构概化图Fig.1 BP artificial neural network structure generalization diagram

2 模型应用

2.1 研究区概况

石羊河流域全长250 km，总面积4.16 万km2。近年来，随着石羊河流域枯水期水资源供需矛盾的加剧，开展流域水资源优化调度及合理分配，成为解决该问题的有效途径之一。而流域水资源优化调度最重要的一个环节是中长期径流预报，预报精度将直接影响流域水资源调度的效果。因此，在分析流域特征、水文特性以及调度工程情况的基础上，研究适合流域特性的中长期径流预报方法，提高中长期径流预报的精度是石羊河流域水资源调度实施中必须首先解决的关键问题。西营水库是石羊河流域中一座控制性水利工程，兼顾流域灌溉、防洪和发电等综合利用需求。其灌溉面积达2.522 万hm2，总库容为2 350 万m3，入库径流资料相对完整且资料序列较长。因此，本研究以西营水库为例，收集西营水库1970-2016年的年均径流资料，分别构建基于MI、PCA和MI-PCA的BP神经网络模型进行预报，根据预报结果优选最适合石羊河流域的预报模型。

2.2 径流特性分析

选取西营水库1970-2016年47 a的长系列年径流数据作为预测数据。经计算，西营水库入库径流年际极值比和全年径流量变差系数均较小，分别为2.05和 0.17，表明西营水库入库径流的年际变化较小。径流的变化过程如图2所示。

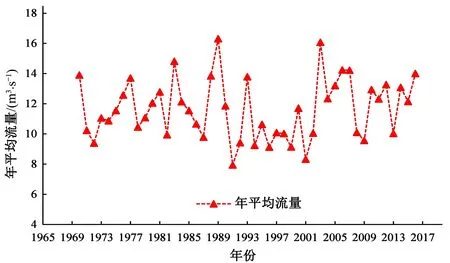
图2 西营水库1970-2016年径流变化过程Fig.2 Process of runoff change in Xiying Reservoir from 1970 to 2016

2.3 实例应用

选择西营水库1970-2016年实测径流资料以及中国气象局国家气候中心气候监测室 http:∥cmdp.ncccma.net/Monitoring/cn_index_130.php提供的130项气候系统指数(即88项大气环流指数、26项海温指数和16项其他指数)作为待选因子。

首先，采用互信息(MI)方法计算各待选因子与年平均径流序列的互信息量大小，因子初步优选结果如表1所示。

其次，在初步选定因子的基础上，根据主成分分析(PCA)原则进行预报因子组合取满足85%贡献率，得主成分得分系数矩阵如表2所示。将得分系数代入式(4)产生新的预测因子z1,z2,…,z5作为预报因子。

表1 西营水库预报因子初步优选结果Tab.1 Preliminary optimization results of forecast factors of Xiying Reservoir

表2 主成分得分系数矩阵Tab.2 Principal component score coefficient matrix

最后，利用MI-PCA方法筛选的预测因子作为模型的输入因子，对西营水库进行年平均入库径流预测。模型率定期和检验期设置如下：1920-2004年为率定期，2005-2016年为检验期。

为了验证基于MI-PCA的BP神经网络模型的预测效果，将预测结果与基于MI和PCA的BP神经网络模型进行对比。并考虑采用《水文情报预报规范》的相关方法对预报精度进行评价。评价指标具体如下：

(5)

式中：QR为预报合格率；M为预测值合格的次数(预测值和实测值之间的相对误差在±20%之间预测结果视为合格)；N为预报总次数。

只有当合格率达到80%以上的预报模型，才能用于作业预报。

3 结果与分析

MI、PCA、MI-PCA的模型参数结构和预报效果如表3、表4所示。

表3 MI、PCA、MI-PCA模型参数结构Tab.3 Parameter structure of MI, PCA, MI-PCA model

表4 MI、PCA、MI-PCA年径流预报精度评价结果Tab.4 Results of the accuracy evaluation of annual runoff forecast for MI, PCA and MI-PCA

3种不同预报因子筛选方法(MI、PCA、MI-PCA)的年径流预报效果图如图3所示。

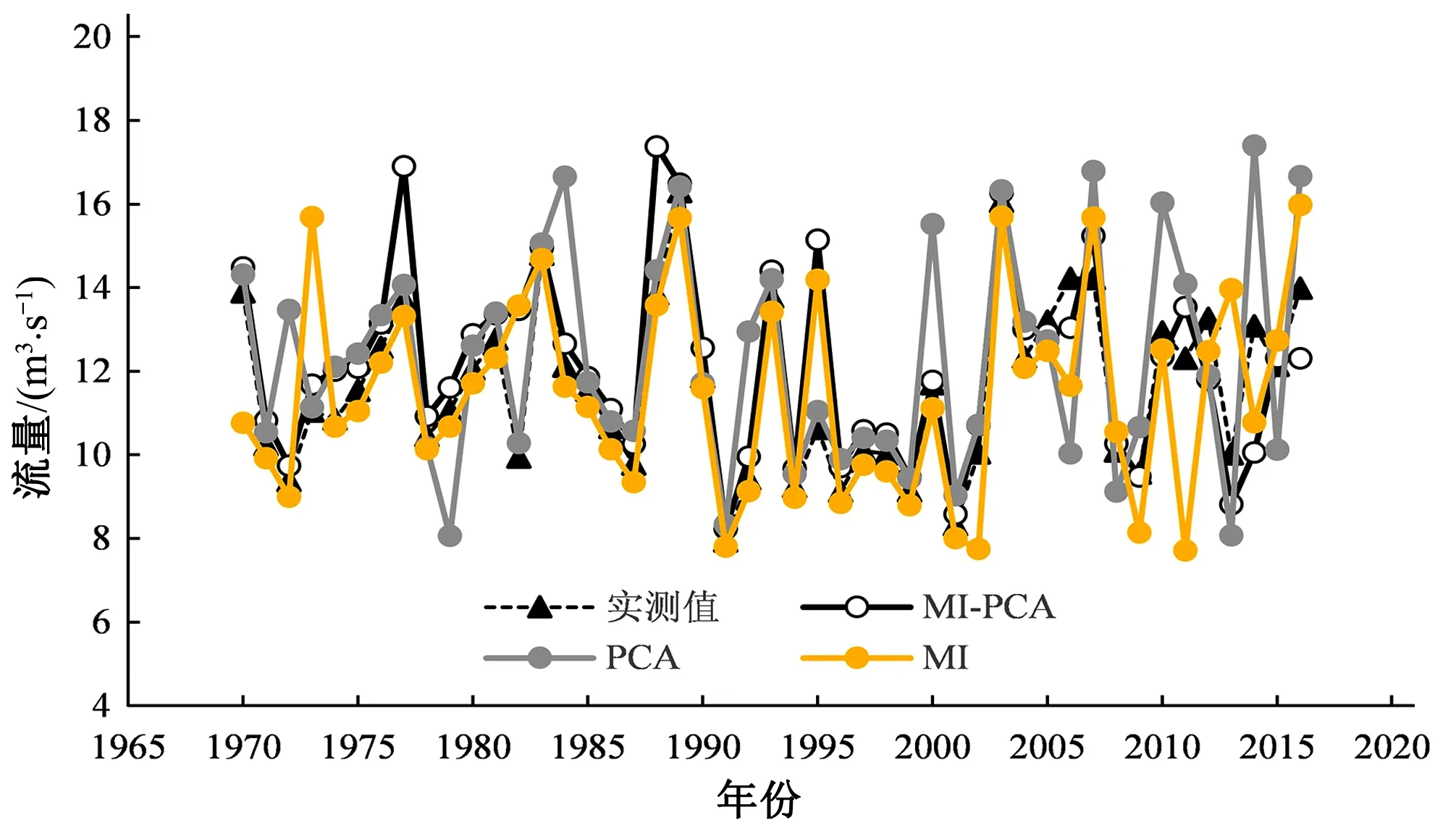
图3 西营水库3种不同预报因子筛选方法(MI、PCA、MI-PCA)的年径流预报效果Fig.3 Annual runoff prediction effect of three different forecasting factors screening methods (MI, PCA, MI-PCA) in Xiying Reservoir

由表4和图3可知，率定期MI、PCA和MI-PCA的合格率均大于80%；而在检验期基于PCA的BP预报模型合格率仅为75%，说明基于PCA优选预报因子构建的BP神经网络模型存在过拟合现象，模型可靠性较低；而MI、MI-PCA模型在检验期的预报合格率分别为83.33%和91.67%，预报效果较好。

4 结 语

在石羊河流域的中长期径流预报中，基于MI和MI-PCA的BP神经网络2个模型的预报精度都满足《水文情报预报规范》对于预报精度的要求，它可为石羊河流域中长期径流预测提供技术支持。整体而言，MI-PCA模型预报效果最佳，表明在互信息的基础上计算主成分，既充分考虑到了2个变量之间线性和非线性的关系，又可以舍去重叠部分的信息，减少原来变量的个数，能够更准确地描述预报因子与预报径流间复杂的非线性特征，是一种有效的中长期预报方法。

□