炭黑填充橡胶Mullins 效应研究

2019-11-13黄丽红

安徽化工 2019年5期

黄丽红

（福州大学至诚学院，福建福州350002）

炭黑颗粒增强的橡胶在单轴拉伸、压缩或剪切加载后，在卸载过程中表现出明显的滞回性效应，即卸载的应力明显小于相同载荷下的加载应力。对于没有变形历史的炭黑填充橡胶，伸长比逐渐增大的加载卸载循环应力应变曲线中，卸载曲线明显比加载曲线低很多，而重加载时，又稍高于卸载线。这种现象命名为Mullins效应[1]。

对于Mullins 效应，很多学者给出了本构关系[2-4]，其中Ogden-Roxburgh（1999）[5]提出的基于伪弹性理论（Pseudo-elastic model）的唯像模型，在加载卸载过程，利用该模型来计算能量耗散情况，不仅能用于单轴拉伸情况，也适用于双轴和多轴拉伸的情况。

本文将对不同炭黑填充含量的天然与丁苯共混橡胶进行不同伸长比的单轴拉伸实验，并使用Ogden 伪弹性模型，利用ABAQUS 软件对其单向拉伸加载和卸载循环进行仿真，并预测不同伸长比的拉伸循环。

1 本构模型

单轴拉伸情况下，对于炭黑填充橡胶这种不可压缩材料，Ogden 本构模型的应变能函数[6]如式（1）：

材料在加载-卸载-重加载-卸载的Mullins 循环中，发生了连续损伤，能量函数用来描述，加载与卸载的关系如式（2），为连续损伤变量，式（3）为Ogden-Roxburgh 损伤函数[5]，的表达式如（4）所示：

2 实验与仿真结果分析

本文中所得实验数据为在室温条件下进行的准静态单轴拉伸实验数据，试样为哑铃型，配方及炭黑填充体积比如表1 所示，表中各成分均以质量份表示。

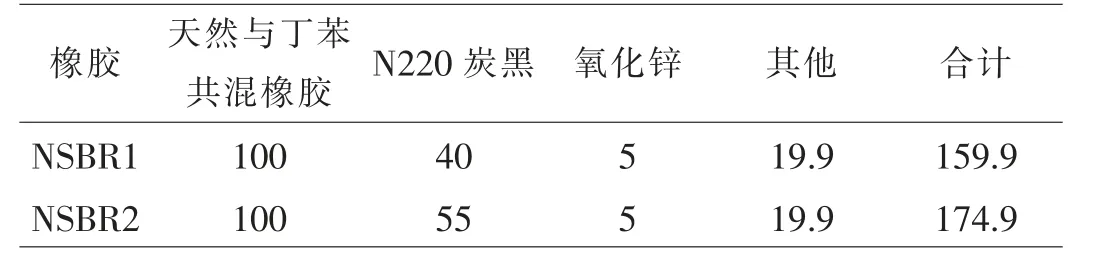
表1 橡胶配方表（质量份）

2.1 Mullins 效应仿真与实验

利用实验数据拟合Ogden 本构参数与伪弹性参数，见表2，运用ABAQUS 对两种橡胶进行不同伸长比的加载卸载仿真。图1 和图2 给出两种橡胶不同伸长比的实验数据与仿真曲线对比。

利用最大伸长比的卸载实验数据与加载实验数据拟合得到r 与m。观察图1 和图2 的曲线可以发现，仿真效果能够很好地吻合实验曲线，尤其对于加载曲线和最大卸载曲线。但是随着循环伸长比的减小曲线精度降低。因此，只是利用一个循环的数据拟合的伪弹性参数难以准确地描述不同伸长比循环的卸载情况。要提高精度，对于每个循环的伪弹性参数需要分别进行计算和仿真。本文将寻找不同循环之间伪弹性参数的变化规律。

2.2 不同伸长比加载卸载循环伪弹性参数的变化规律

本文使用NSBR2 橡胶进行了6 个加载卸载循环实验，循环伸长比为λ=1.3，1.6，1.9，2.1，2.3。采用Ogden 本构关系对主加载实验数据进行拟合，分别利用各个循环的卸载实验数据计算出λ=1.3，1.6，2.1，2.3 循环的伪弹性参数，找出规律，预测λ=1.9 的卸载曲线。计算伪弹性参数，可以发现，m/r 或m*r 都与伸长比之间存在明显的多项式变化规律，拟合出多项式见式（5），规律如图3所示。

表2 Ogden 本构与伪弹性参数拟合结果

图1 NSBR1 实验与仿真曲线对比图

图2 NSBR2 实验与仿真曲线对比图

图3 伪弹性参数变化规律

将λ=1.9 的循环，带入多项式（5）计算可得：r=1.318，m=0.387 3 MPa。如用该循环的卸载和主加载曲线拟合的数据为：r=1.352，m=0.389 2 MPa。将预测所得参数带入ABAQUS 中仿真得到主加载和不同伸长比的卸载曲线如图4 所示。

从仿真结果可以看出，对伸长比λ=1.9 的循环，用多项式计算所得参数仿真的曲线，与利用最大卸载循环拟合所得参数仿真的曲线，在卸载初始，与实验数据稍有偏差，但是在小变形时，该循环用多项式计算参数仿真的曲线比利用最大循环拟合参数仿真的曲线来得精确，因此，利用多项式找出伪弹性参数的规律，可以准确描述炭黑填充橡胶不同拉伸比的Mullins 循环。