长江经济带工业碳排放收敛及其驱动因素分析

胡 宇

一、绪 论

现阶段，经济发展是国家和地区最为重视和长期追求的目标，也是改善国家和地区环境，提高社会福利待遇，实现社会长治久安的前提条件（程秀花等，2017）[1]。我国已明确规定在2020年到来之前，工业碳排放强度要较2005年降低40—45个百分点。从“十二五”规划以来，我国一直强调加强管控能源消费总量，针对长江经济带地区制定了应达到的碳强度数值等相关标准。然而，无论是碳总量管控数值，还是强度数值，都未能彻底解决制约长江经济带各地区经济发展的因素，这样就可能给地方政府减排工作带来诸多困难，政策的可行性和有效性将会大打折扣（王少剑等，2017）[2]。因此，要想实现碳减排指标的同时又能推动区域经济的发展，各级政府必须对碳排放的分布、发展趋势及其影响因素展开更深入地研究，找到问题的根源，解决问题的主要矛盾，制定实际可行的政策措施，让减排工作能够得到较好的处理。

二、数据来源、数据处理及模型方法

（一）长江经济带碳排放驱动因素的数据来源与数据处理

1.数据来源

文章中的数据主要来源于国家统计部门数据库、国家环境保护数据库、国家能源统计部门数据库，同时也参考了长江经济带各省市相关统计数据库，年份主要集中在2000—2018年。

2.指标权重的选取与确定

指标选取的正确性和合理性是系统分析与评价的基础，本文涉及城市化和环境两个系统，在遵循综合性、客观性、可比性等原则上，建立以下指标体系，见表1。

表1 指标详情

文中统计核算碳排放量的原始数据主要取自于长江经济带2000—2018年每年原煤、焦炭、原油、燃料油、汽油、煤油、柴油和天然气等8种能源消费的具体数据。另外，文章关于城市化进程中影响碳排放因素相关数据则取自各省市地区统计年鉴，并通过统计核算软件进行数据整理汇总减少误差。

（二）长江经济带碳排放收敛模型

1.α收敛

α收敛是生态环境经济学中影响生态环境指标的离散程度减小的状态。它可以表现出个别地区与全国整体水平的偏离程度。文中分别通过极差、标准差和α系数考核α收敛，当以上三个指标随着时间的增加而减少时就会出现α收敛。

（1）标准差指的是离散程度，即相对于全国平均水平各地碳强度的离散程度，表达式为：

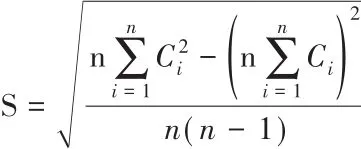
式中省区数用n表示，第i个地区的碳排放强度用Ci表示。

（2）极差指的是衡量两个最值（最大值与最小值）两者的差额程度的参量，可以表示为R=Cmax-Cmin，其中，Cmax为碳强度的最大值，Cmin为碳强度的最小值。

（3）α系数大多数情况下可以当作估测各地碳强度偏离均值的水平，表达式为：

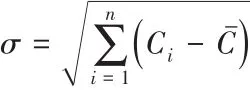
式中省区数用n表示，第i个地区的碳排放强度用Ci表示，Cˉ是全国碳强度的平均水平。

2.β的绝对收敛

在其他条件确定的前提下（产业构成、能源利用和收入），β的绝对收敛情况就是各地区的碳排放的强度最后可以同时收敛于相同的稳态水平。表达式如下：

式中不同年份用t表示，第i个地区的t年份的碳强度用Cit表示，残差项用μit表示。当β小于0时，就出现绝对收敛。

3.β的条件收敛

β条件收敛就是在一些经济条件不同的情况下，比如产业、能源消费结构等，各省市区的碳排放强度最终会收敛于不一样的稳态水平。表达式如下：

式中不同年份用t代替，不同区域用i代替，第i个区域的t年份的碳强度用Cit代替，第二产业产值、第三产业产值、城市人口占比、城镇建成区面积和人均 GDP 分别用 T、S、R、F、E 表示，残差项用μit代替。在β小于0的时候，属于条件收敛。

（三）其他模型与方法

1.STIRPAT模型

美国生态学家在上世纪七十年代针对经济发展与生态环境的联系提出了IPAT模型，即I=IPAT。Rose在IPAT之后又通过对居民的富裕程度、科学技术的回归采取生态压力的随机测算结果得出生态压力随机模型，也即STIRPAT模型（宋晓晖等，2018）[3]。

根据长江经济带的总体经济发展态势，从中选取作为影响城市化过程CO2排放量的指标，即第二产业产值、第三产业产值、城镇人口占比、城镇建成区面积、城镇居民人均 GDP、能源的强度。通过STIRPAT，得出这些参数与碳排放量内部联系的有关模型。通过回归分析确定模型系数，得到如下公式：

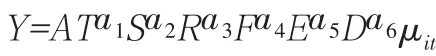
对表达式取对数：

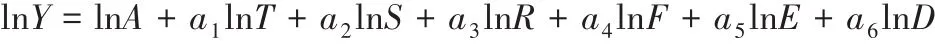
式中碳排放总量用Y表示，常数用A表示，第二产业产值、第三产业产值T、S，城镇人口占比、城镇建成区面积分别为R、F，人均可支配收入为E，能源强度用D表示，随机模型项用μit表示，模型弹性系数用ai表示，即带来Y的ai%变化是由于T、S、R、F、E和D每发生1%的变化时引起的。

2.偏相关关系探讨

本文运用SPSS19.0中影响城市化进程及碳排放相关的指标与碳排放量之间的时间序列的数据所运行的偏相关分析，可得到各参数与碳排放量的偏相关系数，经过显著性检验来辨清是否能作为碳排放量的影响驱动因素。

3.主成分分析

主成分分析是指把之前的多个变量简化为更少的几个综合指标的一种计量分析法，是一种降维分析的方法。首先，通过SPSS19.0中的主要成分辨析法对最初的自变量进行研究和辨析，找出解释力很高的整体参数。接着，运行普通最小二乘回归，得到因变量与整体之间的线性表达式。最后将综合变量与自变量之间存在的线性关系式代入因变量与整体之间的线性表达式中，就能得到因变量与自变量间的表达式，在STIRPAT模型中得出最初变量的驱动因子弹性系数和贡献率。

三、长江经济带碳排放指标核算与实证分析

（一）长江经济带碳排放指标核算

碳排放的产生主要是由于化石能源消费引起的。能源消费引起的缘由有很多，这些影响因素之间的关系同样很复杂，如果采用较多的驱动因素，自然会造成数据的繁琐化。一次能源消费总量参数折算为标准煤参考系数就可看作是碳排放值（CE），计算累计的碳排放量，主要包括煤炭、石油、天然气三大能源，其表达式是：

表达式中，i=l，2，3，分别代表：煤炭、石油、天然气，E为能源消费的总量（单位：万吨），第i种一次能源消费所占的比例用Wi表示，第i种一次能源的消费量用Ei表示，第i类一次能源的碳排放系数δi表示，其中，煤炭δi=0.7229，石油δi=0.5573，天然气δi=0.4225。

结合2000—2018每年能源消费所占比率和能源消耗量E，得到碳排放量如表2所示。

为更加形象地了解2000—2018年长江经济带碳排放情况，根据表2中碳排放统计核算可以绘出碳排放量的变化折线图，如图1。

根据表2和图1发现，2000—2004年碳排放量相对而言较稳定，2004年后碳排放量一直处于上升趋势，尤其是2007—2012年，碳排放量上升很快，随后上升的速度逐渐放缓，到2014年，又开始加速增长，再到2016年增长速度又出现放缓，并逐步趋于稳定状态。

（二）长江经济带碳排放收敛分析

根据公式（1）（2）进行计算整理，可得到表 3数据。

由表3可知，2000—2018年期间，长江经济带各地单位GDP的CO2排放量伴随时间增加逐步减少，碳强度在2007—2012年期间是不稳定的，但从整体角度来观察是下降趋势。从整体角度来看碳强度平均减少了0.4514t/万元，年度均减少2.191%。其中，贵州、云南两省碳强度最高，然而从整体来看碳排放水平仍有较大程度的减少；上海、江苏、浙江等煤炭资源缺乏的省市区碳强度最小。在样本期间内，单位GDP的CO2排放量稍低省份的碳强度的下降速度要明显慢于单位GDP的CO2排放量稍高省份，另从表4中的极差、标准差、σ系数等统计结果也表明，长江经济带各地碳强度收敛。

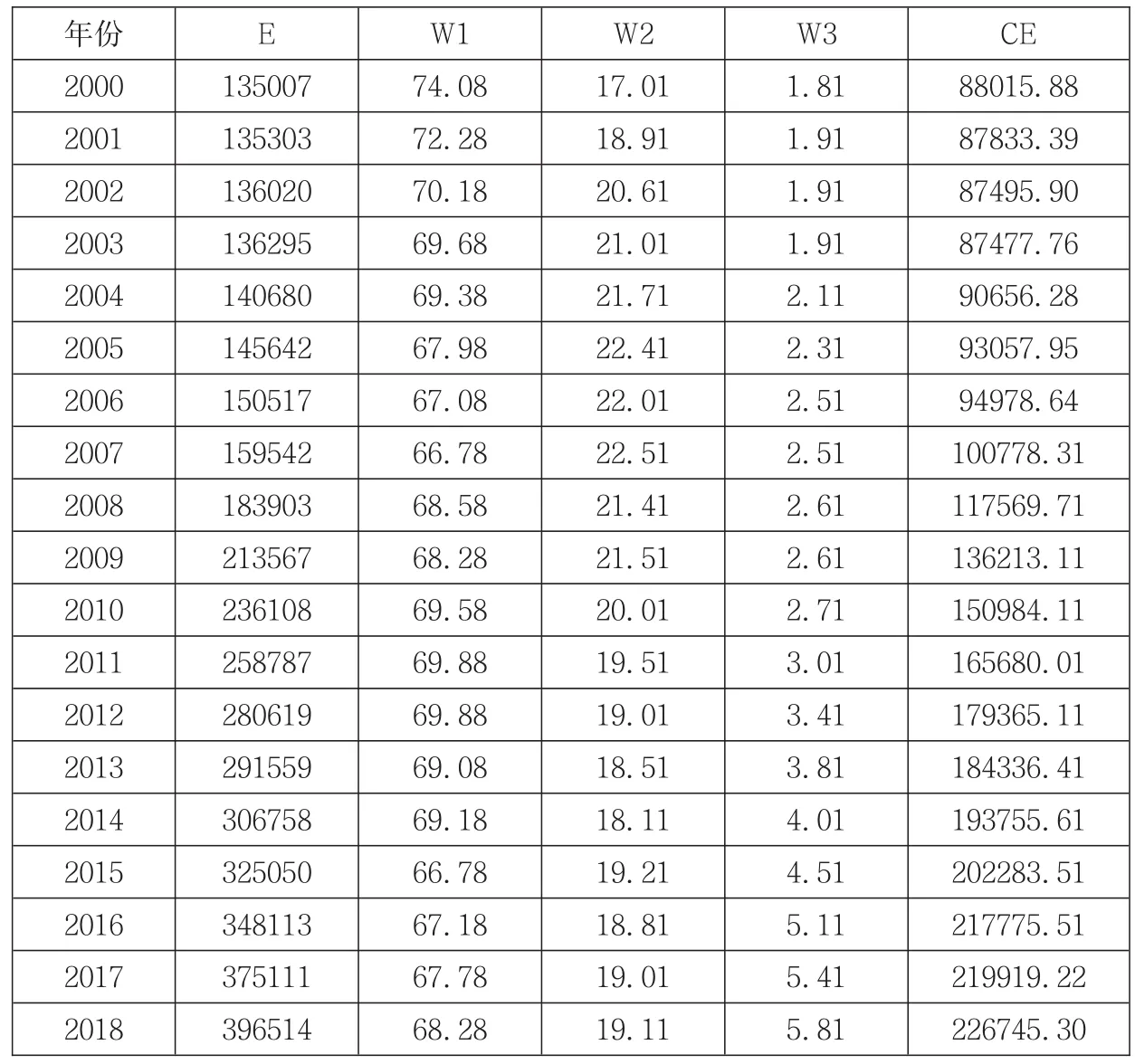
表2 2000—2018年碳排放量核算表

图1 2000—2018年碳排放量的增长折线图 （单位：万吨）

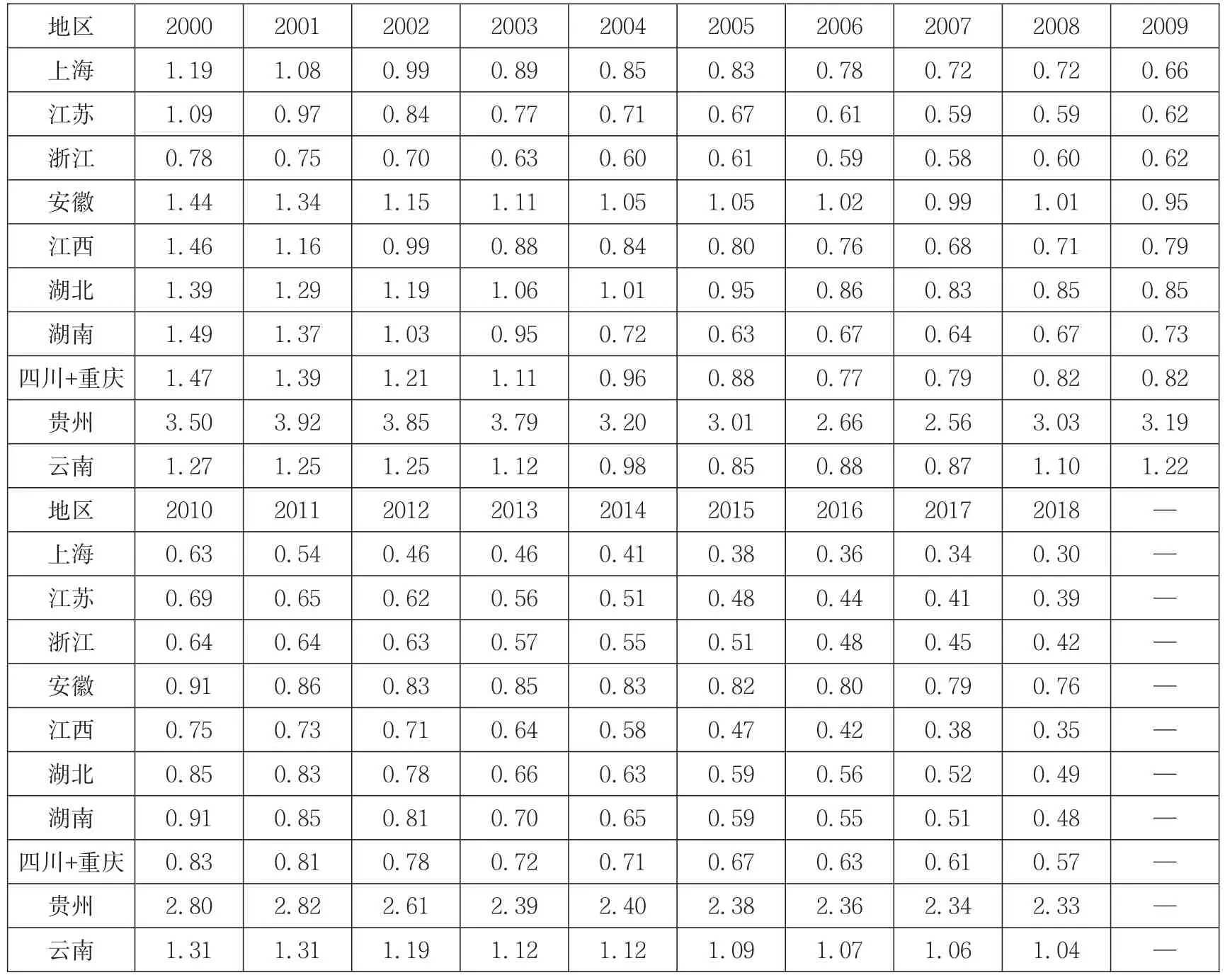
表3 2000—2018年长江经济带各地碳强度变化情况 （单位：t/万元）

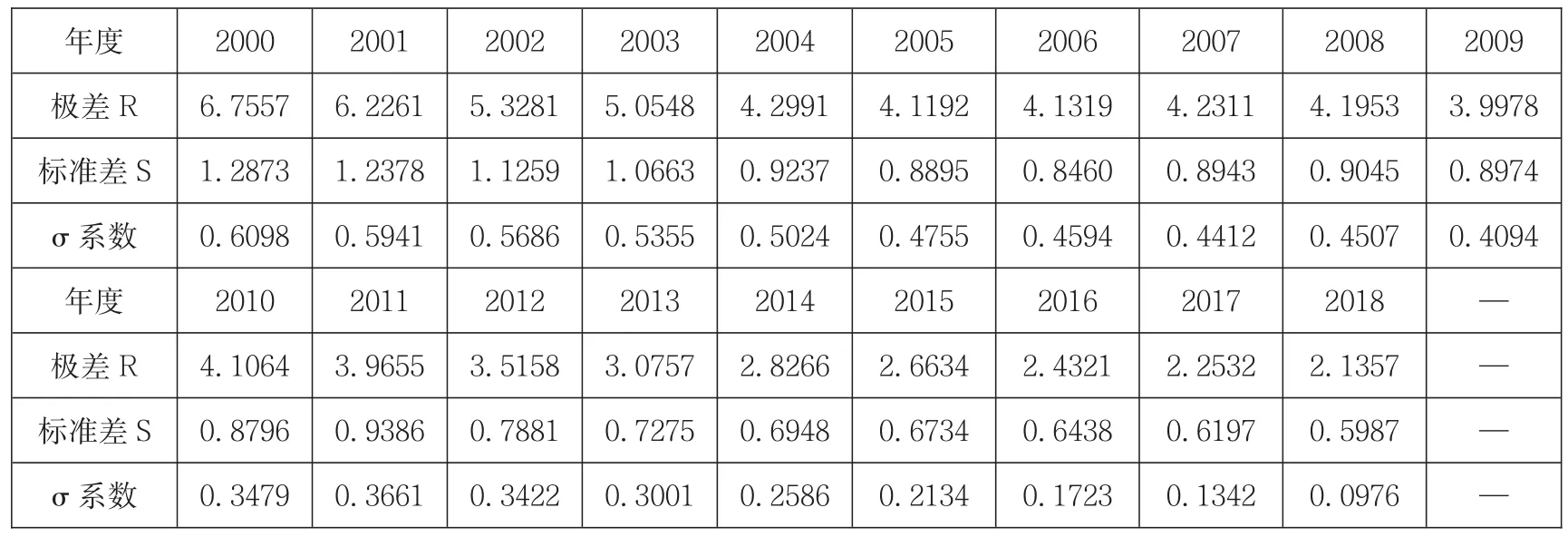
表4 2000—2018年长江经济带地区间碳强度差异变化趋势

关于β绝对收敛的具体情况，表5中，利用2000—2018年长江经济带各地碳排放强度的样本数据和Eviews 6.0，检验单位GDP的CO2排放量是否绝对收敛。首先看F—统计量和Hausman检验，结果显示两者都拒绝原假设，表示模型存在个体固定效应，所以回归分析可以通过个体固定效应模型实现。

从表 5得知，LOG（C）的系数为负，且在0.010%的基础上显著不是0，说明回归方程结果很好。可以推断2000—2018年间，长江经济带内各地单位GDP的CO2排放虽然不一致，然而β绝对收敛是显著的，所以长江经济带各地碳强度差异有降低的态势。

β条件收敛，根据公式（2），采用2000—2018年长江经济带各地第二产业产值、第三产业产值、城市人口占比、城镇建成区面积和人均GDP等数据，最初借助F—统计量和Hausman检验，若结果均拒绝原假设，表示模型存在单个固定效应，则我们可以根据单个固定效应模型进行回归分析。这里正好符合，表6即为β条件收敛检验结果。

表6中，LOG（C）的系数为负，且在0.01%基础上显著不是0，人均GDP、产业结构、能源结构、出口占GDP之比分别在0.50%、2%、60%、15%的水平上显著不是0，由此可以看出，由于各省区经济发展水平、产业、能源结构等各种经济条件的不同，长江经济带各地间碳强度在2000—2018年存在β条件收敛。

表7中，对碳强度的影响驱动因素进行了更进一步研究，可假设方程：

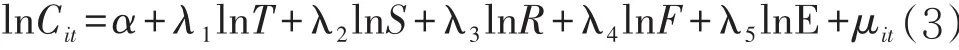
式中，各个年份用t表示，第i个地区t年份的碳强度用Cit表示，第二产业产值、第三产业产值、城市人口占比、城镇建成区面积和人均GDP分别用T、S、R、F、E 表示，残差项用μit表示。借助 F—统计量和Hausman检验，结果均拒绝原假设，表示模型存在单个固定效应，可根据单个固定效应模型进行回归分析。如表7，模型1、2、3中，针对碳强度的影响明显的有 LN（T）、S、R 和 F。其中，产生正向影响的第二产业产值、第三产业产值是建立在0.01%的显著性水平上，两者的变化是同方向的；城市人口占比与城镇建成区面积在1%的显著性水平上也是正向影响，城市人口占比与碳强度排放量同方向变化；在0.01%的显著性水平上，人均GDP同样也是正向影响，即随着人们生活水平的不断提高，碳强度也在不断增加（黄立洪等，2016）[4]。

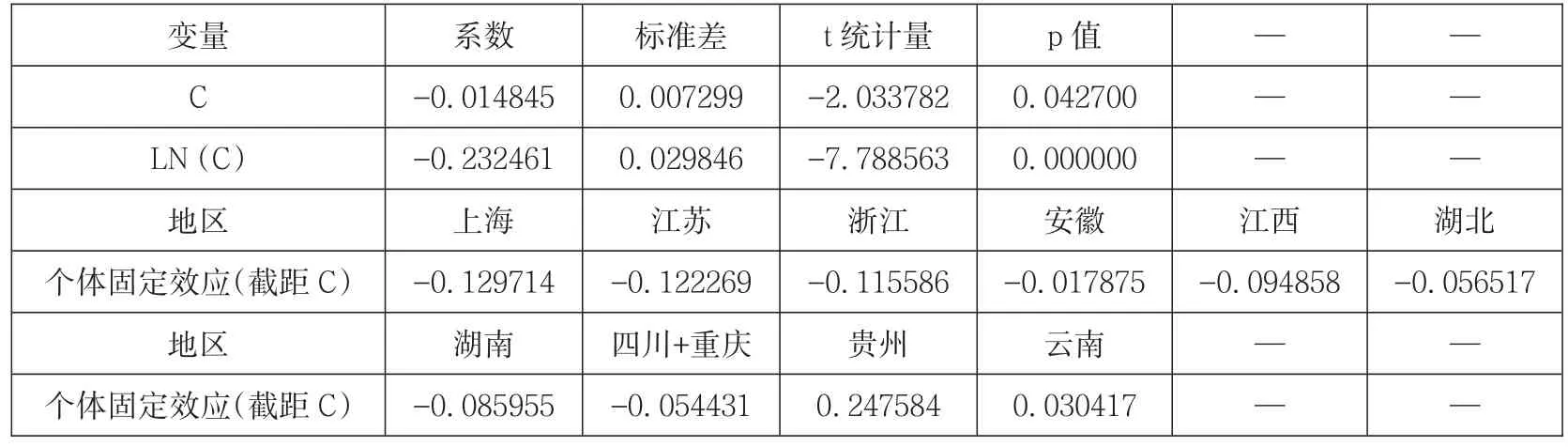
表5 长江经济带地区间碳强度的β绝对收敛检验结果

表6 长江经济带地区间碳强度的β条件收敛检验结果

表7 长江经济带地区间碳强度影响因素分析结果

从表8可知，2000—2018年长江经济带每年的平均能源消耗总量、碳排放量以及人均碳排放量均呈现逐年递增状态。从2000年到2018年这十几年中长江经济带各地区能源强度和碳排放强度显示出了明显的下降趋势。其中不难发现能源消耗增大和环境承载力下降造成的碳排放上升的趋势，大部分原因可以认为是由于社会经济发展需要带来的城市化进程的加快，同时也可以看到2008年以来，整个长江经济带经济发展的核心产业是第二产业，主要包括工业区建设、房产开发、旧城新建等，还包括以电力、冶金、水泥加工等6大重化工业发展而迅速带动了长江经济带整个区域的能源消费持续上升，结果使得能源消耗和碳排放量不断增加。但是，最近几年来，因为各省市积极响应国家政策，加强生态环境保护，对高耗能、重污染的企业进行整治并提高了相关标准，通过鼓励提高科学技术水平使得循环经济和低碳经济得到很好地实施，逐步提高了能源利用率，使得长江经济带碳排放强度和能源强度出现了持续下降的态势，碳排放强度呈减少态势。

表8 长江经济带2000—2018年平均能源消费和碳排放时间序列

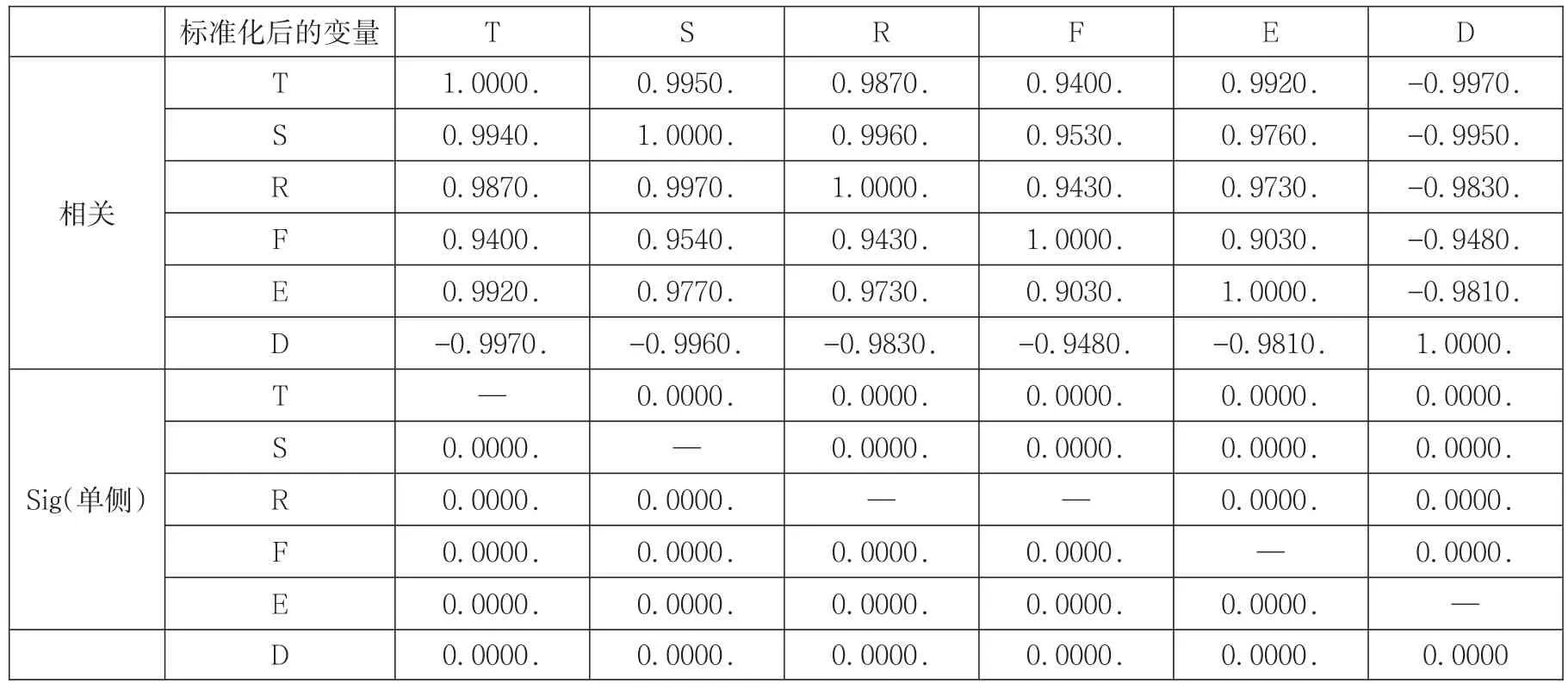
表9 主成分分析相关系数矩阵

（三）稳健性检验——长江经济带驱动因素的主成分分析

为保证研究的结论更加客观、科学，需对上述结果进行稳健性检验，使评价结果更有说服力，同时也使得整个分析更具逻辑性。

偏相关讨论。第二产业产值、第三产业产值、城区人口占比、城镇面积、能源的强度分别用T、S、R、F、E、D作为参数表示，因变量用Y表示，偏相关讨论可以通过SPSS19.0实现。分析结果显示，这些指标和相关参数显然大于0.9，在0.01水平（双侧）上显著相关，符合显著性检验，则可认为这六个影响城市化发展的因素都是碳排放总量的驱动因素。

因子主成分分析讨论。利用上述的六个指标和碳排放量最初时间序列数据进行对数变换，为降低各变量间的量纲和数量级差异，让数据更具可比性，将数对变换后的数据进行标准化处理，将标准化后的数据输入SPSS19.0运用主成分分析处理。结果如表9所示。

从表 10 得知，标准化后的自变量 T、S、R、F、E、D被进行分析与筛选后，可以采取2个主成分，即综合变量用Z1、Z2显示，解释因变量的 97.582%和99.379%能够通过Z1、Z2实现，而且t检验的Sig值小于0.01（见表8），拟合程度较好。由表11显示得分（贡献率）矩阵，显示综合变量Z1、Z2与因变量的联系，表达式可为：

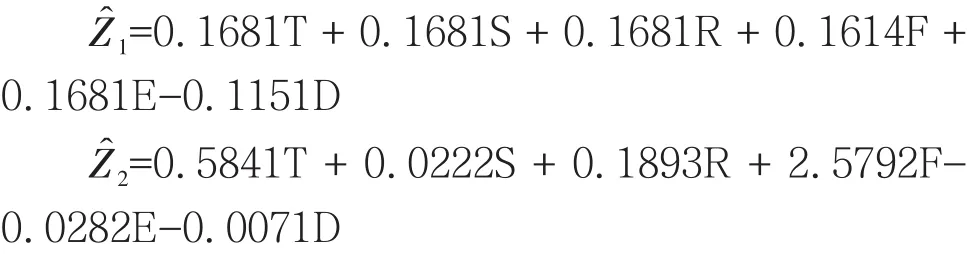
考核拟合优度的统计量可以利用比较判定系数R2，R2越大就说明拟合度越高，通过以上两式，被解释变量、解释变量与工具变量分别用 Yˆ、Zˆ1、Zˆ2表示。随后回归拟合，得到模型的比较判定系数R2、F值、标准误差、t检验的 Sig值，分别对应为 0.842、49.38、0.098、0，显然 Sig 值等于 0.0000，而小于0.01，模型拟合较好。

根据表 12 可得到综合变量Zˆ1、Zˆ2与 Yˆ的关系式为：

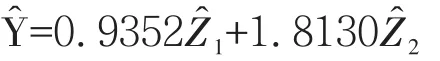
根据主成分因子载荷量构成一个综合评价函数，将 Z1、Z2代入即可得到：

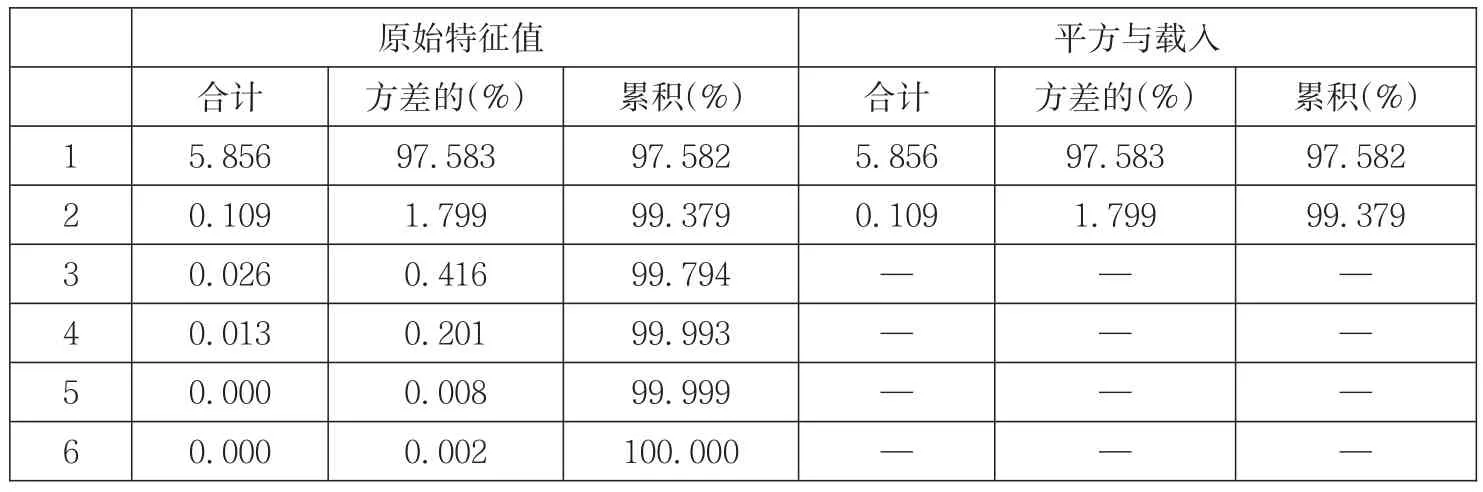
表10 主成分分析解释总方差

表11 主要构成得分系数（贡献率）分布图

表12 模型变量系数（载荷）

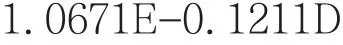
由上式可得出长江经济带2000—2018年城市化进程中，碳排放量逐年增长的驱动因子模型：

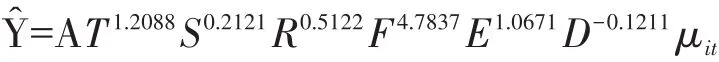
通过公式可知，城市化过程中，影响长江经济带2000—2018年碳排放量的第二产业产值、第三产业产值、城市人口占比、城市建成区面积、居民人均GDP、能源强度等驱动因子的弹性系数分别是1.2088、0.2020、0.5023、4.7938、1.0660、-0.1202，其中1.2088表示当第二产业产值上升1%时，碳排放量将随之增加1.2088%，其他弹性系数与之类似。

本文借助主成分分析法和SPSS19.0等软件，对长江经济带2000—2018年碳排放相关数据进行处理和分析，初步讨论了长江经济带碳排放驱动因素的作用及其相关关系。

1.第二产业产值、第三产业产值、人口占比、城市建成区面积、居民人均GDP五个影响因素与碳排放量增长表现出正向关系。按影响重要性排序应是：建成区面积、第二产业产值、居民人均GDP、城市人口占比和第三产业产值。产生这种现象的原因可能是近年来长江经济带正进行着新型城镇化建设，同时伴随着国家经济结构的调整和重点产业布局的优化，整个长江经济带的城镇建成区面积在逐步扩大。除此之外，长江经济带工业发展速度明显加快，使得整个区域的工业化水平得到了很大提高，从而引起能源消耗量增加，最终导致碳排放量随之逐年增加。

2.在2000—2018年期间，长江经济带的碳强度与碳排放量增长存在着负相关关系。其原因可能是整个区域在城镇化发展过程中，通过鼓励技术创新，强调绿色环保意识，使得能源利用率得到了有效提高，最后碳排放量增加带来了碳强度的减少（肖英等，2018）[5]。

四、实证结论与建议

文章基于2000—2018年长江经济带九省二市相关统计资料，在碳排放研究中加入收敛等相关理论，较为系统地研究了长江经济带各省市之间单位GDP的CO2排放量是否存在收敛性以及存在的影响驱动因素，得出两点结论：首先，长江经济带各省市之间碳强度有σ收敛、β绝对收敛和β条件收敛，表明可能降低单位GDP的CO2排放量的区别；其次，影响长江经济带碳排放的原因分别是产生负向、正向、正向和正向的影响的经济发展水平、人口数量、产业结构情况和城市化水平等因素，在其他条件不变的前提下，能够降低我国长江经济带碳排放强度的主要措施是提升经济发展水平、减少第二产业产值占GDP的比重，以及控制城市人口规模。

为保证研究结论更加客观、科学，进行了稳健性检验，且最终通过了稳健性检验。通过计算出城市化进程中影响碳排放的驱动因子弹性系数，得出以下两点结论：首先，对于城镇化进程中的长江经济带，主要是由于第二产业产值、第三产业产值、城市人口占比、建成区面积、居民人均GDP的增加带来碳排放量的增加（程秀花等，2018）[8]。其次，长江经济带在城市化进程中碳排放量表现出逐年上升趋势。

党的十八大以来，我国政府把生态文明建设和生态环境保护摆在重要的战略地位。继2016年7月1日全面推行资源税改革后，11月国务院通过了《“十三五”生态环境保护规划》，随后又颁布了《环境保护税法》（薛小青，2018）[6]。为实现长江经济带低碳经济和可持续发展目标，提出以下几点建议：

1.从城市发展和科学增长出发，应该严格执行国家新颁发的土地利用规划，树立科学发展观，科学推进城镇化进程，调整城镇空间布局，严格控制城镇用地规模。

2.加强产业结构调整，加速整个经济发展过程中能源利用结构的转型，大力发展绿色环保企业，因地制宜，同时不可忽视第三产业的发展。

3.在城市化进程中，要提高人口流动的方向性，加快产业结构调整，“绿色建筑”“生态住宅”等理念都值得提倡，低碳环保理念需得到具体落实。

4.在城市化进程中，不断强化节能环保意识，加强绿色消费理念的宣传力度，真正将口号、理念落实到实处。