基于改进DRLSE水平集模型的图像分割

魏晨晨，羿旭明

基于改进DRLSE水平集模型的图像分割

魏晨晨，羿旭明

(武汉大学数学与统计学院，湖北 武汉 430072)

针对DRLSE水平集模型对噪声敏感、依赖初始轮廓位置以及演化速度缓慢等不足，利用小波变换和小波阈值去噪的方法，构造对噪声不敏感的边缘信息刻画矩阵，定义基于图像信息的边缘停止函数和自适应权重系数，获得了改进的DRLSE水平集图像分割模型。利用有限差分法对模型求解，并采用Jaccard相似度作为评价模型的定量分析方法，数值结果显示改进的模型及算法对图像分割的有效性，克服了DRLSE水平集模型分割含噪图像以及定义初始轮廓位置的局限性，提高了DRLSE水平集模型的计算效率和图像分割精度。

图像分割；DRLSE水平集；边缘停止函数；自适应

近年来，由OSHER和SETHIAN[1]提出的水平集方法已经被广泛地应用于计算机视觉的图像分割领域[2-4]。水平集方法的基本思想是将轮廓曲线表示为在较高维度中定义的隐式函数的零水平集，并根据相应的偏微分方程演化水平集函数[5]。活动轮廓模型作为图像分割的重要工具之一，按照轮廓线表达形式的不同分为参数活动轮廓模型[6-7]和几何活动轮廓模型[5,8-10]。与参数活动轮廓模型相比，几何活动轮廓模型基于曲线演化理论和水平集方法，具有对初始轮廓不敏感、能够适应曲线拓扑结构变化以及可以得到稳定唯一的数值解等优点[8]。最早的几何活动轮廓模型是由文献[3]和文献[4]分别提出的测地线活动轮廓模型(geodesic active contour，GAC)，在图像梯度变化较大时该模型可以进行稳定的目标边界检测[9]。但是为了保证水平集稳定而有效地演化，需要在演化过程中重新初始化水平集函数。

为了避免重新初始化水平集函数带来的时间代价和数值偏差，LI等[5,10]提出了距离保持水平集演化模型(distance regularized level set evolution，DRLSE)。DRLSE模型无需进行水平集函数的重新初始化，并且在利用有限差分法数值求解时可以使用较大的时间步长，极大地提高了水平集演化速度。然而该模型存在以下不足：①边缘停止函数基于梯度信息，从而对噪声敏感，在分割含噪图像时，水平集容易陷入虚假边缘导致分割效果不理想[11]；②在图像的弱边界处，图像梯度小，使得边缘停止函数值较大，演化曲线容易越过目标边界；③能量泛函的权重系数是常数，不能根据图像信息自适应地调整符号和大小，水平集演化不具有自适应性。

针对DRLSE模型的不足，研究者提出了许多改进方法。HE等[12]利用Laplace算子在图像边界两侧符号相反的性质构造出使水平集演化方向具有自适应性的权重系数。但是，Laplace算子的计算基于二阶导数，使得模型对噪声敏感。LIU等[13]将归一化局部熵引入到边缘停止函数中以减弱模型对噪声的敏感性。但是，归一化局部熵存在的块效应影响了分割结果的精确性。小波变换具有多分辨分析的特性，在图像去噪[14]和边缘检测[15-16]等方面发挥着重要作用。本文基于阈值处理后的小波系数构造边缘信息刻画矩阵，通过定义新的边缘停止函数和自适应权重系数，提高了DRLSE模型的分割效率以及分割含噪图像的有效性。

1 DRLSE水平集模型

设为图像区域，()为定义在上的水平集函数。DRLSE模型的能量泛函[10]表示为

其中，第1项是惩罚项，用于保证水平集曲线在演化过程中的光滑性；第2项和第3项分别是长度项和面积项，其作用是引导水平集向目标边界演化。正常数，和常数为各能量项的权重系数；(·)为能量密度函数；∇为梯度算子；(⋅)和(⋅)分别为Dirac函数和Heaviside函数。边缘停止函数()定义为

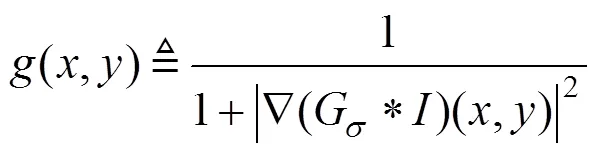
模型使用双势阱函数[10]作为能量密度函数

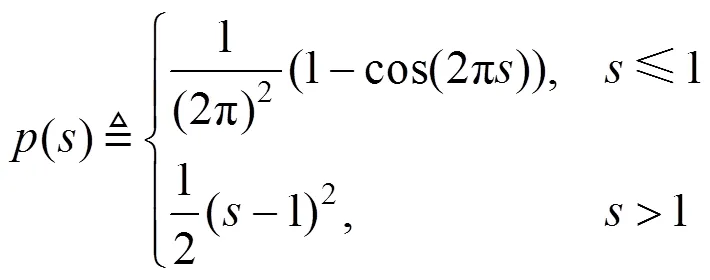
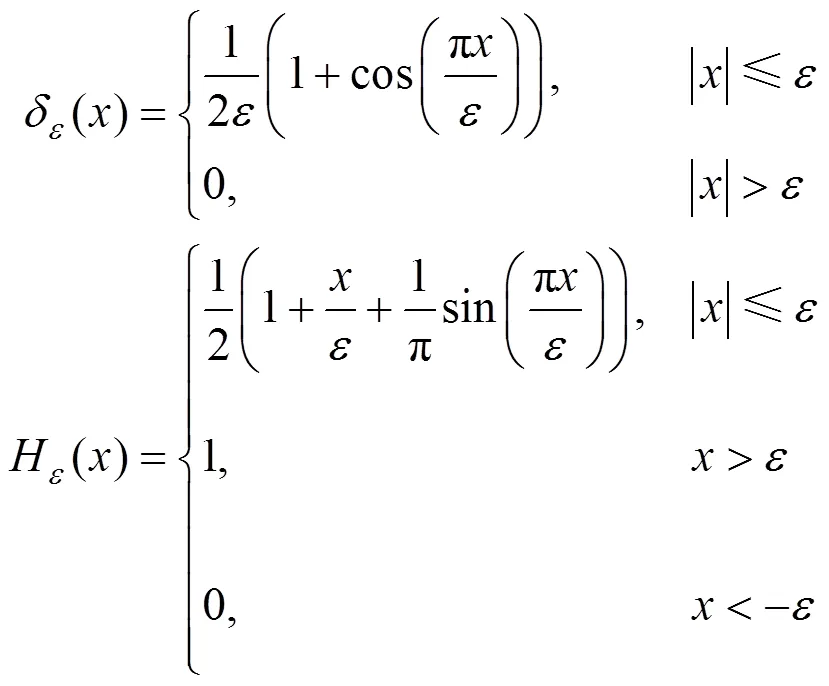
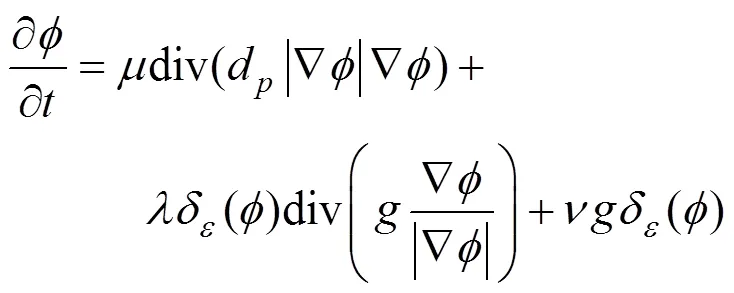
2 对DRLSE模型的分析

式(2)定义的边缘停止函数基于光滑图像的梯度，水平集在梯度信息的引导下演化。相比于传统的活动轮廓模型[6-7]，DRLSE模型能够准确而稳定地完成对目标物体的分割[10]。但是在分割含噪图像时，演化曲线受噪声干扰容易陷入虚假边缘。如 图1(b)所示，DRLSE模型可以有效分割出无噪声图像中的目标物体；图1(c)~(d)是向原图添加方差()分别为0.01和0.10高斯噪声后的分割结果，可以看出，随着噪声的出现和增强，演化曲线受到的干扰程度变大，目标物体得不到有效分割。

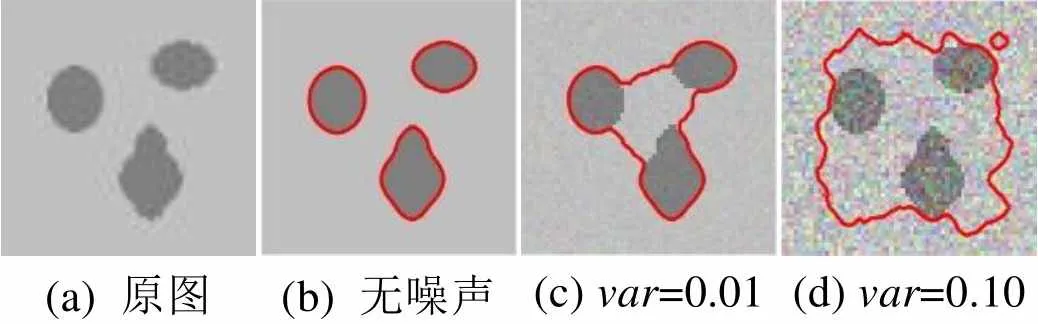
(a) 原图(b) 无噪声(c) var=0.01(d) var=0.10

权重系数是预先设定的常数。一方面，水平集根据的符号进行收缩演化(>0)或扩张演化 (<0)，初始轮廓必须设置为包围目标或在目标内部(或外部)。一旦初始轮廓与目标区域相交如图2(a)，模型在>0 (图2(b))和<0 (图2(c))的情形下均不能有效地进行图像分割。另一方面，当||过小时，水平集演化缓慢容易陷入局部极小值(图2(d))；而当||过大时，容易出现边界泄漏(图2(f))。

(a) 初始轮廓(b) v>0(c) v<0 (d) v=0.5(e) v=1.5(f) v=2.5

3 本文模型

3.1 边缘信息刻画矩阵

文献[16]提出的基于小波系数的边缘信息刻画函数，使得水平集在演化过程中能够迅速捕捉到图像的边缘，从而更加准确和高效地分割图像。但是对于含噪图像，图像的细节和噪声经小波分解后均体现在细节系数部分。因此，以上边缘信息刻画函数对噪声敏感。

本文首先对图像(,)进行层小波分解，得到近似系数A以及水平、垂直和对角方向的细节系数1,···,H,1,···,V,···,1,···,D在构造边缘信息刻画矩阵前，小波分解系数按以下方式进行处理：

(1) 使用如下函数对各尺度细节系数进行阈值处理

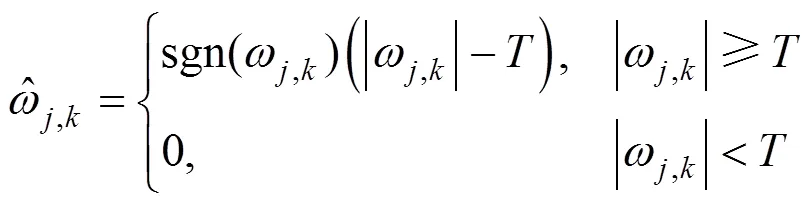
再对矩阵进行归一化处理，得到边缘信息刻画矩阵norm。

在图像光滑区域，小波系数梯度幅值小，矩阵元素norm(,)较小；在目标边界处，小波系数梯度幅值大，矩阵元素norm(,)较大。图3(a)是边缘深度凹陷图像，其边缘信息刻画矩阵的图像表示如图3(b)所示，可以看出矩阵norm有效地刻画出图像边缘。向原图添加方差分别为0.01和0.10高斯噪声后，对应的边缘信息刻画矩阵的图像表示如图3(c)~(d)所示。可以看出，随着噪声的增强，矩阵norm表现出对噪声的鲁棒性。

(a) 原图(b) 无噪声(c) var=0.01(d) var=0.10

3.2 新的边缘停止函数

为了提高DRLSE模型分割含噪图像的有效性，本文将边缘信息刻画矩阵norm引入到式(2)中，定义新的边缘停止函数new(,)为

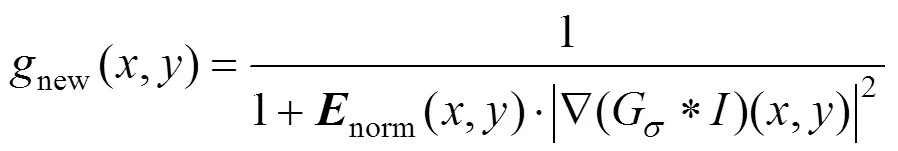
由式(18)可知，new(,)与图像梯度和小波系数梯度幅值成近似反比关系，并且具有在图像光滑区域接近1和在目标边界接近0的性质。而在含有噪声的图像区域，矩阵元素norm(,)较小，new(,)具有较大的值，避免了演化曲线陷入虚假边缘。此外，矩阵norm刻画图像边缘信息，使函数new(,)能够刻画真实的目标边界。

图4给出了2幅图像边缘停止函数的图像表示。图4(a)是含噪图像，在背景和目标区域，new(,)的值较小(图4(b))而new(,)的值接近1(图4(c))，表明作为边缘停止函数，new(,)受噪声干扰的程度小于(,)；图4(d)是边缘深度凹陷图像，(,)和new(,)在目标边界的值均接近0，但是new(,)对边缘细节有更多的表现(图4(f))。

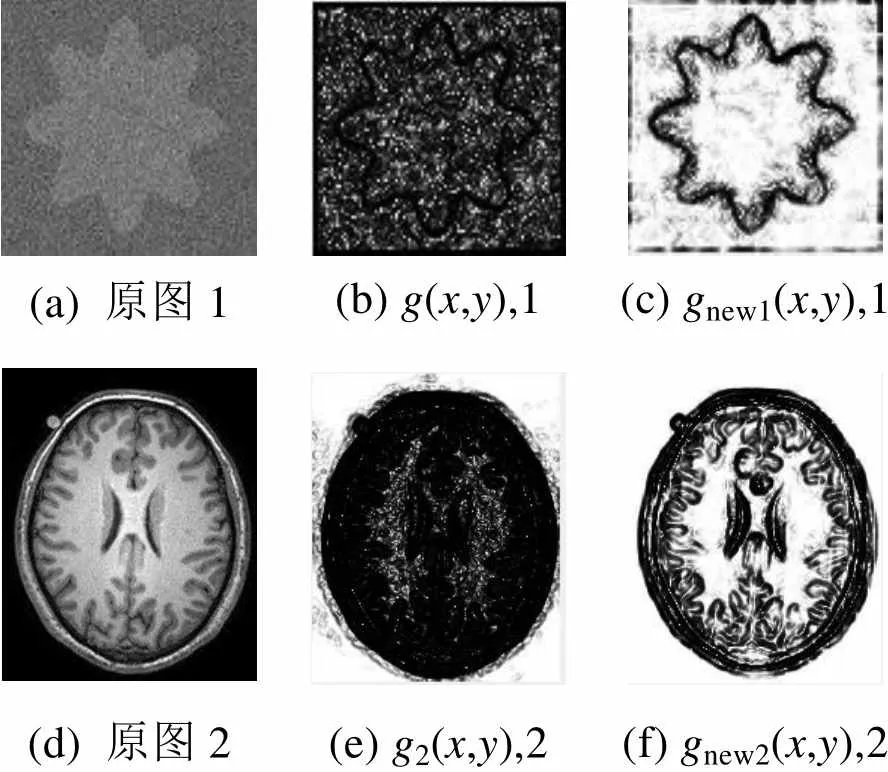
(a) 原图1(b) g(x,y),1(c) gnew1(x,y),1 (d) 原图2(e) g2(x,y),2(f) gnew2(x,y),2

3.3 自适应权重系数

图像的目标与背景区域分别记为I和I。为了克服DRLSE模型对初始轮廓的依赖性和对演化速度敏感的缺点，本文引入了基于图像信息的自适应权重系数

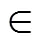
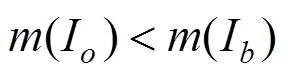
(2)new(,)的大小与图像梯度和小波系数梯度幅值有关。在图像光滑区域，|new(,)|较大，水平集快速演化以避免陷入虚假边缘；在目标边界处， |new(,)|较小，水平集平稳演化以避免出现边界泄漏；在含有噪声的区域，矩阵元素norm(,)较小使得水平集仍以较小的速度继续演化。权重系数能够根据图像信息自适应地调整大小，以保持水平集合理的演化速度。

将初始轮廓设置在与图像目标相交的位置，如图5所示。分别采用取固定值的DRLSE模型和new由式(9)定义的本文模型分割图像，由分割结果可以看出，DRLSE模型根据的符号引导水平集收缩或扩张演化，而图5(c)和5(f)证明了自适应权重系数new的有效性。

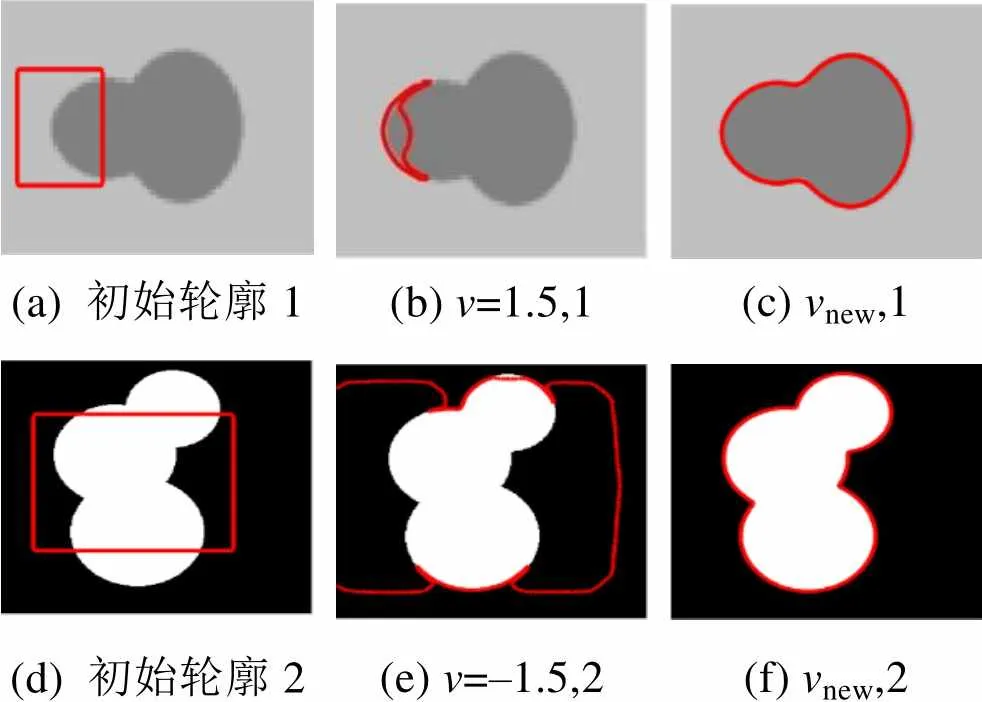
(a) 初始轮廓1(b)v=1.5,1(c)vnew,1 (d) 初始轮廓2(e)v=–1.5,2(f)vnew,2

3.4 改进的DRLSE水平集模型及数值实现

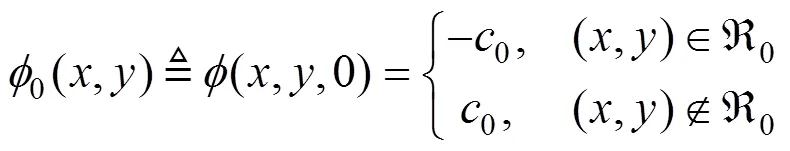
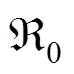
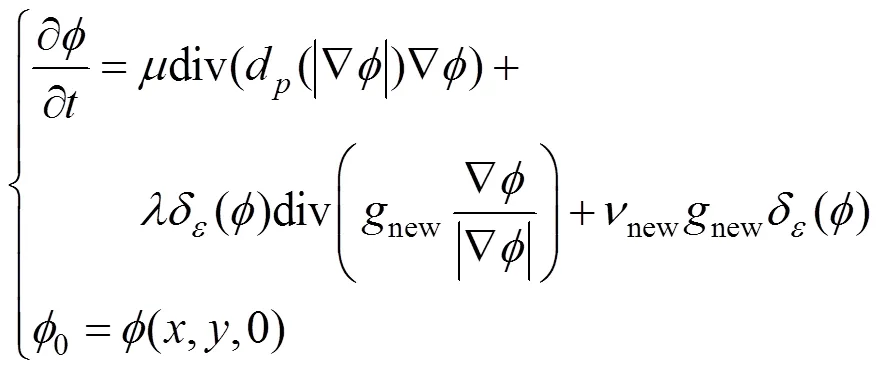
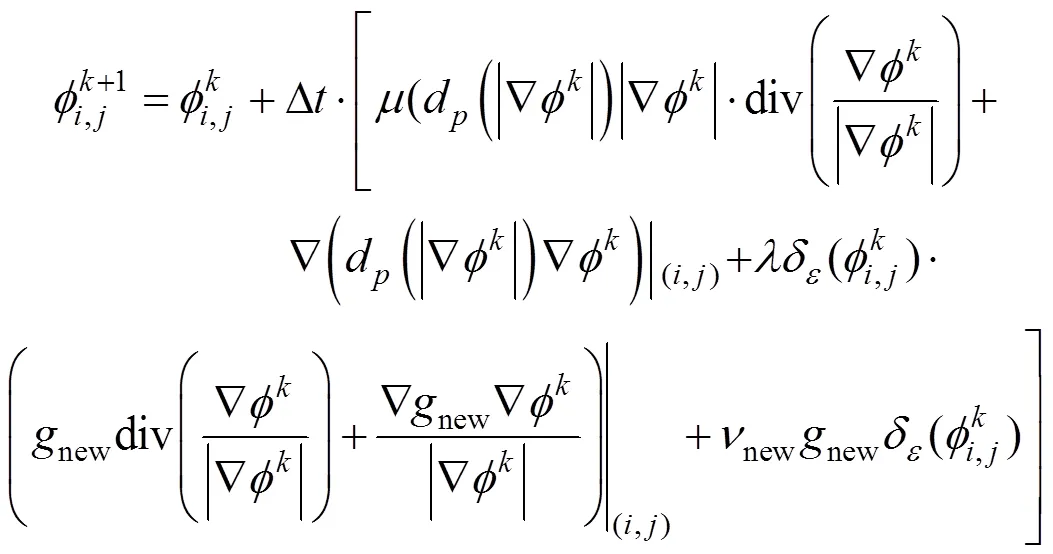
本文提出的改进DRLSE水平集模型的具体数值求解步骤如下：

步骤2.初始化水平集函数，设置参数0，计算初始轮廓内部灰度均值1和外部灰度均值2；

步骤3.将图像进行多层小波分解，对各尺度的小波细节系数进行阈值处理；

步骤4.计算边缘信息刻画矩阵norm，边缘停止函数new(,)和自适应权重系数new(,)；

步骤5.根据离散化的水平集演化方程式(11)演化水平集函数；

步骤6.判断水平集演化迭代次数是否完成，若完成，输出图像分割结果，否则转步骤5。

4 数值实验

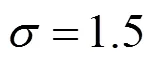
4.1 分割评价方法

为了定量分割和评价不同模型的分割质量，采用Jaccard相似(Jaccard Similarity, JS)系数来度量图像分割模型的精度[20]。Jaccard相似系数定义为

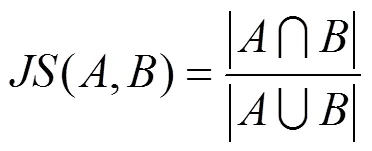
其中，为标准的分割结果；为待评价的分割结果。指标值越高则表明模型的分割效果越好。

4.2 对噪声的鲁棒性

为检验本文模型对含噪图像分割的有效性，设置DRLSE模型参数=3，本文模型参数1=3，2=8，迭代次数50，分割结果如图6所示。可以观察到：由于噪声的干扰，DRLSE模型中的演化曲线停止在虚假边缘处(图6(b))或者越过目标边界(图6(e))；本文模型在设定的迭代次数下成功分割出目标物体(图6(c)和图6(f))。

(a) 原图1(b) DRLSE 1(c) 本文模型2 (d) 原图2(e) DRLSE 2(f) 本文模型2

4.3 刻画目标边界的有效性

为检验本文模型检测目标物体复杂边界的有效性，选取如下边缘深度凹陷图像。设置DRLSE 模型参数=1.5，本文模型参数1=1.5，2=8，迭代次数30，图像分割结果如图7所示。可以观察到：DRLSE模型中的演化曲线不能收敛到目标物体深度凹陷的边界(图7(b))；本文模型则能够成功分割出图像的深度凹陷部分(图7(c))，并且能够捕捉到目标物体的真实边界(图7(f))。

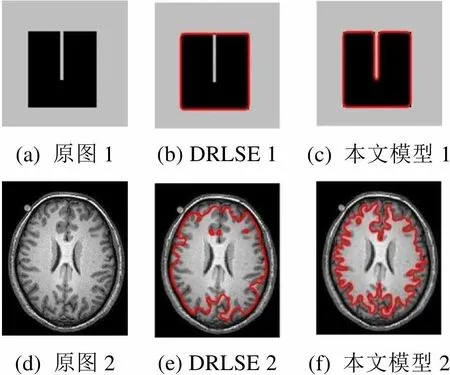
(a) 原图1(b) DRLSE 1(c) 本文模型1 (d) 原图2(e) DRLSE 2(f) 本文模型2

4.4 水平集演化的自适应性

为检验自适应权重系数new(,)的有效性，选取如下噪声图像。设置DRLSE模型参数=1.5，本文模型参数1=1.5，2=6，迭代次数分别为15和30。初始轮廓设置为包含目标、在目标内部和与目标相交3种情形，图像分割结果如图8所示。可以观察到：使用本文模型时，初始轮廓无论置于何处均能够经15次迭代后收敛到目标边界，如图8(d)所示；而使用DRLSE模型，只有初始轮廓与目标区域不相交并且需要经30次迭代才能完成对目标物体的分割(图8(c))。

(a)初始 轮廓(b) DRLSE,15(c) DRLSE,30(d)本文模 型,15

4.5 分割复杂图像的有效性

另外，检验本文模型对各类复杂图像的分割效果，并与DRLSE模型和文献[21]模型进行对比分析。选取高噪声图像(图9(a)~(b))，边缘深度凹陷图像(图9(c)~(d))以及遥感图像(图9(e)~(f))。设置DRLSE模型参数=1.5，文献[21]模型参数=3，本文模型参数1=1.5，2=8，图像分割结果如图9所示，对应的迭代次数、演化时间以及Jaccard相似系数分别见表1和表2。

(a) 原图1(a1) DRLSE,1(a2) 文献[21],1(a3) 本文,1 (b) 原图2(b1) DRLSE,2(b2) 文献[21],2(b3) 本文,2 (c) 原图3(c1) DRLSE,3(c2) 文献[21],3(c3) 本文,3 (d) 原图4(d1) DRLSE,4(d2) 文献[21],4(d3) 本文,4 (e) 原图5(e1) DRLSE,5(e2) 文献[21],5(e3) 本文,5 (f) 原图6(f1) DRLSE,6(f2) 文献[21],6(f3) 本文,6

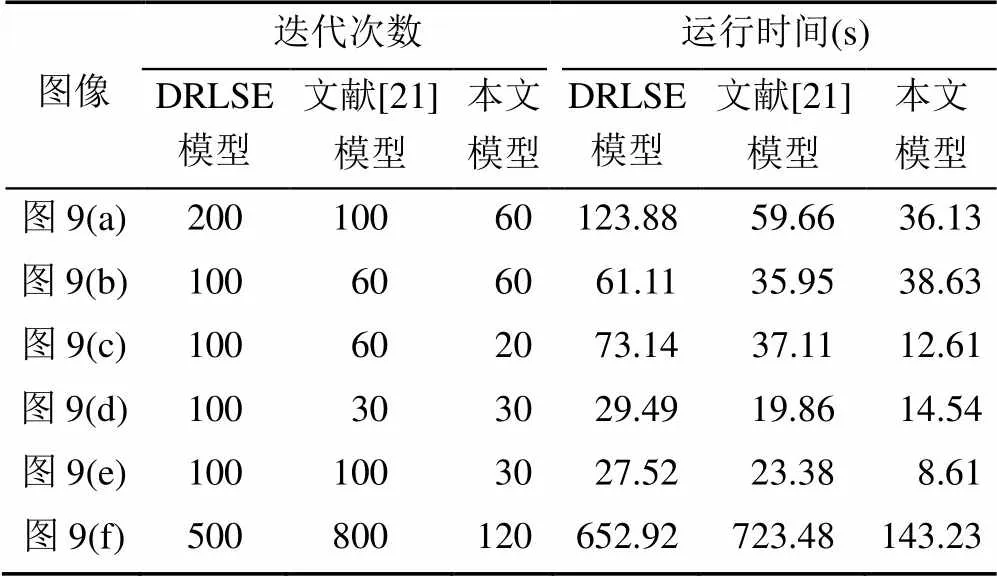
表1 不同模型的迭代次数与演化时间对比

表2 图9(a)~(d)采用不同模型分割的Jaccard相似系数

从图9可知，由于噪声的干扰以及局部熵块效应的影响，文献[21]模型没有对图9(b)和9(e)的目标区域进行精确地分割，如图9(b2)和9(e2)所示；图9(c)中，动物四肢的轮廓表现为图像的深度凹陷边缘，DRLSE模型和文献[21]模型均不能将动物的四肢准确分割出来，如图9(c1)~(c2)所示；对于灰度不均匀且多有凹陷区的遥感图像(图9(f))，文献[21]模型中的演化曲线即使经过800次迭代也不能完全收敛到目标物体的真实边界，如图9(f2)所示。

结合表1，对于图9中的所有图像，采用本文模型使用相对较少的迭代次数在较短的演化时间内均得到较为理想的分割结果。相比于DRLSE模型，本文模型的迭代次数平均减少了70%，演化时间平均减少了73.13%。再结合表2，本文模型的分割效果比其他两种模型更好。

5 结束语

本文针对DRLSE模型的不足，通过定义新的边缘停止函数和自适应权重系数，提出了改进的DRLSE水平集模型，并通过数值实验验证了改进模型及算法的有效性。相较于DRLSE模型，本文模型对噪声有更强的鲁棒性，对边缘信息的捕捉能力更好，分割图像的效率和精度也更高。

[1] OSHER S, SETHIAN J A. Fronts propagating with curvature dependent speed: Algorithms based on Hamilton-Jacobi formulations [J]. Journal of Computational Physics, 1988, 79(1): 12-49.

[2] HAN X, XU C, PRINCE J L. Topology preserving level set method for geometric deformable models [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(6): 755-768.

[3] SELLES V, CATT F, COLL T, et al. A geometric model for active contours in image processing [J]. Numerische Mathematik, 1993, 66(1): 1-31.

[4] MALLADI R, SETHIAN J A, VEMURI B C. Shape modeling with front propagation: A level set approach [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1995, 17(2): 158-175.

[5] LI C, XU C, GUI C, et al. Level set evolution without re-initialization: A new variational formulation [C]// Proceeding of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. New York: IEEE Press, 2005: 430-436.

[6] KASS M, WITKIN A, TERZOPOULOS D. Snakes: Active contours models [J]. International Journal of Computer Vision, 1988, 1(4): 321-331.

[7] XU C, PRINCE J L. Snakes, shapes and gradient vector flow [J]. IEEE Transactions on Image Processing, 1998, 7(3): 359-369.

[8] LIE J, TAI L X C. A variant of the level set method and applications to image segmentation [J]. Mathematics of Computation, 2006, 75(255): 1155-1175.

[9] CASELLES V, KIMMEL R, SAPIRO G. Geodesic active contours [J]. International Journal of Computer Vision, 1997, 22(1): 61-79.

[10] LI C, XU C, MEMBER S, et al. Distance regularized level set evolution and its application to image segmentation [J]. IEEE Transactions on Image Processing, 2010, 19(12): 3243-3254.

[11] LIU C, LIU W, XING W. An improved edge-based level set method combining local regional fitting information for noisy image segmentation [J]. Signal Processing, 2017, 130: 12-21.

[12] HE C J, LI M, ZHANG Y. Adaptive distance preserving level set evolution for image segmentation [J]. Journal of Software, 2009, 19(12): 3161-3169.

[13] LIU C, LIU W, XING W. A weighted edge-based level set method based on multi-local statistical information for noisy image segmentation [J]. Journal of Visual Communication and Image Representation, 2019, 59(1): 89-107.

[14] 谢杰成, 张大力, 徐文立. 小波图象去噪综述[J]. 中国图象图形学报, 2002, 7(3): 209-217.

[15] 付金明, 羿旭明. 基于小波多分辨率分析和改进窄带法的C-V水平集图像分割模型[J]. 数学杂志, 2016, 36(4): 867-874.

[16] 杨志巧, 羿旭明. 基于小波边缘刻画与LBF水平集变分模型的图像分割[J]. 数学杂志, 2019, 39(1): 87-96.

[17] OSHER S, FEDKIW R, PIECHOR K. Level set methods and dynamic implicit surfaces [J]. Applied Mechanics Reviews, 2004, 57(3): 15-273.

[18] 王大凯, 侯榆青, 彭进业. 图像处理的偏微分方程方法[M]. 北京: 科学出版社, 2008: 1-224.

[19] 相瑞, 王力, 何庆, 等. 小波变换与偏微分方程的图像去噪算法[J]. 通信技术, 2017, 50(1): 30-37.

[20] 冀珂, 羿旭明. 基于变动权值的混合水平集图像分割模型[J]. 图学学报, 2017, 38(6): 831-836.

[21] 张梦梦, 张泾周, 周三平, 等. 基于局部熵的边界与区域水平集图像分割模型[J]. 系统工程与电子技术, 2016, 38(12): 2884-2888.

An Improved Method for Image Segmentation Based on DRLSE Level Set

WEI Chen-chen, YI Xu-ming

(School of Mathematics and Statistics, Wuhan University, Wuhan Hubei 430072, China)

Aiming at the fact that the DRLSE level set model is inadequately sensitive to noise and dependent on the initial contour and slow evolution we used wavelet transform and wavelet threshold denoising methods. A new edge stop function and adaptive weight coefficient based on image information are defined by constructing the edge characterization matrix which is not sensitive to noise. An improved DRLSE level set image segmentation model is thus obtained. The finite difference method is employed to solve the model, and Jaccard similarity is used as the quantitative analysis method of evaluation model. The numerical results show that the improved model and algorithm are effective for image segmentation, overcoming the limitation of DRLSE level set model and dividing the noisy image and defining the initial contour position, which improve the computational efficiency and image segmentation precision of the DRLSE level set model.

image segmentation; DRLSE level set; edge stop function; adaptive

TP 391

10.11996/JG.j.2095-302X.2019050885

A

2095-302X(2019)05-0885-07

2019-04-29；

22019-07-08

国家自然科学基金面上项目(11671307)

魏晨晨(1995-)，女，安徽宿州人，硕士研究生。主要研究方向为图形图像处理。E-mail：783424700@qq.com

羿旭明(1964-)，男，湖南澧县人，教授，博士。主要研究方向为小波分析理论及其应用、图像处理。E-mail：247960864@qq.com