解决有界磁场中带电粒子运动问题的“三板斧”

(江苏省高淳高级中学，江苏 南京 221300)

带电粒子在有界磁场中的运动问题能够全面考查学生的物理知识和应用数学解决物理问题的能力，往往作为高考的必考题和压轴题。这类问题其实也有章可循，除了掌握定圆心、找半径和三角关系等基本方法外，还可以根据带电粒子的入射点、入射方向和入射速度关系，利用“三板斧”，以不变应万变。

图1

通过对比不难发现：在带电粒子的入射点、入射方向和入射速度三个变量中，往往是某一个发生变化，其他两个不变，可以采用控制变量法来研究，分成三类：(1) 入射点平移，入射方向和速度不变(半径不变)，在无边界磁场中据此画圆(如图1)，像一个圆沿某方向平移形成的轨迹，称之为“平移圆”法；(2) 入射速度大小变化(半径变化)，入射点和入射方向不变，在无边界磁场中据此画圆(如图2)，像一个圆沿某方向逐渐扩大和缩小形成的轨迹，称之为“缩放圆”法；(3) 入射方向变化(半径变化)，入射点和入射速度大小不变(半径不变)，在无边界磁场中据此画圆(如图3)，像一个圆沿某方向逐渐旋转形成的轨迹，称之为“旋转圆”法。利用以上解决带电粒子在有界磁场运动的“三板斧”，可以很好地解决问题，有效降低理解题的思维难度，下文以例题的形式分别展示三种方法的应用。

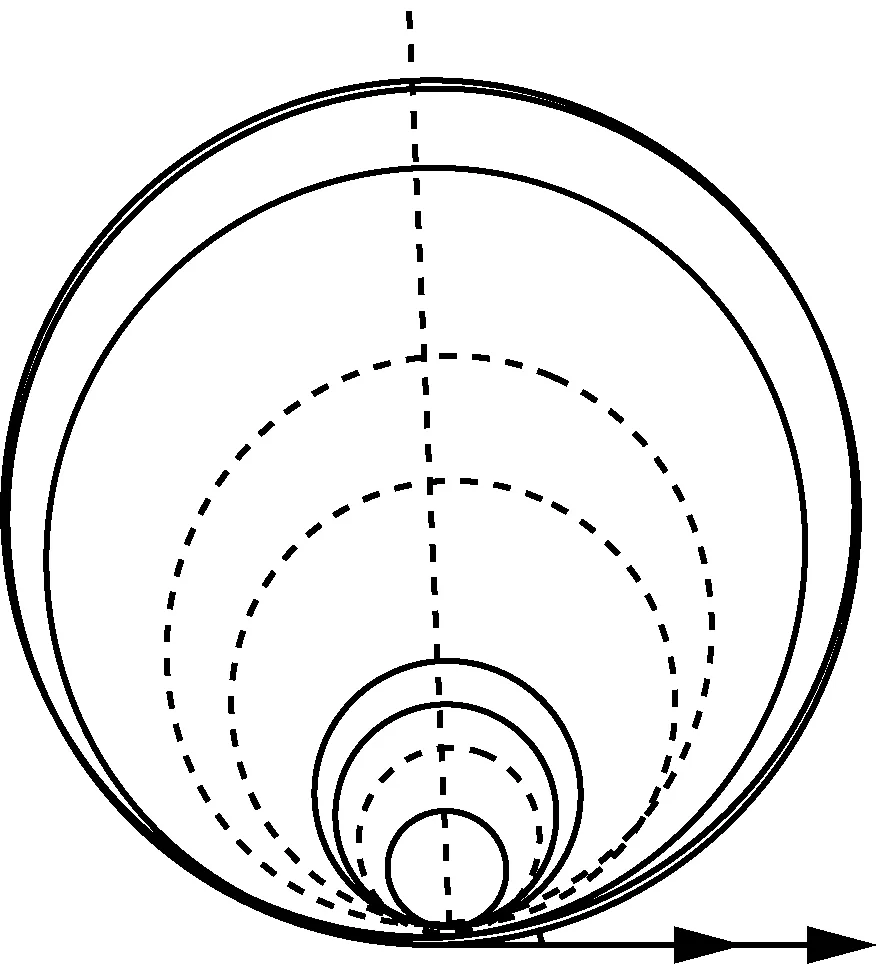
图2

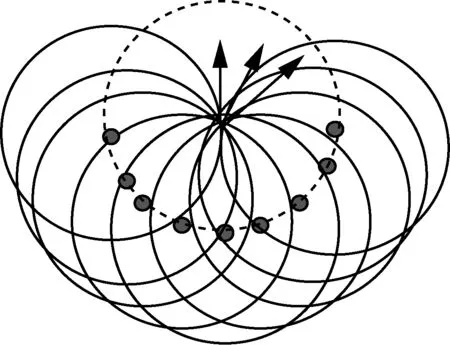
图3

1 “平移圆”的应用

例1：一台质谱仪的工作原理如图4所示，大量的离子飘入电压为U0的加速电场，其初速度几乎为0，经过加速后，通过宽为L的狭缝MN沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中，最后打到照相底片上。已知离子的电荷量为+q，质量为m，图中虚线为经过狭缝左、右边界M、N的离子的运动轨迹。不考虑离子间的相互作用。在图中用斜线标出磁场中离子经过的区域，并求该区域最窄处的宽度d。

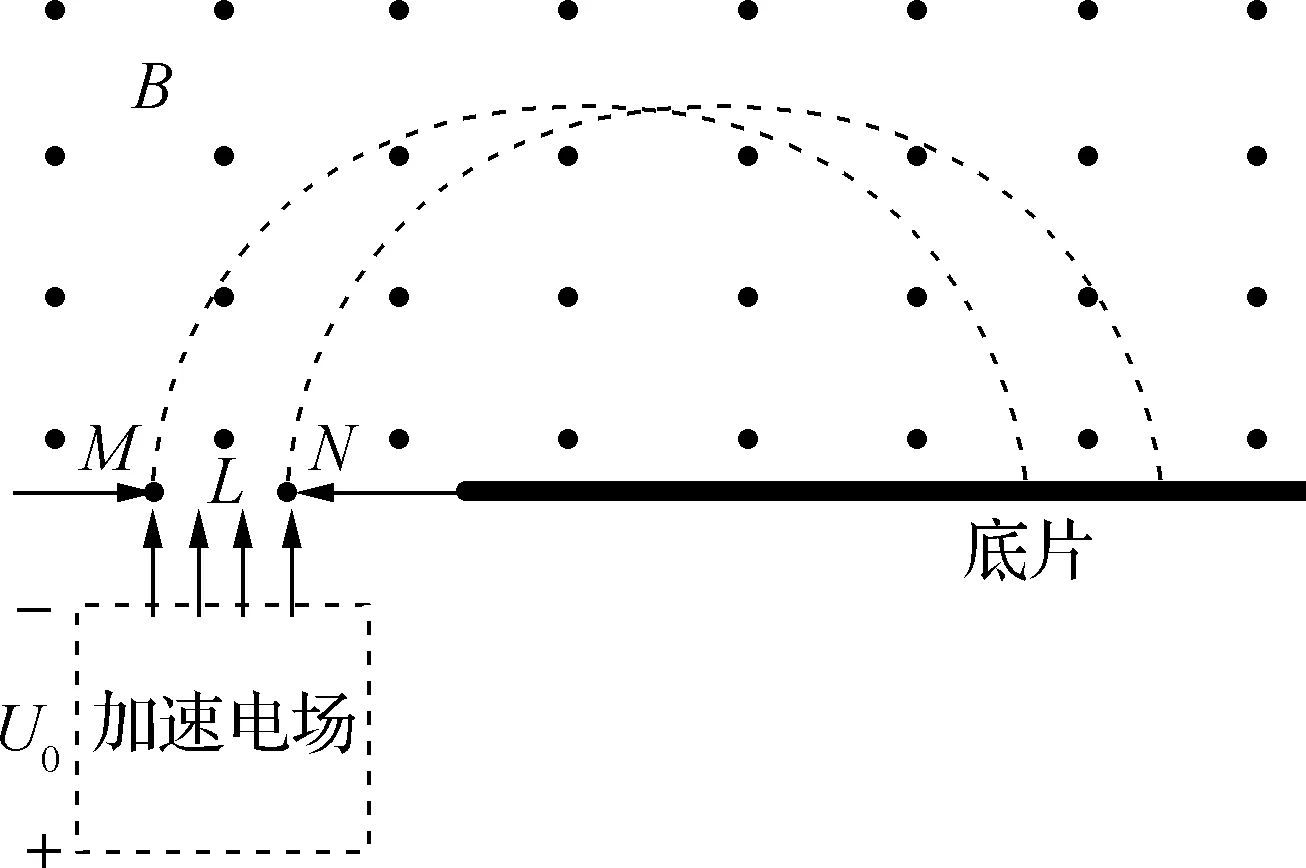
图4

解析：大量粒子的入射速度大小和方向不变，只有入射点不同，符合“平移圆”的特点，然后按照平移圆规律画出粒子的轨迹(如图5)，据图5可很快找到区域最窄处，再利用三角关系求解，解决本题的关键是画出粒子的运动“平移圆”轨迹。

图5

2 “缩放圆”的应用

例2：一足够长的矩形区域abcd内存在磁感应强度为B、方向垂直纸面向里的匀强磁场，矩形区域的左边界ad宽为L，现从ad中点O垂直于磁场射入一带电粒子，速度大小为v0，方向与ad边夹角为30°(如图6)。已知粒子带正电，电荷量为q，质量为m，不计重力，要使粒子能从ab边射出磁场，求v0的取值范围。

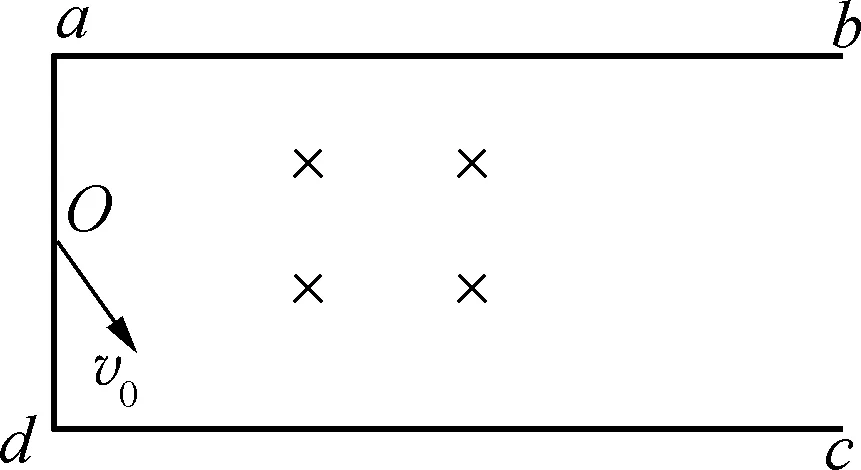
图6

解析：大量粒子的入射点和入射方向不变，只有入射速度大小不同，符合“缩放圆”的特点，然后按照缩放圆规律画出粒子的轨迹(如图7)，据图7可很快找到轨迹与ab和cd相切的临界情况，再利用三角关系求解，解决本题的关键是画出粒子运动的“缩放圆”轨迹。

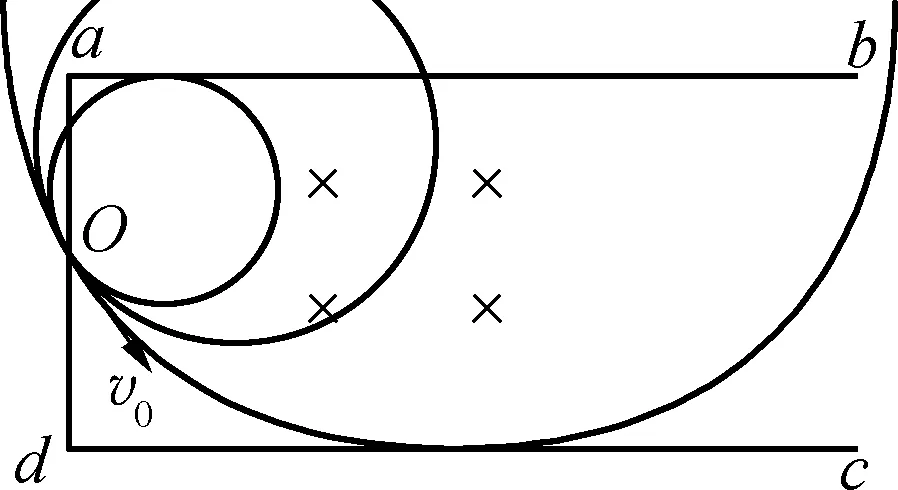
图7

3 “旋转圆”的应用

图8

(1) 最后离开磁场的粒子从粒子源射出时速度的大小；

(2) 速度方向与y轴正方向的夹角。

解析：大量粒子的入射速度大小和入射点不变，只有入射方向不同，符合“旋转圆”的特点，按照旋转圆规律画出粒子的轨迹(如图9)，据图9可以很快找到运动轨迹与上边界相切是极值，再利用三角关系求解，解决本题的关键是画出粒子运动的“旋转圆”轨迹。

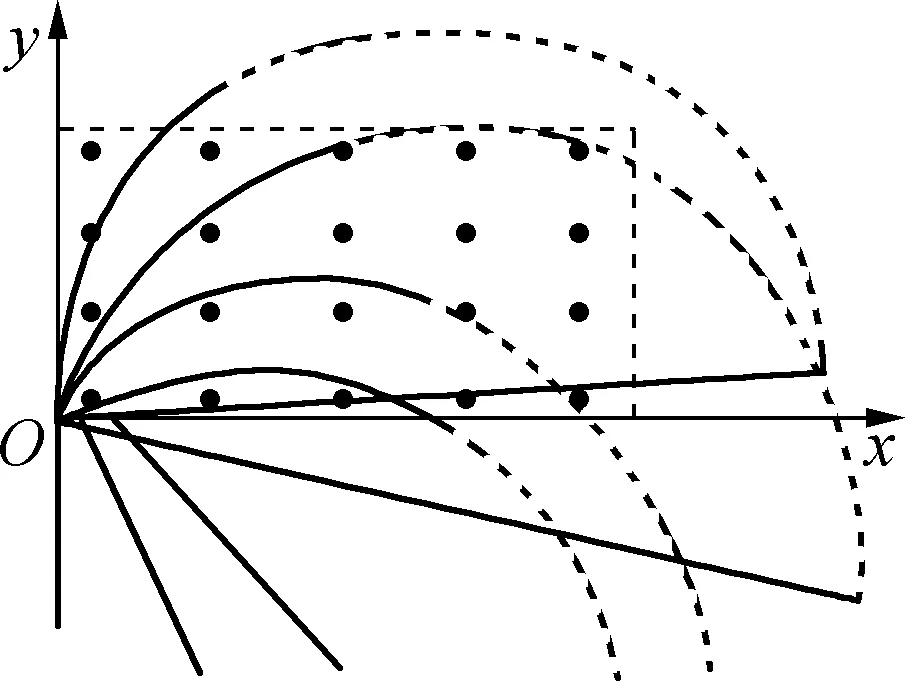
图9

在教学中教给学生解决此类问题的“三板斧”后，可以有效突破带电粒子在有界磁场中运动的难点。根据带电粒子的入射点、入射方向和入射速度三个变量的特点，快速从“平移圆”“缩放圆”和“旋转圆”中确定解题方向，大大降低了问题的难度，有助于学生深入理解问题的本质。