混合kNN算法在2型糖尿病预测诊断中的研究

崔波 朱晓军

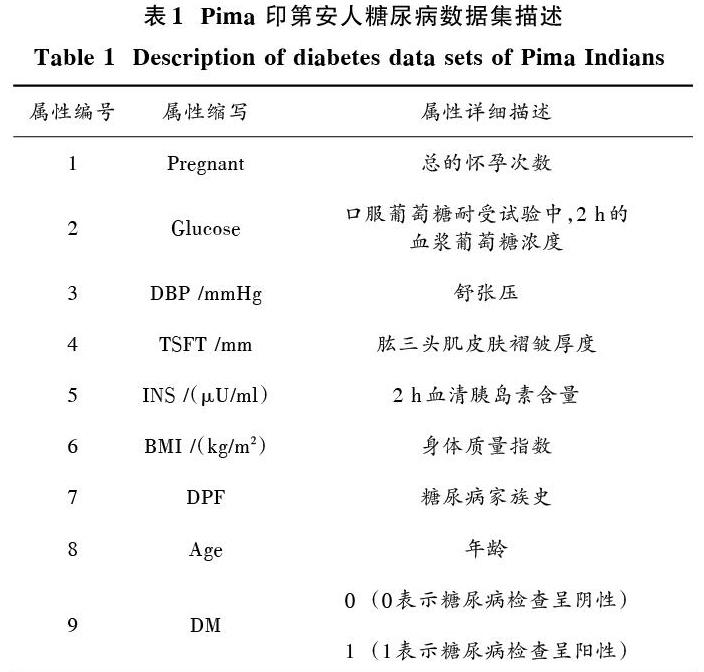
摘  要： 2型糖尿病（T2DM）原始医疗数据具有广维度、多噪声、强耦合、非线性等特点。传统的kNN算法不能很好地利用全局信息，对异常值也不敏感，并且算法中的近邻值k以及权重的确定对于实验结果有很明显的影响，因此，提出一种混合kNN算法（IPCA?kNN）预测诊断2型糖尿病患者的新型预测模型。采用ISODATA算法对离散点进行剔除，数据集中的缺失值使用随机加权热卡（BB?Hotdeck）算法进行插补;构造kNN分类器时使用主成分分析（PCA）对每个属性赋不同权重，对于k值的确定使用交叉验证中的K?fold Cross Validation（K?CV）算法，通过准确度、敏感度和特异度验证所提模型有效。

关键词： 2型糖尿病; 预测诊断; 混合kNN; 数据处理; 仿真实验; 结果分析

中图分类号： TN912?34; TP202                       文献标识码： A                  文章编号： 1004?373X（2019）20?0164?05

Hybrid kNN algorithm for predictive diagnosis of type 2 diabetes

CUI Bo， ZHU Xiaojun

（Taiyuan University of Technology， Taiyuan 030024， China）

Abstract： The original medical data of type 2 diabetes mellitus （T2DM） has some characteristics， such as wide dimensionality， multi?noise， strong coupling， nonlinearity. The traditional k?Nearest Neighbor （kNN） algorithm can't make good use of the global information and insensitivity to outliers， and the determination of the nearest neighbor value k and the weight in the algorithm has obvious influence on the experimental results. Therefore， a new predictive model of hybrid kNN （IPCA?kNN） algorithm is proposed to predict and diagnose the patients with T2DM. The iterative self?organized data analysis （ISODATA） is used to eliminate the discrete points. The missing values in the data set are interpolated by means of Bayesian Bootstrap?Hotdeck （BB?Hotdeck） algorithm. When constructing the kNN classifier， the principal component analysis （PCA） is used to assign different weights to each attribute， the K?fold cross validation （K?CV） in cross?validation is used to determine the value of K. The validity of the model is verified by accuracy， sensitivity and specificity.

Keywords： Type 2 diabetes; predictive diagnosis; hybrid kNN; data processing; simulation experiment; result analysis

0  引  言

来自国际糖尿病联盟（IDF）的资料显示，2017年全球共有糖尿病患者4.25亿，预计到2040年这一数字将上升到6.42亿，糖尿病已成为新世纪全球最大的人类健康危机之一[1]。而中国糖尿病患者数量排第一，其中2型糖尿病约占所有确诊的糖尿病成人病例的90%～95%。目前，大多数分类、鉴定和诊断治疗都基于化学和物理测试，从这些结果中获得推论来预测T2DM。但是，由于用于测试的各种参数的不确定性，会使预测产生错误，反而可能降低疾病控制和治愈的可能性。根据N. Esfandiari等人提出的定义 “从医学数据中提取隐藏的、具有潜在价值的和新颖的信息，以提高准确性，减少时间和成本，构建以健康保护为目的的决策支持系统”[2]。因此，基于机器学习和数据挖掘的新型预测模型的构建对于2型糖尿病患者早期诊断并随后提供适当的治疗是尤为重要的。

2008年，K. Polat等人已证明kNN是一种思想简单但十分有效的分类技术，可以用于糖尿病的分类诊断，并且达到了71.9%的准确度[3]。在此基础上，2013年，Y. A. Christobel等人使用平均插补方法取代缺失值，提出了一种新的基于类的k最近邻（CkNN）方法，该方法对糖尿病数据分类准确度为78.16%，但是该方法没有考虑kNN对离群点不敏感、数据不平衡等缺点[4]。仲媛等人提出了利用SVM来确定特征的权重，即基于特征加权算法FWkNN（Feature Weighted kNN），对准确度有一定的提升，但是无法很好地解决离散点对于预测准确度的影响。2016年，曾勇等人提出了基于BP神经网络的自适应伪最近邻分类，考虑BP神经网络的输入值时，选择了计算待测试数据点和样本集中每一类别样本集中的各个近邻的距离值[5]。2017年，M. Maniruzzaman等人使用高斯过程分类（GPC）[6]，预测诊断的准确度为81.97%。本文主要针对kNN算法对离群点不敏感、数据不平衡、如何合理选择k值及确定权重不足提出改进方法，设计一种混合kNN算法预测诊断2型糖尿病患者的新型预测模型，即IPCA?kNN。预测诊断模型使用加利福尼亚大学欧文分校机器学习数据库知识库（UC Irvine Machine Learning Repository）中的Pima印第安人糖尿病数据集（Pima Indians Diabetes Dataset），使用准确度（ACC）、敏感度（SE）、特异度（SP），综合评估了本研究所提出的混合IPCA?kNN分类模型的表现。

1  相关算法介绍

1.1  迭代自组织数据分析法

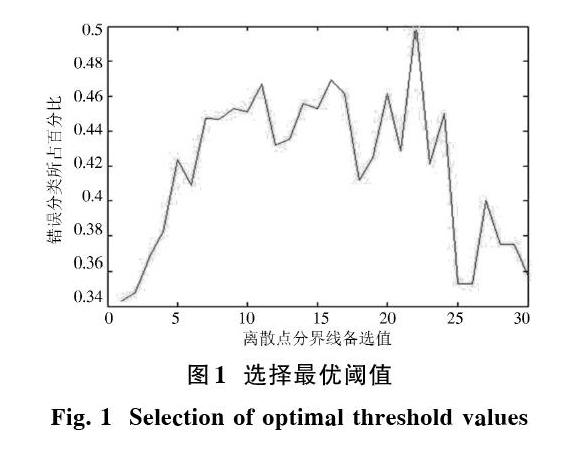
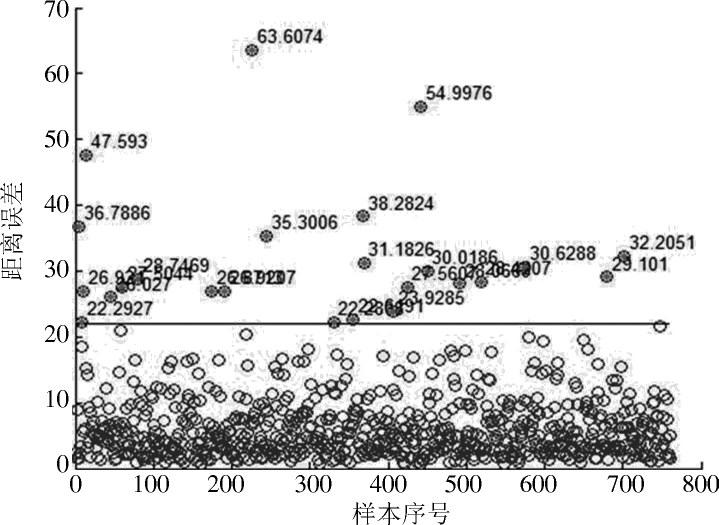
常用的K?means算法最早由MacQueen在1967年提出，属于无监督聚类方法，无监督的数据聚类是一个任务，将点分配给聚类，同时估计聚类的位置和形状[7]。本文使用欧几里德距离测量，改进的K?means算法——迭代自组织数据分析法（ISODATA）算法可以设定指标参数决定是否进行“合并”或“分裂”，具有自动调节最优类别数k的能力，用于检测数据集中离散点，准确度较高。详细过程如下：

1） 初始化预期聚类中心、类中最少样本数、每个聚类中样本距离分布的标准差、两聚类中心的最小距离、每次迭代运算中可合并的最多对数以及迭代运算次数;

2） 计算各类中样本的距离指标函数;

3） 判断各聚类域中的样本数目是否符合初始参数的设定，调整聚类中心数目;

4） 修正各个聚类中心并计算每个聚类域中的样本与各个聚类中心间的平均距离以及全部样本与其对应的距离中心的总平均距离;

5） 判断分裂、合并以及迭代运算，重新确定聚类中心数;

6） 重复迭代，若需要改变初始参数，则转到步骤1）;若不需要改变则转步骤2）;若为最后一次迭代，则结束。

1.2  随机加权热卡（BB?Hotdeck）算法

热卡填充法（Hotdeck）插补是随机地从回答样本中抽取回答单元来替代缺失数据，而随机加权通过给每个试验样本随机加权进行分布参数和参数区间估计，而不需要了解总体分布[8]。BB?Hotdeck算法描述如下：

1） 根据分类变量将数据集分为两层即0和1，将每层中没有缺失数据的行（row）定义为[Ycom]，而有缺失数据的行定义为[Ymiss];

2） 利用随机加权法（BB）从[Ycom]中随机抽取某一行（或某几行）来替换缺失行，便得到一个完整的数据集，从而可以用标准的统计方法来分析该数据集;

3） 重复上述步骤n次，并对n次分析结果进行综合分析。

1.3  主成分分析（PCA）

数据集中的每个属性（指标）对于预测诊断都有其意义，但是各个指标的贡献度未必相同，保留原始数据特征采用PCA对每个指标进行加权，加权后的数据再使用kNN进行分类。PCA算法的原理如下：

1）输入训练数据集 [D=x1，y1，x2，y2，…，][xn，yn]训练集为[Dtr]，测试集为[Dte]，其中[xi∈D]为实例的特征向量，[yi∈Dc1，c2，…，ck]为实例的类别，i=1，2，…，n。

2） 取训练数据集构造测试样本矩阵 [X=Dtr= xT1xT2?xTn= x11x12…x1px21x22…x2p????xn1xn2…xnp]，其中，[xij]表示第i组样本数据中的第j个变量的值。

3） 对训练样本X进行变换得[Y=yijn×p]，其中， [yij= xij，  对正指标-xij，对逆指标]。

4） 对Y做标准化变换得标准化矩阵[Z=zT1zT2?zTn= z11z12…z1pz21z22…z2p????zn1zn2…znp]，其中，[zij= yij-yjsj]，[yj]，[sj]分别为Y阵中第j列的均值和标准值。

5） 计算标准化矩阵Z的样本相关系数阵 [R= [rij]p×p=ZTZn-1]。

6） 计算特征值 [R-λIp=0] ， 解得p个特征值[λ1≥λ2≥…≥λp≥0]。

7） 求解[Rb= λjb]，得单位向量[b0j=bj||bj||]。

8） 计算[zi= （zi1，zi2，…，zip）T]的m个主成分分量[uij=zTib0j，j=1，2，…，m] ，得到决策矩阵[U=uT1uT2?uTn= u11u12…u1mu21u22…u2m????up1up2…upm]，其中，[ui]为第i个变量的主成分向量。

9） 主成分模型如下：

[F1= u11w1+u21w2+…+uL1wLF2= u12w1+u22w2+…+uL2wL?                            ? Fm= u1mw1+u2mw2+…+uLmwL]

式中：[F1，F2，…，Fm]为分析后得到的m个主成分;[uij]为决策矩阵中系数。

10） [uij= fijλi，j=1，2，…，m]，其中[fij]为初始因子载荷。

11） 构建综合评价函数。

[FZ=j=1m（λjk）Fj= a1w1+a2w2+…+aLwL，         k= λ1+λ2+…+λm]

式中，[a1，a2，…，aL]，即指标[w1，w2，…，wL]在主成分中的综合重要度。

12） [VZi= j=1Laj]，可得各指标的权重为[ωi=VZii=1hVZi]。

1.4  k最近邻算法（kNN）

kNN算法由于无需估计参数、适合多类交叉或重叠分类问题、易于实现等优点被广泛使用各个领域。kNN算法原理如下：

1） 将各指标权重赋予训练集和测试集，得到新的数据集[L=ωix1，y1，ω2x2，y2，…，ωnxn，yn];

2） 计算测试数据与各个训练数据之间的距离[d（x，y）]，距离公式选择欧氏距离，并对这些距离从小到大排序，[d（x，y）=k=1nxk-yk2] ;

由图4和表3可以看出，本文提出的IPCA?kNN新型2型糖尿病预测诊断模型，对于PID测试集准确度达到91.54%，敏感度达到90.43%，特异度达到94.31%，分类的准确度高于其他部分分类算法，对于2型糖尿病的预测诊断具有较好的效果，可以作为一种新的预测模型加以利用。

4  结  语

糖尿病已成为影响全球居民健康的主要慢性非传染病之一，其中2型糖尿病的早??期诊断对预防及治疗至关重要。本文提出一种混合kNN的预测诊断模型，即IPCA?kNN，用于分类识别T2DM患者。本文提出的模型好处之一是避免了删除过多的原始数据，确保了实验数据的高质量，在此基础上解决了kNN离散点敏感、权重无法确定等不足;另一点是，模型使用灵敏度、特异度和准确度共同来评价模型分类性能，通过与其他方法比较，结果表明本研究所提出的方法性能优于其他算法，可以作为预测诊断T2DM的新型预测模型。

T2DM的预测诊断是一个复杂的问题，因此，在未来的研究中，应该再更新更完整的糖尿病数据集对本文的新型预测诊断模型进行测试。其次，可以利用Map?Reduce编程技术将本文提出的IPCA?kNN算法并行化，提高分类器的效率。

注：本文通讯作者为朱晓军。

参考文献

[1] 李咏梅.糖尿病的流行现状与预防[J].心理医生，2016，22 （31）：266?267.

LI Yongmei. Prevalence and prevention of diabetes [J]. Psychologist， 2016， 22（31）： 266?267.

[2] ESFANDIARI N， BABAVALIAN M R， MOGHADAM A M E， et al. Knowledge discovery in medicine： current issue and future trend [J]. Expert systems with applications， 2014， 41（9）： 4434?4463.

[3] POLAT K， SALIH G?NE， ARSLAN A. A cascade learning system for classification of diabetes disease： generalized discriminant analysis and least square support vector machine [J]. Expert systems with applications， 2008， 34（1）： 482?487.

[4] CHRISTOBEL Y A， SIVAPRAKASAM P. A new classwise k nearest neighbor （CKNN） method for the classification of diabetes dataset [J]. International journal of engineering & advanced technology， 2013， 2（3）： 396?400.

[5] 曾勇，舒欢，胡江平，等.基于BP神经网络的自适应伪最近邻分类[J].电子与信息学报，2016，38（11）：2774?2779.

ZENG Yong， SHU Huan， HU Jiangping， et al. Adaptive pseudo nearest neighbor classification based on BP neural network [J]. Journal of electronics & information technology， 2016， 38（11）： 2774?2779.

[6] MANIRUZZAMAN M， KUMAR N， MENHAZUL ABEDIN M， et al. Comparative approaches for classification of diabetes mellitus data： machine learning paradigm [J]. Computer methods and programs in biomedicine， 2017， 152： 23?34.

[7] ZHANG J Y， PENG L Q， ZHAO X X， et al. Robust data clustering by learning multi?metric Lq?norm distances [J]. Expert systems with applications， 2012， 39（1）： 335?349.

[8] 万让鑫，吴西良.基于Bayesian Bootstrap小样本产品性能可靠性评估[J].信息技术，2012（5）：174?176.

WAN Rangxin， WU Xiliang. Performance reliability assessment based on Bayesian Bootstrap method [J]. Information technology， 2012（5）： 174?176.

[9] 周志华.机器学习[M].北京：清华大学出版社，2016.

ZHOU Zhihua. Machine learning [M]. Beijing： Tsinghua University Press， 2016.

[10] HAN Jiawei， KAMBER M. Data mining concepts and techniques [M]. Waltham： Morgan Kaufmann Publishers， 2012.

[11] BOZKURT M R， YURTAY N， YILMAZ Z， et al. Comparison of different methods for determining diabetes [J]. Turkish journal of electrical engineering and computer sciences， 2014， 22（4）： 1044?1055.

[12] CHRISTOBEL Y A， SIVAPRAKASAM P. A new classwise k nearest neighbor （CKNN） method for the classification of diabetes dataset [J]. International journal of engineering & advanced technology， 2013， 2（3）： 396?400.