莱维飞行优化果蝇算法在光伏MPPT中的研究

赵其浩 李田泽 邵泰衡 吴繁言 王坦坦

摘  要： 实际工程中光伏阵列因局部遮挡引起局部阴影，造成输出的PU曲线呈现多峰值现象，传统方法进行最大功率点跟踪时，在跟踪精度、速度和最大功率点处振荡性都存在不足。为解决这些不足，在果蝇算法对多峰函数寻找最优解速度快的基础上，提出一种莱维飞行优化果蝇算法（LF?FOA）的光伏最大功率点跟踪策略。该方法以果蝇算法为主体，使用莱维飞行与果蝇算法相结合，增加其全局搜索能力，同时引入最劣解对果蝇运动步长进行修改，改进后的算法使果蝇以大小步长进行搜索，搜索的范围更加均匀，避免陷入局部寻优。通过函数仿真测试与Matlab/Simulink建模仿真，证明了LF?FOA算法能够逃离局部寻优，寻优时速度更快，精度更高，最大功率点处的振荡性更小。

关键词： 光伏阵列; 多峰值; 最大功率点跟踪; 莱维飞行; 果蝇算法; 最劣解

中图分类号： TN911?34; TP301.6                     文献标识码： A                  文章编号： 1004?373X（2019）20?0076?05

Research on Levy flight optimization Drosophila algorithm in photovoltaic MPPT

ZHAO Qihao， LI Tianze， SHAO Taiheng， WU Fanyan， WANG Tantan

（School of Electrical and Electronic Engineering， Shandong University of Technology， Zibo 255049， China）

Abstract： In practical projects， the multi?peak phenomenon appears in the output PU curves of photovoltaic arrays due to local shadows caused by partial occlusion. Common methods have some shortcomings in tracking accuracy， speed and oscillation at the maximum power point. To overcome these shortcomings， based on the fast searching speed for the optimal solution of multimodal function by the Drosophila algorithm， a photovoltaic maximum power point tracking strategy for the LF?FOA is proposed， which takes the Drosophila algorithm as the main body and combines the LV flight with the Drosophila algorithm to increase its global searching ability. When the worst solution is introduced to modify the movement step size of Drosophila melanogaster， the improved algorithm conducts the Drosophila melanogaster search with the big and small step sizes， which makes the search scope more uniform and avoids falling into local optimization. The results of function simulation test and MATLAB / Simulink modeling simulation prove that LF?FOA algorithm can escape from local optimization， and has faster optimization speed， higher precision and less oscillating at maximum power.

Keywords： photovoltaic array; multi?peak; maximum power point tracking; Levy flight; Drosophila algorithm; worst solution

随着石油、煤等传统能源的枯竭，世界各国对新型环保能源的开发和利用越来越重视。太阳能作为清洁、可再生能源，已成为各国重点关注的对象[1]。太阳能发电作为太阳能利用的主要形式，其存在转化效率较低的缺点。为提升光伏发电的转化效率，降低成本，必须对光伏系统进行最大功率点跟踪（MPPT）[2]。

针对最大功率点跟踪的研究，传统恒定电压法进行跟踪时，收敛精度和速度较差[3]。粒子群算法作为常用MPPT智能算法，其参数比较多，取值设置比较繁琐，同时搜索范围大，寻找最大功率点较慢，并且搜索随机，震荡性比较大[4?6]。

果蝇优化算法是近年来提出的一种新型智能算法，目前果蝇算法在数据挖掘、求解数学函数极值等很多领域得到应用[7?8]。本文在原始果蝇算法对多峰函数寻找最优解速度快、设置参数少的基础上，使用莱维飞行优化果蝇算法，同时在优化中引进最劣解，并将其首次应用到MPPT中，改进后的算法提升了收敛速度和寻优精度。通过仿真验证了算法的优越性，并与常用的扰动观察法在阴影条件下进行仿真对比，证明了本文算法的有效性。

1  阴影下光伏电池建模及输出特性

1.1  阴影下光伏电池建模

本文采用文献[9]中光伏电池的修正新模型，在光照相同的情况下，其数学模型为：

式中：I为光伏阵列输出电流;U为光伏阵列输出电压;ISC为短路电流;UOC为开路电压;C1和C2为修正参数;NS为串联阵列中的光伏电池个数;NP为串联阵列的并联个数。

在实际工程中，为了避免热斑效应，会对光伏电池并联单个二极管，如图1所示。

图1  两光伏组件串联结构图

當S1的光照强度大于S2时，S1产生的电流ISC1大于ISC2，此时并联旁路二极管导通，只有S1对外进行输出。随着外接负载电阻的增大，输出电流逐渐减小，当S2产生的电流与S1输出电流相同时，并联的旁路二极管处于阻断状态，此时S1和S2同时进行功率输出。根据旁路二极管的导通与关断状态，串联电池的电流特性可为：

1.2  阴影下光伏电池输出特性

采用三组件串联的形式在Matlab中进行仿真，对有阴影和无阴影情况进行测试。采用某型号的光伏电池，参数为：ISC=9.2 A，VOC=34.2 V，IM=7.95 A，VM=20 V。阴影1光照强度依次为1 000 W/m2，800 W/m2，600 W/m2;阴影2光照强度依次为800 W/m2，600 W/m2，400 W/m2;仿真结果如图2所示。

图2  无阴影及阴影下P?U曲线

2  莱维飞行优化果蝇算法的研究

2.1  果蝇算法

果蝇算法（FOA）是基于果蝇觅食行为推演出的一种能够进行全局寻优的最新方法。果蝇自身拥有较强的嗅觉和视觉能力，能够通过分辨空气中食物的各种气味，快速确定食物所处的大概位置，然后利用其视觉能力快速地飞行到食物所在的位置[10]。多个果蝇聚集到一起进行食物寻找就形成了一种群体智能寻优算法。

2.2  莱维飞行

莱维飞行是由法国的数学家Paul Lévy提出的一种概率分布。莱维飞行是一种随机游走的搜索方式，在搜索的过程中会出现较大的跃动，运动方向也会产生剧烈变化，这样就使得算法可以跳出局部寻优。莱维飞行的搜索路径采用文献[10]中的计算公式：

2.3  LF?FOA算法及运行流程

本文通过引入莱维飞行优化果蝇算法，在此基础上又引入最劣解对果蝇运动步长的变化进行修改，提出了一种基于莱维飞行优化果蝇算法（LF?FOA）的改进算法。

LF?FOA算法以果蝇算法为主体，先将果蝇算法与莱维飞行相结合，然后引入最劣解（Xworst，Yworst），最劣解为上一次迭代中出现的个体最差值，将其作为步长大小修改的参考量，可以使果蝇以大小步长飞向原本的小概率区域，使得搜索的范围更加的均匀。仿真结果表明了改进后效果更优秀，实现了更好的全局寻优。LF?FOA算法在光伏最大功率点跟踪流程如下：

1） 对果蝇位置的随机初始化，初始值Init U_axis，Init P_axis，同时设定种群规模Sizepop和最大迭代次数Maxgen。

2） 赋予果蝇个体利用嗅觉寻找食物的运动方向和运动距离。

3） 由于最优解的位置是未知的，先估计果蝇与原点的位置距离Dist，再计算味道浓度的判定值S，其取值为Dist的倒数。

4） 将上面求得的S代入味道浓度判断函数（Fitness Function）式（3）的功率表达式，求出每个味道浓度判定值对应的果蝇味道浓度（Smelli）。

5） 找出该果蝇群体中味道浓度最大和味道浓度最差的果蝇。

6） 保留味道浓度最优值与相对应的（U，P）的坐标，保留味道浓度最劣值和其对应的坐标，此时果蝇利用视觉能力飞往味道浓度最优位置。

7） 进入迭代寻优环节，利用式（12）替代式（6）对果蝇位置进行和运动距离进行修改，其中α的取值定为0.01。

8） 执行完步骤7）以后，执行步骤3）～步骤5）。然后将得到最优解与上一次进行对比，如果优于上一次则保存，并将对应的坐标保存，反之不保存。最劣解无需对比，直接以当前计算的值进行保存，并保存相应坐标用于下次迭代。

9） 重复执行步骤7）、步骤8），直至当前的迭代次数达到设定的Maxgen，或者达到目标函数的最优理论值，则完成算法迭代。

3  LF?FOA算法验证及仿真分析

3.1  LF?FOA算法可行性验证

为了验证优化后算法的性能，本文通过使用Sphere函数和Rastrigin函数两个典型函数对新的算法进行验证，函数形式如下：

1） Sphere函数

2） Rastrigin函数

图3展现了FOA在对Sphere函数进行寻优时，陷入了局部寻优，而LF?FOA算法则跳出局部寻优，对最优解寻求更准确;在对Rastrigin函数寻优时可以看出，LF?FOA算法寻优速度更快，在100次迭代时就找到最优解，而FOA要在200次迭代时才能寻找到最优解。由此可以看出LF?FOA算法在寻优速度上比FOA要快很多，同时可以跳出局部寻优。

图3  两函数适应度迭代寻优曲线

以上的函数验证可以得出LF?FOA算法性能优于FOA算法，证明了改进算法的可行性。

3.2  LF?FOA算法在MPPT中的仿真分析

为进一步证明本文方法的有效性，将本文所使用的LF?FOA算法与常用的扰动观察法在Matlab/Simulink中進行最大功率点跟踪的仿真，通过对比来验证本文算法的有效性。光伏电池组件采用三组件串联的形式，最大功率跟踪框图如图4所示。

图4  光伏最大功率跟踪框图

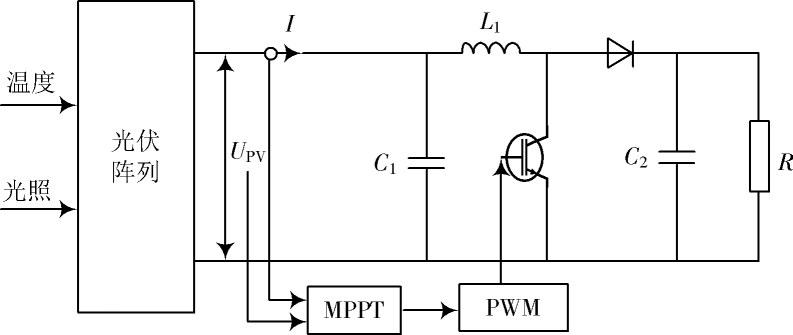
框图中包含：Boost电路、MPPT控制器、PWM、光伏阵列以及负载电阻。其中，C1为1 μF，C2为470 μF，L1为5 mH，仿真时间设定为1 s，光伏组件参数与第一节中相同。LF?FOA算法种群规模Sizepop设置为100，最大迭代次数Maxgen设置为50。

在阴影1的情况下，用扰动观察法和本文方法对最大功率点进行跟踪，结果如图5所示。

图5  阴影1下P&O与LF?FOA的MPPT仿真对比

图5为光照处于阴影1的恒定情况下的仿真曲线，温度为25 ℃，光伏整列输出功率为353.70 W。从图5中可以看出，初始时Boost电路要进行充电，所以波动较大。图5中实线为扰动观察法的MPPT仿真，扰动观察法在进行MPPT过程时，其在MPPT处来回振荡，振荡幅度比较大，并且其精度比较低。从仿真图中可以看出曲线比较粗糙，波动比较大。图5虚线为本文方法的仿真曲线，可以看出收敛速度较快，LF?FOA在收敛后功率为353.68 W，与光伏阵列的最大功率相差0.02 W，对比扰动观察法，寻优精度更高，误差更小，在稳定后输出非常平稳，输出功率稳定在最大值。

通过上述分析可知：扰动观察法在进行多峰值最大功率点跟踪时，精度比较低，震荡大，在进行变光照分析时，与其进行对比意义不大，所以进行变光照分析时，只采用LF?FOA算法进行仿真分析。

将光照在0.5 s时，由阴影1变化到阴影2得到图6仿真曲线。

图6  LF?FOA的变光照MPPT仿真

由图6可以明显看到，当光照突变时，引起功率发生变化，本文采用的算法快速重启，在0.5 s时进行重新跟踪，经过轻微震荡后，快速收敛。当光照从阴影1变化为阴影2时，光照强度下降，寻找到最大功率点为234.55 W，与光伏阵列输出功率相差0.03 W，误差小。

通过以上的仿真分析与对比，可以知道LF?FOA算法在进行最大功率跟踪时，收敛速度快，精度高。当光照发生变化时，也能对最大功率点进行快速、可靠的跟踪，对于提升光伏系统的效率具有十分重要的作用，证明了LF?FOA算法的有效性。

4  结  论

本文通过引进莱维飞行优化果蝇算法，并引入最劣解修改果蝇步长，改进了果蝇算法收敛速度慢，容易陷入局部寻优的缺陷，通过函数验证了LF?FOA算法的优越性。在Matlab中进行光伏系统最大功率点跟踪仿真时，仿真结果表明了LF?FOA算法比扰动观察法更优越，同时光照变化时，本文算法也能快速、准确地找到最大功率点。

注：本文通讯作者为李田泽。

参考文献

[1] ZHANG H， JI H， REN J， et al. Research on MPPT control and implementation method for photovoltaic generation syst?em and its simulation [C]// 2009 IEEE 6th International Power Electronics. [S.l.]：  IEEE， 2009： 2108?2112.

[2] 于子捷，魏晨曦，田芳芳，等.一种改进型扰动观察法在最大功率点跟踪中的应用[J].电测与仪表，2017，54（15）：113?119.

YU Zijie， WEI Chenxi， TIAN Fangfang， et al. An improved perturbation and observation method used in maximum power point tracking control of PV generation system [J]. Electrical measurement & instrumentation， 2017， 54（15）： 113?119.

[3] 李星硕，文辉清.基于β参数的变步长MPPT控制研究[J].电力系统保护与控制，2016，44（17）：58?63.

LI Xingshuo， WEN Huiqing. Research on an improved β?based variable step MPPT algorithm [J]. Power system protection and control， 2016， 44（17）： 58?63.

[4] 刘文涛，张容畅，董雨欣，等.一种新型算法在光伏最大功率跟踪中应用[J].电测与仪表，2018，55（1）：72?77.

LIU Wentao， ZHANG Rongchang， DONG Yuxin， et al. Application of a new algorithm in photovoltaic maximum powertracking [J]. Electrical measurement&instrumentation， 2018， 55（1）： 72?77.

[5] ERDEM Z. An advanced particle swarm optimization algorithm for MPPTs inPV systems [J]. Acta physica polonica， 2017， 132（3?II）： 1134?1139.

[6] ISHAQUE K， SALAM Z， AMJAD M， et al. An improved particle swarm optimization （PSO） based MPPT for PV with reduced steady?state oscillation [J]. IEEE transactions on power electronics， 2012， 27（8）： 3627?3638.

[7] 王林，吕盛祥，曾宇容.果蝇优化算法研究综述[J].控制决策，2017，32（7）：1153?1162.

WANG Lin， L? Shengxiang， ZENG Yurong. Literature survey of fruit fly optimization algorithm [J]. Control and decision， 2017， 32（7）： 1153?1162.

[8] PAN Q K， SANG H Y， DUAN J H， et al. An improved fruit fly optimization algorithm for continuous function optimization problems [J]. Knowledge?based systems， 2014， 62（5）： 69?83.

[9] WOLF P， BENDA V. Identification of PV solar cells and modules parameters by combining statistical and analytical methods [J]. Solar energy， 2013， 93（7）： 151?157.

[10] WU L， CAO G. Seasonal SVR with FOA algorithm for single?step and multi?step ahead forecasting in monthly inbound tourist flow [J]. Knowledge?based systems， 2016， 110： 157?166.

[11] YAN B， ZHAO Z， ZHOU Y， et al. A particle swarm optimization algorithm with rand? om learning mechanism and Levy flight for optimization of atomic clusters [J]. Computer physics communications， 2007， 219： 334?343.