面向大图数据的并行图查询

刘小轩

摘  要： 针对传统图模式查询算法难以实现在大图数据上查询或查询时间太长问题，提出基于MapReduce的图查询并行算法PGPQ。该方法包括计算初始匹配节点集、初始不匹配父亲节点集和图模式查询三个部分。在图模式查询过程利用初始不匹配父亲节点集迭代初始匹配节点集中的节点，如果数据图匹配模式图，返回一个最大的匹配。实验结果表明，PGPQ算法查询能有效地进行大图模式查询。

关键词： 并行处理; 图模式查询; 图模式匹配; 大图数据; MapReduce; 实验验证

中图分类号： TN911.1?34; TP311                     文献标识码： A                  文章编号： 1004?373X（2019）20?0045?03

Parallel graph query for large graph data

LIU Xiaoxuan

（School of Control and Computer Engineering， North China Electric Power University， Beijing 102206， China）

Abstract： As the traditional pattern graph query algorithm has the problem that it is difficult to query big graph data or the query time is too long， a parallel graph query algorithm PGPQ based on MapReduce is proposed. The method includes three parts： computation of the initial matched node set， the initial mismatched father node set and graph pattern query. In the graph pattern query process， the initial mismatched parent node set is used to iterate the nodes in the initial matching node set. If the data graph matches the pattern graph， a maximum match is returned. The experimental results show the query of PGPQ algorithm can effectively perform big graph pattern query.

Keywords： parallel processing; graph pattern query; graph pattern matching; large graph data; MapReduce; experimental verification

0  引  言

在过去的几十年中，图查询已经得到了广泛的研究，包括图可达性查询[1]和图模式匹配[2]。一些方法，如基于跳的方法[3?4]和基于覆盖的方法[5?6]经常被采用。它们之间的区别是如何构建互补的索引，该编码将编码的剩余可达性信息编码在基盖之外。基于跳的方法通常具有比基于覆盖的方法小得多的索引大小，并且将基于跳的可达性索引集成到其他索引框架（如圖模式匹配）[7]中更简单。

图模式匹配在不同领域中被证明是有用的[8]，目前已经通过子图同构提出了几种算法。还有一些基于图模拟的一些方法[9?12]。文献[10]研究了基于图模拟的模式图，它考虑了路径的有界长度和节点属性约束和搜索条件的节点。文献[11]提出了一种弱相似性的概念，该方法通过将边映射到无界的路径，从而扩展了图模拟，它关注子图相似度，是一个NP?hard问题。文献[12]在模式图中考虑有界连通性，其中模式在所有边上施加相同的边界，并且基于子图同构的扩展来进行图匹配，这仍然是NP?hard问题。

近年来，已经有些基于大图数据的图查询的研究[13?14]。文献[13]解决了大型网络中的图查询优化问题，文献[14]中对查询的尺度无关性的概念进行了形式化。为了使查询响应在大数据集中可行，文献[15?16]中提出了一些并行图匹配方法。文献[15]提出了一种图模拟的分布式算法，通过首先计算部分匹配，增强了数据模拟的数据局部性，从而优化了数据传输和查询时间。然而，强连通分量在图匹配期间会导致较差的数据局部性，因为只有在强连通分量中的G的所有节点都在一个机器内时，才可以执行图G上的匹配。文献[16]提出了一种强模拟的分布式算法[17]，首先使网络流量可控，保证了强模拟的更低时间复杂度。文献[10]中的工作，通过放宽子图同构条件提出一种立方时间内图模式匹配方法。文献[17]提出基于六度分隔理论的可达索引，为图中每一个点建立一个六度可达索引，解决局部查询问题。因为实际应用中绝大多数应用查询都应该在六度以内。本文通过使用文献[17]中六度可达索引，基于MapReduce对文献[10]中的图匹配算法并行化，以实现在大图数据上高效的图模式查询。

1  图模式匹配

首先简要地给出了文献[10]中关于图模式查询的初步研究，并且使用mat（）记录初始匹配节点集，使用premv（）记录初始不匹配父亲节点集，使用desc（）记录后代节点，使用anc（）记录祖先节点集。

定义1 数据图。G（V，E，fA）是一个有向图。V表示数据图G上所有的节点集合;E表示数据图G上所有的有向边集合，[E?V×V];fA是定义在V上的一个函数，对于每一个节点v，[v∈V]，fA（v）表示节点v的属性元组，fA（v）={A1=a1，a2，…，An=an}，对于每一个元组“Ai=ai”，表示节点v有一个属性为Ai，属性值为ai。在G中一条路径是一系列v1/…/vn的节点，其中（vi，vi+1）是在G中的一条边，[i∈[1，n-1]]，把v2称为v1的孩子（或v1是v2的父亲），vi是v1的后代节点，i∈[2，n]。

定义2 模式图。P（Vp，Ep，fe，fv）为模式图。Vp表示P上的节点集;Ep表示有向边集;fe是一个定义在Ep（u，u）上的函数，表示有向边（u′，u）在G中对应的有向路径（v′，v）的长度的约束限制;fv是一个定义在Vp上的一个函数，对于P中的每一个节点u，fv（u）表示结果图G′中与u匹配的节点的属性应该满足的条件。对于每个属性条件限制使用的“A op a”的形式，其中A代表某个属性;op代表操作符{<，>，=，<=，>=，！=，has}，a代表属性值。

定义3 有界的图模拟。给定数据图G=（V，E，fA）和模式图P=（Vp，Ep，fe，fv），如果存在一个二元关系[R?V×Vp]，通过有界的模拟，满足以下条件，则G匹配P。

1） 对Vp中每个节点u，在V中存在v使得（u，v）∈R。

2） 对每一个（u，v）∈R，v的属性fA（v）满足u的谓词fv（u），也就是说，在fv（u）对于每个原子公式“A op a”，在fA（v）上定义v，A=a′，而且“a′ op a”;对于Ep中的每条边（u， u′），G中存在非空路径p=v/…/v′，如果fe（u，u′）是常数k，使得（u，u′）∈R和len（p）≤k。

定义4  mat（u）。让G=（V，E，fA）是一个数据图并且P=（Vp，Ep，fe，fv）是一个模式图。对Vp中任意节点u， mat（u）={x|x∈V，fA（x）满足fv（u）， 并且 out?degree（x）≠0 if out?degree （u）≠0}。

定义5  premv（u）。让G=（V，E，fA）是一个数据图并且P=（Vp，Ep，fe，fv）是一个模式图。对Vp中任意节点， premv（u）={x|x∈V，out?degree（x）≠0， 并且存在（u′，u）∈Ep（x′∈mat（u），fA（x）满足fv（u′），并且len（x/…/x′）≤fe（u′， u））}。

定义6  anc（x）。让G=（V，E，fA）是一个数据图并且P=（Vp，Ep，fe，fv）是一个模式图。对集合V任意节点x， anc（x）={x′|x′∈V，（u′，u）∈Ep（fA（x）满足fv（u），fA（x′）满足fv（u′）并且len（x′…x） ≤fe（u′， u））}。

定义7  desc（x）。让G=（V，E，fA）是一个数据图并且P=（Vp，Ep，fe，fv）是一个模式图。对集合V任意节点x， desc（x） ={x′|x′∈V，（u′，u）∈Ep（fA（x）满足fv（u），fA（x′）满足fv（u′）并且len（x′…x） ≤fe（u′，u））}。

2  并行图模式查询算法流程（PGPQ）

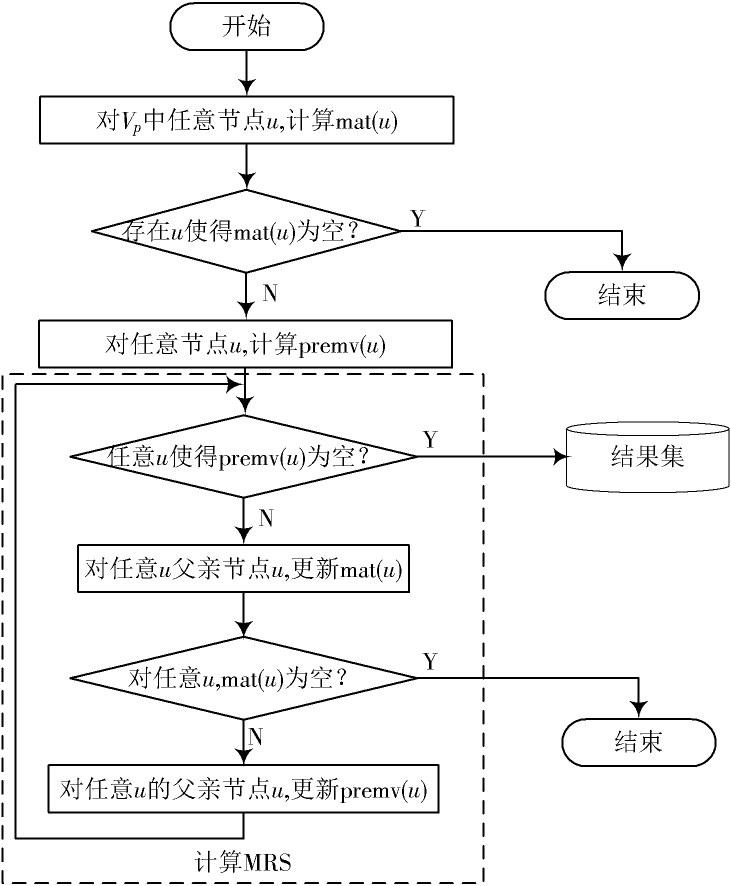
在PGPQ算法中使用MRS（Matched Result Set）记录匹配结果集。PGPQ算法包括两个阶段：第一个匹配预处理阶段计算mat（）和计算premv（）;第二个图查询阶段计算MRS（）。PGPQ算法流程如图1所示。首先，计算初始匹配节点集;然后，计算初始不匹配父節点的节点集;最后，使用premv（）不断地清洗mat（）中不满足条件的节点，返回匹配结果集为空集或为最大的匹配。

图1  算法流程

3  实验分析

3.1  实验数据及环境

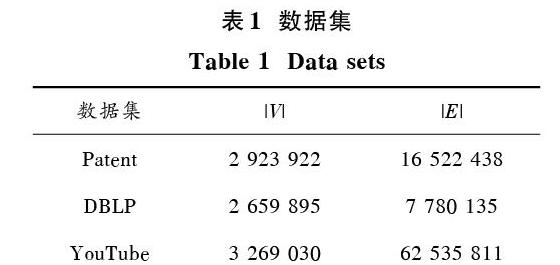
本文使用以下几个实际应用中的数据集，其中数据集分别是：Patent数据集[18] 、DBLP数据集和YouTube数据集。

表1  数据集

Hadoop集群基于Ubuntu系统，使用VMware Workstation搭建，由8个虚拟机组成分布式并行计算环境，其中8台物理机通过100 Mb/s路由器连接。

3.2  实验结果

实验部分对PGPQ算法加速比进行了评估，还对比了两种不同的距离探测方法（基于六度可达索引的查询和基于BFS算法在线距离探测的查询）。此外，六度可达索引离线建立，不计入查询时间。对于模式图使用P（x，y，z）表示，x表示模式的节点数Vp，y表示模式的边数Ep，z表示k跳数。

3.2.1  PGPQ算法加速比分析

对于加速比评估，分别采用1，2，4和8个节点对不同数据集中的使用模式图P（6，6，3）查询，并记录有效的运行时间。PGPQ加速比如图2所示。

图2  PGPQ算法加速比

[11] NARDO L D， RANZATO F， TAPPARO F. The subgraph similarity problem [J]. IEEE transactions on knowledge & data engineering， 2008（5）： 748?749.

[12] ZOU L， CHEN L， ZSU M T. Distance?join： pattern match query in a large graph database [J]. VLDB endowment，2009， 2（1）： 886?897.

[13] ZHAO P X， HAN J W. On graph query optimization in large networks [J]. Proceedings of the VLDB endowment， 2010， 3（1/2）： 340?351.

[14] FAN W， GEERTS F， LIBKIN L. On scale independence for querying big data [C]// ACM Symposium on Principles of Database Systems. Snowbird  Utah： ACM， 2014： 51?62.

[15] MA S， CAO Y， HUAI J P， et al. Distributed graph pattern matching [C]// Proceedings of 21st Annual Conference on World Wide Web. Lyon： [s.n.]， 2012： 949?958.

[16] WANG H Z， LI N， LI J Z， et al. Parallel algorithms for flexible pattern matching on big graphs [J]. Information sciences， 2018， 436/437： 418?440.

[17] 高延太.基于并行处理大数据图查询研究[D].北京：华北电力大学，2017.

GAO Yantai. Research on graph query of large data based on parallel processing [D]. Beijing： North China Electric Power University， 2017.

[18] National Research Council of the National Academies. Frontiers in massive data analysis [M]. Washington： The National Academies Press， 2013.