例谈初中数学含参数运算的几种策略

陈艳胜

[摘 要]参数经常出现，它兼有常数和变数的双重特征。参数运算将思维和运算有机地结合在一起，考查考生的思维能力、运算能力。在解决含参数的问题时常求出参数取值范围。

[关键词]参数;待定系数法;函数最值

参数是用字母加以表述的，它兼有常数和变数的双重特征。参数问题能有效地考查考生的思维能力、运算能力、推理能力，是近年来中考命题的常见题型。下面笔者结合自身的教学实践谈谈含有参数问题的几点处理策略。

一、渗透换元思想，巧用字母代替数，在数学计算中化难为易

有些繁难的数学计算，可以引入参数，利用等式的变形的有关技巧消元，化难为易。

例：若x=123456789×123456786，y=123456788×123456787，试比较x、y的大小.

解：设123456788=a，那么 x=（a+1）（a-2）=a2-a-2， y=a（a-1）=a2-a o

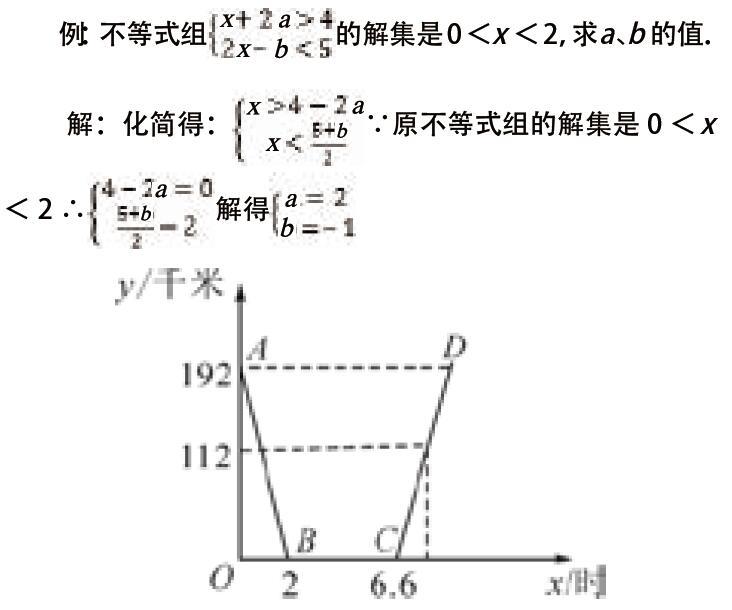
∵x-y=（a2-a-2）-（a2-a）=-2<0o∴x

二、明确哪个量为参量，并对参量进行讨论或求参量的取值范围

（一）参数取值的不确定性，引发对参数的讨论

在初中阶段提及的整式方程或分式方程中出现的未知数常以字母x、y、zo表示，而其他字母（如a、b、m、no）都看成常数（参数）。

例：当m为何值时，关于x的方程（m?-4）x?+2（m+1）=0有實根？

分析：把xo看成未知数，mo看成参数，把方程的两个解用含参数om的代数式表示，再求解。

解：m?-4=0时，即m=2或-2时，方程化为：0+2（m+1）=0，无解;

m不为2或-2时，有x?=-2（m+1）/（m?-4）得：m<-2， 或-1<m<2综合得：m<-2，或-1

（二）多元方程组中，先确定主元，再确定参数，把主元用参数的形式表示

例：已知，xyz≠0，求的值。

分析：确定主元x、y，再确定参数z，用含z的式子表示x、y，再代入算式约去参数。

解：整理得解得代入代数式计算再约去z。

（三）不等式（组）参数的取值范围如何确定

1.不等式的性质解题。含参数的不等式常要讨论求解。

2.根据不等式组的求解方法求解。若其中一个不等式含有参数，则可根据未知数的解集，求参数的取值范围。

例：不等式组的解集是0

解：化简得：∵原不等式组的解集是0

三、用待定系数法求参数的值

在初中数学一次 、二次 、反比例函数的解析式求法最主要用待定系数法确定参数的值。

例： 昨天早晨7点，小明乘车从家出发，去参加中科技创新大赛，赛后，他当天按原路返回，如图，是小明昨天出行的过程中，他距西安的距离y（km）与他离家的时间x（时）之间的函数图象. 根据下面图象，回答下列问题：（1）求线段AB所表示的函数关系式; （2）已知昨天下午3点时，小明距西安112km，求他何时到家？

分析：用待定系数法解得k=-96，b=192，故线段AB所表示的

函数关系式为：y=-96x+192（0≤x≤2）

四、参数的取值范围对函数最值的影响

当函数解析式确定时，自变量的取值范围会影响到函数图象。同样的函数解析式，值域就受定义域的影响。尤其是二次函数的区间最值问题、一元二次方程根的分布问题。

例：已知二次函数y=ax2+2ax+3a2+3（其中x是自变量），当x≥2时，y随x的增大而增大，且﹣2≤x≤1时，y的最大值为9，则a的值为______.

【解析】∵二次函数y=ax2+2ax+3a2+3（其中x是自变量），∴对称轴是直线x=﹣2a/2a=﹣1，

∵当x≥2时，y随x的增大而增大，∴a>0，∵﹣2≤x≤1时，y的最大值为9，

∴x=1时，y=a+2a+3a2+3=9，∴3a2+3a﹣6=0，∴a=1，或a=﹣2（舍去）.