全氟辛烷磺酸在大连区域环境多介质中的归趋模拟

谷晓悦，丁光辉，刘全斌，李婉然，薛欢欢

大连海事大学环境科学与工程学院，大连 116026

全氟烷基化合物(PFASs)是一类人造化学品，生产于20世纪50年代，并且于20世纪70年代后在全球范围内广泛使用[1]。由于其疏水性和疏油性，被广泛应用于世界各个行业和消费者产品中，如地毯表面保护剂、表面活性剂、润滑剂、农药、纺织涂料、不粘涂料、防污剂、食品包装、水性成膜泡沫和化妆品[2-3]。近年来的研究发现，PFASs具有长距离迁移性、环境持久性和生物累积性，对生物群和人类造成不利影响[4-5]。因此，PFASs成为一类备受关注的化学品[6-8]。其中，全氟辛烷磺酸(PFOS)是最主要生产和应用的PFASs，在各种环境介质中普遍检出，且含量较高，因此成为主要研究的PFAS。2009年5月，PFOS及其盐类被列入“斯德哥尔摩公约”附件B，成为被“限用”的持久性有机污染物(POPs)。虽然大多数发达国家已逐步淘汰PFOS的生产和使用，但中国却成为PFOS相关化学品的主要生产国，2001—2011年间进出口销售的总量约为1 800 t[9]。因此，近年来在中国的多种环境介质和生物体中频繁检出PFOS[10]，且东部沿海发达地区的PFOS污染水平高于西部地区。由于持久性，进入环境的PFOS在环境各介质中存在时间较长，且在相间迁移。因此，有必要研究其在环境多介质间的迁移规律和环境归趋，以期为PFOS的污染控制和生态风险评价提供科学依据。

多介质逸度模型已成为研究环境中污染物迁移和归趋行为的最有效工具之一[11-12]。汪祖丞等[13]利用三级逸度模型分析了稳态假设下菲在长江口地区不同环境介质间的分布规律；刘炳光和佟玉洁[14]应用多介质逸度模型研究点源排放的五氯酚在天津水环境中的迁移转化规律；印红玲等[15]运用多介质模型对成都地区典型的7种有机磷酸酯阻燃剂的环境分布进行了模拟；任娇等[16]运用三级逸度模型模拟了青藏高原纳木错流域4种POPs的迁移和归趋行为。大连市以港而建，作为我国中国东北地区重要的经济、贸易、港口、工业和旅游城市，在经济发展的同时，也引起了不同程度的环境污染问题[17]。虽然已有文献报道大连市不同环境介质中PFASs的污染水平及分布，但是关于其在不同环境介质间的迁移和归趋研究较少。因此，本文以大连为研究区域，通过建立三级逸度模型来研究PFOS在大气、土壤、水及沉积物4个不同环境相间的迁移和归趋行为，以期为其污染控制和生态风险评价提供科学依据。

1 材料与方法(Materials and methods)

1.1 研究区域

大连市位于辽东半岛南端，黄渤海之滨，地处E120°58'～E123°31'；N38°43'～N40°10'具有海洋性特点的暖温带大陆性季风气候，夏季降水量丰富，年降水量550～950 mm，平均风速为5.3 m·s-1。大连地区主要有黄海流域和渤海流域两大水系。研究区域见图1。其中，土壤面积为1.34×1010m2，大气面积为1.37×1010m2。研究中选取平均水深为1 m，平均土壤厚度为0.1 m的经验值作为三级逸度模型的输入参数[18]。

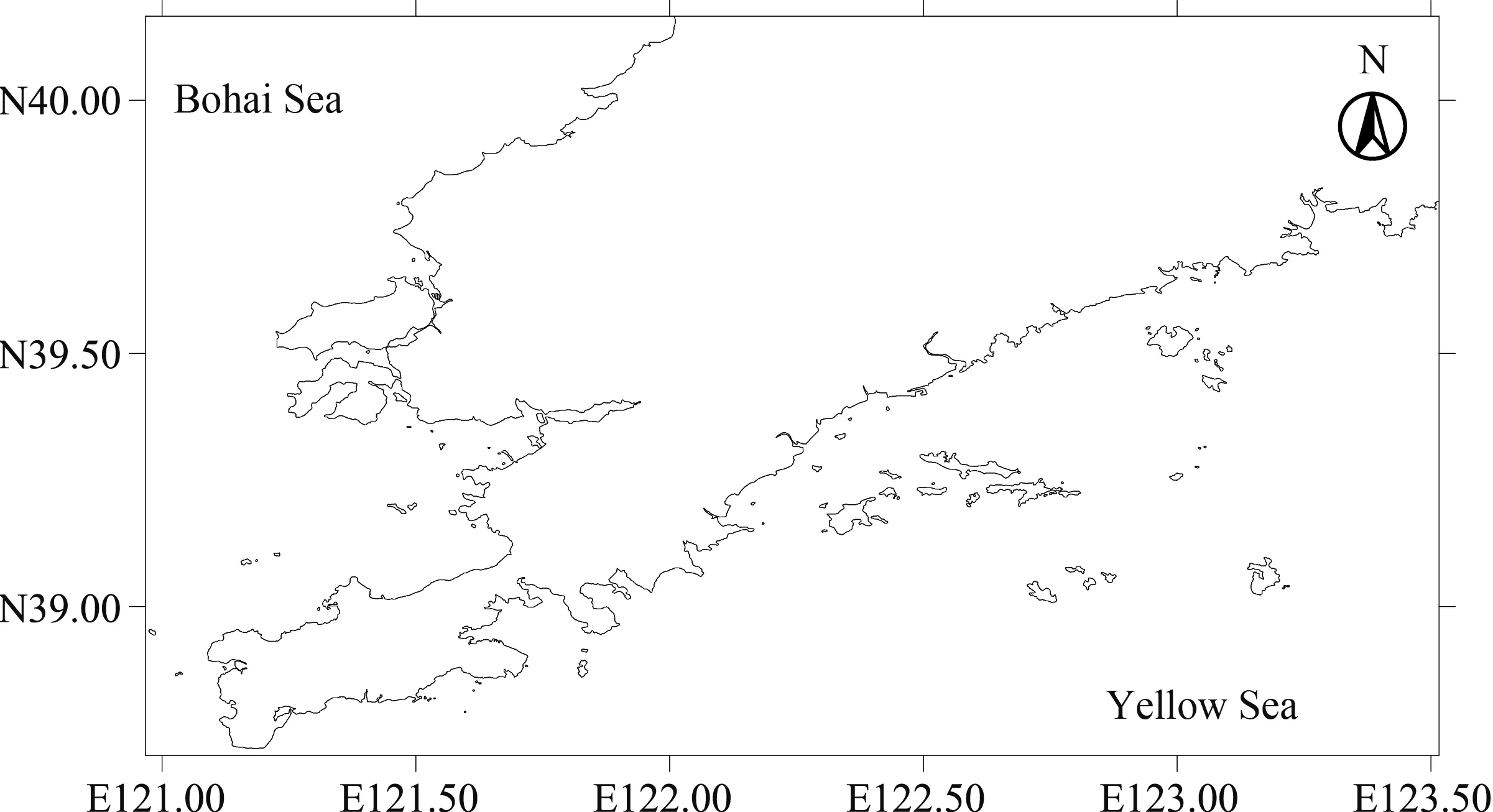
图1 大连地区研究区域图Fig. 1 The study area of Dalian

1.2 研究方法

1.2.1 模型框架

本文采用Mackay的环境多介质三级稳态模型，假设研究区域为稳态非平衡流动系统，结合该区域的地理、气候和环境因素，研究了PFOS在水体、大气、土壤和沉积物等环境相间的迁移和归趋行为。PFOS在研究区域的输入过程包括污染物的直接排放和平流输入；在各介质间的迁移包括大气的干湿沉降、地表径流、颗粒物的降解再悬浮和水体与沉积物间的扩散等；输出过程包括PFOS在环境中的降解及平流输出。基于三级稳态多介质逸度模型，结合大连市实际情况，根据稳态假设和质量守恒定律建立平衡方程[18]，如式(1)～(4)所示：

空气相：EA+GACA+fWDW-A+fSDS-A=fA(DA-W+DA-S+DR(A)+DA(A))

(1)

水相：EW+GWCW+fADA-W+fSDS-W+fSedDSed-W=fW(DW-A+DW-Sed+DR(W)+DA(W))

(2)

土壤相：ES+fADA-S=fS(DS-A+DS-W+DR(S)+DA(S))

(3)

沉积物相：ESed+fWDW-Sed=fSed(DSed-W+DR(Sed)+DA(Sed))

(4)

式中：A、W、S、Sed分别代表大气、水、土壤和沉积物，Ei代表污染源向环境相i中排放污染物的排放速率(mol·h-1)；Gi代表向环境相i输入污染物的平流速率(m3·h-1)；Ci代表平流流入环境相i中污染物的浓度(mol·m-3)；fi为环境相i的逸度(Pa)；Di-j为环境相i到环境相j的迁移参数(mol·h-1·Pa-1)；DR(i)为污染物在环境相i的降解速率(mol·h-1·Pa-1)；DA(i)为污染物在从环境相i的平流输出速率(mol·h-1·Pa-1)。

1.2.2 模型输入参数

模型输入参数包括为污染物的理化性质参数、环境参数、污染物在环境介质间的迁移参数及污染物的排放速率和平流输入浓度等参数。通过查阅大量文献资料并结合大连市地区的实际情况，对模型输入参数进行反复校正与确认后选取最有代表性的参数数据，详见表1～3。其中，对于排放源本文仅考虑大气和水体排放，故大气排放速率用总排放速率和水体排放速率的差值计算得出。

1.2.3 参数灵敏度分析

灵敏度(CS)是用来评估输入参数对输出结果的影响程度的参数。对输入参数(除常数)进行灵敏度分析，灵敏度越大的输入参数对模型结果的影响越大，灵敏度由公式(5)计算[16]：

CS=(Y1.1-Y0.9)/(0.2×Y1.0)

(5)

式中：Y1.1、Y0.9和Y1.0分别表示取1.1、0.9和1.0倍的输入参数时输出的模型结果。CS>0时，表示输入参数对输出结果有正影响；反之，CS<0时，表示输入参数对输出结果有一定的负影响。由于考察参数较多，本文以∣CS∣>0.2为标准，筛选出灵敏度较大的参数。

1.2.4 不确定度分析

蒙特卡洛法，是基于“随机数”的计算方法[28]。以概率论中的大数定理和中心极限定理为理论基础，其基本原理可由式(6)表示。

表1 全氟辛烷磺酸(PFOS)的理化性质参数[19]Table 1 Physicochemical properties of perfluorooctane sulfonate (PFOS) [19]

表2 PFOS的环境迁移参数Table 2 Environment migration parameters of PFOS

表3 大连地区PFOS的排放速率和平流输入浓度Table 3 The emission rate and advection input concentration of PFOS in Dalian area

假定函数

Y=f(X1, X2, ..., Xn)

(6)

式中：Y表示某一环境相中PFOS的浓度，Xn表示灵敏度大于0.2的输入参数。通过随机抽样取出每一组随机变量X1, X2, ..., Xn的值x1, x2, ..., xn，通过关系式(7)确定函数Y的值yi；

yi=f(x1i, x2i, ..., xni)

(7)

经过反复多次独立抽样(i=1, 2, ..., 10 000)，得到函数Y的一批抽样数y1, y2, ..., yn，数值符合正态分布特征。模拟次数越多，则可得出与实际结果越相近的概率分布。

本研究应用蒙特卡洛方法对输出的PFOS浓度进行不确定度分析，对∣CS∣>0.2的输入参数在合理范围内取值，在MATLAB平台上进行编程运行10 000次，计算四分位差，分析其不确定性。

2 结果与讨论(Results and discussion)

2.1 模型验证

根据三级逸度模型，PFOS在大气、水、土壤和沉积物相中的预测浓度分别为5.10 pg·m-3、22.60 ng·L-1、2.25 μg·kg-1和0.34 μg·kg-1。对于PFOS在土壤和沉积物中的浓度，可通过土壤/沉积物密度及PFOS的摩尔质量将单位从“μg·kg-1”转换成“mol·m-3”。其中，沉积物和土壤的密度分别取1 500和2 600 kg·m-3 [18]。为验证其准确性，与文献[23,29-31]中报道的实测值进行比较(见图2)。由图2可以看出PFOS在大气、水和土壤中的模拟值分别低于实测值0.16、0.20和0.78个对数单位，在沉积物中的模拟值则高于实测值0.50个对数单位，偏差均在1个数量级范围内。一般情况下，考虑到实际情况的复杂性、非稳态及平衡性，模型预测结果与实测值的偏差在1个数量级以内均为合理[32]。大气中PFOS的模拟值低于实测值0.16个对数单位，可能是因为模型采用总排放量减去水体排放量对大气排放量进行估算，忽略了人口密度和工业发展对排放量的影响，使得预测的大气排放量偏低，最终导致大气的预测值偏低。PFOS在水中的预测值低于实测值0.20个对数单位，可能是由于模型以污水处理厂的排放量作为水体排放量估算的依据，未考虑周围生活污水和工业污水直接排放的影响。另外，大连湾海域属于半封闭海域，水体交换能力有限，周围生活污水和工业污水的排放的PFOS不易扩散到外海，也可导致预测值偏低。PFOS在土壤中的预测值低于实测值0.78个对数单位，原因为：(1)本研究未考虑PFOS向土壤的排放量，导致预测值偏低；(2)土壤中PFOS的降解速率来自于文献[19]，受各种地理环境因素的影响，PFOS在大连地区的土壤降解速率可能低于文献参考值，从而导致模型

图2 PFOS在大连地区大气、水、土壤和沉积物相中模拟浓度和实测浓度Fig. 2 Simulated and measured concentrations of PFOS in atmosphere, water, soil and sediment phase of Dalian

预测值偏低。PFOS在沉积物中的预测值则高于实测值0.50个对数单位，可能是由于三级模型为稳态、非平衡和流动的系统[33]，而实际情况为非稳态、非平衡和流动的系统，这样的差异导致预测值偏高。另外，由于目前PFOS的相关分配系数和扩散系数都是基于纯水测定的，缺少基于海水的测定值，因此本研究未能考察海水盐度的影响，可能导致预测结果存在一定的偏差。为进一步分析模型精确度，计算了PFOS在不同环境介质中的实测值和预测值间的相对偏差。结果表明：大气、水、土壤和沉积物相的实测值和预测值间的相对偏差分别为0.01、0.03、0.15和-0.09，气相浓度预测值与实测值偏离程度最小，土壤相浓度预测值与实测值偏离程度最大，但总体实测值和预测值间的相对偏差程度较小。综上所述，模型较适用于预测PFOS在大连区域多环境介质中的浓度。

2.2 PFOS在大连地区环境多介质间的迁移和归趋行为

通过逸度进一步计算PFOS在环境多介质间的迁移和归趋行为，如图3所示。由计算结果可知，PFOS在大连地区环境相间的迁移主要是由大气相向土壤相中迁移(2.46×103mol·a-1)和土壤相向水相迁移(2.45×103mol·a-1)，分别占相间总迁移量的45.27%和45.09%。可见水和土壤是大连地区PFOS的主要的汇，其原因与PFOS的大气干湿沉降有关。大连市属于沿海城市，风速较大，降雨较多。大气沉降速率与风速呈正相关[34]，导致大连地区大

图3 PFOS在大连地区环境多介质间的迁移和归趋行为注：A、W、S、Sed分别代表大气、水、土壤和沉积物，Ei代表污染源向环境相i中排放污染物的排放速率(mol·h-1)；Gi代表向环境相i输入污染物的平流速率(m3·h-1)；Ci代表平流流入环境相i中污染物的浓度(mol·m-3)；Di-j为环境相i到环境相j的迁移参数(mol·h-1·Pa-1)；DR(i)为污染物在环境相i的降解速率(mol·h-1·Pa-1)；DA(i)为污染物在从环境相i的平流输出速率(mol·h-1·Pa-1)。Fig. 3 Transfer and fate of PFOS in environmental multimedia of Dalian areaNote: A, W, S and Sed represent the atmosphere, water, soil, and sediment, respectively. Ei represents the emission rate of pollutants discharged into the environmental phase i (mol·h-1); Gi represents the advection rate of pollutants input to the environmental phase i (m3·h-1); Ci represents the concentration of pollutants flowing into the environmental phase i (mol·m-3); Di-j is the transfer parameter from the environmental phase i to the environmental phase j (mol·h-1·Pa-1); DR(i) is the degradation rate of pollutants in the environmental phase i (mol·h-1·Pa-1); DA(i) is the advection output rate of pollutants from the environmental phase i (mol·h-1·Pa-1).

气干湿沉降率较大，由此，PFOS的大气向土壤的迁移成为主要的相间迁移，地表径流作用也使土壤相向水相的迁移成为主要的相间迁移过程。对于区域迁移而言，PFOS在大气和水相的平流输入是PFOS的主要来源。PFOS在大气和水相的平流输出也相当大，其中水体平流输出远大于大气平流输出，导致周边海域受到近岸PFOS排放的污染，同时大气的平流输出也会导致大连下风向地区受到PFOS污染。

2.3 灵敏度分析

参数灵敏度的大小反映出参数对模型结果的影响程度，对其进行分析有助于优化模型结果，阐明主要影响因素。本文以∣CS∣>0.2为标准，筛选出灵敏度较大的参数，分析结果表明，有机碳分配系数、溶解度、水和气相平流输入、土壤中水的径流速率以及温度输入参数对模型输出结果影响较大(见表4)。对于气相而言，PFOS的大气平流输入对气相浓度影响较大，CS达到1，表明大连区域上风向污染物排放对环境影响较大。对于水相而言，PFOS的水体平流输入对水相的浓度影响较大，CS达到1，表明水体的上游区域污染物排放是影响该区域PFOS含量的重要因素。对土壤相而言，有机碳分配系数、蒸气压、溶解度、大气的平流输入、土壤中水的径流速率以及温度对污染物在土壤相的浓度有较大影响，∣CS∣都可达到1左右，有机碳分配系数、大气平流输入和温度都显示出对土壤相浓度有正影响，其原因是，污染物的有机碳分配系数越高，越容易吸附在土壤中的有机碳相，导致土壤相中污染物浓度升高，而大气平流输入和温度越高，会增强大气-土壤间的扩散，也导致土壤相中污染物浓度升高[35]；其中溶解度和土壤中水的径流速率对土壤相浓度有负影响，其原因是溶解度越大溶淋效果越强，导致污染物从土壤相向水相迁移，而土壤中水的径流速率越大污染物也会随径流作用加速从土壤相迁移至水体中，使得土壤相中污染物浓度减少。对于沉积物相而言，有机碳分配系数和PFOS的水体平流输入对沉积物浓度有较大的影响，灵敏度都达到1以上，其原因同土壤相同，污染物的有机碳分配系数与其对有机碳的吸附能力呈正比，使得污染物吸附在沉积物中，沉积物中浓度增高，而水相平流输入越大，水-沉积物相间的扩散越明显，也导致沉积物中浓度升高。由此表明，上述参数是影响PFOS在相间迁移的重要因素，精确确定这些灵敏度较大参数的数值有益于提高预测结果的准确性。

表4 不同输入参数灵敏度分析Table 4 The sensitivity analysis of different input parameters

注：“”表示∣Cs∣<0.02；Cs表示灵敏度。

Note: “” means ∣Cs∣<0.02; Csstands for sensitivity.

2.4 不确定性分析

应用蒙特卡罗方法对输出浓度进行不确定度分析，根据区域环境实际情况对∣CS∣>0.2的输入参数在合理范围内随机取值10 000次，在MATLAB中进行编程，进行蒙特卡洛模拟。模拟输出结果显示，大气、水体、土壤及沉积物相的输出浓度分别为4.72 ～6.71 pg·m-3、4.33～24.60 ng·L-1、1.48～4.17 μg·kg-1及0.29～0.36 μg·kg-1。计算出大气、水体、土壤和沉积物的模拟浓度四分位差，分别为0.50 pg·m-3、3.37 ng·L-1、0.34 μg·kg-1和0.02 μg·kg-1。其中，水体中PFOS的四分位差相对较大，说明输入参数的整体变化对水体输出浓度有一定影响，因此，在建模中应注意规范水体输入参数以提高输出结果的准确度。

综上所述：本文建立了三级逸度模型对PFOS在大连区域大气相、水相、土壤及沉积物相的浓度进行模拟，其模拟值分别为5.10 pg·m-3、22.60 ng·L-1、2.25 μg·kg-1和0.34 μg·kg-1。与实测值相差均在1个数量级以内，说明模型拟合度较高，预测结果较为可信。大气向土壤迁移以及土壤向水的迁移是环境相间迁移的主要途径，分别占总环境相迁移量的45.27%和45.09%。而大气和水的平流输入和输出是环境污染的主要来源和损失途径。根据灵敏度分析的结果，有机碳分配系数、溶解度、大气和水的平流输入、土壤中水的径流速率以及温度的灵敏度较大，对模型结果有一定的影响。不确定性分析结果显示，整体参数的改变对水体输出结果影响最大，对沉积物的结果影响最小。本研究较好地模拟了PFOS在大连区域环境多介质中的迁移和归趋，可为其污染控制和生态风险评价提供科学依据。

致谢：感谢国家自然科学基金(51479016)及辽宁省自然科学基金(20180510004)对本研究的资助。