基于Penman-Monteith模型分时段模拟华北落叶松日蒸腾过程

陈 琪，李远航，王琼琳，王 莉，林 莎，贺康宁

(北京林业大学水土保持学院，水土保持国家林业局重点实验室；北京市水土保持工程技术研究中心； 林业生态工程教育部工程研究中心，100083，北京)

蒸腾在土壤-植物-大气连续体(soil-plant-atmosphere continuum)水汽的传输过程中发挥着重要的作用[1]。树干边材的上升液流提供了林木个体蒸腾耗水的99.8%以上[2]，只有极少的水分被根系吸收以后留在了林木体内；因此它是衡量植物蒸腾耗水的一个重要的指标，可以反映出环境因素对于植物体内水分平衡的调节作用。以往的研究发现热扩散式探针法、组织平衡法和热脉冲法[3]可以实现树干液流的持续观测，树木的液流速率和蒸腾速率有着很好的相关性，可以估算整株林木或者整片林分的实际蒸腾量[4]。

计算林木蒸腾量的理论多涉及Penman-Monteith方程，该方程可以计算水分亏缺状态下的林木蒸腾量，而且可以包括小时、天以及月在内的多个时间尺度，是当前公认的估算精度高、适用性广、可靠的蒸散计算通用方程[5]。该方程涉及参数众多，参数的变化直接影响着方程的应用，绝大部分参数可以通过完整的理论和精密的实验仪器获得，但是冠层整体气孔阻力γst(s/cm)却无法得到准确结果。通过LI-1600实测能够获得低矮农作物的冠层叶片气孔阻力[6]，但冠层结构复杂的乔木很难得到不同冠层的气孔阻力[7]。该方程在计算林木蒸腾时受到限制，因此γst的深入研究是当前植被蒸腾研究的一个热点问题。笔者旨在利用茎流计数据反推γst[8]，此时反推求出的γst不仅包括Penman-Monteith方程中其他参数在测量或者计算过程中所产生的误差，同时也是对于另外的那些参数的误差的一个修正，利用γst与同步的气象因子之间建立回归方程，利用常规气象因子得出精度较高的γst，进而结合Penman-Monteith方程模拟林木的蒸腾，蒸腾是植被主要的耗水形式，研究黄土干旱地区林木的实际蒸腾量，对于提高林木水分的利用效率，加强林地植被的建设和管理以及维持林分的稳定有着重要的研究意义，同时分析其蒸散耗水特性也对调控水分关系，解决干旱地区水分供需矛盾具有重要的指导意义。

1 研究区概况

大通县是属于青海省西宁市的下辖县，地处青海省东部，祁连山南麓，三面环山，是青藏高原和黄土高原的过渡地带。海拔2 280～4 622 m，地势西北高东南低，深居内陆，属高原大陆性气候，比较寒冷、干燥，年降水量523.3 mm，年平均蒸发量1 762.8 mm，年平均相对湿度56%，年平均日照时间2 553 h。试验区位于大通县的安门滩小流域，试验区的土壤类型为黄土母质上发育的山地棕褐土和栗钙土，土层深厚。

2 材料与方法

2.1 研究方法

1)茎流计测定。本文采用Sapflow-32植物茎流观测系统(美国Dynamax公司生产)对大通县安门滩华北落叶松(Larixprincipis-rupprechtii)的实际蒸腾量进行全天候观测。茎流观测系统可以安装基于热扩散原理(TDP，thermal dissipation sap velocity)的探针式热扩散传感器，因此被称作热扩散式探针法[9]。

在安门滩的固定样地内选取生长状况良好的华北落叶松，为了减少太阳光直射引起温度变化的误差，在树木北侧胸径出插入探针，用砂纸打磨树干(5 cm×5 cm)，然后在树干磨平处平行于树干方向上间隔3 cm打孔，钻孔的深度约为边材的半径，最后将TDP热扩散探针平行插入钻孔位。采用橡皮泥固定TDP热扩散探针与树木的接触位置，并包裹防水胶带。茎流数据采集的时间间隔为10 min。

液流速率计算公式采用由Granier(1987)确定的[10]：

(1)

式中：f为平均液流速率，cm/min；Δtmax为1 d之内的2个探针之间最大的温度差，℃；Δt为2个探针的瞬时温度差，℃。

2)气象要素测定。在安门滩固定样地的附近空地上布设Davids便携式自动气象站，与茎流计测定同步观测降雨量、太阳辐射、温度、相对湿度、风速、气压等主要的气象因子，数据采集时间间隔10 min。笔者为了研究温度和湿度的协同效应还考虑了饱和水汽压差VPD这项气象指标。其计算方法[11]为

(2)

式中：VPD为饱和水汽压差，kPa；t为温度，℃；RH为空气相对湿度，%。

3) 叶面积指数。华北落叶松的生长季的叶面积指数(leaf average index，LAI)采用冠层分析仪拍摄照片所得，拍摄时间选择阴天、早上或者傍晚[12]，采用WinSCANOPY 2006a分析软件对图片进行处理计算。拍照时间间隔1周，雨后加测。

4) 数据处理。运用Origin 2018 和 Microsoft Excel 2010记录、整理实验数据，并绘图，运用 SPSS 18. 0 统计分析软件Pearson法对试验数据进行回归分析。

2.2 应用理论

1 )Penman-Monteith方程(P-M方程)。彭曼联合法(Monteith，1965)是预测树木蒸腾量的模型中的首选，Monteith(1965)在Penman(1948)方程的基础之上，引入气孔阻力(γc)的概念从而改进得到了彭曼联合法方程[13]，该方程是以水汽扩散理论和能量平衡为理论基础，即考虑了空气动力学因素又考虑了植物的生理因素对于树木蒸腾的影响[14]，具有很广的适用性和较高的计算精度。

P-M方程的基本形式为

(3)

在假定动量热量和水汽输送的边界层阻力相差较小(忽略温度层结问题)，即令γah(热传输阻力)≈γav(水汽传输阻力)≈γa，并考虑气压订正后，用γst(冠层整体气孔阻力，s/cm)代替气孔阻力rc[15]，得到下式：

(4)

乔木的γst一般采用间接方法推导，具体的推算方法是利用安装在落叶松树干上面的茎流计的数据求算得到整株蒸腾量，然后利用P-M方程反推求出γst，利用环境因子对其进行回归，进而更好模拟林木蒸腾，这时反推求出的γst不仅包括了方程中其他参数在测量或者计算过程中所产生的误差同时也是对于另外那些参数的误差的一个修正[17]，所以对于γst相关性回归的准确程度成为影响方程准确性的最重要因素。

3 结果与分析

3.1 蒸腾速率与气象因子之间的关系

华北落叶松蒸发量日变化过程，研究蒸发量与环境因子之间的相关关系，见图1。由图1可以看出华北落叶松蒸腾速率日变化为单峰型曲线。总的来看，华北落叶松在1 d内的蒸腾速率与温度t、空气相对湿度RH、饱和水汽压差VPD之间存在相关关系：随着温度上升、空气相对湿度下降、饱和水汽压差上升，蒸腾速率逐渐上升，反之，蒸腾速率下降。但又不完全同步，蒸腾速率的变化滞后于气象要素变化1 h左右，07:00左右气象要素发生较大改变，蒸腾启动则发生在08:00左右；在11:00蒸腾达到最强并且持续一段时间，不随气象因素改变而改变；到04:00蒸腾速率开始下降，在23:00左右达到最低值，且保持稳定。蒸腾过程主要发生在白天，夜间蒸腾非常微弱。白天树木冠层蒸发强烈，由蒸腾引起的水分张力在树干木质部内产生上升水柱，土壤中的水分进入根部，使根部形成水势梯度，水分以被动方式进入根部；但是在夜晚木质部的液流则是由根压导致的，水分以主动吸收的方式进入根部[18]，补充水分匮缺，维持植物体内水分平衡，从而导致根系白天吸收的水分要远远大于夜间吸收的水分。

图1 华北落叶松蒸腾速率、温度、空气相对湿度、饱和水汽压差日变化过程Fig.1 Daily variation of transpiration rate, temperature, relative humidity of air and vapor pressure difference of saturated water of Larix principis-rupprechtii

3.2 冠层整体气孔阻力 γst与蒸腾速率之间的关系

γst是林木蒸腾主要的内在影响因素，经过数据处理，剔除可能由于突然的天气变化或者实验仪器设备故障导致的异常数据，采用连续3 d的蒸腾数据，得出γst与林木的蒸腾速率关系如图2所示。两者的相关系数达到0.707 2，说明在观测方法得当环境条件合适的时候γst与蒸腾速率之间关系密切，且呈现负相关关系，在一定的范围内蒸腾速率越快则γst越小。

图2 蒸腾速率与冠层整体气孔阻力的关系Fig.2 Relation between transpiration rate and canopy layer stomatic resistance

3.3 时滞效应

时滞效应是指影响树木蒸腾的气象要素与树干的液流速率并非同步进行，现在测得的环境因子影响的是之后一段时间的树干液流[19]。通常情况下通过茎流计测得的实验数据仅是树木的树干液流而不能代表林冠实际蒸腾，树木液流发生需要滞后一段时间；因此为了客观分析γst对于气象要素的响应机制，精确模拟树木蒸腾以及估算林木蒸腾量，笔者在建立模型之前采用错位对比分析方法进行滞后性分析[20]，如图3所示。利用茎流计数据反推出γst与饱和水汽压差VPD、温度t、大气相对湿度RH分别以10 min的间隔频率进行错位移动，滞前80 min，滞后140 min将错位移动以后的实验数据进行相关性分析，发现饱和水汽压差VPD、温度t、大气相对湿度RH均在滞后70 min时拟合度达到峰值(0.72)，由此可得华北落叶松的树干液流存在非常明显的时滞效应，时滞效应时间为70 min，即树干液流速率变化滞后于饱和水汽压差VPD、温度t、大气相对湿度RH这3个气象因子70 min。笔者之后对于蒸腾的所有研究均为考虑了滞后效应所造成的影响以后得出的结果。

VPD: Vapor pressure difference of saturated water. t: Temperature. RH: Relative humidity of air图3 不同气象因子对华北落叶松树干液流的时滞效应Fig.3 Time delay effect of different meteorological factors on the main flow of Larix principis-rupprechtii

3.4 γst对于环境因子的响应

因为γst主要是由环境因子所决定，受土壤水分补给的影响较小，所以需要分析γst与主要气象因子之间的关系以及受气象因子影响的程度。笔者选取了饱和水汽压差VPD、温度t、大气相对湿度RH这3个主要的环境因子和γst进行相关性分析。由于γst在1 d中的变化非常巨大，采用整天的气象数据回归效果不理想，不能仅用一个方程就表达出γst和环境因子的关系；因此笔者采用分段回归的方法，将1 d分为3个时段(00:00—08:00、08：00—20:00、20:00—24:00)，每1个时段进行一次回归分析，将气象因子作为自变量将γst作为因变量，模拟的结果比较理想。

3.4.1γst对气象因子的单因素回归 冠层的饱和水汽压差影响着蒸腾过程中水汽的传输，是水汽扩散的动力来源，所以要分析γst与VPD之间的关系。通过研究发现，3个时段γst与VPD之间的关系表现为：随着VPD的增加γst逐渐减小，叶片通过自身的气孔调节来保证自身体内水分的动态平衡，同时在1 d中白天植被的蒸腾作用相对较强，VPD相对较大，γst相对较小，而夜间植被的蒸腾作用相对较弱，VPD相对较小，γst则相对较大，这基本符合实际情况。华北落叶松的γst与VPD之间的关系如下图4所示。

γst与温度t之间的关系总体上呈现出随着t的不断上升γst呈现下降趋势，在00:00—08:00夜间这个时段γst与t相关性较低；在08:00—20:00白天的这个时段温度在25 ℃左右，林木蒸腾最强烈，γst达到最低，温度越低，蒸腾越弱，γst则越高；在20:00—24:00这个时段内温度在20 ℃左右γst达到最低。γst与t之间的具体关系如图5所示。

γst与大气相对湿度RH之间的关系如图6所示。由图可知，随着空气相对湿度RH增加，γst逐渐增加，因为RH越高，VPD则越小，相应水汽驱动力很小，水汽传输受到阻碍，γst就变得很大[21]。白天08:00—20:00这个时段空气相对湿度RH在40%～60%范围内γst达到最低值，而在夜间20:00—24:00和00:00—8:00这2个时段内当大气湿度在60%～80%时γst达到最低值。

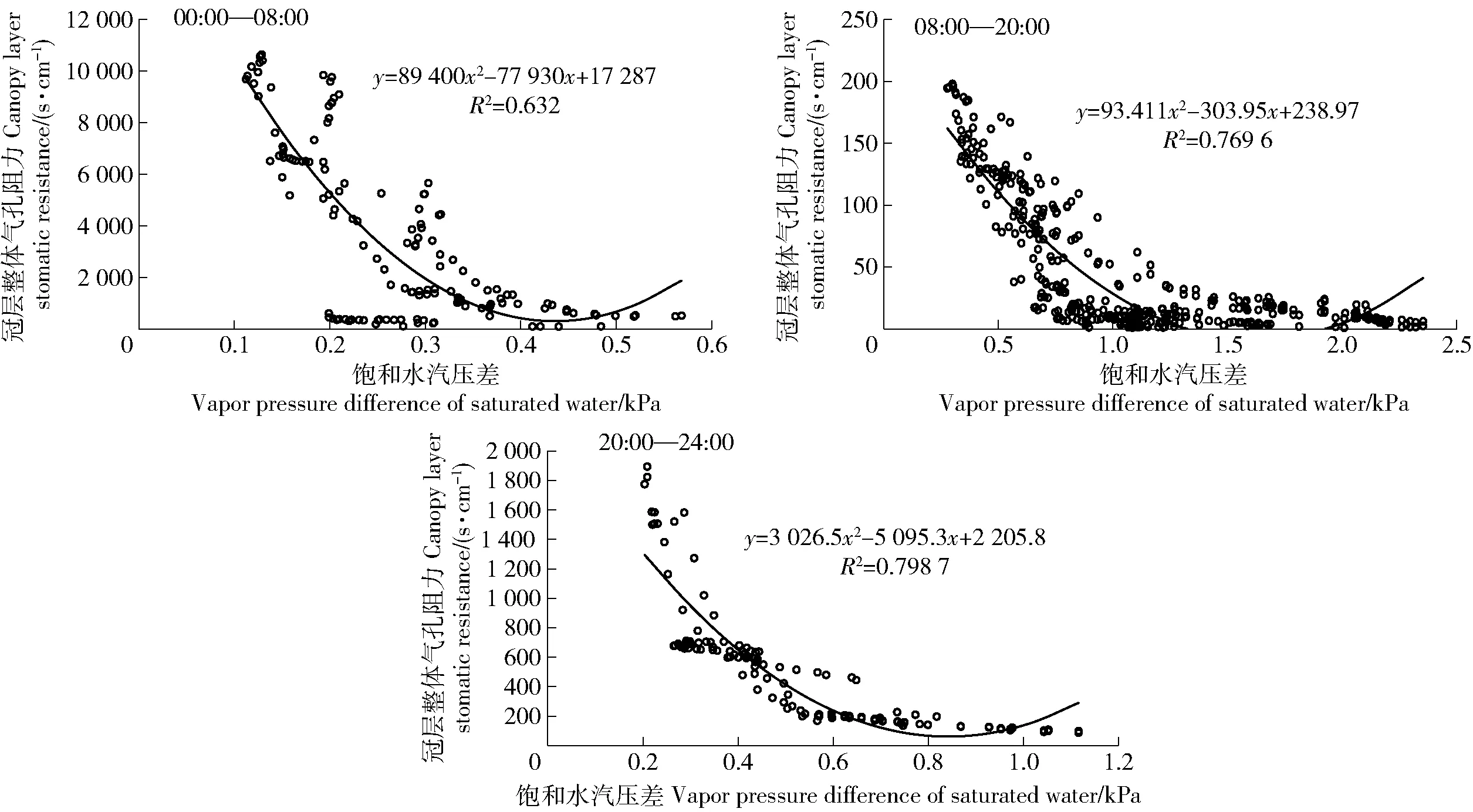
图4 不同时段饱和水汽压差与冠层整体气孔阻力的关系Fig.4 Relationship between the vapor pressure difference of saturated water and canopy layer stomatic resistance at different periods

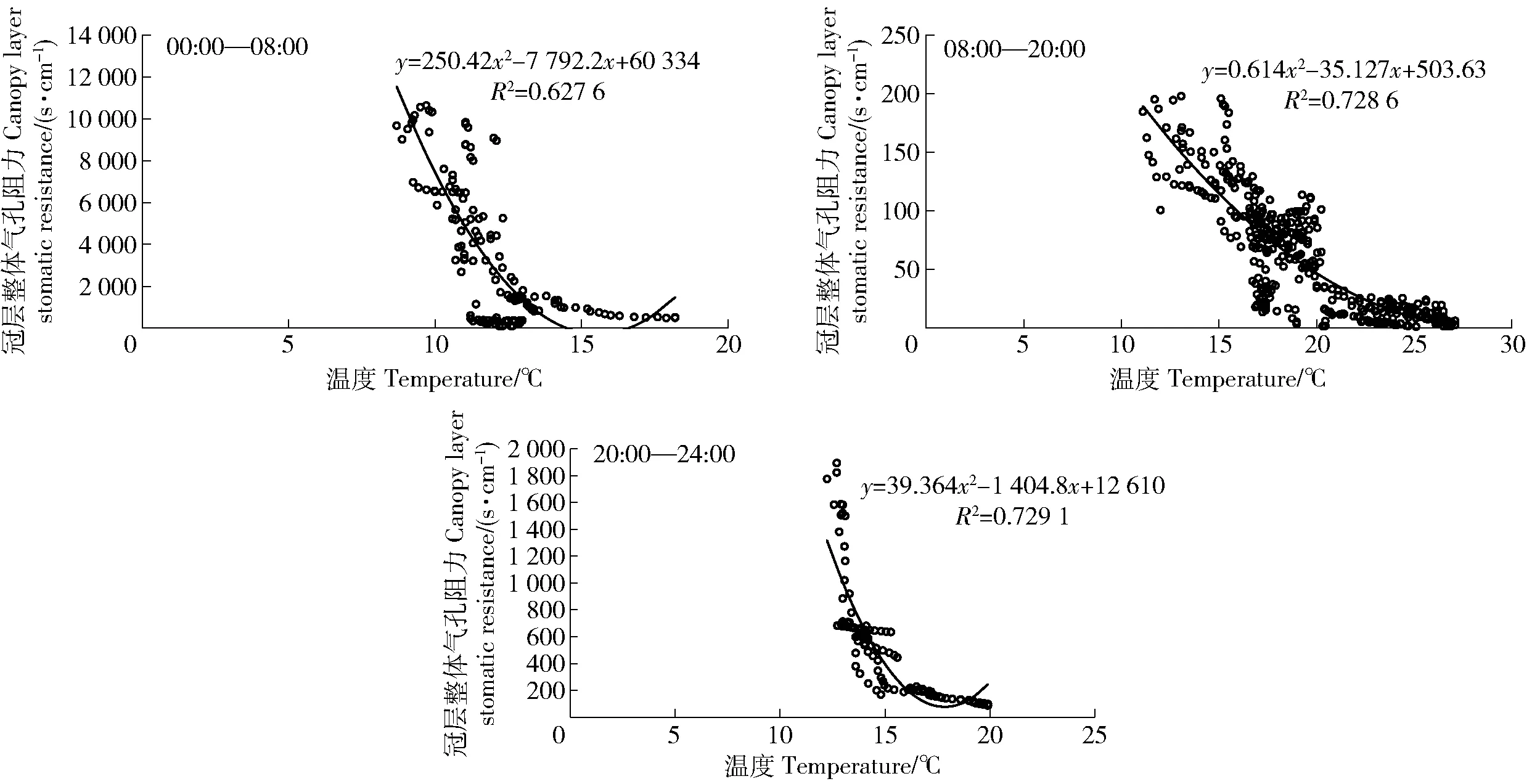
图5 不同时段温度与冠层整体气孔阻力的关系Fig.5 Temperature and canopy layer stomatic resistance at different periods

图6 不同时段空气相对湿度与冠层整体气孔阻力的关系Fig.6 Relative humidity of air and canopy layer stomatic resistance at different periods

3.4.2γst与气象因子的多因素回归γst与主要气象因子回归结果如表1所示。

通过对比发现γst与气象因子的多因素回归相关系数大于单因素回归。这主要是由于γst体现的是水分从植物体内进入大气时需要克服的阻力，受众多环境因子以及植物生理因子的综合影响，因此多因素回归的相关性要大于单因素的回归。此时γst的推算值中包括了P-M模型的其他参数值在求算时产生的误差，同时也可以作为其他参数值误差的修正。γst回归的准确性是影响回归模型模拟结果的最重要影响因素。

00：00—8:00和20:00—24:00两个时段的模拟精度比08:00—20:00时段的模拟精度要差。主要是由于夜间没有太阳辐射，气孔的开闭机制变得复杂，林木蒸腾遵循一定的昼夜节律性[22]，即使气象因子不发生变化，蒸腾仍然按照一定规律进行，导致利用气象因子得出的回归模型在夜间的模拟结果没有白天的模拟结果理想。利用模型我们就可以借助VPD、t和RH 3个气象因子得出一天之内任意时段的林木的γst的近似值。

3.5 模拟结果及验证

3.5.1γst的模拟验证 为了验证所得模型的准确程度，在模拟过程中采用茎流计数据反推γst实测数值来验证模拟与实测的一致性。华北落叶松的00:00—8:00模拟值与实测值的平均相对误差为12.09%，最大相对误差为33.49%；08:00—20:00模拟值与实测值的平均相对误差为10.12%，最大相对误差为23.28%；20:00—24:00模拟值与实测值的平均相对误差为19.58%，最大相对误差为29.27%。模拟值与实测值关系如图7所示。

表1 冠层整体气孔阻力与主要气象因子的回归关系式Tab.1 Regression relation between canopy layer stomatic resistance and main meteorological factors

图7 冠层整体气孔阻力模拟值与实测值的对比Fig.7 Comparison of simulated and measured of canopy layer stomatic resistance

3.5.2 日蒸腾的模拟与验证 利用建立的气象因子与γst的回归模型对P-M方程进行参数矫正，然后对华北落叶松的日蒸腾过程进行模拟验证，采用6月份大通安门滩正常天气条件下样地华北落叶松连续5 d的蒸腾数据来验证模型的精度，通过蒸腾速率的模拟值与实测值的对比，发现蒸腾速率的变化基本呈现相同趋势。均为单峰型日变化，白天时段的蒸腾速率远远大于夜间蒸腾速率。模型的预测结果与实际的蒸腾结果相吻合，拟合度较好，具体的模拟结果如图8所示。

图8 华北落叶松蒸腾速率模拟值与实测值的比较Fig.8 Comparison between simulated and measured transpiration rate of Larix principis-rupprechtii

从表2华北落叶松的日蒸腾的模拟结果中可以看出，模拟值与实测值的累计平均相对误差为12.27%，平均绝对误差为0.12 mm/h，模拟精度基本可行。

4 结论与讨论

研究黄土干旱地区林木的实际蒸腾量，对于提高林木水分利用效率，加强林地植被的建设和管理以及维持林分的稳定有着重要的研究意义。本文以青海省黄土干旱区华北落叶松为究对象，利用探针式茎流计获取的华北落叶松2018年5—8月份生长季的树干茎流的实时数据为基础(10 min频率)，结合P-M方程反推出γst，再利用自动气象站获取试验区的气象数据，分时段构建了高寒区华北落叶松γst与气象因子的回归模型，为准确估算华北落叶松的蒸腾量提供科学参考依据。

任启文等[23]对于华北落叶松的研究发现晴天的蒸腾速率变化与本文研究发现相似为宽峰型曲线，蒸腾速率在10:00—16:00最为强烈，但可能由于立地条件的差异本文研究的华北落叶松在11:00—16:00蒸腾速率保持较高水平。由于树种差异以及干旱胁迫等原因蒸腾速率日变化也可能呈现双峰型，葛亮等[24]的研究发现柑桔树植株的蒸腾速率在一天内的变化呈双峰型曲线，在蒸发特别强烈的中午存在午休现象，植物需要维持自身水分平衡。考虑到气象要素对于不同树种和不同生长阶段的影响，气象要素对于蒸腾速率影响的结论大致相同。蒸腾速率与温度、饱和水汽压差均成正相关，与空气相对湿度呈负相关，这与段汝航等[25]对于湖南会同杉木的研究以及丁访军等[26]对于毛竹的研究一致，仅在相关性上存在一定程度的差异。

对于树干液流和气象因子之间的时滞性分析研究林木蒸腾的基础，Schulze等[27]对于落叶松的研究发现，冠层蒸腾速率达到最大值比测得的树干液流提前约2～3 h；王慧梅等[28]对于兴安落叶松的研究发现，温度和空气相对湿度对于树干液流的滞后效应因季节而异，春季滞后1 h，冬季滞后2 h，在夏、秋2季不存在滞后现象；Phillips等[29]的研究表明，火炬松树木冠层蒸腾的启动时间则提前于树干液流30 min。本文研究发现华北落叶松的树干液流滞后于饱和水汽压差、温度和空气相对湿度70 min。

表2 模拟结果的精度Tab.2 Precision of simulated results

以往对于林木蒸腾的估算研究中，大多以气象因素为自变量建立起与蒸腾的经验预测模型。葛亮等[30]建立了柑桔树植株日间蒸腾的预测模型，模拟结果相对于P-M模型的模拟结果虽然更加接近实测数据；李海光等[31]对华北落叶松的蒸腾仿真模拟就气象因子和蒸腾速率进行了分析,提出了蒸腾耗水的数学模型并应用Matlab软件对华北落叶松进行了模糊蒸腾模型的设计和仿真。但这种方法的地域限制性太大，笔者采用实测数据反推得到真实冠层整体气孔阻力γst，建立起主要气象因子与γst的经验预测模型，结合P-M方程对华北落叶松的日蒸腾过程进行模拟。该方法的夜间模拟效果较差，给结果带来一定的误差，但是这个误差是由P-M方程决定还是模拟过程决定，值得进一步的探讨。所以利用该方法在积累了大量相关基础数据的前提下 ,通过该模型采用主要的气象数据来精确估算林木蒸腾耗水量 ,仍是一种获得满意结果的便捷方法。