基于能量守恒定律的气井井筒携液工况诊断模型

2019-11-12耿新中

天然气工业 2019年9期

耿新中

中国石化中原油田分公司天然气产销厂

0 引言

井筒积液的产生对气井稳产有着较大的不利影响，对于如何诊断井筒中是否存在积液，已有学者提出了不同的方法，主要分为临界流速法[1-12]和临界动能因子法[13-15]。临界流速法理论依据明确，但由于对液滴形状认定不同，模型存在差异，导致计算的临界携液气量差别较大；而临界动能因子法理论依据不明确，且诊断参数来源于实践统计，不同区域统计得到的临界动能因子也不同，导致该方法的应用存在局限性。Turner等[1]提出临界流速法时，指出液滴雾流模型仅适用于液气比小于等于0.000 7 m3/m3的情况，那么，产液量较大的气井，其携液机理是什么，在什么情况下井筒中会产生积液呢？为了解答上述问题，笔者在前期研究[16]的基础上，依据能量守恒定律，建立了新的气液两相垂管流携液工况诊断模型，通过与现场实践、室内实验数据进行比较，对该模型的准确性进行了验证，并采用新模型对某产液气井的工况进行了分析，以期为产液气井的携液工况诊断和积液预防提供理论支撑。

1 携液工况诊断模型的建立

井筒管流中气液两相上行的动力是压力，根据能量守恒定律，气液两相管流能量方程式[10]为：

式中p表示压力，MPa；H表示流向沿程高度，m；ρm表示气液两相混合密度，kg/m3；vm表示气液两相混合流速，m/s；g表示重力加速度，取值为9.81 m/s2；θ表示流向与水平面的夹角；fm表示混相摩阻系数；D表示圆管直径，分别表示总压能损失项、动能变化项、势能变化项和摩阻损失项，Pa/m。

气井井筒单位高度差的压降很小，气相、液相流速的变化也很小，因此动能变化项近似为零，且对于垂管流，sinθ=1，则式（1）近似表示为：

1.1 段塞流—过渡流临界携液工况诊断

积液的本质表现是气相不连续[16]，两相流型为气泡流或段塞流。因此，产生积液的临界工况应该是两相流型由气相不连续的段塞流向气相连续的过渡流转化时的临界点。如果该临界点出现在井底，井筒内不会存在积液。

在临界工况下，气液两相互不携带，在压力的驱动下以各自的速度上升。由于管流中流体的流速在径向上存在差异[17]，受气体滑脱效应的影响，沿管壁会存在液相环膜，混相体系受到的摩阻仅仅表现为液相与管壁间的摩阻。在临界工况下混相能量方程式为：

式中p0表示混相压力，MPa；λc表示临界持液率；ρg、ρl表示气相、液相密度，kg/m3；f 表示油管摩阻系数；vls表示液相实际流速，m/s。

以λh表示规则环膜的持液率，则气相段塞的最大直径为，临界工况下气相能量方程式为：

式中pg表示气相压力，MPa；fg表示气相阻力系数；vgs表示气相实际流速，m/s。

气相段塞上行受到两种阻力，一种是由气液相间速度差引起的剪切摩阻，另一种是上覆液相的重力。在临界工况下，上覆液相的重力等于气相对液相施加的速度压力，即

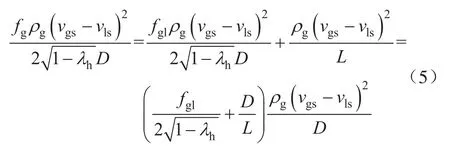
式中fgl表示气液相间剪切摩阻系数；L表示气相段塞长度，m。

在管流中，不论流型如何，不同截面之间气相与混相的压力差都是相等的[10]。将式（5）代入式（4），再与式（3）合并，得

由气体状态方程推导得

式中γg表示气体相对密度；Z表示气体偏差因子；T表示温度，K。

临界携液气量计算式为：

式中Qgc表示临界携液气量，104m3/d。

将式（7）、（8）代入式（9），得

由式（10）可知，L越小，Qgc越小，而气相段塞刚刚充满管流横截面时L最小。受压差和速度压力的挤压，气相段塞为不规则椭球形气泡。方便起见，L近似取气泡处于两种极限状态（规则球体和圆柱体）的平均高度，则有

考虑持液率，vls的表达式为：

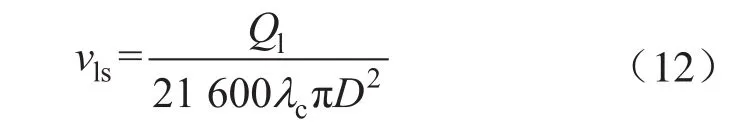
式中Ql表示液相产量，m3/d。

将式（11）、（12）代入式（10），得

式（13）则为临界携液气量的计算式，其中fgl、λc和λh的确定如下：借鉴本文参考文献[18]，将fgl取值为0.014 2；液相不发生沉降聚集时最大持液率为0.215[19]，该值可以作为λc的取值；对于管壁液相环膜，气相仅通过相间剪切摩擦对其进行举升，可以认为L无限大，管流持液率等于λh。当液量很小时，即，同时结合动能因子的定义[10,13]，对式（7）进行简化，得

式中vgc表示气相临界携液流速，m/s；Fgc表示临界动能因子，Pa0.5。

由实践统计得Fgc介于8～10 Pa0.5[13-14]，不同临界流速法模型对应的Fgc介于5～21 Pa0.5[15]，取ρl为1 074 kg/m3，由式（14）计算不同D（取值为40.0 mm、50.7 mm、62.0 mm、76.0 mm）和Fg（取值介于5～21 Pa0.5）下的λh，如图1所示，计算的λh均小于0.008。因为λh很小，可近似取值为0。

图1 环膜持液率与动能因子关系曲线图

将 fgl、λc、λh的取值代入式（13），得

式（15）则为临界携液气量的计算式，可以用于诊断井筒中是否产生积液。

1.2 过渡流—波浪流流型探讨

在连续气相出现之前流型为段塞流，在连续气相出现以后，井筒携液连续，采用临界流速法判断则认为此时两相流型是环雾流。因此，式（10）中的L为无限大，环膜持液率λh接近于λc，将λh、λc均取值为0.215，再代入式（7）、式（13），得

与式（15）进行对比，Qgc大幅增加，即由段塞流向环雾流转变的瞬间，临界携液气量将产生巨大变化，这显然是不合理的。因此，在段塞流和环雾流之间，还存在一种流型——波浪流。此次采用新模型，对连续气相出现后的流型进行探讨。

1.2.1 波浪流携液模型的建立

受气液界面张力的作用，波浪流中液相将向管壁自然回缩，受液相的影响，气相迎流面积大幅减小，而液相受到的气相速度压力施加的举升力也会减小；受径向上流速存在差异的影响，波浪的流速及作用在波浪上的气相流速也不等同于管流的平均流速；在气芯的拖拽下，从液相波峰上会不断分离出液滴，同时气芯中的液滴也受到径向上流速差异的影响而不断偏向、沉降、汇入波浪[16,19]。

假设波浪流为规则的环形波浪，管流的混相能量方程式为：

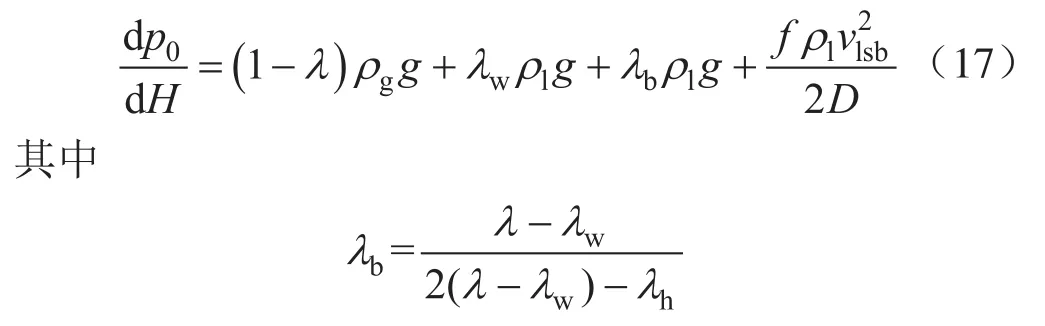
式中λ、λw分别表示管流、液滴持液率；λb表示环形波浪持液率；vlsb表示波浪实际流速，m/s。

夹带液滴的气相能量方程式为：

式中vgsb表示波浪迎流面气相实际流速，m/s。

由于受液相的影响，气相迎流面积减小，有

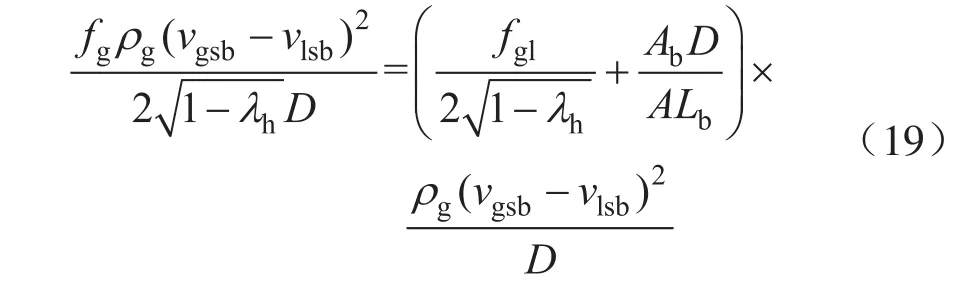
式中Ab表示波浪迎流面积，m2；A表示气相最大截面积，m2；Lb表示波长，m。

将式（19）代入式（18），然后与式（17）合并，得

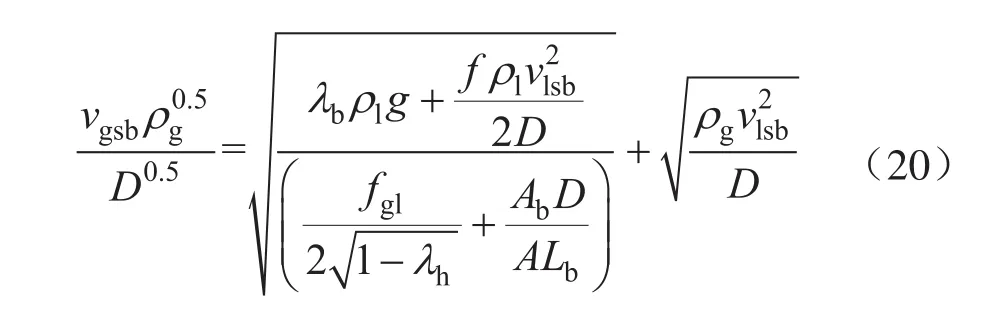
采用式（20）进行计算，必须确定Ab、A、Lb、vlsb的数值，下面分别进行讨论。

对于规则波浪，Ab、A的计算式为：

在界面张力和重力的共同作用下，波浪近似为半圆形。设波峰距管流中心的距离为r，有

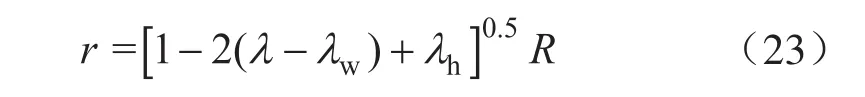
式中R表示圆管半径，m。

Lb计算式为：

式中Qlb、Qlw分别表示波浪与液滴的流量，m3/d。

根据管流流速基本公式[17]，波峰气流流速与气相实际流速的关系式为：

式中vgsr表示波峰气流流速，m/s。

将式（23）代入式（26），有

借鉴平均流速为最大流速的0.817倍[17]，考虑vgsb为vgsr的0.817倍，有

用 λ代替 λc、vgsb代替 vgs、vlsb代替 vls，Lb代替 L，将式（25）代入式（20），再代入式（9），得

式中Qgb表示波浪流携液气量，104m3/d。

式（29）则是波浪流携液气量计算式，利用该式可以计算不同持液率和液量下波浪流的携液气量。

1.2.2 过渡流的形成

连续气相刚出现时，λ=λc，取值为0.215，相对于λ，λw和λh都很小，均可取值为0。代入式（29），推导可得

式中Qgcb表示波浪流携液临界气量，104m3/d。

与式（15）对比，可知Qgcb明显大于Qgc。这是因为，环形波浪的持液率较大，势能压降大幅增大，需要更高的气量来遏制液相的减速积聚，由段塞流到波浪流，之间还存在一个过渡状态。这就从理论上解释了过渡流的客观存在、形成机理与数值界限。

1.3 积液诊断模型对比

设置 ρl为 1 074 kg/m3、γg为 0.65、T 为 373.15 K、Z为1.0、D为62.0 mm、f为0.015 12[10]，采用式（15）计算不同压力、不同液量下的临界携液气量，并且与临界动能因子法[16]和Turner模型——临界流速法的计算结果进行对比。如图2所示，液量较小时，采用新模型计算得到的临界携液气量接近于临界动能因子法[16]计算的临界携液气量，明显低于Turner模型的计算结果，这与实践中发现的“在低压小液量井上采用Turner模型的计算结果明显偏大”的现象一致。随着液量增大，采用新模型计算得到的临界携液气量逐渐增大，并且压力越高，临界携液气量增大越明显。这就解释了实践中发现的“在高压大液量气井上，即便产气量高于Turner模型的计算结果，井筒中也会产生积液”的原因。

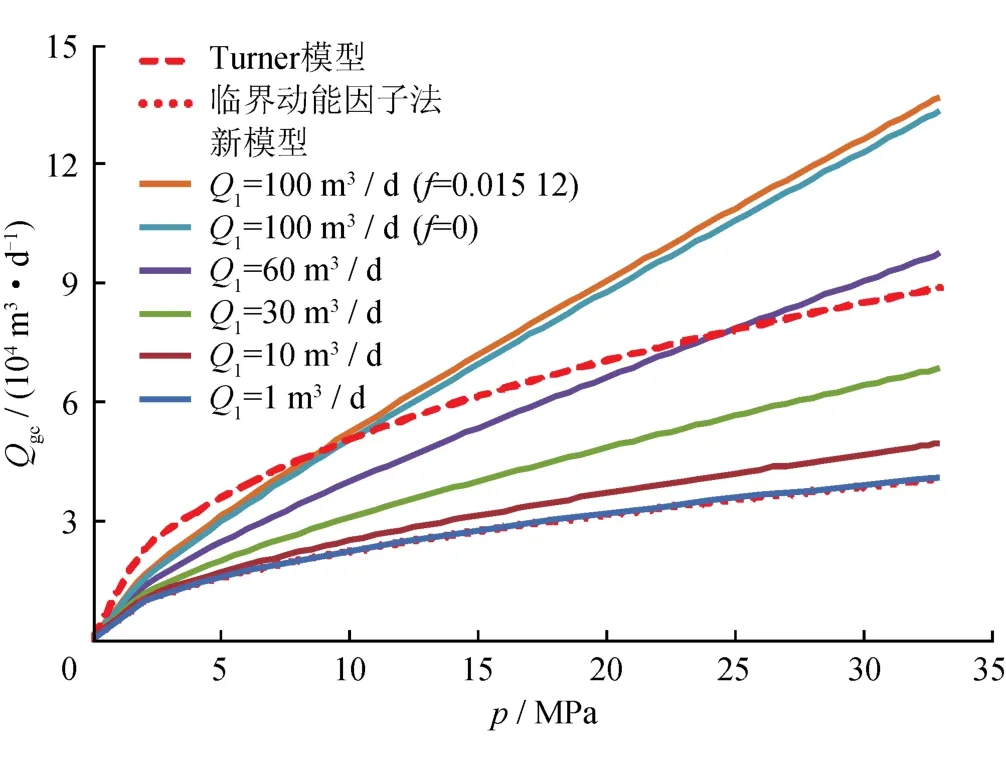
图2 临界携液气量与压力、产液量关系曲线图（62 mm管径）

根据Turner模型，临界携液气量与圆管直径（D）的2次方成正比，因此小油管成为一种重要的排液采气工艺。但实践表明，小油管应用在大液量气井上往往达不到预期的排液采气效果。应用新模型可以得到以下解释：①由式（15）可知，由新模型计算得到的临界携液气量除了与管径（D）有关，还与液相产量（Ql）和油管摩阻系数（f）有关，低液量下，近似与管径的2.5次方成正比，小油管排液采气效果更明显；②更换小油管后，虽然临界携液气量会降低，但随着液量增大，其降幅越来越小，更换不同管径小油管获得的临界携液气量降幅也越来越接近，采用小油管进行排液采气的优势越来越不显著（图3）；③摩擦阻力不是小油管在大液量气井上应用效果差的主要影响因素。以日产液量100 m3为例，计算不考虑摩擦阻力情况下的临界携液气量，其值与考虑摩擦阻力情况下的计算结果非常接近（图2）。

图3 油管直径变化后临界携液气量降幅对比图

2 气液两相垂管流携液机理

垂管流气液两相上行依靠的是压能驱动。气液两相垂管流的流型可分为以下5种：气泡流、段塞流、过渡流、波浪流、环雾流（图4）。当气量较低时，气相分散在液相中，流型为气泡流或段塞流，气液两相在压能驱动下上行，气相在液相浮力作用下加速上行。随着气量增大，相邻气泡接触合并，出现连续气相，液相向管壁回缩，趋于形成波浪流；因为波浪受到的速度压力小，又有重回连续液相的趋势，流型表现为不稳定连续携液的过渡流，气相开始对液相产生携带作用。随着气量进一步增大，回缩到壁面的液相受到的气相举升力增大，液相被气芯拖拽，不断分离出液滴，而气芯中的液滴，又会持续偏向、沉降、汇入波浪[16,19]，此时流型呈现为气芯中包含液滴的波浪流，气相对液相的携带作用增强。随着气量的持续增大，气相速度压力增大，波浪加速上行，波峰逐渐减小，直至形成规则环膜与气芯中的液滴共存的环雾流，气相对液相的携带作用进一步增强。当液量很小、气量很大，环膜的液滴分离效应总是强于气芯中液滴的偏向沉降效应时，环膜无法保持，才形成纯粹的雾流。纯粹的雾流只是环雾流的零液膜特例。

图4 两相垂管流流型变化示意图

3 模型验证与实例分析

3.1 现场实践统计

当液量很小时，式（15）可以简化为：

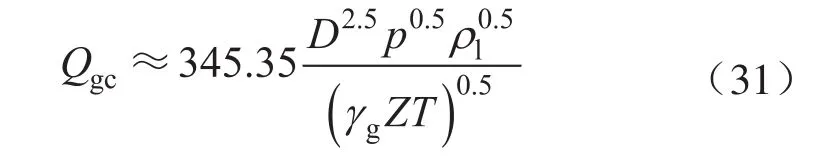
将式（31）代入式（9），得

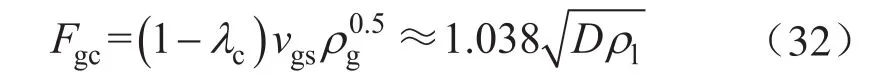
临界动能因子是一个受多种因素共同影响的变量。当液量较小时，近似仅与液相密度和管柱直径有关。若 ρl介于 1 000～ 1 150 kg/m3，由式（32）可计算得到：D为50.6 mm时，Fgc介于7.38～7.92 Pa0.5；D为62.0 mm时，Fgc介于8.17～8.76 Pa0.5；D为76.0 mm时，Fgc介于9.05～9.70 Pa0.5。

依据现场实践统计，D为62.0 mm时，Fgc为8.26 Pa0.5[13,16]；D 为 76.0 mm 时，Fgc为 9.60 Pa0.5[14]。可见，新模型计算结果与现场实践统计数值很吻合。对于同一气藏而言，液相密度接近，若选用的油管规格也一样，则临界动能因子就近似为常数。这就从理论上解释了在同一区域，通过实践统计得到的临界动能因子近似为常数，而在不同区域，统计结果存在差异的原因。

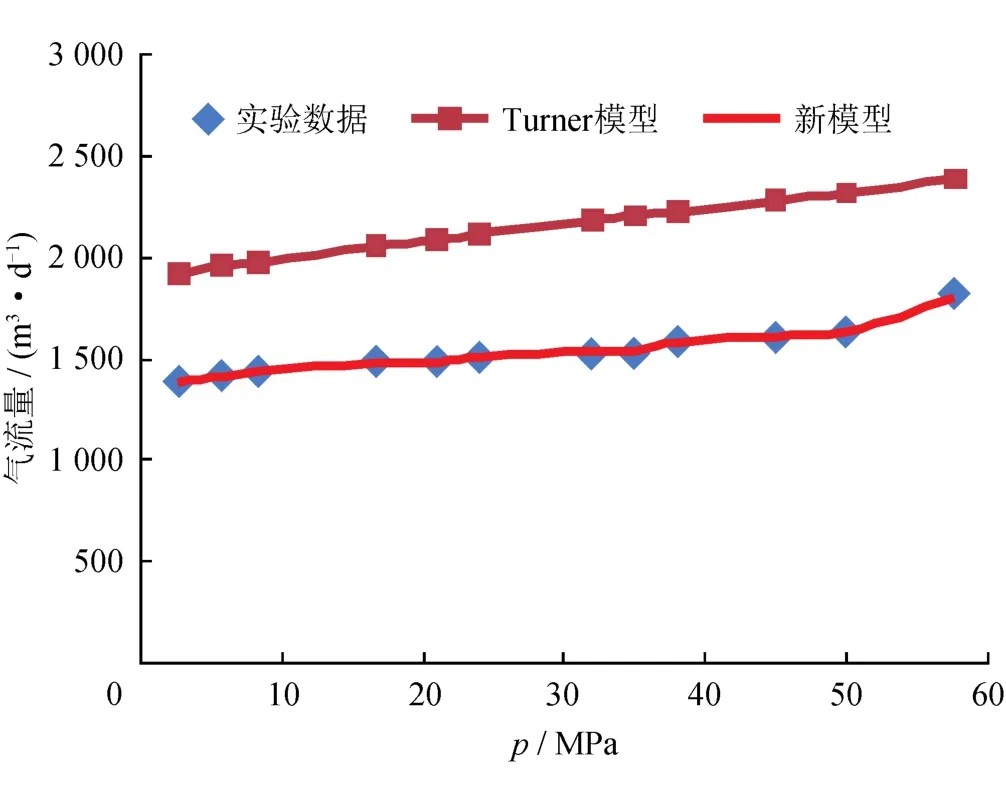
图5 不同模型计算结果对比图（低液气比气井积液可视化实验）

3.2 室内实验

为探究两相垂管流的携液机理，已有学者开展了相关室内实验研究，其中典型实验包括低液气比气井积液可视化实验[9]和高液气比气体携液的液体临界含量实验[11]。根据实验数据，应用笔者提出的新模型进行如下分析。

3.2.1 低液气比气井积液可视化实验

实验管柱直径为40 mm，液气比小于0.000 1。观察管柱出口出液情况，当管壁刚刚出现液膜（vls≈0），可以认为管内流型是环雾流，L无限大。根据实验参数，由式（14）计算λh，考虑气芯中液滴的影响，用 (λh+0.000 7)代替 λc，由式（7）、（10）推导出环雾流携液临界气量计算公式，如图5所示，新模型计算结果与实验获得的数据基本一致，平均误差仅为0.35%。

3.2.2 高液气比气体携液的液体临界含量实验

实验管柱直径为50 mm，控制注入气量使其略高于Turner模型计算的临界携液气量，通过改变注入液量，分析两相垂管流中气相的携液能力。将相关参数分别代入式（15）、（29）、（30）计算，结果显示，新模型计算得到的波浪流携液气量Qgb与实验气流量基本一致，平均误差仅为3.71%（图6），两相流型为波浪流。

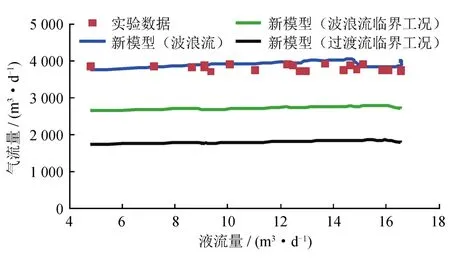
图6 不同模型计算结果对比图（高液气比气体携液的液体临界含量实验）

3.3 实例井分析

因边水侵入，某气井大量出液，如图7所示，产液量由7 m3/d逐渐上升，最高达69 m3/d，而产气量逐渐降低，油套压差逐渐增大，井筒积液的影响越来越大。该井产气量一直低于Turner模型计算的临界携液气量，后期甚至低于李闽椭球模型计算的临界携液气量，但仍然能够携液生产，应用这两种模型都无法对该井的生产现象进行合理的解释。此次，应用新模型分析解释认为：①阶段Ⅰ（1～11 d），产液量较小，油套压差缓慢增大，产气量明显高于由式（30）计算的井底处波浪流携液临界气量，两相流型属于环雾流—波浪流，携液稳定，实测井筒下部流压梯度介于0.15～0.18 MPa/100 m；②阶段Ⅱ（12～23 d），产液量增大但相对稳定，油套压差增幅较大，表明井筒持液率升高，但产气量接近于井底处波浪流携液临界气量，两相流型属于规则波浪流，携液稳定；③阶段Ⅲ（24～37 d），产液量逐渐增大，油套压差也逐渐增大，产气量逐渐降到式（15）计算的井底处临界携液气量，两相流型属于过渡流，实测井筒下部流压梯度介于0.23～0.25 MPa/100 m；④阶段Ⅳ（38～70 d），产液量、油套压差、井筒持液率持续增大，产气量逐渐降到式（15）计算的井口处临界携液气量，在井筒上部，两相流型属于过渡流，在井筒下部，两相流型属于段塞流，实测井筒下部流压梯度介于0.31～0.54 MPa/100 m；⑤阶段Ⅴ（71 d以后），产液量达到峰值后逐渐降低，油套压差趋于平稳，产气量低于式（15）计算的井口处临界携液气量且持续下降，两相流型为段塞流、气泡流，实测井筒下部流压梯度介于0.79～0.92 MPa/100 m。