参考值范围样本量估计中参数的适度性研究

重庆医科大学公共卫生与管理学院/医学与社会发展研究中心/健康领域社会风险预测治理协同创新中心(400016)

夏万元 钟晓妮 陶 浩 陈 茜 赖敏清 田考聪△

【提 要】 目的 探讨Troendle和Jennen-Steinmetz提出的参考值范围样本量计算方法的适用条件及参数合适取值范围。方法 通过计算机模拟，研究样本量计算方法的可用性和相关参数变化时样本量的变化情况。结果 Jennen-Steinmetz提出的样本量计算方法中模拟计算的统计量η能较好满足研究设计的精度要求，容许误差δ小于0.003时，估计样本量出现迅速上升。Troendle的标准中新构建统计量r小于0.02时，样本量需求出现迅速上升。根据模拟样本量估计结果，我们认为参数δ和r的适宜取值范围分别为0.002～0.015和0.01～0.12。结论 当前样本量计算方法能一定程度上解决参考值范围计算时样本量估计问题。但是该方法还需要进一步完善改进。

国内外的统计学家及医学专家都提出了一系列的参考值范围估计方法以及校正方法[1-3]。但是对于制定参考值范围需要的样本量却鲜有提及。在国内，有研究者在研究多元参考值范围的估计时提出了样本量不应小于100的标准[4]。1987年Linnet等[5]针对正态分布和对数正态分布提出了相应的样本量标准，但是并未给出具体的样本量估计公式。另外，在2003年Troendle等[6]的研究中针对正态分布资料的双侧参考值范围提出了一种可调标准。2005年Jennen-Steinmetz[7]在Linnet的基础上对一种新的样本量估计方法进行探索，该方法对于单侧和双侧的参考值范围样本量估计均适用。

本文主要对Troendle和Jennen-Steinmetz提出的参考值样本量估计方法的适用条件以及参数取值范围进行探索和讨论。并在此基础上对参考值范围样本量计算方法的研究提出一些思考。

样本量计算公式

Jennen-Steinmetz在2005年提出了一种参考值范围样本量估计方法，根据样本量估计方法中参考值范围界值之外的人群比例(ψs)满足指定的容许误差δ的要求进而推导出相应的样本量估计公式。

基于参数方法的样本量估计公式

(1)

(2)

基于非参数方法的样本量估计公式

n=((1+q)(1-q)/4)(z(1+η)/2/δ)2

(3)

n=q(1-q)(z(1+η)/2/δ)2

(4)

Troendle在2003年的研究中根据分位数的90%置信区间宽度和参考值范围之间的比例，确定了一个针对于正态分布双侧参考值范围的一般标准。

Troendle的研究中对于正态分布双侧参考值范围的一般标准公式为

(5)

公式中各个参数的解释：

n指所需样本量；zg、z(1+η)/2、z(1+q)/2和z(1-q)/2为正态分布下，其对应的临界值；q指参考值范围的百分数；φ(z(1+q)/2)和φ(zq)为标准正态分布下对应的密度函数值；η为ΨΩ与ψs差值小于等于容许误差δ的概率(即P{|ΨΩ-ψs|≤δ}=η，ΨΩ：指总体中参考值范围理论上界或下界之外的人群所占的比例(单侧时为1-q，双侧时为(1-q)/2)，ψs：指总体中在实际样本参考值范围的上界或下界之外的人群所占的比例)；δ为ΨΩ与ψs之差的最大可接受值；r指端点分位数的90%置信区间宽度和参考值范围宽度之间的比例。

研究方法

在Jennen-Steinmet的估计方法中η是一个核心参数，它在实际抽样中的大小可以帮助我们判断该样本是否符合研究设计的精度要求。故本文中的计算机模拟是对Jennen-Steinmetz的估计方法中η在真实研究时能达到的估计值进行计算机模拟估计。

计算参考值范围所需样本量大小取决于参考值范围的宽度q、η和容许误差δ。这三个值均可在研究设计之初，根据医学指标的专业特性和统计学原则指定，进而估计研究所需的理论最小样本量。本文在模拟过程中按照该理论样本量抽出的样本情况与总体间的差异能否满足设定误差δ的概率为η。计算机试验通过多次模拟抽样从而估计出实际抽样能达到的η值。

根据参数η和δ在其理论取值范围内，进行等距取值，计算相应情况下样本量。根据样本量的变化情况来探索两个新参数在不同情况下的合适取值范围。此外，本文还采用SAS宏和R函数形式对相应的公式进行编译，便于研究者计算使用。

计算机模拟思路

1.正态分布的模拟：

由于一般正态分布均可转化为标准正态分布，故参数分布采用标准正态分布作为抽样总体进行模拟。

以下为计算机模拟步骤：

(1)根据各个参数的设定值，按照参数方法的样本量估计公式，估计需要的最小样本量

(2)按照估计的最小样本量，在标准正态分布下随机抽样

(3)根据抽样结果算出相应的参考值范围界值

(4)估计界值之外的人群所占的比例(ψs)

(5)差值|ΨΩ-ψs|为该样本的抽样误差

(6)若差值的绝对值小于δ，则记为1

(7)统计1000次试验结果为1的次数，这个次数除以1000即为η

(8)重复3～7个步骤100次，计算η的平均值，即为最终的η

2.非正态分布的模拟：

非参数采用样本量公式推导时使用的是次序统计量的分位数估计。由于次序统计量的分位数分布服从参数为(n+1)(1-q)和n+1-(n+1)(1-q)的Beta分布[8]，所以模拟时直接按样本量和分位数在对应的Beta分布下抽样，抽出的数值即为真实世界中一次抽样中样本参考值范围界值之外的人群所占总体人群的比例(ψs)。

以下为计算机模拟步骤：

(1)根据各个参数的设定值，按照非参数方法的样本量估计公式，估计需要的最小样本量

(2)按照取定的q和最小样本量n的值用对应的Beta分布B((n+1)(1-q)/2,n+1-(n+1)(1-q))进行模拟(区间对称时，在分布B((n+1)(1-q)/2,n+1-(n+1)(1-q)/2中抽取一个随机值(即为：ψs))

(3)差值|ΨΩ-ψs|为该样本的抽样误差

(4)若差值的绝对值小于δ，则记为1

(5)统计1000次试验结果为1的次数，这个次数除以1000即为η

(6)重复2～5个步骤100次，计算η的平均值，即为最终的η

结 果

表1是根据Jennen-Steinmetz在2005年提出的样本量估计方法(公式：(1)、(2)、(3)、(4))，根据不同的参数q、η和δ在不同假设值情况下所需的样本量并通过模拟试验估计出的实际η。结果显示，在各个参数的不同水平取值下，模拟抽样中的η与估计公式中的预设值都比较接近甚至能超过预设值的要求。最小样本量除了受到容许误差δ的影响外，还受到q、参考值范围的单双侧和估计方法的影响。当q的取值从0.90变化到0.95，其他参数和情况相同时样本量的增加量基本在一倍左右。在其他参数相同时，参数方法与非参数方法相比或单侧参考值范围与双侧参考值范围相比，其样本量的变化情况也类似。

图1为根据Jennen-Steinmetz在2005年提出样本量估计方法(公式：(1)、(2)、(3)、(4))，在预设η为0.9，q为0.95时。不同的容许误差要求(即：δ的不同取值情况)下样本量需求的变化情况。针对相同的容许误差非参数方法相对于参数方法而言会较大地增加样本量的需求。参数单侧和非参数双侧的样本量变化趋势基本一致。在δ小于0.003时，最小样本量随δ的变小迅速增大。

表2是根据Troendle(公式(5))在2003年提出的标准中r在不同取值情况下估计目的指标0.90，0.95和0.99参考值范围所需要的最小样本量。本文估计了r取值从0.01到0.5的理论样本量估计情况，考虑到实际工作中可能涉及的样本量范围的合理性，罗列了其中的一部分。从结果中可以看出，r>0.16时样本量均小于一般推荐值(一般推荐样本量不应小于100[4])。r<0.03时，随着r的进步缩小，样本需求迅速增大。

表1 参数q、β和δ在不同取值情况下的样本量需求及其模拟η

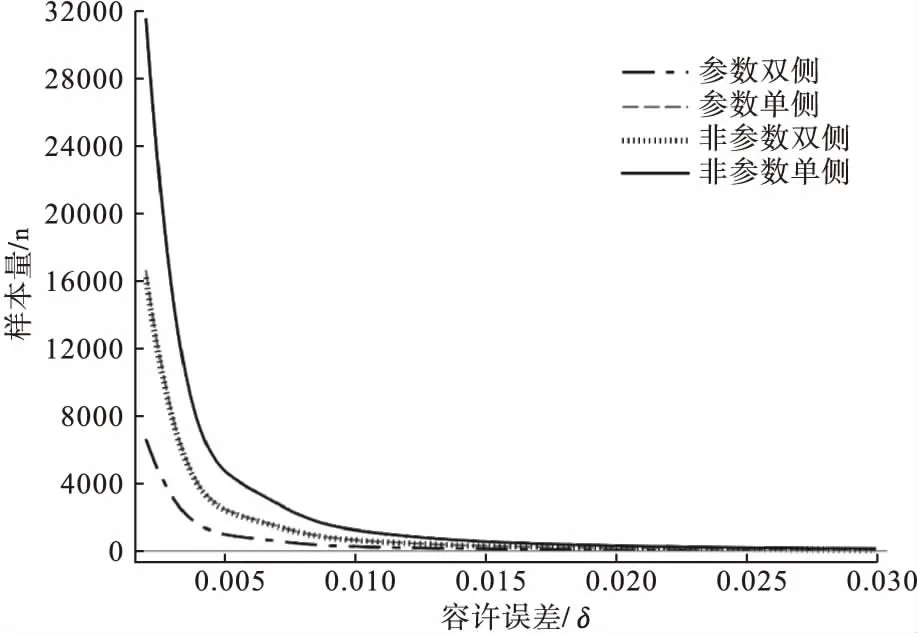
图1 不同的容许误差(δ)要求下样本量需求的变化情况(固定η=0.9，q=0.95)

表2 r不同取值情况下所需要的最小样本量

图2为参考值范围样本量估计时需要考虑的一般流程，主要分为两个方面，一方面是需要指定的参考值范围是单侧还是双侧。另一方面是研究的指标分布类型是否为参数分布。确定这两方面的情况后，即可确定相应的样本量估计公式。再根据公式确定相应的参数取值(r或q、δ和η)进行估计。我们在附件程序中提供了公式(1)～公式(5)估计的SAS和R程序，供读者参考。

图2 参考值范围样本量一般估计流程

讨 论

模拟验证结果显示通过重复抽样计算的η基本能达到所计划的预设值。在变换参数δ和r的计算中，我们计算了δ在0.001～0.03取值时其相应的样本量在8～32000变化，r在0.01～0.30取值时其相应的样本量在20～23523变化。结合实际科研工作中合理的样本量范围，建议δ的适宜取值范围约在0.002～0.015。r的适宜取值范围约在0.01～0.12。

根据图1结果，我们对不同情况下Jennen-Steinmetz的公式中参数的取值范围进一步讨论，参数单侧和非参数双侧的样本量变化在容许误差大于0.001时样本量迅速下降，而小于0.003时需要的样本量迅速增大。建议一般情况下容许误差的选取可在0.3%～1%。参数双侧的样本量在容许误差大于0.75%时样本量迅速下降，在小于0.2%时需要的样本量迅速增大。建议一般情况下容许误差的选取可在0.2%～0.75%考虑。非参数单侧的样本量在容许误差大于0.75%时样本量迅速下降，在小于0.2%时需要的样本量迅速增大。建议一般情况下容许误差的选取可在0.2%～0.75%。建议研究者可根据研究的实际要求，在此区间选择合适的误差容许范围。η是估计样本量时构建的一个新统计量，暂时没有标准的取值范围，一般情况η取0.9，但在实际研究过程中如果研究需要或者条件有限，可适当调整η的取值，但不应该低于0.8。另外，参考相关统计学教材[9-10]，q的取值一般为0.9或0.95。陈彬[4]等在相关研究中指出q的取值应不低于0.8。

对Jennen-Steinmetz方法的模拟结果中可知。在参考值范围的研究过程中，应结合实际情况选取合适的参数，对于能转换为正态分布的指标，应转换后再进行样本量估计和参考值范围估计。此外应结合研究的实际可行性确定合适q和δ值以及其他影响因素，以期望指标能尽可能真实地反应“正常”人群当前的情况。

Jennen-Steinmetz法也有一些不足的地方，医学研究的样本量估计思想一般是在统计假设的基础上为满足统计的准确性和可靠性来进行估计，但Jennen-Steinmetz研究并未考虑相关的统计假设，而是通过参考值范围界值之外人群比例(ψs)的计算来估计样本量。导致公式中的相关指标η难以用经典的统计标准解释。增加了公式的理解难度。此外，在双侧参考值范围计算时根据参考值范围的对称性，文中的公式仅考虑了一侧的参考值范围界值之外的人群比例。但由于抽样误差的存在这个范围宽度是不对称的。所以该公式可能低估双侧参考值范围的样本需求量。

Troendle提供的参考值范围样本量需求的一般标准(即公式5)是使用参考值范围端点值的90%置信区间长度与参考值范围的长度的比值构建了一个新的统计量r。然后根据研究的精度要求对r的取值规定估计出所需的样本量n，需要注意的是r并非一个随机变量，不会因为抽样不同而改变。该方法要求参考值范围要为双侧对称。此方法并不适用于单侧参考值范围样本量需求的估计。此公式在构建统计量r时，只考虑到了样本本身的情况，并没有很好的度量样本数据与总体之间的抽样误差。此外，该方法估计的样本量是能使样本参考值范围端点值的90%置信区间长度与参考值范围的长度的比值小于预设的r值的确定样本量，但并非最小样本量。即按照该样本量进行随机抽样的样本，所估计的比值必然小于r。另外，端点值90%置信区间长度，只是取了常用的90%置信区间，如果取其他置信区间长度时计算公式将会随之变化。因此，本文并未对Troendle的公式进行计算机模拟。

与Troendle的估计方法相比，Jennen-Steinmetz的估计方法引入了抽样误差的概念。并且更好地解释了样本和总体之间的关系，但其参数多，估计相对繁琐，而Troendle的估计方法相对来说更加简单。如果研究者已知指标的总体分布，不需要细致地衡量抽样误差或研究结果只需要在小范围内使用，则可以采用Troendle的样本量估计方法。如果所研究的指标分布未知、需要制定单侧参考值范围、容易产生抽样误差或研究结果需要在较大范围内使用，则应该采用Jennen-Steinmetz的估计方法。

值得注意的是文中介绍的公式均只考虑了单一因素的参考值范围的样本量估计，对于采用回归进行的参考值范围估计或需要调整其他协变量的影响时，以上方法并不适用。此外，文中的方法均未使用任何样本信息，这可能会低估变异很大的指标在计算参考值范围时实际所需要的样本量。综上，当前的参考值范围样本量计算方法能为科学研究提供一定的参考，但还需要进一步的研究进行改进优化，制定更完善的样本量估计方法。