鼠疫传染病优化算法*

黄光球，陆秋琴

西安建筑科技大学 管理学院，西安 710055

1 引言

群智能优化算法[1]求解具有大量局部最优解优化问题的全局最优解具有独到的优势。当此类算法求解一个优化问题时，同时启动很多试探解实施迭代计算，这种“群起而攻之”的方法可求解一些非常困难的多局部最优解优化问题。然而不幸的是，不存在一种群智能优化算法可求解所有类型的优化问题[2]。迄今为止，人们已提出很多已被广泛应用的群智能优化算法，如遗传算法[3]、蚁群算法[4-5]、粒子群算法[6-8]、生物地理学算法[9]、差分进化算法[10-11]、蜂群算法[12]等。

在群智能优化算法中，每个试探解被比喻成具有生物特征的个体。于是，一些特殊生物活动场景被用来构造群智能优化算法[3-4,8,12]。然而，目前已提出的群智能优化算法所源于的生物活动场景都很简单，且其数学基础较弱，如遗传算法、蚁群算法、生物地理学算法、蜂群算法等。有的群智能优化算法甚至没有生物活动场景，如粒子群算法和差分进化算法等。如果一个群智能优化算法具有明确的较生动的生物活动场景，且该场景能够用数学理论精确描述，那么该场景极有利于构造群智能优化算法，因为该群智能优化算法奠定在很好的数学基础上，其性能易于被分析。本文提出的鼠疫传染病优化算法（plague infectious disease optimization，PIDO）正是基于这样的生物活动场景。

鼠疫是鼠疫耶尔森菌借鼠蚤传播的烈性传染病[13]，致死率极高，人类历史上曾三次大流行，为广泛流行于野生啮齿动物间的一种自然疫源性疾病。为了控制鼠疫的危害，全世界花费了巨大的努力，构建了大量数学模型来研究鼠疫的传播机制。主要表现在如下四方面：

（1）运用微分方程建立鼠间鼠疫和人间鼠疫的传播动力学模型，用于描述鼠疫的流行特征，分析模型中各参数与疫情发展变化的关系[14-17]。

（2）利用统计数学模型研究鼠疫疫源地的自然因素（如气候、温度、降雨量等）与鼠类密度、媒介密度、鼠疫感染率等参数的相关性及其滞后特征[18-19]。

（3）从生态适应性、繁殖、生长发育、血液生化、冬眠和自带病原谱等方面研究疫鼠的生物学特性，建立鼠疫动物模型，从而为致病机理揭示、疫苗效果评价及鼠疫治疗方案选择提供依据[20-21]。

（4）筛选出与动物鼠疫流行相关性最大的监测指标，构建鼠疫疫源地鼠疫流行的预测预警模型，用于控制鼠疫的大规模爆发[22-23]。

在求解优化问题时，群智能优化算法采用的是启发式搜索策略，同时启动大量个体进行搜索。个体的行为以及个体之间的协同性变得十分重要。个体的行为可用算子来描述，个体之间的协同性就是群智能优化算法的逻辑结构。PIDO算法是基于具有脉冲预防接种的时滞鼠疫传染病模型[13]而构建的，其中个体的生物学含义就是某个生态系统中的人类个体，个体之间的协同性由鼠疫传染病的传播机制来体现，个体的行为由个体在易感、暴露、发病、治愈这4个状态之间的随机转换来体现。

PIDO算法采用与现有群智能算法不同的设计思路，提出了将脉冲预防接种的时滞鼠疫传染病模型转化为能求解一类大量局部最优解优化问题的方法，构造出的算子可以充分反映脉冲预防接种的时滞鼠疫传染病模型的相互作用关系，从而体现出鼠疫传染病动力学理论的基本思想，该算法具有全局收敛性。

2 鼠疫传染病优化算法设计方法

设要求解的优化问题为：

式中，Rn是n维欧氏空间，n为该优化问题所包含的实变量总数；X=(x1,x2,…,xn)是一个n维解向量；f(X)为目标函数，f(X)的数学表达式没有限制条件；H为搜索空间。

2.1 PIDO算法场景设计

假设在一个村庄Z中生活有N个村民，每个村民用编号表示为1,2,…,N；每个村民均由n个特征来表征，一个特征等价于村民的某个器官，即对第i个村民来说，其用特征表示为(xi,1,xi,2,…,xi,n)，i=1～N；该村庄Z中流行鼠疫，村民通过与带鼠疫病毒的老鼠进行有效接触，如被老鼠咬、吃老鼠肉或误食被老鼠粪便污染的食物，就会传染上鼠疫，鼠疫会在村民中传播；鼠疫病毒攻击的是村民的某些器官；该村庄中未染上鼠疫的村民称为易感者，他们染上鼠疫后，不会立即发病，其体内的病毒进入潜伏期；体内鼠疫病毒处于潜伏期的村民称为暴露者，他们也会将病毒传给与其有效接触的其他村民；潜伏期过后的暴露者会发病，这些村民称为发病者，他们更会将其体内的病毒传给与其有效接触的其他村民；发病者和暴露者可通过医学治疗被治愈；发病者和暴露者被治愈后称为治愈者；为了防止鼠疫病毒对村民们的危害，村民每隔一段时间接种一次疫苗，接种后的村民不会100%地成功获得免疫；成功获得免疫的村民在一段时间内自身不会染上鼠疫病毒；没有成功获得免疫的村民仍然是易感者；成功获得免疫的村民的免疫力在一段时间后会自动消失而丧失免疫力；没有实施免疫或丧失免疫力的村民会再次染上鼠疫病毒。在鼠疫病毒影响之下，该村庄中的每个村民的生长状态将在易感、暴露、发病、治愈这4个状态之间转换。这种转换映射到优化问题式（1）的H，相当于每个试探解在H中从一个位置跳转到另一个位置，于是达到了对H随机搜索的目的。每个村民的体质强壮程度由该村民的特征决定，体质强壮的村民能继续生长，体质虚弱的村民则停止生长。

把上述场景投射到对优化问题式（1）的全局最优解的搜索中，其含义如下：

优化问题的H与村庄Z相对应，该村庄中一个村民对应于优化问题式（1）的一个试探解，N个村民所对应的试探解集合就是X={X1,X2,…,XN}，Xi=(xi,1,xi,2…,xi,n)，i=1～N。村民i的一个特征j对应于试探解Xi的一个变量xi,j。因此，村民i与试探解Xi是等价的。村民的体质强弱用指数HHI（human health index，HHI）来表示，村民i的HHI指数按下式计算：

2.2 具有脉冲预防接种的时滞鼠疫传染病模型

为论述方便，把在一个村庄生活的村民分成4类：

（1）易感者（S 类）：即所有未染鼠疫的村民，若S类村民有效接触带鼠疫病毒的村民，就可能染上鼠疫。

（2）暴露者（E 类）：即已染上鼠疫病毒但还未发病的村民，他们是潜在发病者。

（3）发病者（I类）：即已染上鼠疫病毒且已发病的村民，I类村民有效接触S类村民，就可能把病毒传给S类村民。

（4）治愈者（R 类）：即E 类或I 类村民的治愈者，这群村民暂时尚不会得病，但经过一段时间后，若有效接触E类或I类病村民，还会重新染病。

具有脉冲预防接种的时滞鼠疫传染病模型[13]如式（3）所示。

式中，t为时期；R(t)、I(t)、E(t)、S(t)分别为时期t属于R类、I类、E类、S类人群的比例，R(t)≥0，I(t)≥0，E(t)≥0，S(t)≥0，R(t)+I(t)+E(t)+S(t)=1；其他参数如表1[13]所示。表中，Rand(A,B)表示在区间[A,B]产生一个均匀分布随机数；INT(w)表示将实数w按四舍五入取整。

Table 1 Meanings of parameters and method of taking value表1 参数含义与取值方法

时期t，因任意一个人只可处于R类、I类、E类、S类中的某个类，故R(t)、I(t)、E(t)、S(t)实际上是一个人属于R 类、I 类、E 类、S 类的概率；当一个人属于R类、I 类、E 类、S 类时，就表示一个人处于R 状态、I 状态、E状态或S状态。

因此，可以将式（3）应用于人群的任何一个人，即：

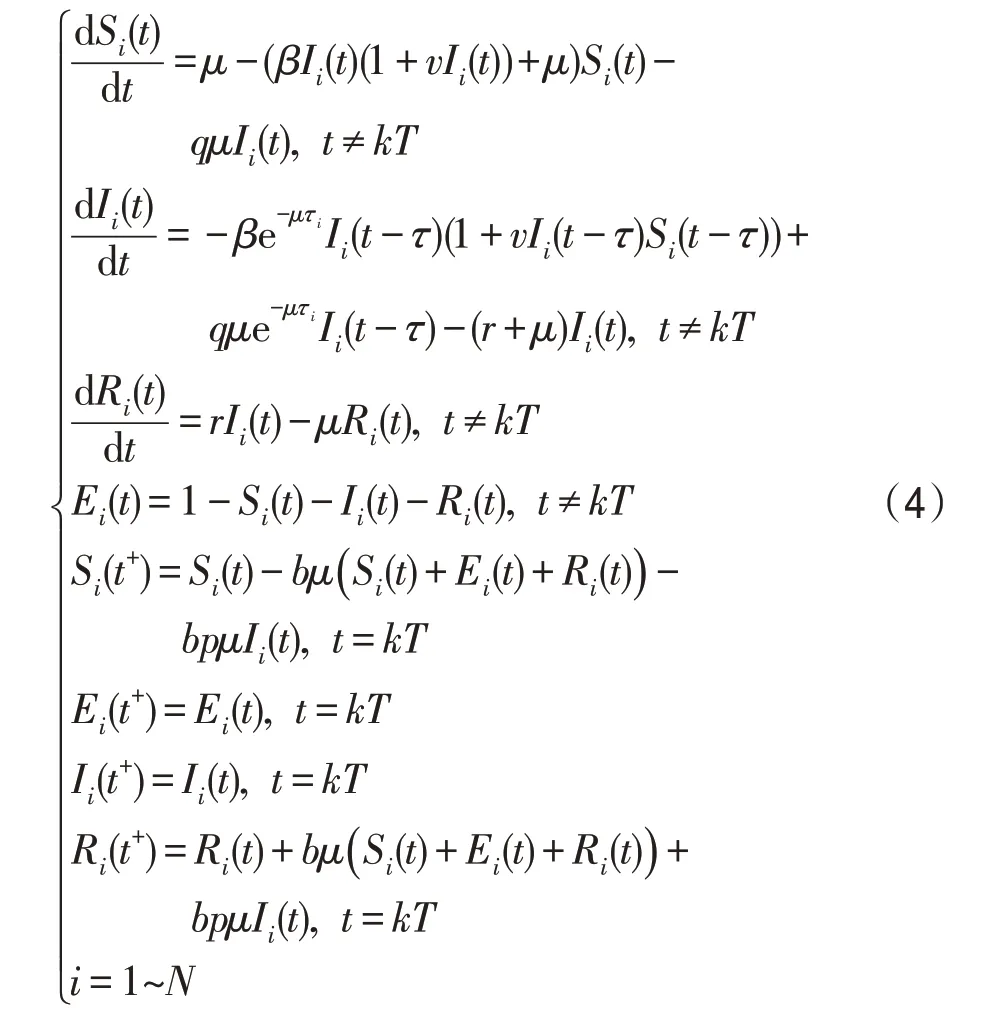
式（4）用于计算时期t每个人处于R状态、I状态、E状态和S状态的概率。

记时期t参数b、r、p、q、v、β、μ的取值分别为bt、rt、pt、qt、vt、βt、μt；为计算方便，将式（4）改为递推离散表达式，即：

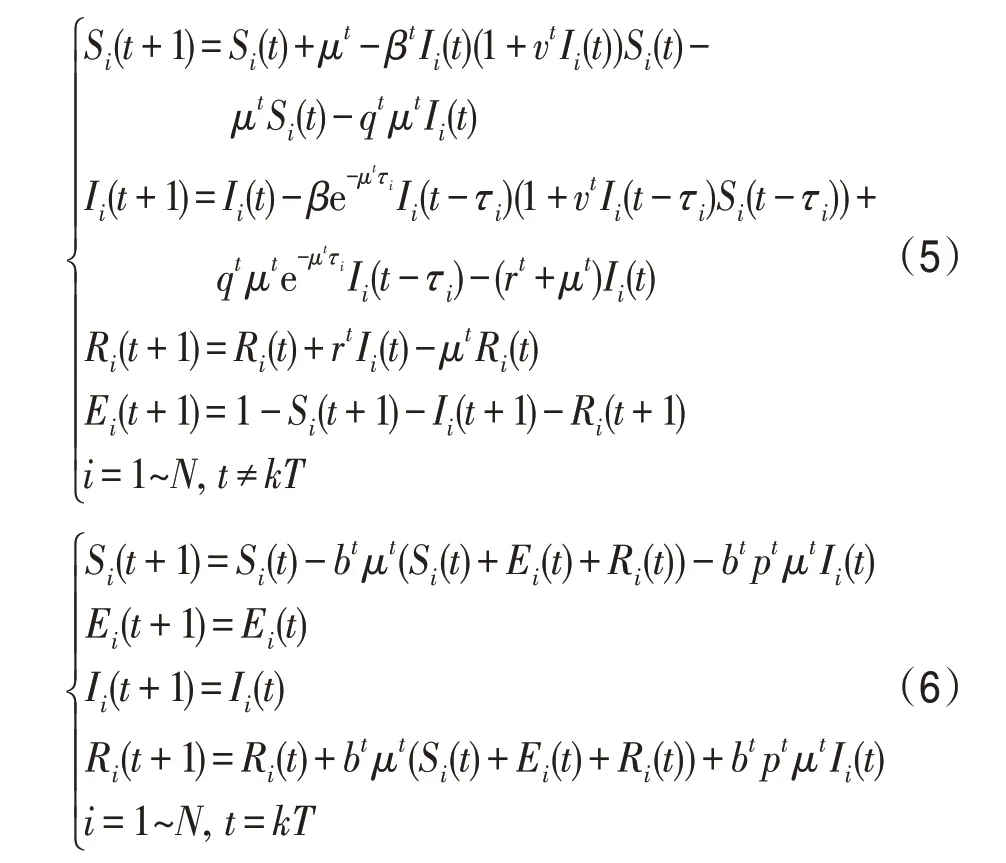
式（5）和式（6）中，Ri(t)、Ii(t)、Ei(t)、Si(t)分别为时期t个体i属于R 类、I 类、E 类、S 类人群的概率，Ri(t)≥0，Ii(t)≥0，Ei(t)≥0，Si(t)≥0，Ri(t)+Ii(t)+Ei(t)+Si(t)=1；参数bt、rt、pt、qt、vt、βt、μt，τi的取值方法如表1所示。

时期t，随机产生村民的bt、rt、pt、qt、vt、βt、μt、τi，采用式（5）和式（6）计算村民i的Ri(t)、Ii(t)、Ei(t)和Si(t)。村民i在时期t处于R 状态、I 状态、E 状态和S 状态4 个状态中的哪一个状态，由Ri(t)、Ii(t)、Ei(t)和Si(t)所构成的概率分布决定，即Ri(t)、Ii(t)、Ei(t)和Si(t)中的哪个值越大，其所对应的状态被选中的概率也越大。表2 给出了鼠疫病毒在村民中传播情形。

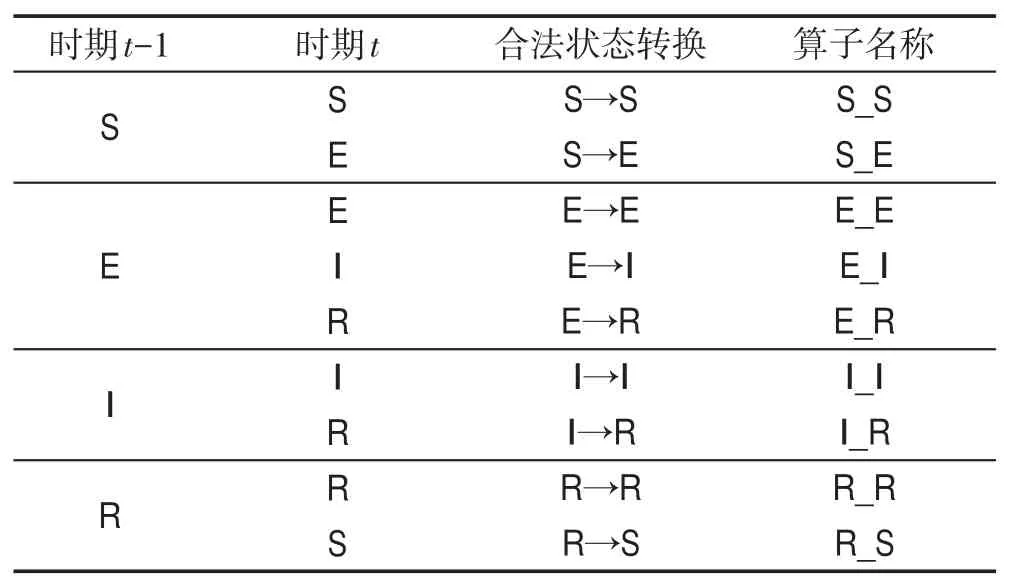
Table 2 Transformation of legal states of plague virus transmission表2 鼠疫病毒传播的合法状态转换

表2 所示的9 种合法状态转换可用图1 来表示，图中的每条弧对应一个算子。表2 所示的9 种合法状态转换可用9 个算子描述：S_S、S_E、E_E、E_I、E_R、I_I、I_R、R_R、R_S。

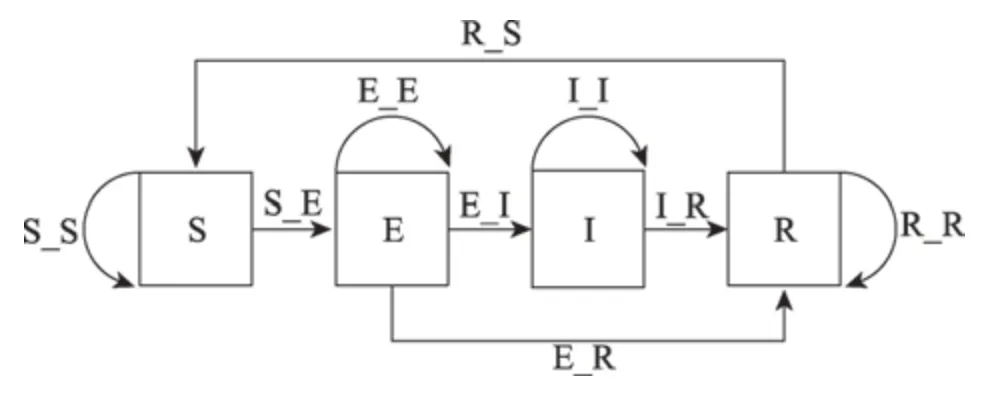
Fig.1 9 legal state transitions图1 9种合法状态转换

2.3 特征集合的生成方法

（1）优势村民集PSs的产生方法：从处于状态s的村民中随机选出L个村民，这些村民的HHI 指数比当前村民i高，组成优势村民集PSs，s∈{R,I,E,S}；L称为施加影响村民数。

（2）类别村民集CSs的产生方法：从处于状态s的村民中随机选出L个村民，组成类别村民集CSs，s∈{R,I,E,S}。

2.4 PIDO演化算子设计方法

（1）S_S算子。S_S算子描述的是：在时期t处于S 状态的村民，在时期t+1 仍未染上传染病的情形。对于处于易感状态S的村民i，有：

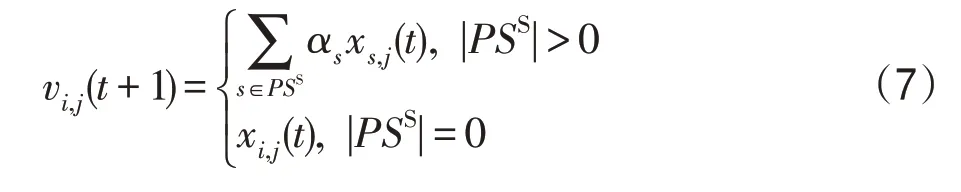
式中，vi,j(t+1)、xs,j(t)分别为时期t+1 和时期t村民i的特征j的状态值；αs为常数，αs=Rand(0.3,0.7)。

（2）S_E算子。S_E算子描述的是：在时期t处于S 状态的村民，在时期t+1 通过与已处于E 状态或I状态的村民有效接触后染上鼠疫病毒的情形。让L个已处于E状态或I状态的村民的随机选择的特征j的状态值经处理后传给处于S状态的村民i的对应特征j，使其染上鼠疫病毒，即成为暴露者。即对处于S状态的村民i来说，有：

（3）E_E算子。E_E算子描述的是：在时期t已处于E状态的村民，在时期t+1因潜伏期未满而还处于潜伏期的情形。让L个处于E 状态但其HHI 指数高于当前村民i的村民的特征j的状态值经处理后传给处于E状态的村民i的对应特征j，使其HHI指数提升。即处于E状态的村民i来说，有：

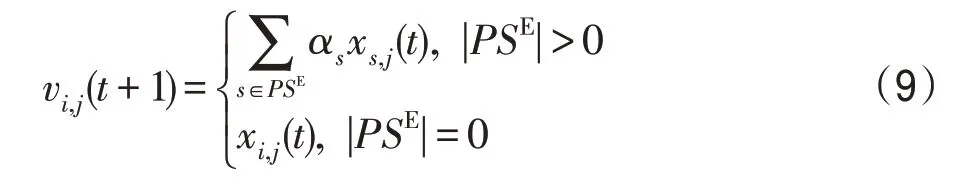
（4）E_I 算子。E_I 算子描述的是：在时期t已处于E状态的村民，在时期t+1因潜伏期已满鼠疫病毒开始发作的情形。L个处于I状态的村民的特征j的状态值经处理后传给已处于E 状态的村民i的对应特征j，使其发病。即对处于E状态的村民i来说，有：

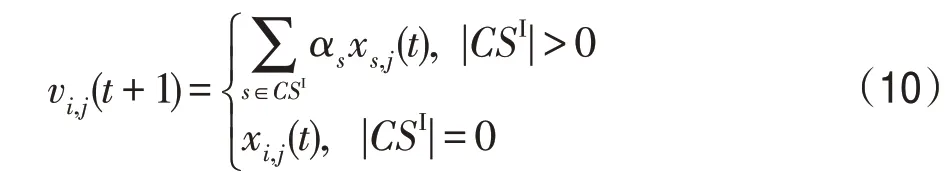
（5）E_R 算子。E_R 算子描述的是：在时期t已处于E状态的村民，在时期t+1通过治疗使其痊愈的情形。让L个处于R 状态的村民的特征j的状态值经处理后传给已处于E 状态的村民i的对应特征j，使其痊愈。即对处于E状态的村民i来说，有：

（6）I_I算子。I_I算子描述的是：在时期t已处于I状态的村民，在时期t+1 仍处于I状态的情形。让L个处于I状态但其HHI指数高于当前村民i的村民的特征j的状态值经处理后传给处于I状态的村民i的对应特征j，使其HHI指数升高。即对处于I状态的村民i来说，有：

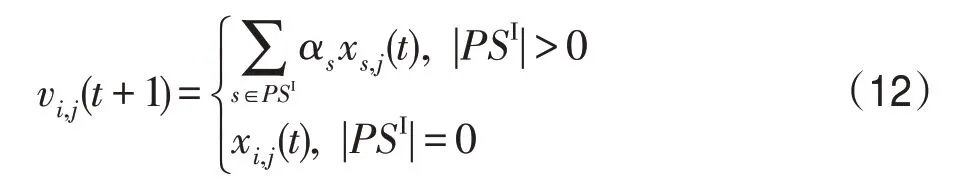
（7）I_R算子。I_R算子描述的是：在时期t处于I状态的村民，在时期t+1 通过治疗使其痊愈的情形。让L个处于R 状态的村民的特征j的状态值经处理后传给当前村民i的对应特征j，使其痊愈。即对处于I状态的村民i来说，有：

（8）R_R 算子。R_R 算子描述的是：在时期t已处于R 状态的村民，在时期t+1 仍处于R 状态的情形。让L个处于R状态但其HHI指数高于当前村民i的村民的特征j的状态值经处理后传给处于R 状态的村民i的对应特征j，使其HHI 指数升高。即对处于R状态的村民i来说，有：

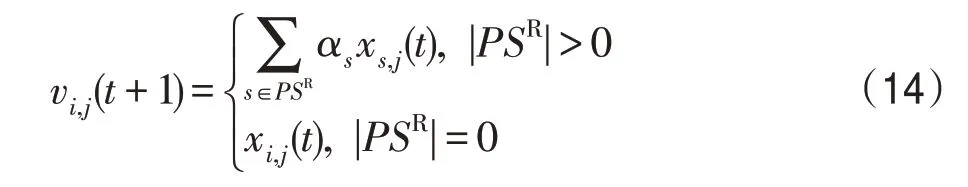
（9）R_S算子。R_S算子描述的是：在时期t处于R状态的村民，在时期t+1 因免疫力消失而转为S状态的情形。让L个处于S 状态的村民的特征j的状态值经处理后传给当前村民i的对应特征j，使其转为S状态。即对处于R状态的村民i来说，有：

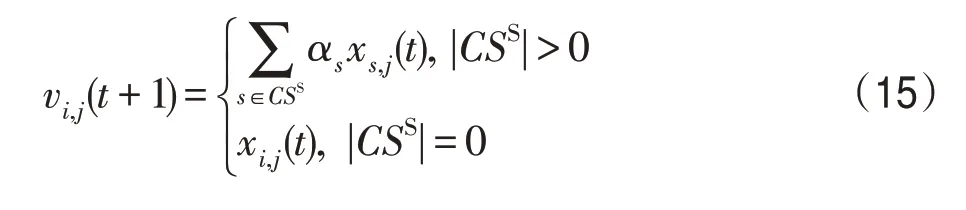
（10）生长算子。该算子描述的是村民的生长，即：

式中，Xi(t)=(xi,1(t),xi,2(t),…,xi,n(t))，Vi(t+1)=(vi,1(t+1),vi,2(t+1),…,vi,n(t+1))。HHI(Xi(t))、HHI(Vi(t+1))按式（2）进行计算。

2.5 PIDO算法的构造

步骤1初始化：（1）令t=0。演化时期数G=8 000～60 000，误差要求ε=10-5～10-10，N=50～500，村民接种疫苗成功的概率Q0=0.5～0.9，村民受影响概率E0=1/1 000～1/100，L=3～6，T=3～10。（2）在H中随机选择N个村民所对应的试探解[X1(0),X2(0),…,XN(0)]。（3）令V(i)=0，i=1～N。V(i)=0 表示村民i疫苗接种未成功或未接种；V(i)>0 表示村民i疫苗接种成功。（4）随机选择全局最优解Y*初始值。

步骤2Ii(0)，i=1～N。

步骤3计算村民i的RIES状态，RIESi(0)=RIES(Si(0),Ei(0),Ii(0),Ri(0))，i=1～N。其中RIESi(0)为时期0 村民i所处的状态；函数RIES(Si(0),Ei(0),Ii(0),Ri(0))用于确定村民i将处于哪种状态。

步骤4结束。

函数RIES(pS，pE，pI，pR)的定义如下：

2.6 PIDO算法的特点

（1）时间复杂度。PIDO 算法的时间复杂度计算过程如表3所示。

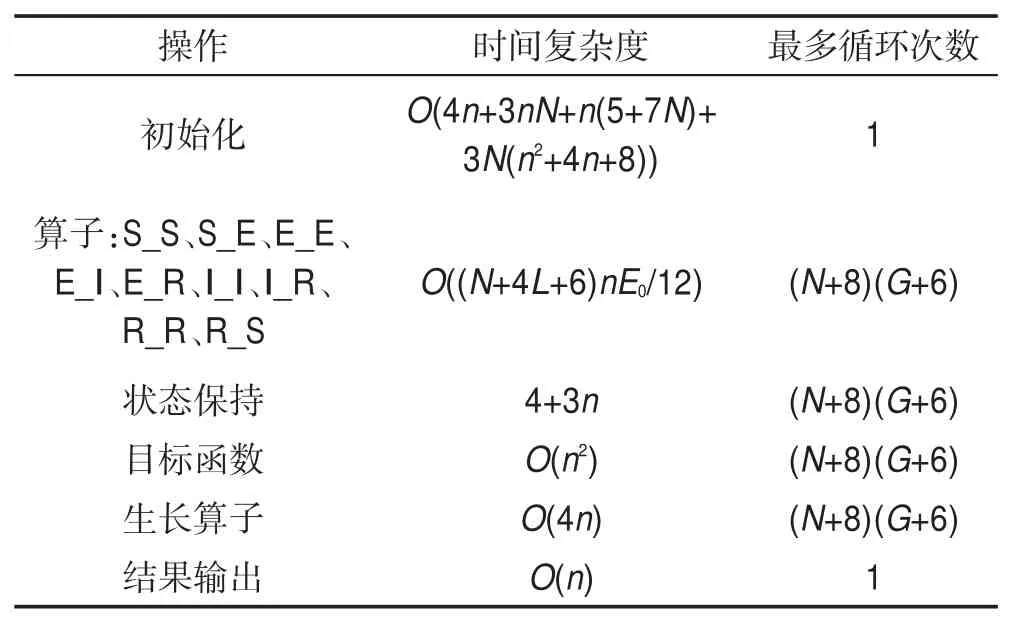
Table 3 Time complexity table for PIDO algorithm表3 PIDO算法的时间复杂度计算表

（2）Markov 特性。从S_S、S_E、E_E、E_I、E_R、I_I、I_R、R_R、R_S等算子的定义的式（7）～式（15）知，任意一个在时期t+1 的新试探解X(t+1)的计算生成只与其在时期t的状态X(t)有关，而与其以前是如何演变到当前状态的历程无关，表明PIDO算法的演进过程具有Markov特性。

（3）从生长算子的定义式（16）知，时期t+1 任一村民的HHI 指数永远不会低于其在时期t时的HHI指数，表明PIDO 算法的演进过程具有“步步不差”特性。

3 PIDO算法全局收敛性证明

由PIDO算法知，村庄Z与搜索空间H等价，将村庄内的N个村民{X1(t),X2(t),…,XN(t)}排列成序列村民数为N，一个村民等价于一个试探解，其目标函数值为，所有村民的状态所形成的集合为：

进一步令：

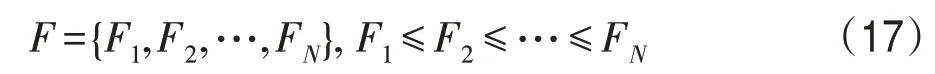
不失一般性，令F1即为所求的全局最优解。由式（17）的下标可得集合：

U={1,2,…,N}

∀i∈U，i就是村民i执行随机搜索时可能处的状态。假设在时期t村民i搜索到的最好目标函数值为Fi，其对应的状态为i。显然，由式（17）知，在时期t+1村民i进行搜索时，若向更优的状态k转移，则应满足ki，如图2所示。

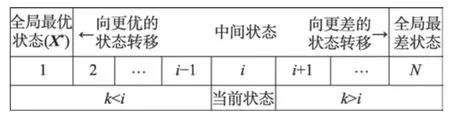
Fig.2 State transition of PIDO algorithm in random search图2 PIDO算法随机搜索时的状态转移

∀X∈H，有F1≤F(X)≤FN，将H划分成子集：

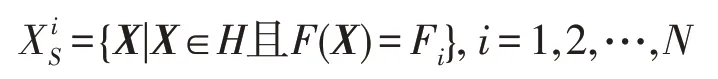
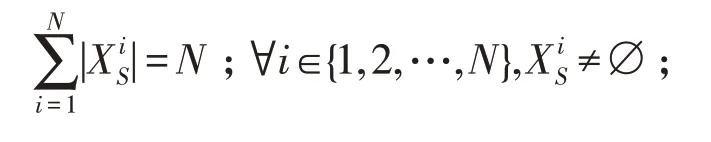
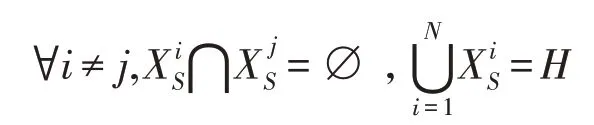
引理1在PIDO 算法中，i=1,2,…,，满足：

（1）引理式（19）的证明：设状态i为时期t村民i的状态，其在H中对应的位置为Xt，由2.6 节知，PIDO算法的随机搜索过程具有步步不差的特性。故在时期t+1，村民i不会转移到任何更差的状态上去，如图2所示，故有：

（2）引理式（20）的证明：设状态i为时期t村民i的状态，在时期t+1，村民i随机选择S_S、S_E、E_E、E_I、E_R、I_I、I_R、R_R、R_S 等算子进行演化以便转移到更好的状态k上。此时，存在有如下两种情况：

①若状态i就是全局最优状态，也即i=1，则下一步转移仍留在原状态，即k=i=1，这是因为由2.6节知，村民i不会转移到比原状态i更差的其他状态上去，故必以概率p1,1=1 留在原状态i上。因p1,1=1>0，命题得证。

②若状态i不是全局最优状态，则在状态1和当前状态i之间必至少存在一个中间状态k，如图2 所示，使得F1≤Fk0。命题得证。

综上所述，可得∃k0。 □

定理1[24]设P′是一n阶可归约随机矩阵，即通过相同的行和列变换后可得到，其中C是m阶本原随机矩阵，且T≠0，R≠0，则有：

上述矩阵是一个稳定随机矩阵，P′∞=1′P′∞，P′∞=P′0P′∞唯一确定且与初始分布无关，P′∞满足条件：

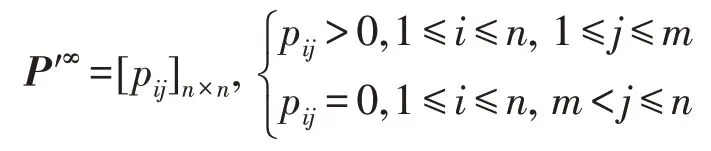
定理1的证明过程可参见文献[24]。

定理2PIDO算法具有全局收敛性。

证明由2.6 节知，PIDO 算法的搜索过程具有Markov 特性。对于每个,i=1,2,…,2N可看作是有限Markov 链上的一个状态，根据引理中式（19）的结论可得该Markov链的状态转移矩阵为：

由式（18）知，P′中每行的概率之和等于1。又根据引理中式（20）的结论可得：

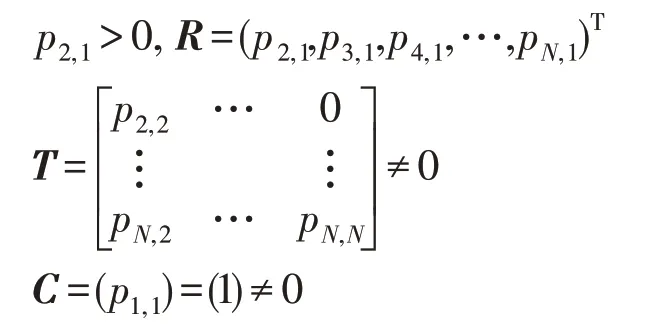
由以上可知，P′是一个N阶可归约随机矩阵，即Markov状态转移矩阵，满足定理1的条件，故有：

因C∞=C=(1)，T∞=0，故必有R∞=(1,1,…,1)T，这是因为P′中任意一行的概率之和总为1，故有：

上式表明，当k→∞时，pi,1=1，i=1,2,…,N，即无论各村民初始状态如何，最后都能以概率1转移到全局最优状态1上去。于是有：

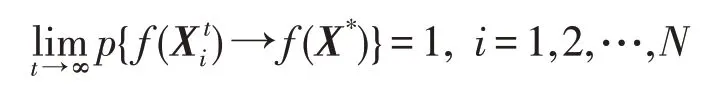
因此，PIDO算法具有全局收敛性。 □

4 PIDO算法性能分析

4.1 村民数量对PIDO算法性能的影响分析

下面以著名的Bump 优化问题和Michalewicz 优化问题为例对PIDO 算法在不同村民数量设置下的性能进行分析，这两个优化问题求解难度很大。

Bump优化问题：

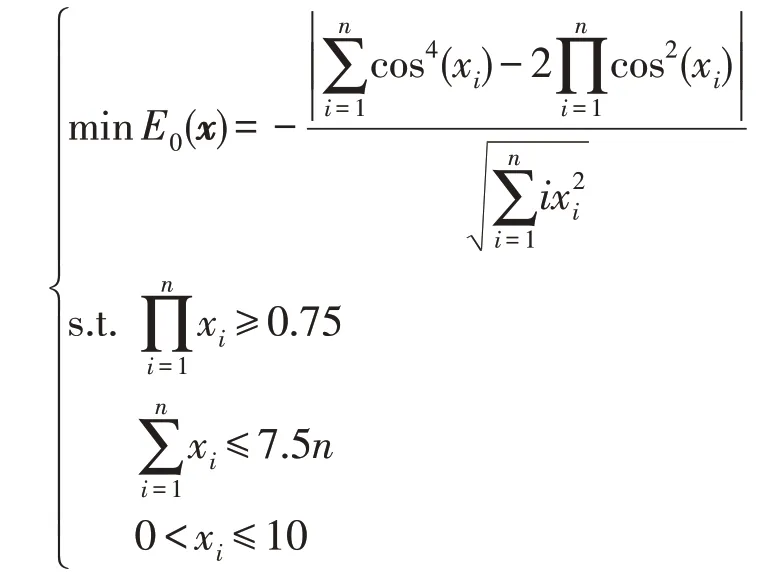
Michalewicz优化问题：

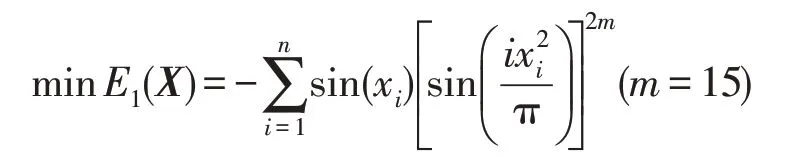
利用PIDO 算法求解Bump 优化问题和Michalewicz 优化问题，计算结果如表4 所示。计算时，G=107，ε=10-7，Q0=0.9，L=3，T=3。

从表4可以看到：

（1）当N增加时，消耗的CPU时间大大增加。

（2）对于给定的n，如果N增加，CPU消耗时间也大大增加，但平均最佳目标函数值的精度同时增加。

（3）对于给定的n和N，如果E0增加，平均最佳目标函数值的精度也增加，但是消耗的CPU 时间可能增加或减少。

因此，如果n＞500，N=100～200 就足够了；如果n＜500，N=200就足够了。

Table 4 Comparisons of calculation results under different parameter settings表4 不同参数设置下的计算结果对比

4.2 与其他群智能算法的比较

本文采用国际上通用的智能优化算法测试包CEC2013[25]所提供的6 个基准函数优化问题来测试PIDO 算法的性能，如表5 所示。该测试包括有28 个经过精心设计的基准函数优化问题。

表5 中O是可以任意设定的理论全局最优解。F14、F25、F28的理论全局最优解目前尚未发现，表5中的全局最优目标函数值是本文算法发现的迄今为止最好的目标函数值。本文用PIDO算法求解表5中的6 个函数优化问题，其参数是N=200，n=50，G=107，ε=10-7，Q0=0.9，E0=0.01，L=3，T=3。与PIDO算法进行比较的7种智能优化算法均选自国际著名期刊近期刊登的算法，这些算法如表6 所示，即RCGA（real-coded genetic algorithm）、DASA（differential ant-stigmergy algorithm）、NP-PSO（non-parametric particle swarm optimization）、MpBBO（metropolis biogeography-based optimization）、MDE-LiGO（modifieddifferential evolution with locality induced genetic operators）、SLADE（symmetric Latin-based adaptive differential evolution）、ABC（artificial bee colony algorithm）。这7 种算法的终止运行条件为：进化代数G=107或者最优解误差ε=10-7。

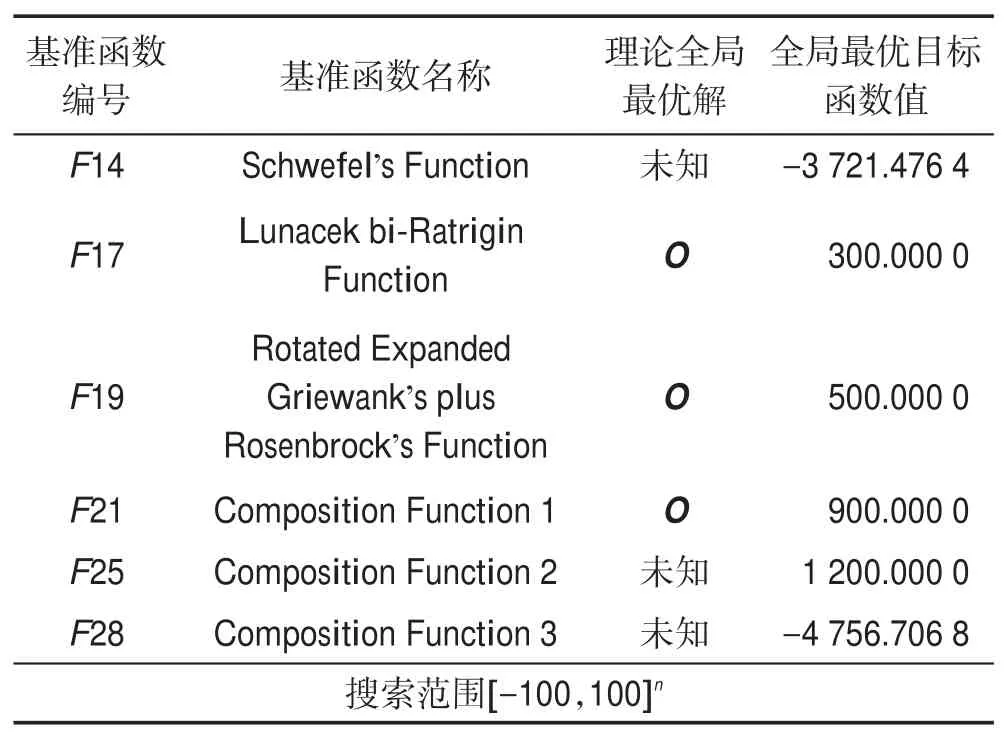
Table 5 6 benchmark function optimization problems表5 6个基准函数优化问题

Table 6 Parameters setting of compared intelligent optimization algorithms表6 参与比较的智能优化算法的参数设置

表6中各参数的含义可参见相关文献。针对表5中列出的6个优化问题，用PIDO算法和表6列出的7种算法进行求解，每种算法均独立求解51 次。表7给出了8种算法所求得的最优目标函数值的平均值、标准差、中值、最小值、最大值、适应度评价次数。

总排名1 是这些算法基于平均最优目标函数值进行的排名，总排名2是这些算法基于平均最优目标函数值和适应度评价次数进行的排名；最终总排名1和最终总排名2分别是基于总排名1和总排名2所进行的排名。

非参数Friedman检验[26-27]是基于PIDO算法所得的结果与7 种被比较算法所获得的结果之间进行的非参数检验。Friedman检验的结果显示在表8中，其中显著性＝1表示PIDO算法的性能与被比较算法具有99%的统计学差异，显著性＝0 表示没有显著差异。在表8 中，显著性＝1 的案例数和显著性＝0 的案例数分别表示PIDO算法与7种被比较算法显著不同和没有显著差异地求解基准函数优化问题的数目。

从表7 可以看出PIDO、RCGA、DASA、NP-PSO、MpBBO、MDE-LiGO、SLADE、ABC按平均最优目标函数值的精度进行排序所得的结果如下：

按平均最优目标函数值和适应度评价次数进行排序所得的结果如下：

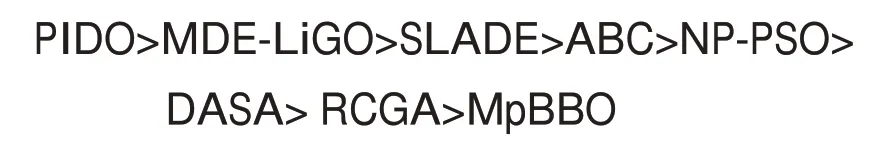
从表8可以知道，PIDO算法求解6个基准函数优化问题的显著性案例总数为39，明显大于不显著性案例总数3，表明PIDO算法的性能明显优于7种被比较算法。

图3（a）～图3（f）说明PIDO、RCGA、DASA、NPPSO、MpBBO、MDE-LiGO、SLADE、ABC 算法求解表5 所示的6 个基准函数优化问题时的样本收敛曲线，其中水平和垂直轴采用对数刻度。从图3 和表7均可以看出，当PIDO 算法求解6 个基准函数优化问题时，均能发现质量最好的全局最优解。综合看来，PIDO 算法的综合性能要优于7 种被比较算法，表明其求解精度高且计算速度快。

4.3 局部寻优能力和全局寻优能力分析

本文采用文献[28]提出的方法来对PIDO算法的局部和全局寻优能力的平衡性进行分析。其中穿透行为用来说明PIDO算法的全局寻优能力，而膨胀行为用来说明PIDO算法的局部寻优能力。

图4显示了当PIDO算法求解基准优化问题F3[25]时，穿透和膨胀行为在时间间隔[0，694]和[0，966]内的协调关系。从图4 可以看出，穿透行为在0 s 到120 s占优，而膨胀行为在之后120 s占优。

Table 7 Optimal solutions obtained by 8 compared algorithms表7 8种参与比较的算法所获得的最优解

续表7

Table 8 Results comparison of Friedman test(α=0.01)表8 Friedman检验结果比较(α=0.01)

图5分别说明了当PIDO算法求解F3时，在时间间隔[0，694]和[0，966]内膨胀和粘滞行为之间的协调性。从图5 中可以看出，膨胀行为总是占优，粘滞行为根本不占优，但是膨胀行为的占优随着时间的流逝而减少；相反，粘滞行为出现的次数随时间而增加。

5 结束语

PIDO具有如下特点：

（1）PIDO算法包括S_S、S_E、E_E、E_I、E_R、I_I、I_R、R_R、R_S等9个算子，这些算子可明显地增加该算法的搜索能力。

（2）采用随机方法确定PIDO算法中的鼠疫传染病模型中的参数和各算子中的相关参数，既可使模型更能表达实际情况，又大幅减少了输入的参数个数。

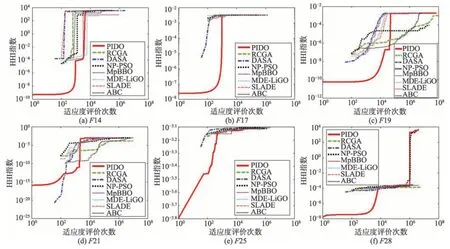
Fig.3 Convergence curves of samples图3 样本收敛曲线

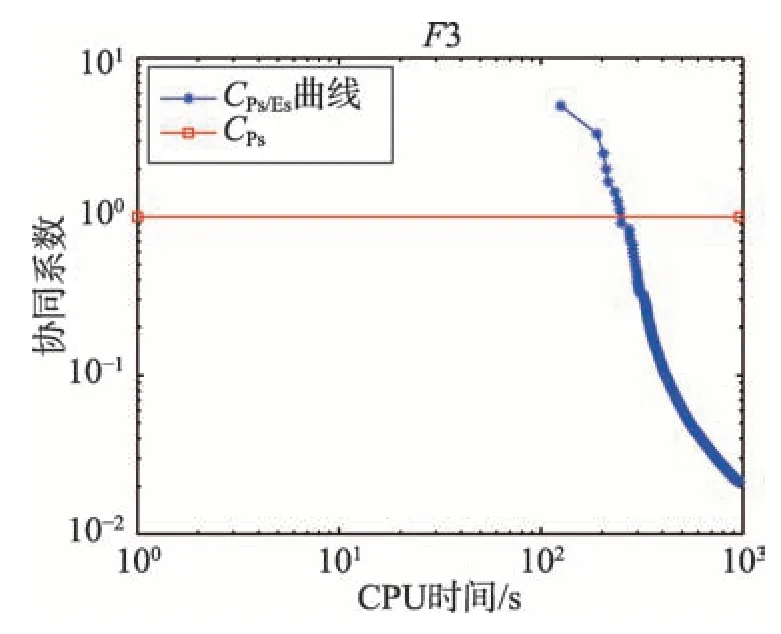
Fig.4 Coordination of penetration and expansion behavior图4 穿透行为和膨胀行为之间的协调性分析

（3）PIDO 算法中的算子S_S、S_E、E_E、E_I、E_R、I_I、I_R、R_R、R_S是利用鼠疫传染病模型来构造的，不需要与求解的问题相关，因此PIDO 算法具有通用性。

Fig.5 Coordination of expansion and stickiness behavior图5 膨胀行为和粘滞行为之间的协调性分析

（4）在PIDO算法中，算子S_S、E_E、I_I和R_R能使HHI指数高的村民向HHI指数低的村民传递强壮特征信息，从而使后者能向好的方向发展；算子S_E、E_I、E_R、I_R 和R_S 既能使处于不同状态的村民之间交换信息，又能使村民获得其他村民经处理后的特征信息，降低了村民落入局部最优陷阱的几率，从而提升了PIDO 算法的局部求精(exploitation)能力；脉冲式预防接种拥有使村民跃出局部最优陷阱的特性。因此，PIDO 算法能从多个角度实现村民之间的信息交换，这对提升PIDO算法的搜寻(exploration)能力有意义。

（5）在PIDO 算法进行演化计算时，由于只有村民的极少部分特征被鼠疫病毒攻击，因此每次村民之间交换信息，只有极少部分特征参与计算，从而当求解维数较高的优化问题时，PIDO 算法收敛速度可显著提升，PIDO算法适于求解维数较高的优化问题。

（6）PIDO 算法的演化过程具有Markov 特性和“步步不差”特性，从而确保该算法具有全局收敛性。

PIDO算法未来的改进方向如下：

（1）利用鼠疫传染病动力学模型优化PIDO算法的相关参数，使得这些参数设置更合理。

（2）深入研究S_S、S_E、E_E、E_I、E_R、I_I、I_R、R_R、R_S等算子的动态特征。

（3）深入研究PIDO算法求解过程中村民们的动态特征。