一种基于K-近邻分区的蚁群算法在TSP问题中的应用研究

◆黄泽斌 黄钢忠 杨志鹄 姜春涛 黄颖欣

（佛山科学技术学院数学与大数据学院 广东 528000）

旅行商（TSP）问题是一种组合优化问题，指的是旅行者从一个城市出发，经过剩余城市，且每只经过一次，最后返回出发城市的最短旅程[1]。如今，国内外很多学者从很多不同算法入手来研究此问题，并取得了不错的成果，如：粒子群算法、蚁群算法、遗传算法等。

其中，蚁群算法是一种模拟蚂蚁群体一起觅食行为的智能算法。该算法于1992年，由米兰理学院学者M.Dorigo首次提出，它具有良好的鲁棒性、支持分布式的计算和能够进行全局搜索的优点，并被广泛应用在求解TSP问题、job-shop分配问题、蛋白质折叠问题等许多与组合优化相关的问题，而且能够得到良好的结果。本文在此算法基础上，将K-近邻的思想与其相结合，编写新的蚁群算法程序，并通过在TSP问题中的应用来验证新算法的可行性。

1 基本原理

1.1 蚁群算法基本原理

蚁群算法是用于搜索和优化路径的模拟进化算法。蚁群在觅食过程中，每只蚂蚁都会留下一种用于信息传递yon的物质，我们称之为信息素。研究表示，信息素浓度愈高，蚂蚁的选择意向便会愈强，众多的蚂蚁组成的群体行为形成一种协同搜索最优路径的正反馈机制：某条路径的信息素浓度愈高，便表明该路径更短，而随着时间的流逝，路径上的信息素又会一直进行自我衰减[2][3]。最后，基于这种正反馈机制，蚁群可以找到食物和巢穴之间的最短路径。其过程如图所示。

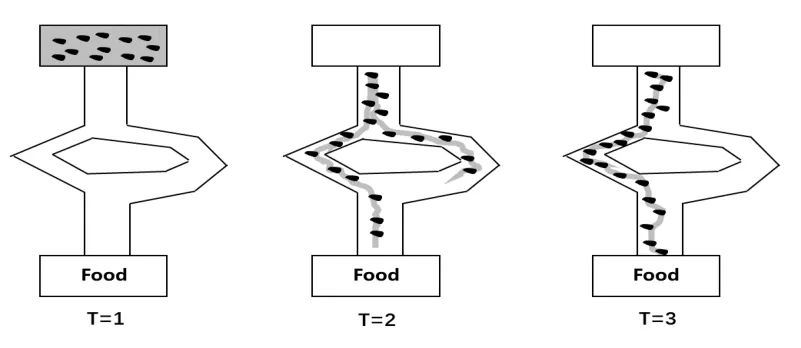
图1 蚁群算法原理图

在图1中，当T=1时，图为蚁群搜寻食物的初始图，假设仅有图中左右两条路径可以到达食物源Food，从图中也可以明显看出，左边的路径长度远小于右边的路径长度；

在图1中，当T=2时，图为蚁群搜寻食物的过程图，在图中有左右两条路径到达食物源Food，所以，两条路线均有蚂蚁爬行；

在图1中，当T=3时，图为蚁群寻找到食物源最优路线的生成图，在此过程中，沿路的信息素浓度由于有了多数的蚂蚁通过而升高，路径的信息素浓度愈高，则说明此路径愈短，而在蚁群中信息正反馈机制的基础上，能够让所有的个体蚂蚁都选择信息素最高的路径即是最短路径。

1.2 蚁群算法模型

假设在m个城市之间的路径有n只蚂蚁上移动，不同的蚂蚁借助信息素达到在运动时的交流目的，以此来决定下一步移动的方向，通过公式（1），可以算出在城市j中的蚂蚁k选择移动到下一个城市i的概率，其概率公式为：

使用禁忌表tabuk记录蚂蚁k已留下信息素的城市，确保蚂蚁不会再选择这些城市。当禁忌表记录了所有城市节点时，说明蚂蚁k成功完成了一次对所有目标城市的循环，此时便可得到一个旅行商的可行解，与此同时更新所有路径上现有的信息素。信息素更新的公式如：

在蚁密系统模型中：

在蚁量系统模型中：

在蚁周系统模型中：

式中，Q作为信息素的强度；Lk是第k只蚂蚁走过完整一条路径后所得到的路径全长。在以上3个模型中，蚁密模型和蚁量模型的原理都是通过考虑蚂蚁经过路径的局部信息来对信息素浓度进行更新；而蚁周模型是在蚂蚁运动过程中的整体信息的基础上更新信息素的浓度。所以，对于旅行商问题，蚁周模型因具有更好的优越性而被广泛采纳。

1.3 K-近邻分区方法

K-近邻算法是一种监督学习分类算法，属于回归和分类方法中的一种。通过K-近邻算法来进行分区操作，可以提高蚁群算法在TSP中路径规划的效率。假设一个TSP路径优化问题有n个节点，用N1,N2,...,Nn表示，同时为k-近邻算法设定一个分类距离阈值D，然后按照以下步骤进行分区操作：

（1）从所有节点中，随机为第一子区域的中心选取一节点NC，且令，然后计算所有剩余节点NC到K1的距离d1c，将d1c与分类距离阈值D进行比较，若，则可将Nj归属到第一子区域节点中；若，则将Nj作为到第二子区域中心K2；

（2）若有Nk到K1,K2的距离d1k,d2k都大于D，则将Nk选为一个新的子区域中心，接着计算剩下所有节点Nj到已有子区域Nk的距离djk，若，则将节点Nj分类到与它距离最小的子区域中，否则，将一个新子区域中心设定为Nj。

1.4 K-近邻分区蚁群算法求解TSP问题的步骤

（1）以横、纵坐标方式表示待求解TSP问题中的所有节点数据；

（2）用K-近邻分区方法对所有节点数据进行聚类分区；

（3）对每个子区域用蚁群算法进行最优化求解；

（4）连接子区域之间距离最近的点，并输出问题的最终解。

2 实验方法及实验结果

为了解决传统的蚁群算法在求解TSP问题时，遇到巨大优化性能和时间消耗的问题，本文在此算法的基础上，加入K-近邻分区算法，实现在TSP问题求解时，先分区再求解的操作，并对此进行实验仿真。

实验中，进行TSP问题仿真求解时，分别选取了60，120个节点。首先，利用K-近邻算法对所有节点进行分区，接着利用蚁群算法对每个子区域进行最优化求解，最后，连接这些子区域之间距离最近的点。

图1是对60个节点进行优化求解之后的路径示意图，最终的路径长度是332.8252，图2是对120个节点进行优化求解之后的路径示意图，最终的路径长度是433.2763。

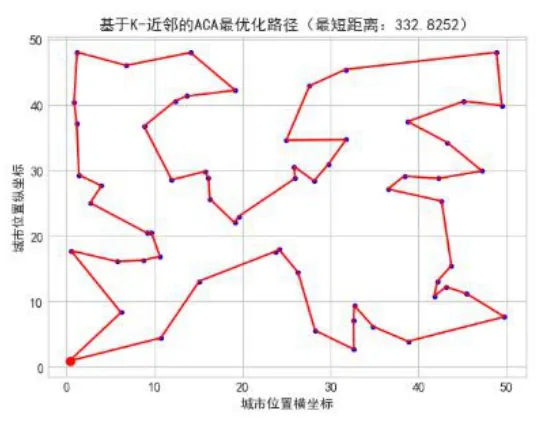
图2 60个节点的局部优化路径图

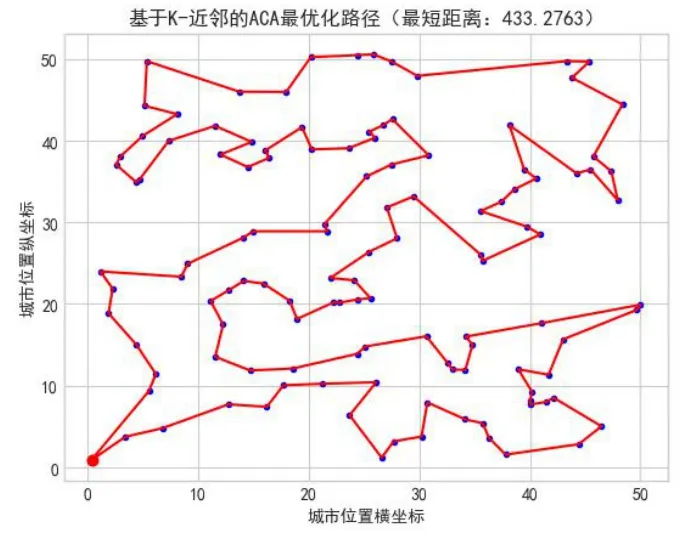
图3 120个节点的局部优化路径图

3 结束语

通过对基本蚁群算法和K-近邻分区方法在TSP问题中的应用研究，提出了一种基于K-近邻分区的蚁群算法。主要目的是解决蚁群算法在优化性能和时间性能上的巨大消耗。实验结果表明，在解决小规模TSP问题时，该方法所得的结果较好，但当节点增多到120个时，所得结果会相对于全局优化的结果差。而在平时进行TSP大规模求解时，倘若运行设备不能满足大规模运算，则需要进行分区求解，所以此方法还是比较适用的。