基于微地震数据和嵌入式离散裂缝的页岩气开发渗流数值模拟

戴 城，胡小虎，方思冬，郭艳东

（中国石化石油勘探开发研究院，北京100083）

1 研究背景

随着天然气需求量的增加，页岩气作为一种重要的非常规天然气资源日益受到世界各国的关注。包括中国在内的众多国家正积极采取相应措施，努力推进页岩气的商业化开采。截至2015年4月，我国页岩气勘探在长宁、威远、昭通、涪陵等地取得突破，获得三级储量近5 000×108m3，已形成年产15×108m3产能[1]。

在此背景下，围绕页岩气勘探开发方面的探索也得到了国内外学术界、工业界的广泛重视。页岩气藏与常规天然气藏不同，具有自生自储特征，生烃层即为储层[2]。页岩气在储层中通常以吸附态和游离态两种形式存在。与常规天然气藏相比，页岩气藏储层孔隙度、渗透率极低，孔隙度通常小于10%，渗透率介于10-11～10-7μm2[3]。正是由于页岩气藏的低渗特性，在页岩气开发过程中，需要采用分段压裂水平井技术对页岩储层进行压裂改造以提高产量。水力压裂会构建复杂裂缝网络，在储层中形成一个渗透率相对较高的压裂改造区域。在压裂改造区外围，储层未经改造，天然裂缝没有被人工裂缝沟通，渗透率相对较低。

数值模拟技术是研究油气藏开发机理的重要工具。针对页岩气开发，国内外诸多研究者利用数值模拟进行了研究。CIPOLLA等[4-5]研究了单井产能的影响因素，发现裂缝网络复杂程度、主裂缝导流能力、基质渗透率等会对单井产量造成影响。双重介质模型[6-7]和多重介质模型[8-10]是页岩气数值模拟经常采用的数值模型。YANG等[11]采用双孔双渗模型，动态分析了Antrim页岩和Barnet页岩产量中吸附气和自由气的比例。页岩不同孔隙中流动遵循不同的流动规律[12]，WU等[13]在页岩气数值模拟过程中考虑了页岩气藏低渗储层内的Knudsen扩散、气体滑脱效应对产量的影响。采用双重介质模型和多重介质模型的数值模拟方法对整个裂缝网络进行了等效简化，无法准确刻画压后裂缝网络各条裂缝的走向、开度等关键信息，因此，无法准确模拟分层的储量动用情况。糜利栋等[14]基于非结构化网格系统采用离散裂缝网络模型及有限元方法对压后页岩气藏进行模拟，定量分析了裂缝网络的发育程度对产能的影响。离散裂缝渗流模拟方法基于非结构化网格，以裂缝面为约束，在裂缝面附近剖分非结构化网格，计算相应传导率，继而进行模拟。离散裂缝渗流模拟的出现提高了裂缝性油气藏模拟的精度，但是该方法也依然具有非结构化网格剖分困难、计算量巨大等缺点。

近年来，国际研究者结合等效介质模型和离散裂缝模型的思路逐步发展了一套新的嵌入式离散裂缝模拟体系。以结构化网格为背景网格，将裂缝嵌入背景网格中，以非相邻连接将二者相连。严侠等[15]研究发现嵌入式离散裂缝渗流模拟可以在不损失精度条件下提高计算效率。YAN等[16]、卫云鹏等[17]将嵌入式离散裂缝与双孔模型相结合用于页岩气模拟，以双孔模型表征天然微裂缝网络，以嵌入式离散裂缝表征大尺度水力裂缝。但以上研究均只针对二维或拟三维算例，对于三维算例的研究还未开展。

为了更加快速准确描述压后改造缝网，在调研国内外嵌入式离散裂缝研究基础上，自主研发了基于嵌入式离散裂缝的三维页岩气渗流数值模拟方法，采用嵌入式离散裂缝精确刻画储层内每一条压裂裂缝形态，继而通过基质裂缝间的非相邻连接模拟储层流动。与传统等效介质模型相比，嵌入式离散裂缝无需对裂缝进行任何等效操作，可以精确地刻画压后缝网内每一条裂缝的分布、走向及开度信息。因此，基于嵌入式离散裂缝模型的模拟结果较传统等效介质模型更为精确。与离散裂缝模型相比，嵌入式离散裂缝的储层无需进行非结构化网格剖分，避免了非结构化网格剖分造成的数值不收敛问题，极大地提升了计算效率。对于页岩气开发渗流数值模拟工作而言，该方法可以在常规地质建模软件输出的压前模型中便捷地嵌入裂缝，提升了模拟工作的效率。

2 研究方法

嵌入式离散页岩气渗流数值模拟方法其基本思路是将裂缝视为矩形裂缝片嵌入至结构化的储层网格中，嵌入至储层网格中之后，裂缝片将被储层网格切割为不规则的裂缝网格，组成一套非结构化网格系统。通过计算裂缝网格和相邻裂缝网格，裂缝网格和储层网格之间的传导率可以构建数值模拟连接表，遍历连接表即可进行数值模拟运算。该方法适用于分段压裂水平井开发的页岩气藏，精确刻画压后缝网分布。基于以上基本思路，本课题组采用C++自主研发了基于嵌入式离散裂缝页岩气渗流数值模拟器。模拟器的具体细节及其与商业模拟器的对比见文献[18]，这里只针对嵌入式离散裂缝构建问题展开讨论。采用嵌入式离散裂缝模型模拟的关键环节是传导率的计算，就关键环节展开讨论。所有公式均采用国际单位制。

2.1 页岩气藏渗流控制方程

在描述页岩气藏时，将整个气藏划分为两大部分，即基质和裂缝。然后对基质和裂缝中的流动分别建立数学模型。建立控制方程的思路是保证一定时间内控制体内质量守恒，即流入量等于流出量加上源汇项。

在基质中，组分c的守恒方程为：

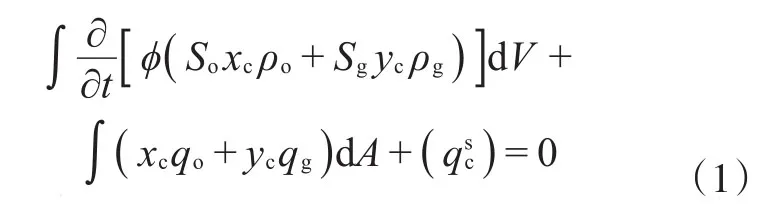
式中：V为控制体积，m3；A为控制体表面积，m2；φ为孔隙度，%；So和Sg分别为油饱和度和气饱和度，%；ρO和ρg分别为油相摩尔密度和气相摩尔密度，mol/m3；xc和yc分别为组分c在油相和气相的摩尔分数，%；qo和qg分别为油相和气相的摩尔流速，kmol/（m2·s）；qsc为基质解吸附的组分c扩散进入基质网格的摩尔速率，kmol/（m2·s）。

水组分的物质守恒方程相对简单，可以写成：

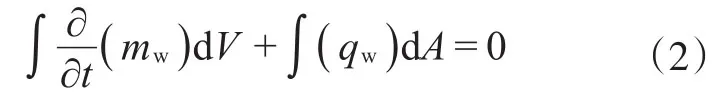
在裂缝中，组分c和水的守恒方程为:

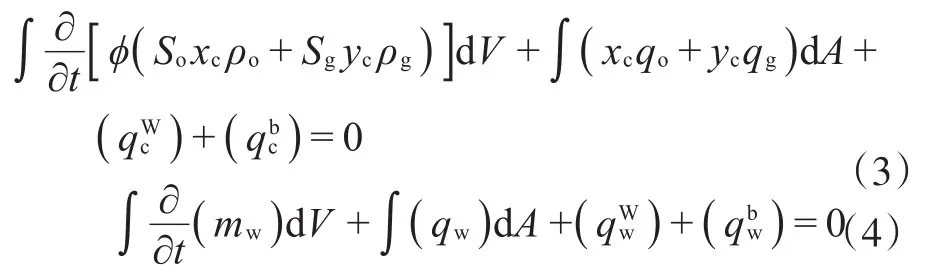
与基质中的守恒方程有所不同，裂缝中不需要考虑吸附解吸，但是由于裂缝与井筒，边界水体相连接，控制方程中需要综合考虑井筒和边界的影响。和分别为组分c和井及边界之间流动的摩尔流速，而和则为水和井及边界之间流动的摩尔流速。

基质和与之相连的裂缝之间的流动可视为相邻的2个控制体之间的流动，可以通过计算流动项得到。

为了确定各相中的摩尔分数，在进行数值模拟时还需要求解各相之间的溢度平衡方程：

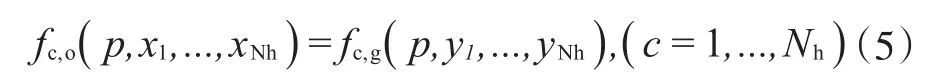
式中：fc,o和fc,g分别为组分c在油相和气相中的逸度，MPa。

通过相平衡计算获得组分c在油相和气相中的摩尔分数，然后根据气体状态方程可以求出气相和油相的压缩因子，进而更新各相密度和黏度。

2.2 吸附解吸模型

气体的吸附解吸是页岩气不同于常规气藏的显著特征之一。目前用来描述页岩基质气体解吸现象的最主要模型是Langmuire方程，Langmuire方程假设吸附为单分子层，最初被用来描述煤层气基质中的吸附解吸现象。对于单组分的气体而言，Langmuire方程可以表述为：

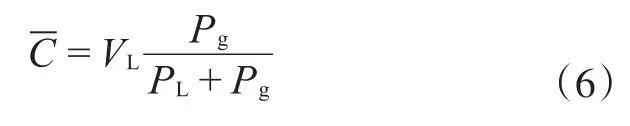
式中：Pg为气体的压力，MPa；PL为Langmuire压力，MPa；-C为平衡时的吸附浓度，mg/L；VL为Langmuire体积，m3。

VL是测试获得的最大气体吸附量，PL表示吸附量达到最大吸附量二分之一时的压力。当模型扩展至多组分模型时，Langmuire等温吸附模型的数学形式将转变为：

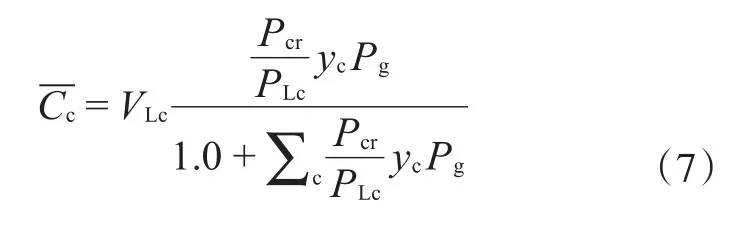
式中：Pcr为标况压力，MPa。

Langmuire等温系数模型中的Langmuire压力均可以通过对实验数据进行拟合获得。

通常情况下，气体从基质中解吸进入大孔的过程被假设为瞬时吸附过程，即压力发生改变,裂缝中的气体浓度瞬间达到平衡吸附浓度，但是事实上，由于页岩储层基质渗透率极低，解吸的气体从基质内的微孔扩散进入大孔需要一定的时间。根据菲克定律，单位体积基质内气体的扩散流量可以表示为：

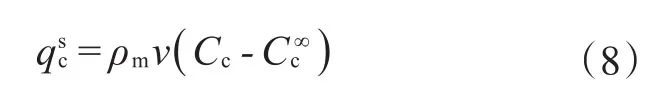
式中：qsc为组分c的质量流量，kg/s；ρm是基质的密度，kg/m3；Cc是基质当前的吸附浓度，mg/L；C∞c为当前状态下的平衡吸附浓度，mg/L。

平衡吸附浓度可以根据Langmuir等温吸附模型（式6）得到。扩散速度v衡量解吸气体扩散进入大孔速度快慢，可以通过对吸附体积—时间曲线进行拟合得到。

2.3 嵌入式离散裂缝模型构建基本流程

嵌入式离散裂缝（EDFM）将裂缝模拟为镶嵌在结构化网格中的四边形平板，基质网格仍采用结构网格，包括正交网格和角点网格。EDFM能模拟非常复杂的裂缝，还能保留裂缝的几何细节，又不会使基质网格变为非结构网格，结构网格索引起来更加方便。

EDFM的网格剖分、传导率计算流程如下：

①筛选所有与裂缝片有接触的基质网格；

②生成裂缝平面与基质网格的交面，这些交面有可能是三角形、四边形、五边形、六边形；

③根据裂缝外形剪裁交面；

④计算基质网格—多边形交面的传导率；

⑤搜索裂缝内部多边形的连接，计算多边形之间的传导率；

⑥搜索裂缝与裂缝的连接：首先求出裂缝与裂缝的交线，然后在2个裂缝中分别找到交线穿过的多边形，计算共享交线的多边形之间的传导率。

2.4 嵌入式离散裂缝模型传导率计算

计算“基质网格—交面”、裂缝内的多边形、裂缝与裂缝之间的多边形的传导率时，采用两点格式的传导率，是用于离散后的流动方程的传导率，用符号T表示，任意2个单元之间的流量都可以写为λT（p1-p2），其中λ是流度，T的单位是m·10-3μm2。多边形与多边形的传导率按二维网格的差分格式计算，由于多边形嵌入在六面体内部，基质网格（六面体）与多边形的传导率无法按常规方法计算，其具体计算方法为：

式中：A是多边形的面积，m2；km是基质渗透率，10-3μm2是基质网格到多边形的距离，m。

如果基质渗透率是张量，则传导率等于：

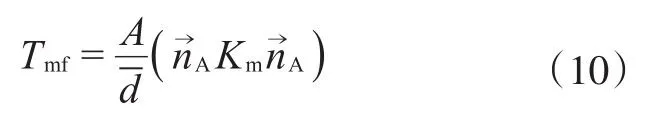
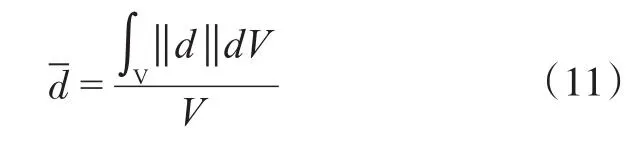
在编写计算代码时，式（11）的分子中的积分项可以转化为6个四棱锥到多边形的距离的加权平均，每个四棱锥的底分别是六面体的一个面，四棱锥的顶点都是多边形上的同一点，为了方便，就取多边形的第一个顶点。如图1所示，六面体到多边形KLMN的平均距离等于：

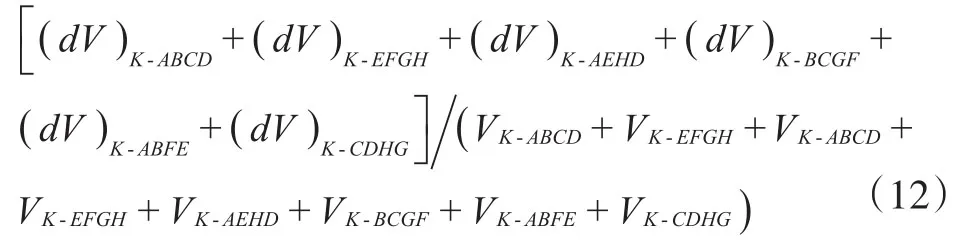
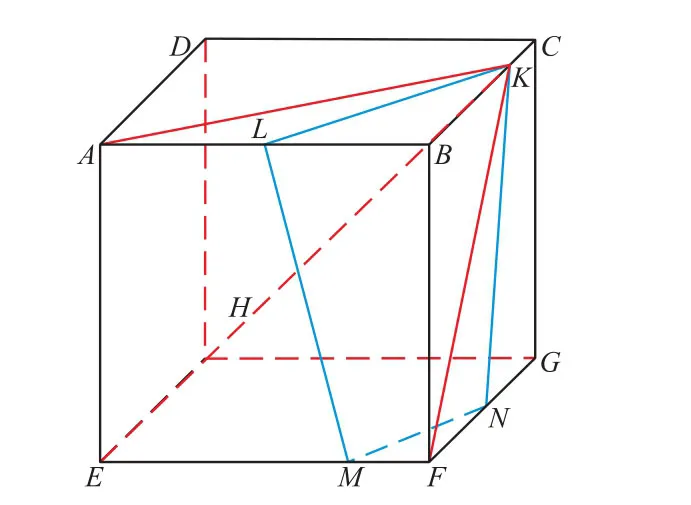
图1 计算基质网格到多边形KLMN的距离-dFig.1 Distance（）between matrix grid and polygonKLMN

在EDFM的代码实现中，与EDFM有关的搜索、离散和传导率计算都被整合到了模拟器内部。模拟器首先完成裂缝多边形生成，然后追加网格数量，并在基质网格的连接之后追加有关裂缝的连接。

如果井与嵌入式裂缝直接相连，则需要计算井与多边形的井指数，推导过程如下：

设井从多边形i穿过，用j表示多边形i周围的某个多边形（图2），设裂缝沿翼展方向的渗透率为kx、沿上下方向的渗透率为ky，由Peaceman的各向异性径向流公式，流入井的流量可以表达为：

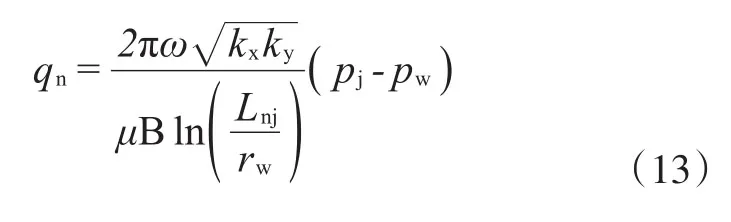
式中：qn为井产量，m3；pw为井的压力，MPa；ω为裂缝开度，m；B为体积系数，无因次；μ为黏度，mPa·s；rw为井半径，m。，(xnj,ynj)为连接穿孔位置n与多边形j的形心的向量。约等号右侧是Lnj的近似公式，在的范围内，公式的误差是非常小的。

接下来设法消去pj，根据多边形汇流公式，流入井的流量等于多边形i周围各多边形流入i的总流量：

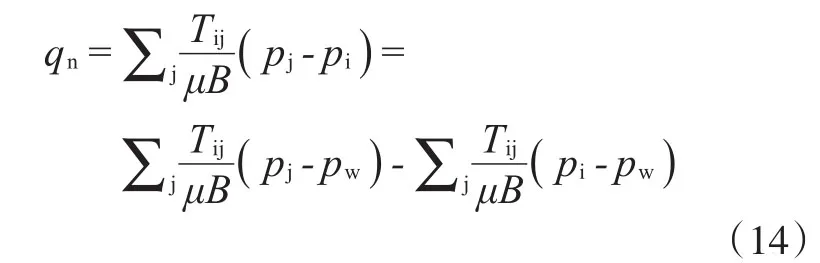
式中：Tij是多边形i、j之间的传导率系数

利用式（13）和（14）式消去pj，得到只关于qn，pw和pi的表达式：

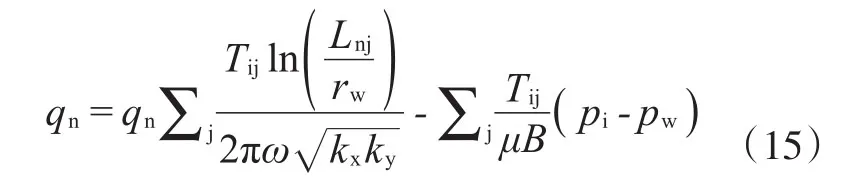
或者写为：

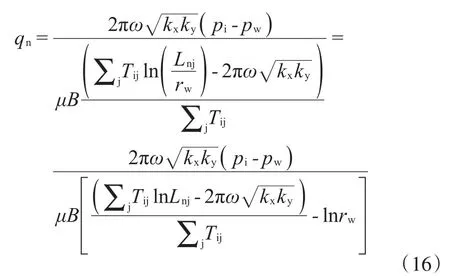
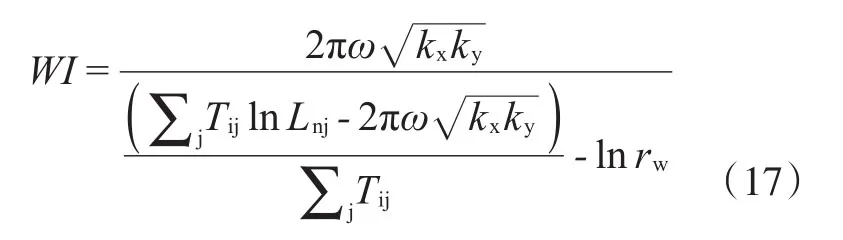
式中：WI为井指数。

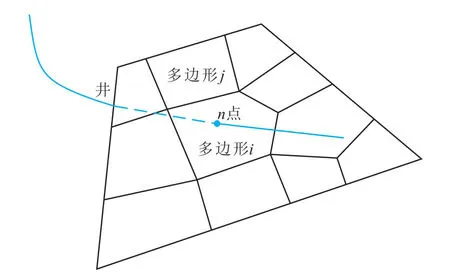
图2 井穿过裂缝多边形i，穿孔位置为n点Fig.2 Well penetrate the polygon（i）at the point（n）

可见井与裂缝多边形的井指数不仅与多边形本身有关，还与多边形周围一圈多边形有关，因为Tij、Lnj同时与多边形i和多边形j有关。

2.5 基于微地震的压后裂缝建模方法

由于微地震信号由天然裂缝激活后发生剪切形变释放，并不直接显示水力主裂缝的位置。因此，将基于微地震分别采用不同方法对天然裂缝网络和水力主裂缝进行裂缝建模。

激活的天然裂缝可以直接由微地震发生的时间序列来迭代生成。具体为，将同一压裂段的微地震事件按时间顺序排序，从第一个微地震事件开始，首先连接第一个事件点和第二个事件点生成第一条裂缝，然后在该裂缝上随机寻找一个起裂点，与下一微地震事件相连，最终形成整个压裂段的激活天然裂缝网络。水力主裂缝的产生引发了与之相连的天然裂缝激活过程，因此，微地震事件应分布在水力主裂缝周围。本项目研究中将采用最小二乘法来确定水力主裂缝位置，即在某一个压裂段内，所有微地震点到水力主裂缝的距离之和最小。

3 算例模拟结果

3.1 研究区基本情况

该研究区位于涪陵焦石坝区块，为五峰—龙马溪组一段，厚度约40 m。该储层页岩气TOC（总有机碳含量）大于2%，有机质类型为I和II1型，热演化成熟度Ro为2.2%～3.1%。孔隙度3.0%～0.5%，黏土矿物含量平均34.5%，脆性矿物含量60%～66%，以生物成因的石英为主，占石英总含量的2/3，可压性较好。测井总含气量2.51～7.92 m3/t，平均5.77 m3/t，地层压力系数介于1.25～1.55，保存条件较好。

3.2 地质模型建立

将剩余气的预测方法应用于A平台模拟该平台的储量动用状况。该平台共有3口分段压裂水平井，即A-1HF、A-2HF和A-3HF，3口水平井水平段长度分别为1 468 m、1 262 m、1 248 m，井距为600 m。该井平台共覆盖3.24 km2，属五峰—龙马溪组页岩储层，埋深为2 550 m，储层温度为85℃，储层共划分为9小层，①至⑤小层为开发储层，厚度为40 m，束缚水饱和度40%。用于数值模拟的数据均由涪陵现场通过测井和地球物理方法确定。根据实验数据确定涪陵区域页岩气等温吸附曲线参数，本平台模型Langmuire压力为6 MPa，Langmuire体积为2.1～3.6 m3/t，吸附气占40%左右。根据容积法，该平台①至⑤小层总储量为18.3×108m3，储量丰度5.88×108m3/km2，各层储量见表1。

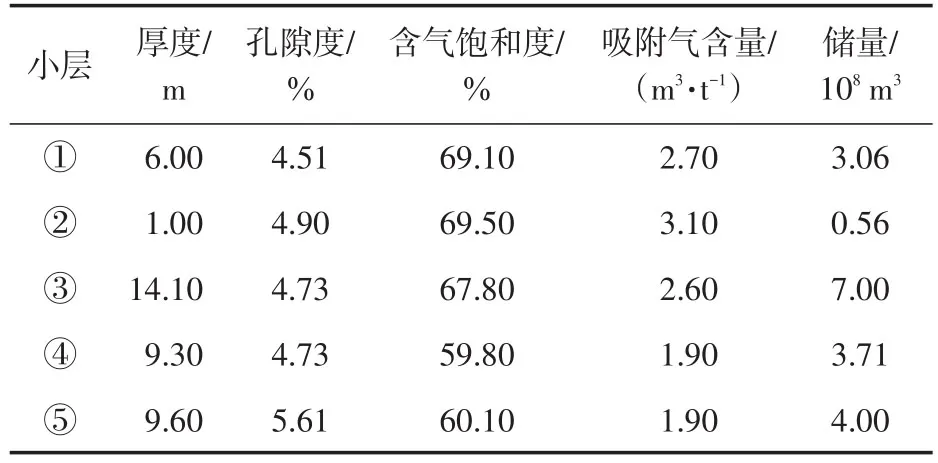
表1 ①至⑤小层储量信息Table1 Reserve information of layer①to⑤

建立A平台数值模型，该模型平面上均匀划分10 m×10 m的网格，纵向上共有9小层。整个模型总网格数为291 600。数值模型的具体参数见表2。

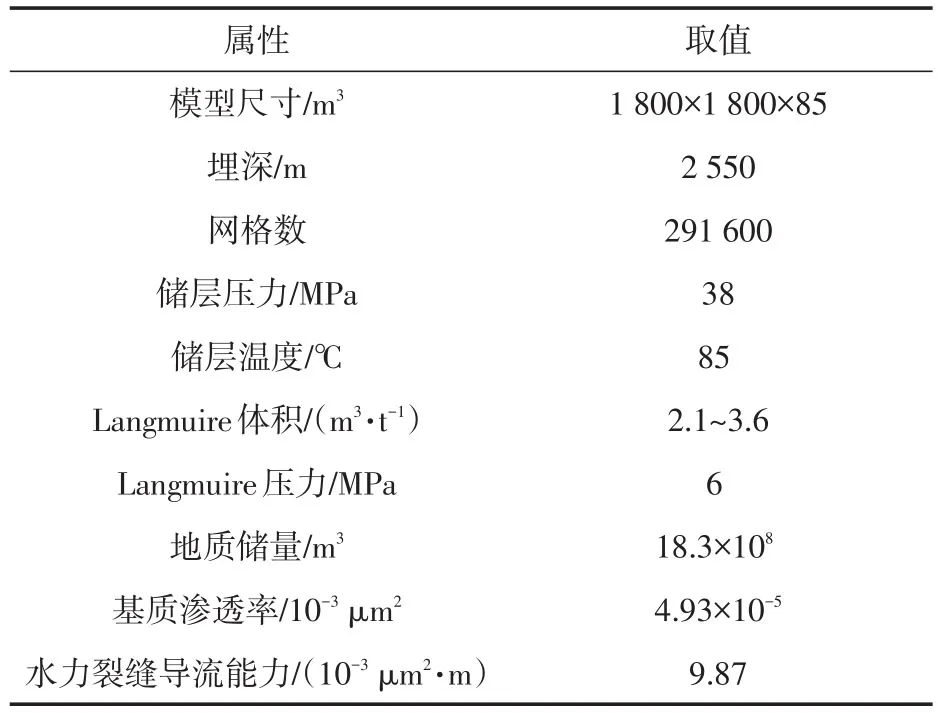
表2 数值模型初始参数Table2 Initial parameters of numerical model

3.3 基于微地震裂缝建模

A平台进行了微地震监测来探测裂缝的扩展。A平台微地震分布（图3），从俯视图看，微地震事件分布在井周围250 m以内，JYA-2HF和JYA-3HF微地震事件存在重合区域。

根据裂缝建模方法，建立A平台压后裂缝模型（图4）。3口分段压裂水平井分别拥有裂缝736，520，350条。由于微地震仅仅显示响应裂缝，实际返排后裂缝将发生闭合，实际有效裂缝半长将远远小于响应裂缝半长。在历史拟合过程中将把有效裂缝范围作为待定参数进行调整。根据微地震确定的裂缝缝高统计情况，和JY37-3HF相比，JYA平台缝高分布更加均匀，＜10 m，10～20 m，20～30 m，＞30 m的比例分别为34%、24%、24%和18%。

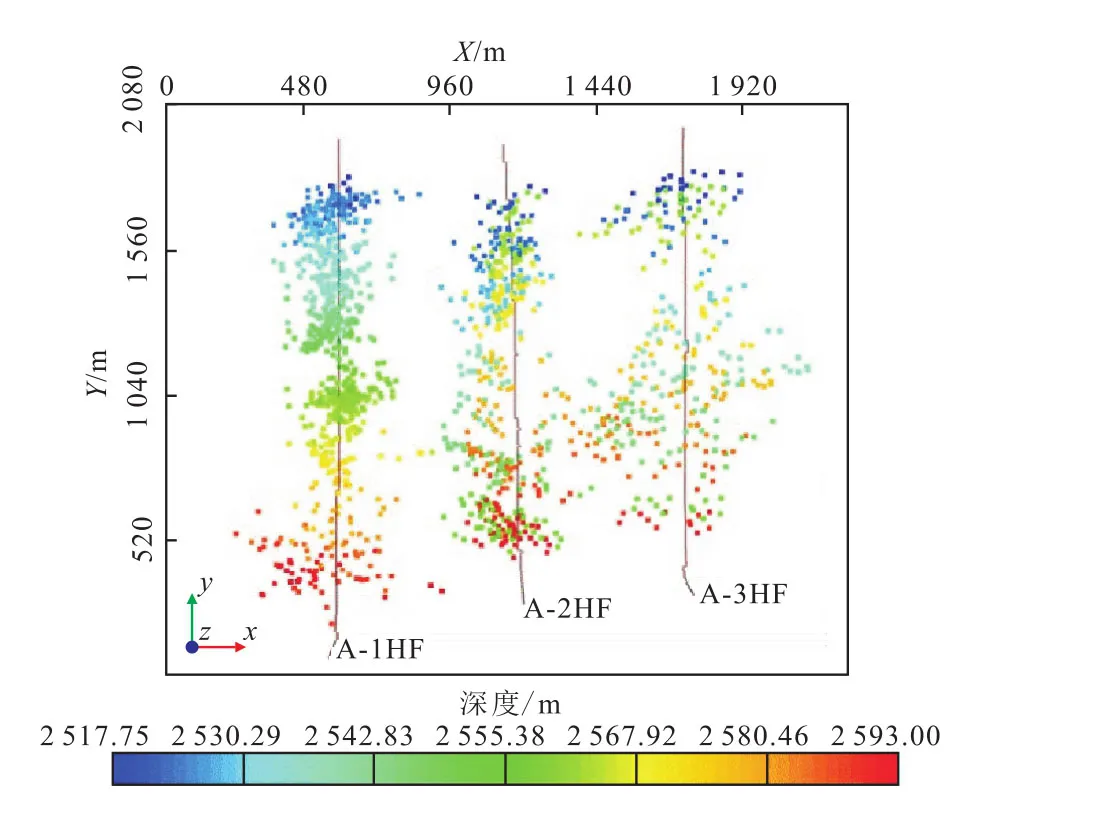
图3 JYA平台微地震分布Fig.3 Distribution of micro-seismic for JYA platform

图4 JYA平台压后裂缝模型（拟合前）Fig.4 Fracture model of JYA platform after fracturing（before history matching）

图5 三口井流压历史拟合结果Fig.5 Historical fitting results of flow pressure for three wells

3.4 历史拟合

建立JYA平台压后模型之后，对该模型进行历史拟合。根据实际生产850 d，拟合井底压力。拟合过程中着重调整三个参数即激活的天然裂缝导流能力，主裂缝导流能力及平均有效裂缝半长。由拟合结果（图5）可知，经过历史拟合，模型模拟得到的井底压力和实测井底压力基本吻合。根据历史拟合之后确定的模型参数（表3），裂缝有效半长较响应半长均有不同程度的缩小，其中JYA-3HF井缩小最为明显。拟合之后的裂缝模型见图6。对比微地震分布发现，尽管微地震响应区域有所重叠，但是JYA-2HF井和JYA-3HF井之间并未存在有效的裂缝沟通。

3口水平井生产850 d后5个小层剩余气的储量情况及动用面积见表4。总的来看，JYA-1HF井动用面积大于JYA-2HF井和JYA-3HF井。5个小层井控储量采出程度分别为11%、10%、10%、9%、8%，上部储层的采出程度小于下部储层。以①号小层为例（图7），改造区内平均地层压力降至20 MPa，采出程度约为28.9%，未改造区目前采出程度低。目前JYA-1HF井和JYA-2HF井之间存在宽为200～400 m的未动用区域，JYA-2HF井和JYA-3HF井间存在宽为100～400 m的未动用区域。

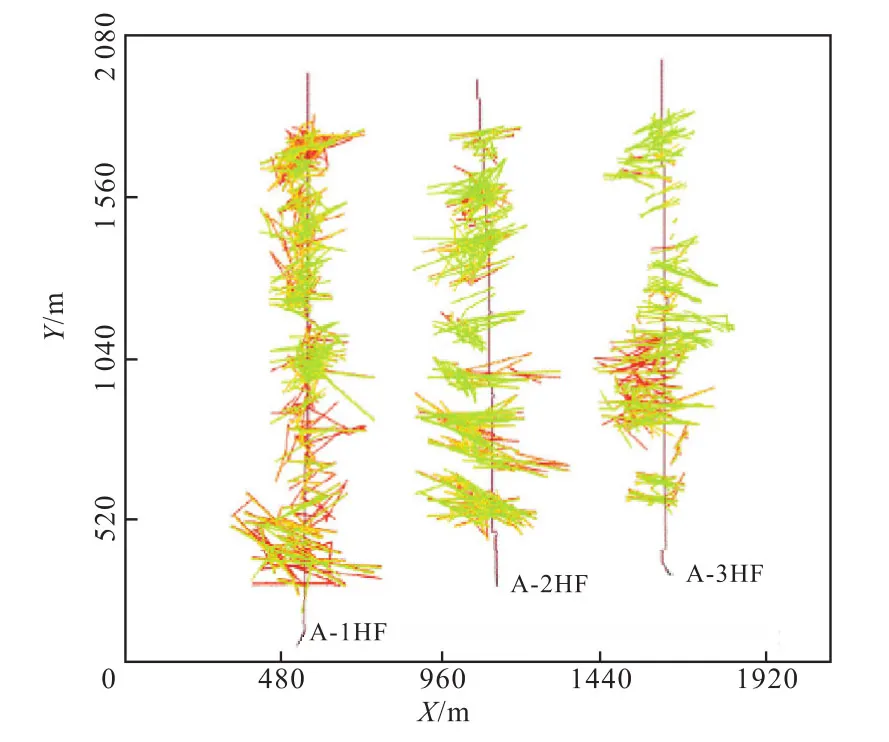
图6 历史拟合后压裂裂缝模型Fig.6 Fracture model after historical fitting

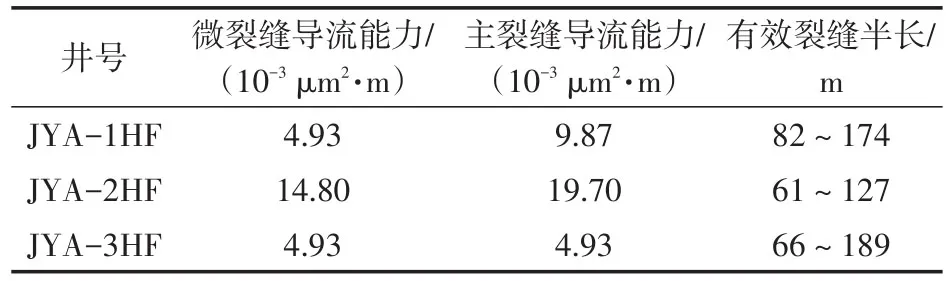
表3 JYA平台拟合后模型参数Table3 Model parameters after fitting of JYA platform

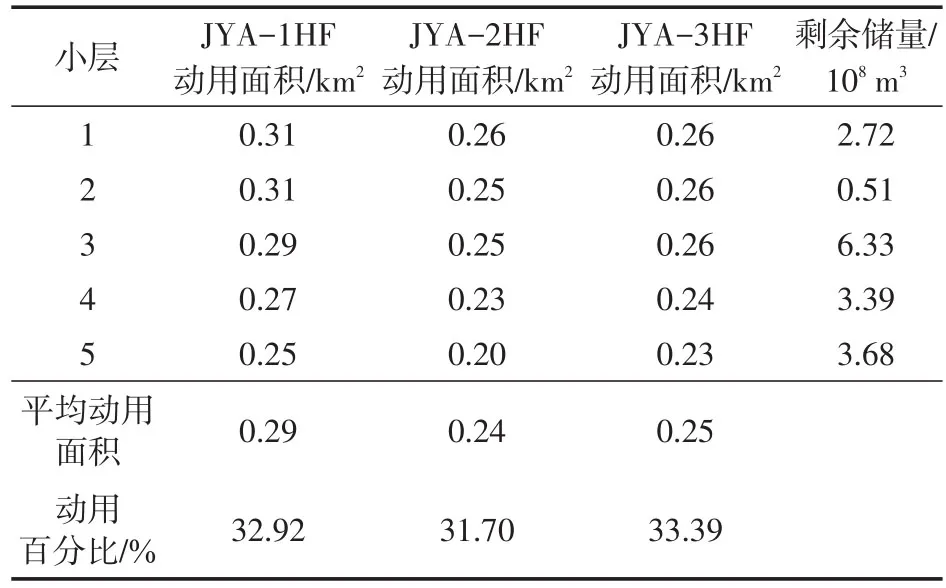
表4 生产850 d后5层储量动用情况（压降大于10 MPa）Table4 Reserve utilization of five layers after 850 days’production（pressure drop is larger than 10 MPa）

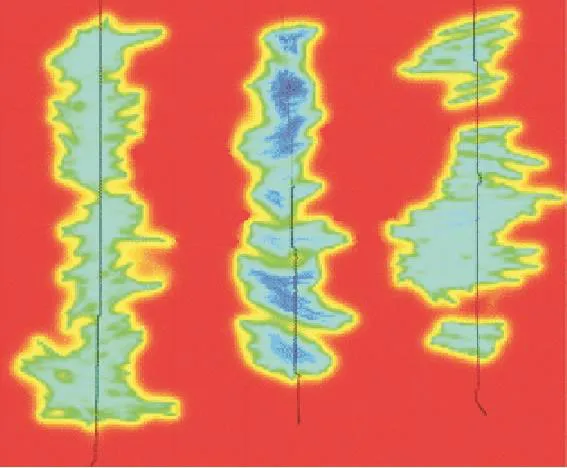
图7 ①号层压力分布Fig.7 Pressure distribution of layer①

3.5 加密效果模拟

在JYA-1HF井、JYA-2HF井和JYA-3HF井之间各部署一口加密井JYA-4HF井、JYA-5HF井。加密井距JYA-1HF井和JYA-2HF井距离为300 m。JYA-4HF井、JYA-5HF井水平段长度1 500 m，共压裂20段，段间距80 m，裂缝半长100 m，其他所有参数参照JYA-1HF井。通过数值模拟预测30年后的全区块产能，评价加密效果。在2.6 G Hz CPU，8 G内存计算机上进行加密之后的模型模拟，模拟时间30年，计算时间为946 s。

对比加密前，JYA-1HF井和JYA-2HF井之间压力下降更为明显（图8），说明井间未动用区域得到了很好地动用。表5展示的是该平台5口井加密前和加密后产能对比。加密后原来动用较差区域的采出程度大幅提升60%左右，对比加密前后，加密井干扰使原来3口井总EUR（预计最终采收率）降低0.22×108m3，但加密后5口井总EUR提升1.66×108m3，新井平均EUR为0.94×108m3。由此可见，加密井部署可以显著提升井间难以动用区域的储量动用程度，提高采收率。

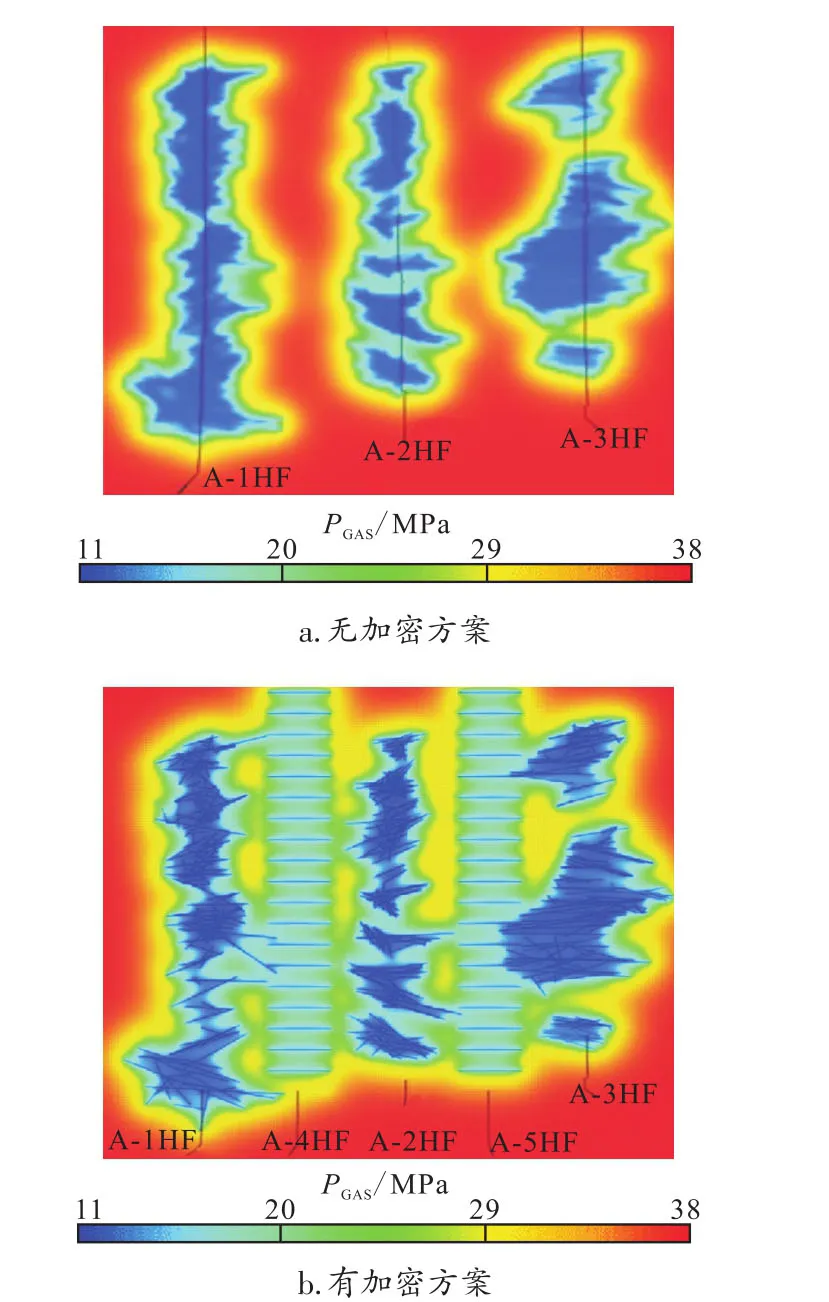
图8 有加密和无加密方案30年末压力分布Fig.8 Pressure distribution after 30 years with or without infill wells

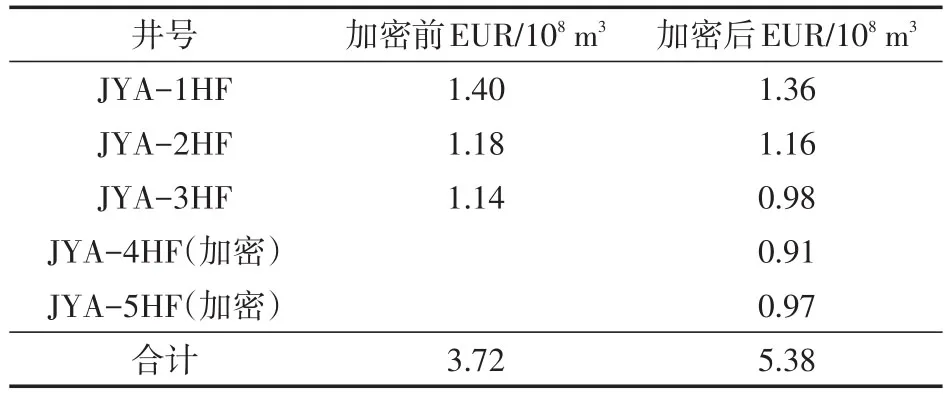
表5 加密前后各口井产能对比Table5 Comparison of EUR before and after placement of infill wells

4 结论

1）提出一种可以处理分段压裂水平井开发的页岩气渗流模拟的方法。该方法适用于采用多段压裂水平井开发的页岩气藏。该方法将裂缝视为嵌入至结构化储层网格的矩形裂缝片。裂缝片与储层网格之间的流动则通过计算非相邻连接确定。

2）嵌入式离散方法与传统基于双孔双渗模型的数值模拟方法相比，可以更加准确地刻画裂缝的展布，从而使得最终的模拟结果能够更加准确地反映压裂缝网非均质分布对水平井产量及储存动用情况的影响。

3）微地震监测是监测压裂裂缝展布的重要手段，提出了一种新的基于微地震监测数据构建压后模型并进行数值模拟的方法。基于该方法，准确模拟了涪陵某井平台3口压裂水平井的产能、储量动用情况。模拟结果显示，开发过程中实际有效压裂裂缝的分布范围小于微地震响应范围。生产30年后，两水平井间仍然存在宽度为100～300 m的区域储量没有动用，该部分储量可以通过部署加密井加以开采。为该平台下一步调整方案的制定提供了技术支持。