非饱和加筋土挡墙稳定性分析

2019-11-11赵斌凯林永亮

铁道建筑 2019年10期

赵斌凯，林永亮

（上海大学土木工程系，上海 200444）

由于加筋土挡墙在施工中通常采用水平分层填筑、加筋、压实的方法，传统的竖向条分法对于分析加筋土挡墙内部的稳定性问题存在明显弊端。因此，文献［1-3］提出水平条分法的思想用来分析加筋结构。文献［4］基于拟静力法，采用水平条分法推导出挡墙内部稳定所需筋材拉力总和及筋材长度。文献［5］也基于拟静力-水平条分法，研究加筋土挡墙填土内摩擦角、黏聚力、水平地震力加速度系数、挡墙倾角、滑动体上部荷载等参数对地震稳定性（所需筋材拉力总和）的影响。文献［6］突破拟静力法的局限，采用拟动力法和水平条分法推导出筋材拉力及临界破裂角公式并进行参数分析。文献［7］考虑了地下水对加筋土挡墙稳定性的影响。以上研究均认为填土处于饱和状态，未考虑土体非饱和特性对稳定性的影响。

实际上，在我国的干旱及半干旱地表附近，土体多处于非饱和状态［8-9］；而非饱和土中由于吸力的存在，其强度远大于饱和土。故而在实际工程中应充分考虑非饱和特性，方能充分发挥土体的真实强度潜能。因此，本文针对非饱和加筋土挡墙，采用水平条分法，建立2 种不同基质吸力分布情况下筋材拉力总和及筋材长度的解析公式，并对公式实际应用情况进行探讨，最后分析土体的非饱和特性（基质吸力、吸力分布状况与吸力角）对筋材拉力总和与筋材长度的影响，所得结论对非饱和加筋土挡墙的设计与施工具有一定的指导意义。

1 非饱和加筋土挡墙稳定性评价模型

1.1 基本假定

根据GB/T 50290—2014《土工合成材料应用技术规范》和SL/T 225—98《水利水电工程土工合成材料应用技术规范》，筋材挡墙的潜在破裂面为朗肯破裂面，如图1所示。图中：H为挡墙高度；hi为第i层筋材距墙顶距离；La为筋材无效长度；Lc为筋材锚固长度；L为筋材总长；li为第i水平土条与破裂面交线长度；α为挡墙破裂面与水平面的夹角；FN为加筋土挡墙活动区内土体上部所受均布荷载；φ为土体的内摩擦角。

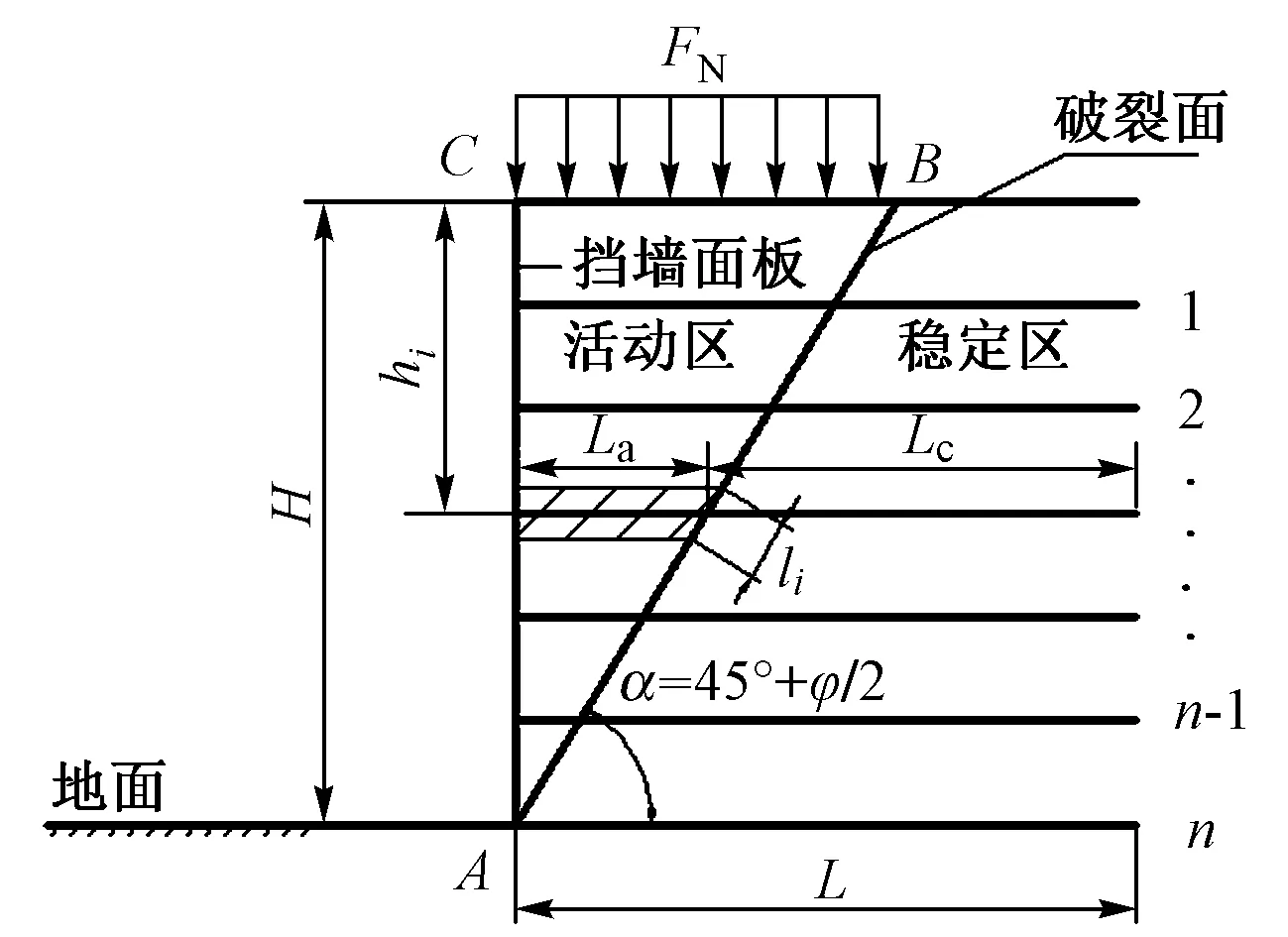
图1 加筋土挡墙计算示意

挡墙填土为非饱和土，填土中基质吸力沿挡墙高度均匀分布，或线性减小至挡墙底部，如图2所示。图中，u0为挡墙顶部填土的基质吸力，称为初始基质吸力；ua为孔隙气压力；uw为孔隙水压力。当基质吸力沿挡墙高度线性减小至挡墙底部时，挡墙任意高度处填土的基质吸力ui为

图2 基质吸力分布

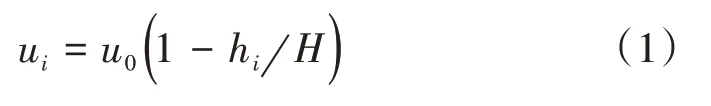
1.2 强度理论

破裂面抗剪强度τf与剪切应力τr的比值，即安全系数FS

非饱和土的抗剪强度τf采用Fredlund 双应力状态变量强度公式［10］，即

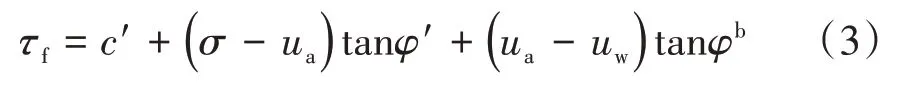
式中：c'为有效黏聚力；φ'为有效内摩擦角；σ为总法向应力；（σ-ua）为净法向应力；（ua-uw）为基质吸力；φb为吸力角，取值小于或等于有效内摩擦角φ'，且与基质吸力有关。

当土体饱和时，气体溶解于水，即ua=uw。此时，非饱和土的抗剪强度公式（3）退化为式（4）。

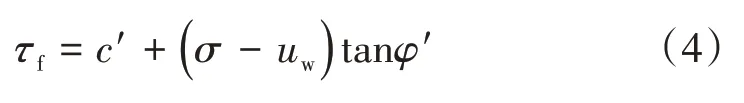
1.3 计算模型

将加筋土挡墙内部潜在的滑动体ABC分割成n个水平土条，每个土条包含有1 层筋材（参见图1），第i个水平土条的受力简图如图3 所示。图中：Wi为土条自重；FN，i，FN，i+1为水平土条上下两侧的法向力；Ft，i，Ft，i+1分别为切向力；NN，i，Nt，i分别为滑动面的法向反力与切向反力；Ti为第i层筋材的拉力；Di为第i层水平土条的高度，大小与筋材的竖向间距有关。

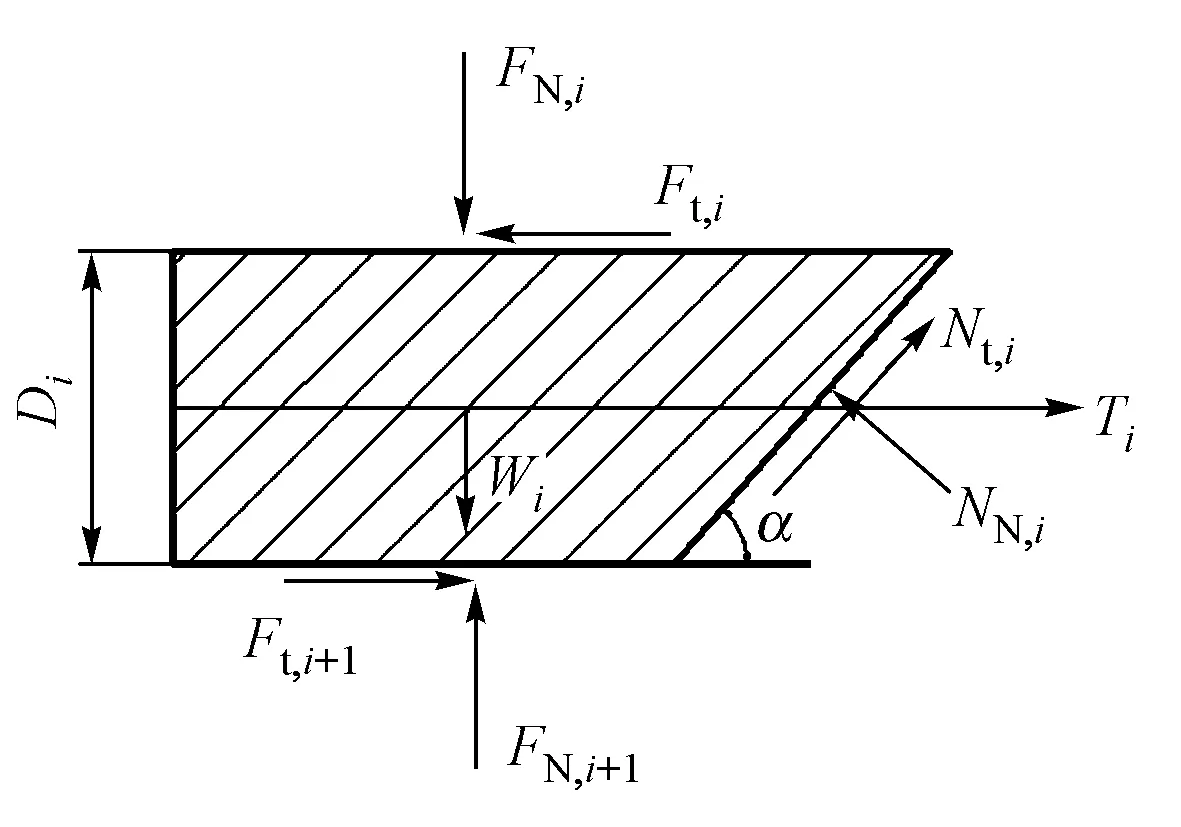
图3 第i层水平土条受力简图

以第i层水平土条为研究对象，受力平衡时其竖向分量为零，即

结合式（2）、式（3），可知第i层土条破裂面上的剪力为

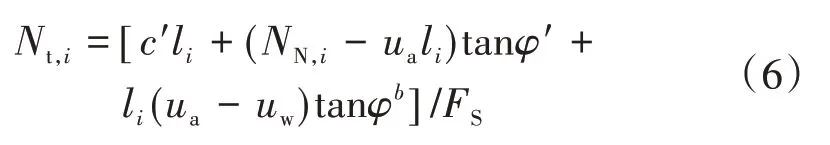
将式（6）代入式（5）得：

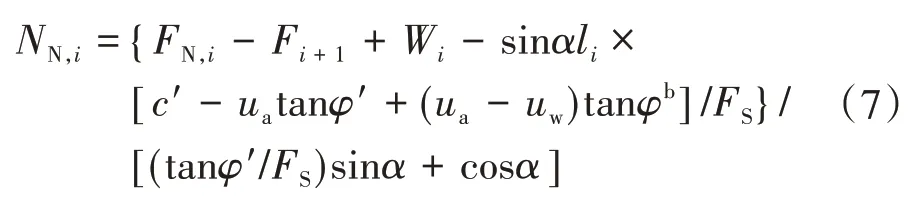
以整个滑动体ABC 为研究对象，滑动体受力平衡时水平分量为零，即

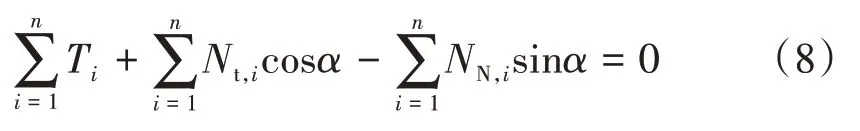
结合式（6）、式（7）及式（8），可得总加筋力为

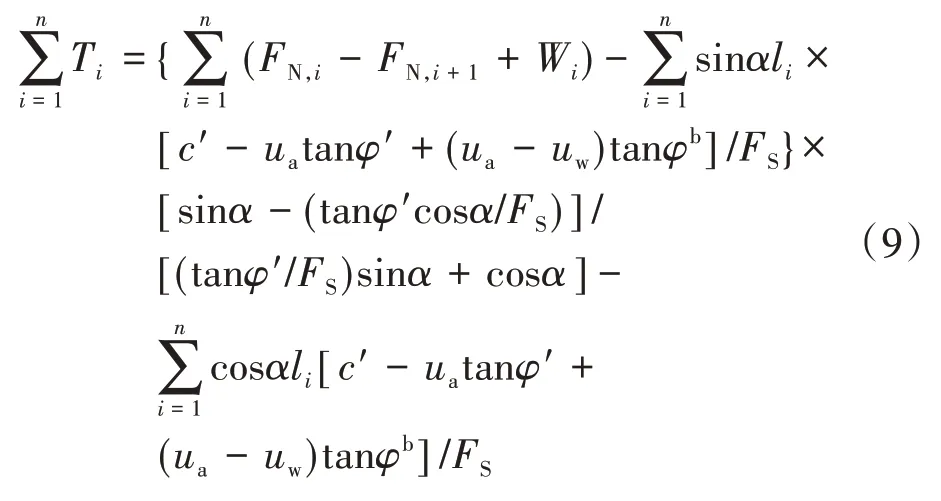
1.3.1 基质吸力均匀分布

根据式（9），可得到基质吸力沿挡墙高度均匀分布时挡墙内部稳定所需筋材总拉力为

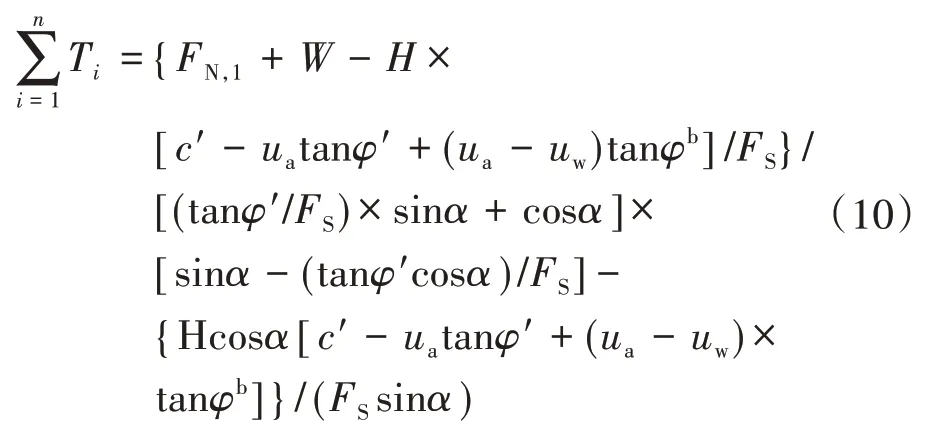
式中：FN，1为墙顶超载，大小为图1所示均布荷载；W为滑动体ABC的重量，W=γH2/(2tanα)，γ为填土重度。

1.3.2 基质吸力线性分布

结合式（1）和式（9），可得基质吸力线性减小时挡墙内部稳定所需筋材总拉力为

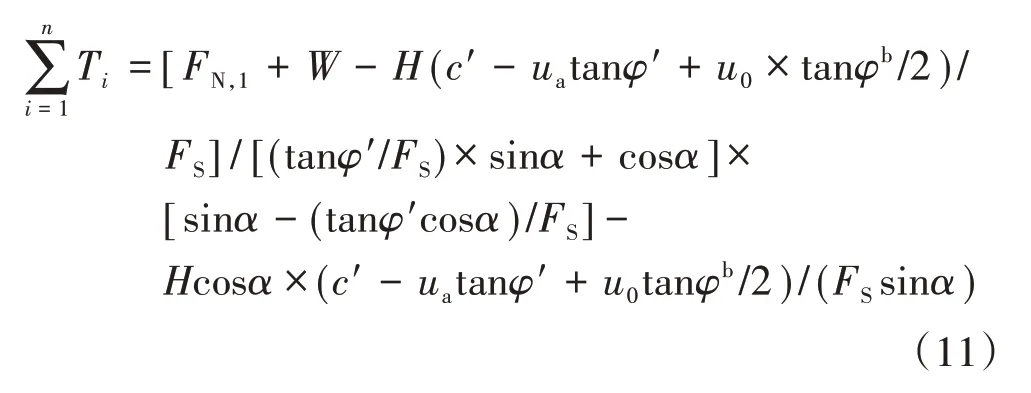
1.4 筋材长度计算

利用参数K可以实现挡墙内部稳定所需筋材拉力总和的无量刚化

式中，K为挡墙内部稳定所需筋材拉力总和参数。

当挡土墙处于极限平衡状态时，挡墙稳定区的土体将发生筋土界面的黏着破坏，此时筋材的抗拔力由筋材锚固段筋土界面摩擦力提供［12］。以第i层筋材的锚固段为研究对象，受力分析可以得到筋材的锚固长度Lei为

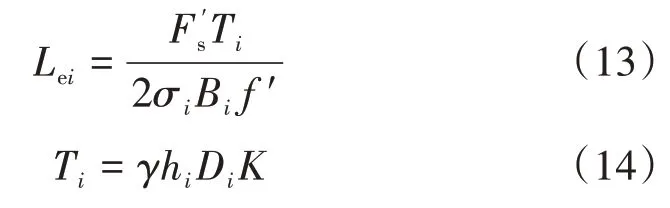
将式（14）代入式（13），则第i层筋材的锚固长度为

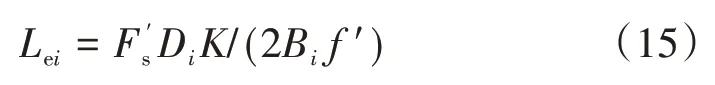
由图1 可知，筋材长度由挡墙活动区的无效长度Lai和稳定区的锚固长度Lei组成，则第i层筋材长度

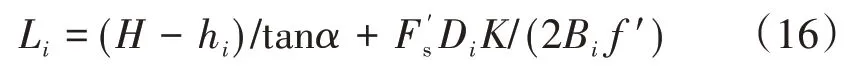
非饱和加筋土挡墙内部稳定所需筋材长度为各层筋材长度Li的最大值，并且利用挡墙高度H可以实现无量纲化，即

式中，Lc为筋材长度参数。

由式（16）、式（17）可知，参数Bi和Di，也就是筋材的配筋情况（筋材的水平间距、竖向间距，筋材截面）与筋材长度密切相关。

2 对模型的讨论

本文考虑了挡墙填土的非饱和土特性，即基质吸力与吸力角（大小及分布情况），建立了挡墙内部稳定所需筋材总拉力式（10）与式（11）。

当挡墙填土为饱和土，即均布基质吸力ua-uw=0或初始基质吸力u0=0时，式（10）与（11）可退化为

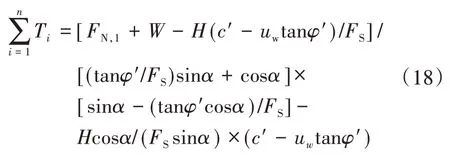
式（18）即为填土为饱和土时挡墙内部稳定所需筋材总拉力计算公式［4］。

当挡墙填土的孔隙水压力uw=0 时，式（10）可简化为

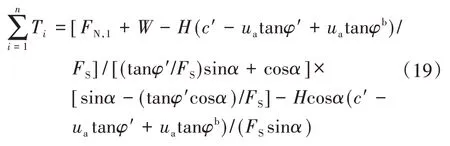
式（19）即为填土为干土（砂）时挡墙内部稳定所需筋材总拉力计算公式。因此，本文所得到的挡墙内部稳定所需筋材总拉力公式，是对传统的饱和土挡墙的进一步深化，具有广泛的适用性，一般工程条件都能得到理论解答，而不是仅仅局限于理想的饱和土状态。同时，也验证了本文所得到的解析公式的正确性。

3 参数影响特性

为研究挡墙填土的非饱和特性对挡墙内部稳定性的影响特性，以上述挡墙为研究对象，并假定挡墙填土为非饱和土。参数分析的前提条件为：墙顶超载FN，1=0，加筋土挡墙高H=5 m，填土重度γ=18 kN/m3，有效黏聚力c'=0，有效内摩擦角φ'=20°，吸力角φb=16°，孔隙气压力ua=100 kPa，安全系数FS=1.0；假设挡墙筋材是等间距分布的，竖向间距0.5 m，则每层水平土条的高度D=0.5 m；水平间距0.09 m，筋材宽度0.01 m，则单位宽度挡墙内每层筋材的总宽度B=0.1 m；筋土界面摩擦系数f'=0.9；抗拔稳定性安全系数F's=1.0。

3.1 基质吸力

以基质吸力作为参数分析的变量，假定均布基质吸力（ua-uw）与初始基质吸力u0的取值为0～100 kPa。

挡墙内部稳定所需筋材拉力总和参数K以及筋材长度参数Lc随基质吸力的变化关系见图4。

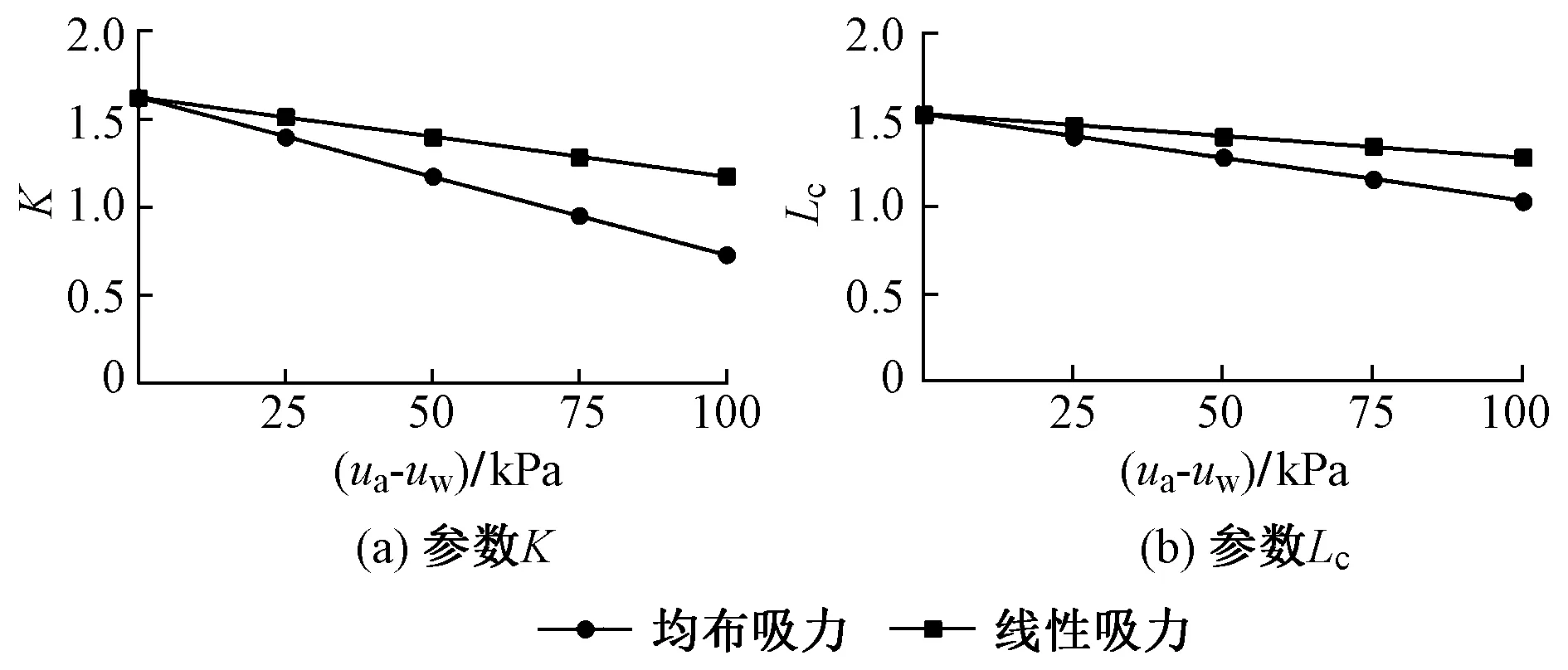
图4 基质吸力对参数K和Lc的影响

由图4可知：当基质吸力沿墙高度均匀分布，且从0逐渐变化到100 kPa时，参数K减小了55.0%，参数Lc减小了32.4%；而对于基质吸力沿墙高度线性减小的情况，参数K相应减小27.5%，参数Lc减小了16.2%。均匀分布时基质吸力对参数K、参数Lc的影响是线性分布时影响的2 倍；基质吸力对参数K的影响比对参数Lc的影响大。当基质吸力相同时，均布吸力的参数K、参数Lc比线性分布的小，换言之，基质吸力线性分布时的计算结果更为保守。此外，当基质吸力为零时，非饱和土退化为饱和土，参数K及参数Lc均为固定值。因此，在实际工程中，基质吸力的具体分布情况应根据工程地质情况作出合理假定。

3.2 吸力角

吸力角φb是非饱和土强度的重要参数，其值小于或等于有效内摩擦角φ'。挡墙填土的有效内摩擦角φ'为20°，因此吸力角φb在10°～18°取值。

2种基质吸力分布情况下筋材拉力总和参数K、筋材长度参数Lc与吸力角的关系见图5。

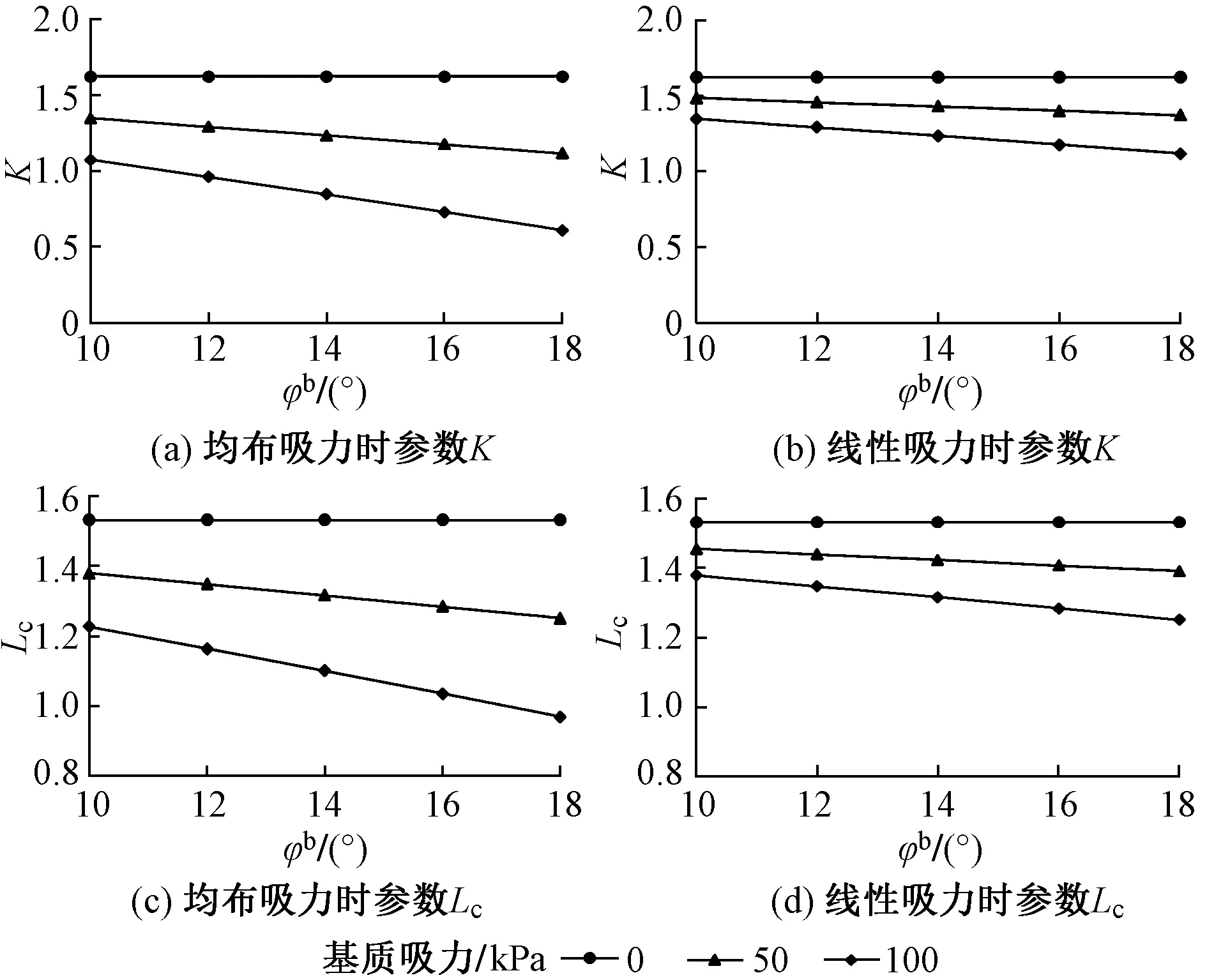
图5 不同基质吸力分布时吸力角对参数K和Lc的影响

由图5 可知：①当基质吸力为零时（填土为饱和土），参数K，Lc值为常数，与吸力角φb无关；②随着φb的增加，参数K，Lc值逐渐减小；③基质吸力沿挡墙高度均匀分布时，φb=18°时参数K比φb=10°时减小了17.1%（基质吸力为50 kPa）和43.0%（基质吸力为100 kPa），φb=18°时参数Lc比φb=10°时减小了9.3%（基质吸力为50 kPa）和20.9%（基质吸力为100 kPa）；④当基质吸力线性分布时，φb=18°时参数K值比φb=10°时减小了7.8%（基质吸力为50 kPa）和17.1%（基质吸力为100 kPa），φb=18°时参数Lc比φb=10°时减小了4.4%（基质吸力为50 kPa）和9.3%（基质吸力为100 kPa）；⑤均匀分布时吸力角对参数K，Lc的影响是线性分布时影响的2 倍；吸力角对参数K的影响比对参数Lc的影响大。由此可见，吸力角φb在基质吸力均匀分布且基质吸力较大时对参数K，Lc值的影响较为显著，设计加筋土挡墙时应考虑φb的影响。