“阶跃式”滑坡突变预测与核心因子提取的平衡集成树模型
2019-11-11何少其刘元雪赵久彬
何少其,刘元雪,梁 叶,刘 娜,赵久彬
(1.陆军勤务学院岩土力学与地质环境保护重庆市重点实验室,重庆 401311;2.重庆市地质矿产测试中心,重庆 400042;3.重庆长江勘测设计院有限公司,重庆 401147)
0 引言
“阶跃式”滑坡是三峡库区的典型滑坡类型[1],具有分布广泛、危害性大、成因复杂、难以预测等特点[2]。大量研究表明,库区降雨和水位升降是引起此类滑坡失稳的主要诱因[3-4],受此影响滑体的位移时间曲线呈现突变与稳定交替的演化形态,而突变又与稳定性下降直接相关[5]。因此,利用海量的位移和环境数据进行分析、挖掘是研究和预防此类滑坡灾害的有效途径[6],其中提升突变的预测精度和确定核心相关因子是关键问题。
近年来,“阶跃式”滑坡研究分析多以位移预测为主,应用了时间序列、支持向量机、神经网络等算法及其组合。彭令等[7]、MIAO F S等[8]分别利用时间序列将位移分解,并通过多项式函数和支持向量机耦合模型分别对趋势项和季节项进行拟合,并有效应用于总位移预测;李骅锦等[9]提出了ARMA与LASSO-ELM的联合模型,并选取Copula函数对诱因数据与位移预测数据的联合分布进行描述并提取诱因阈值和位移风险值;杨背背等[10]通过多项式拟合趋势项位移、LSTM模型拟合周期项位移,获得了预测精度较高的叠加动态模型。这类方法应用于滑坡位移跟踪时能够达到较高精准度,但多适用于单滑坡体预报,难以获取共性规律。与此类方法不同的是,文章提出了考虑高维地质环境影响因子作用下区域内“阶跃式”滑坡突变与稳定的分类优化模型,目前类似的思想和方法还不多见。
从数据层面来看,“阶跃式”滑坡的突变和稳定数据在数量上存在严重的不平衡问题,势必引起分类器性能下降。针对此类问题,CHAWLA N V等[11]提出了合成少数类过采样技术(Synthetic Minority Over-sampling Technique,SMOTE),HAN H等[12]通过增强分类边界附近少数类过采样得到改进的borderline-SMOTE算法。从分类器层面来看,单分类器如k近邻(KNN)、支持向量机(SVM)、逻辑回归(LR)、朴素贝叶斯(NB)、决策树(CART)等精度受限,且易造成模型过拟合。而随机森林(Random Forest,RF)[13]和梯度提升树(Gradient Boosted Decision Tree,GBDT)[14]这两种集成树算法利用了算法集成的思想,具有泛化性能优、精度高、计算速度快、多分类预测等优势。
基于以上考虑,本研究设计的平衡集成树,就是通过borderline-SMOTE中的1型(简称borsmote1) 合成控制适当比例的边界突变少数类以平衡数据源,对随机森林和梯度提升树进行优化;设计分层十折交叉验证和网格搜索的组合,利用剪枝提升泛化性能,最终使集成树提升至较高预测精度的平衡状态;结合海量“阶跃式”滑坡数据集,对多源异构数据进行归一化处理并用于训练与测试,结果评估利用了监督学习中的受试者工作特征(Receiver Operating Characteristics,ROC)标准[15],并定义综合精度平均值指标,模型得出的预测性能整体优于单集成树以及平衡前后的不同分类器;以树节点纯度计算对26个地质环境因子进行了排名,相比于常用的相关性系数,能够有效提取出核心影响因子。通过平衡集成树算法,使“阶跃式”滑坡的突变预测达到了较高的预报水准,确定出的核心相关因子可作为后续机理研究参考分析,为区域内滑坡理论分析与防治提供新的思想与方法。
1 平衡集成树算法
平衡集成树模型融合了borsmote1与集成树的算法优势,并结合实际的“阶跃式”滑坡数据进行应用。它的主要思想是利用训练集突变样本合成边界少数类,使数据达到测试分类性能最佳的平衡状态,从而对RF和GBDT进行改进和优化,并建立该状态下的最终模型。
1.1 数据平衡规则
传统的过采样和欠采样方法或造成模型的过拟合、或以牺牲大量宝贵数据为代价,均难以满足数据激增的发展趋势。因此,本文采用突变边界样本合成的方法平衡数据层。具体规则为:
(1)“阶跃式”滑坡数据全集为T,突变样本集合为P={p1,p2,…,ppn},稳定样本集合为N={n1,n2,…,nnn},其中pn和nn分别为突变样本和稳定样本的数量。在T范围内寻找P中所有样本pi(i=1,2…,pn}的m最近邻,m′是m最近邻中稳定样本数。
(2)当m′=m,表明pi被多数类样本完全包裹,此时被判别为噪声点;当m′∈[m/2,m),表明pi的m最近邻中稳定样本多于突变样本,突变极大可能被错分为稳定,此时被判别为危险点;当m′∈[0,m/2),表明pi的m最近邻中突变样本多于稳定样本,此时被判别为安全点。
(3)在广义欧式空间中,危险点即是P的边界样本,记为p*。
(4)通过不同比率调节对p*随机选取的最近邻中k个突变样本pj,按照公式(1)合成属于突变类的新样本pnew,所有新样本加入P组成新的合成突变样本集合Pnew。
pnew=p*+rand×(pj-p*)
(1)
式中,rand——在区间(0,1)内的随机数,j=1,2,…,k。
1.2 集成树参数优化
集成树参数优化的目标是改善集成树的普适性与鲁棒性,有效保证其对新数据的预测精度。对于RF和GBDT两种集成树而言,已被证明子树的数量越多,对随机状态的适应过程越稳定,但是训练和预测时长相应增加。通过实际测试与权衡,本研究均使用300棵子树用于集成树构建。由于GBDT采用了Boosting[16]的策略,利用损失函数(Loss Function)在梯度下降方向持续迭代提升模型准确率,本文通过设置学习率为0.1来调节减少残差的速率。同时,为了模型达到最优泛化的目的,根据机器学习经验法则拆分出总数据集的25%作为测试集,测试集不参与模型的训练过程,只在最后用于评估训练模型对于新数据的泛化表现。训练过程中,采取分层十折交叉验证和网格搜索手段来综合选择划分特征子集、控制树的深度等进行参数调优,对子树进行预剪枝操作。选取对高维多噪音数据次敏感的基尼系数(Gini Impurity)作为纯度计算标准,节点不纯度值越低,模型拟合越好。
1.3 计算方法
平衡集成树模型应用于“阶跃式”滑坡突变预测与特征提取的计算方法为:
(1)将多源、海量、异构数据归一化为可挖掘的数据信息,构建原始数据集,并拆分为训练集和测试集;
(2)训练集通过不同比率参数合成突变边界少数类样本,得到平衡化数据集,供RF、GBDT训练模型;
(3)以测试集综合精度平均值为评估指标,选定最佳测试精度下的参数优化组合,建立平衡集成树模型;
(4)预报区域内“阶跃式”滑坡突变,根据模型特征重要性提取核心相关因子(图1)。
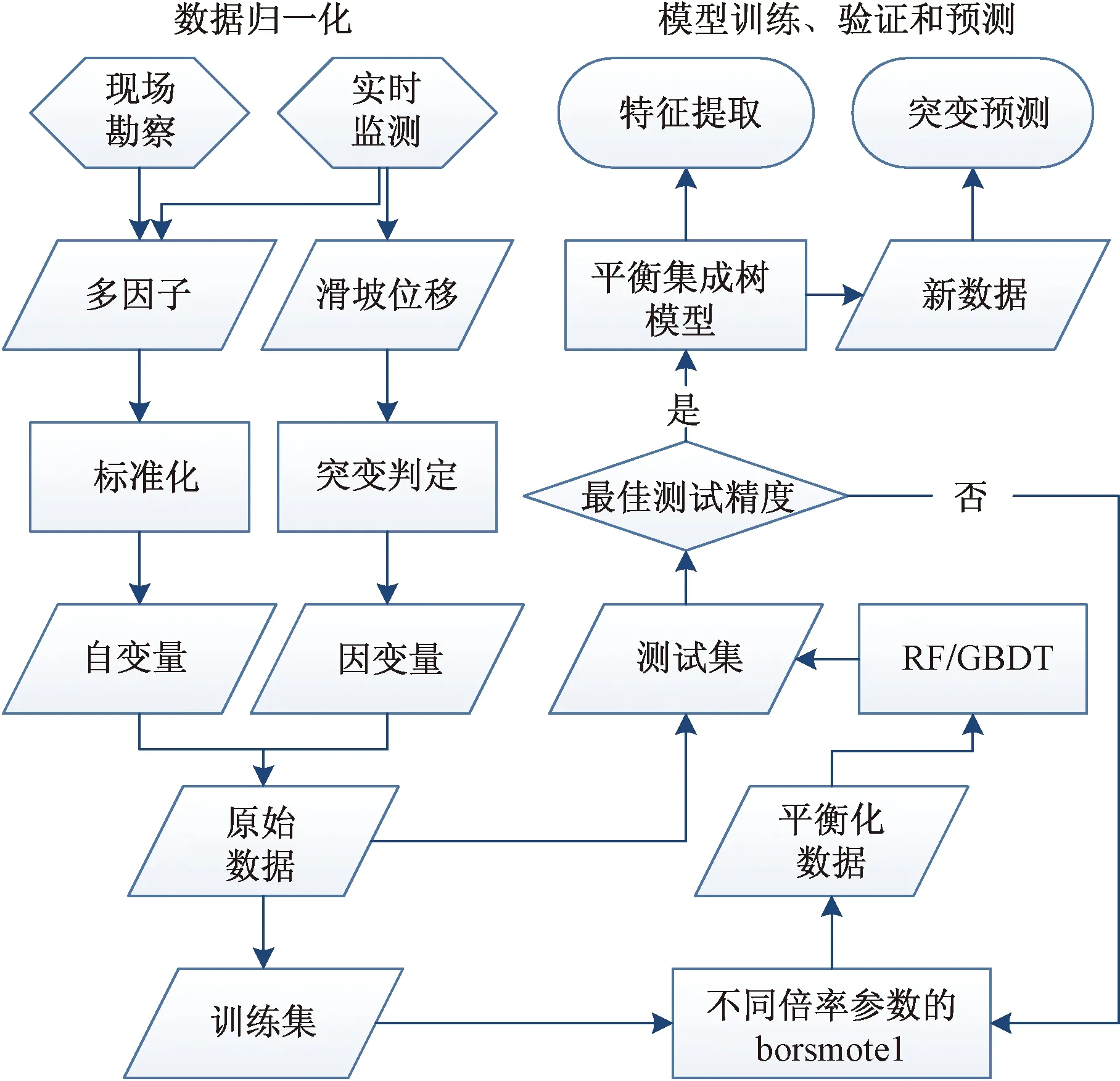
图1 平衡集成树模型流程Fig.1 Flow chat of the balanced decision tree ensemble model
1.4 评估指标
结合滑坡预测的实际情况,采用ROC标准用于预测结果评估,具体指标包括:召回率(True Positive Rate,TPR),为正类样本中被正确预测的占比;f1测度(f1-score,f1),为召回率和准确率(被预测为正类样本中实为正类的占比)的调和平均;AUC值(Area Under Roc Curve,AUC),等价于分类器对正类中随机样本评分高于反类中随机样本的概率。
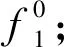
2 研究区滑坡概况及数据集
2.1 研究区滑坡地质环境
本文选取的三峡库区内26个“阶跃式”岸坡(图2),均为堆积层-基岩组合形式,以侏罗系地层的砂岩、泥岩为主,地层岩性具有易风化、遇水软化等特点,剪出口相近,前缘位于175 m库水位以下。库区水位为145~175 m,涨落高差达30 m,相应的库岸地灾体水位变化也基本如此。该区属亚热带季风性湿润气候,全年的气候特征为湿度大、降雨充沛,年均平均降雨量达到996.7~1 309.9 mm。夏季长而热、多暴雨,秋多阴雨,冬暖、春旱。丰富的水资源为“阶跃式”滑坡灾害提供了外部条件,使得岩土体强度降低,坡体自重变化,产生动水压力和浮托力,使得坡体稳定性急剧下降。
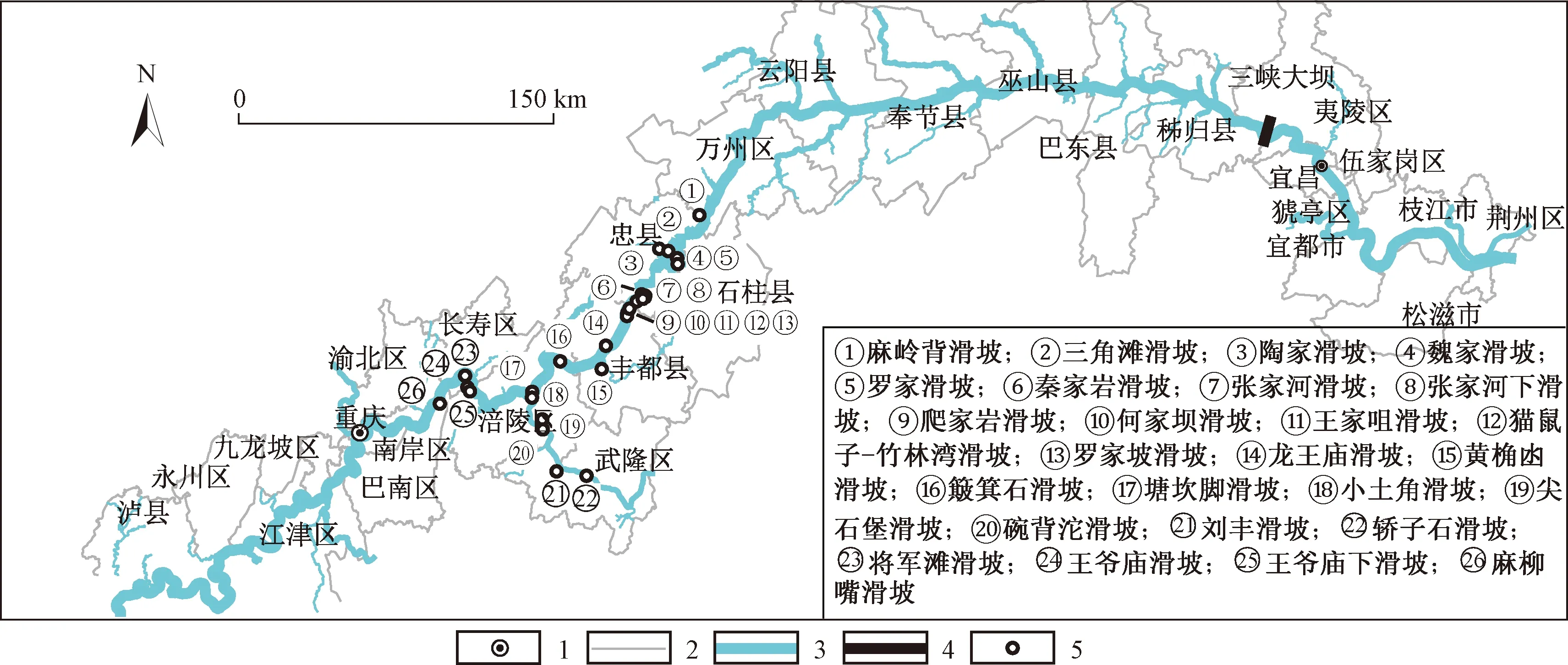
图2 研究区滑坡分布Fig.2 Distribution of landslides in the study area1—行政中心;2—区县界;3—库区;4—三峡大坝;5—滑坡。
2.2 数据归一化处理
滑坡的地质环境因子分为内部和外部[17]。内部因子数据包括地形地貌、地层岩性和地质构造[18]等,基本趋于稳定,由现场勘查获取;外部因子数据包括降雨和库水[19]等,它随时间活跃变化,由监测点实时监控。因子选取尽量体现真实数据的差异性,但由于调研数据难以包含所有地质情况,部分因子及分级类别不够齐全。汇编数据以月为周期,并考虑了降雨和库水的滞后效应[20-21],最终选取可获取的、较为完整的26个地质环境因子(表1)。为了验证模型可行性、实用性,随机抽取出王爷庙滑坡作为预测集校核模型,另25个滑坡构成因子计算、机器学习及测试的总数据集。
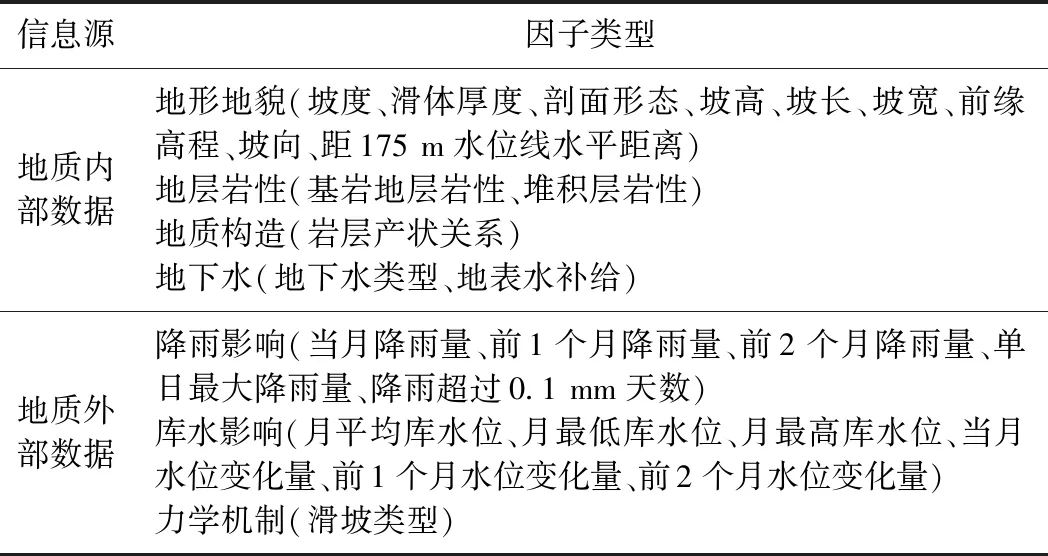
表1 26个滑坡地质环境因子Table 1 26 Geological environment factors of landslides
数据的归一化是算法实现的前提。由于数据平衡化是基于广义欧式距离实现的,针对离散型因子,先采用各因子相应的二级因子突变频率比[22]进行数据连续化,作为衡量因子的量化指标:

(2)
式中,ni,j——各类二级因子突变样本;
mi,j——该二级因子集合,其中i为环境因子序号,j为所在因子分类的二级因子序号。
再将所有连续型在内的因子离差标准化,映射至[0,1]区间消除量纲影响,作为自变量供模型使用,离散型因子分级与连续化结果如表2至表9所示。

表2 滑坡类型因子分级与连续化Table 2 Classification and continuous of landslide type

表3 剖面形态因子分级与连续化Table 3 Classification and continuous of profile morphology

表4 基岩地层岩性因子分级与连续化Table 4 Classification and continuous of bedrock lithological

表5 堆积层岩性因子分级与连续化Table 5 Classification and continuous of accumulative formation lithological
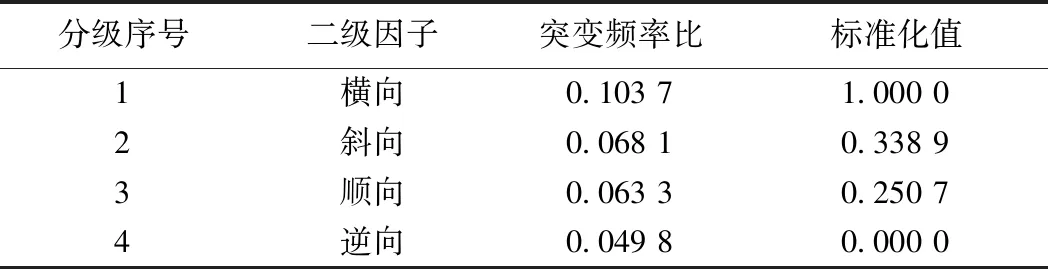
表6 岩层产状关系因子分级与连续化Table 6 Classification and continuous of rock stratum occurrence
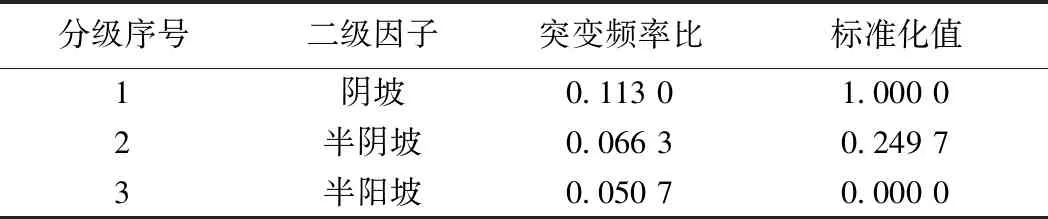
表7 坡向因子分级与连续化Table 7 Classification and continuous of aspect

表8 地下水类型因子分级与连续化Table 8 Classification and continuous of groundwater type

表9 地下水补给因子分级与连续化Table 9 Classification and continuous of groundwater recharge
滑坡地表水平位移监测数据作为突变依据,结合“阶跃式”滑坡曲线连续突变的特征,以统计学中离群值检验的四分位上界[23]对各监测点月位移量进行划分,用作数据集的因变量,其中突变记作1、稳定记作0。将突变频次与降雨量、库水位比较,发现三者具有较强的相关性。图3为2006年6月至2018年8月期间,研究区“阶跃式”滑坡总突变频次与月平均降雨量、月平均库水位的关系。
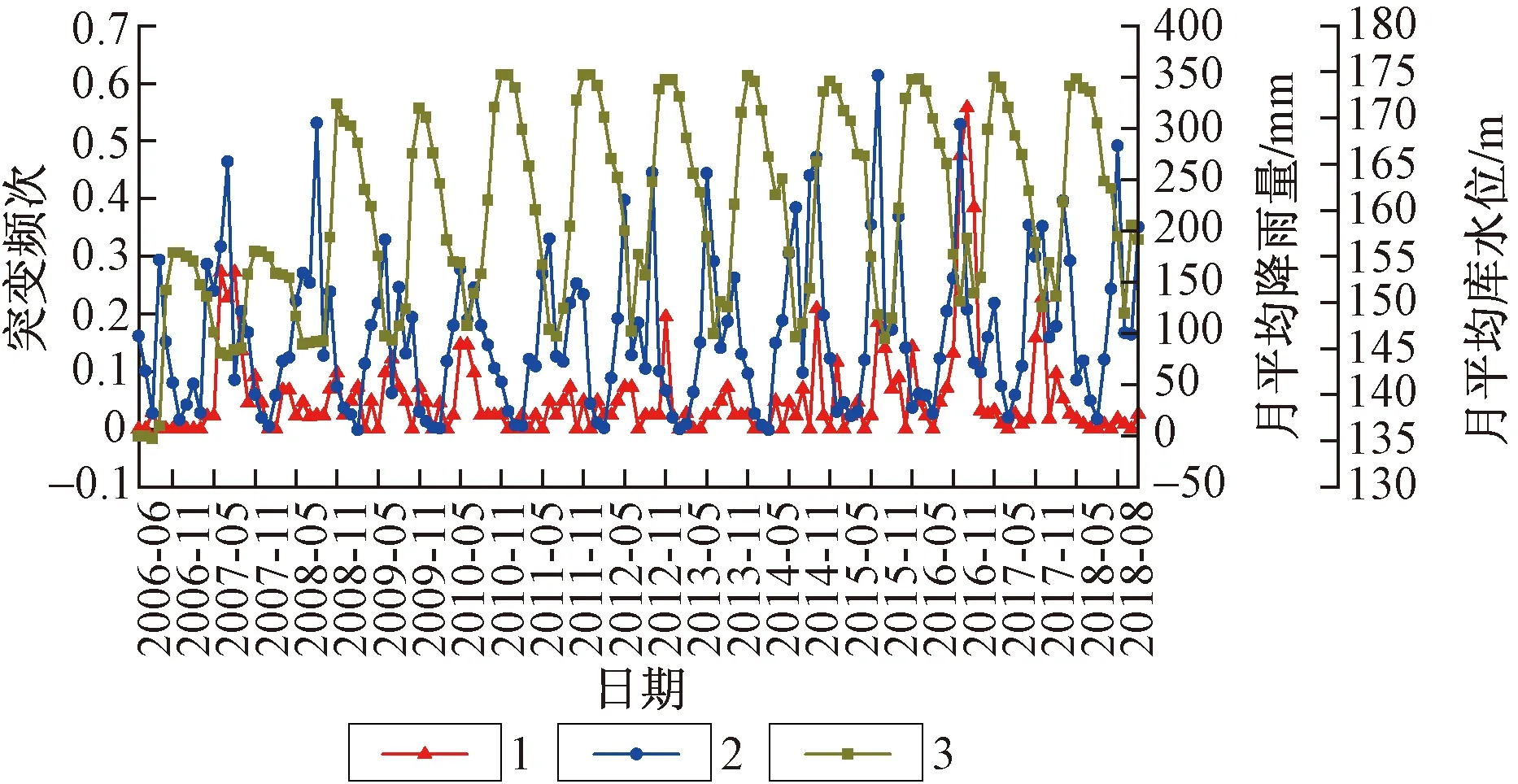
图3 “阶跃式”滑坡的总突变频次与月平均降雨量、月平均库水位的相关性曲线Fig.3 The correlation curve between the catastrophe frequency of step-like landslides and monthly average rainfall, monthly average reservoir water level1—突变频次;2—月平均降雨量;3—月平均库水位。
2.3 “阶跃式”滑坡数据集
建立所有变量总和的“阶跃式”滑坡数据库,总数据集按3∶1划分为训练集和测试集,其中训练集根据不同过采样比率参数合成新的样本集用于集成树训练使用,测试集不参与模型的训练过程用于评估训练模型对于新数据的泛化表现。如表10所示,数据集中样本数目分布严重不平衡,直接用于传统分类算法必将导致训练结果更倾向于稳定类,对突变类学习效率降低。因此,在数据层面对目标变量进行平衡优化是提升突变信息学习效率的突破点。

表10 “阶跃式”滑坡数据集Table 10 The data set of step-like landslide
3 模型应用与分析
3.1 模型测试结果比较
模型测试结果比较分为三步:(1)采用初始训练集分别训练传统单分类算法(KNN、SVM、LR、NB、CART)和集成树算法(RF、GBDT),并进行测试结果评估;(2)采用比率参数为1的平衡化训练集对上述方法进行训练并测试评估;(3)通过比率参数搜索构造两种最佳平衡状态下的平衡集成树(Borsmote1-RF和Borsmote1-GBDT)模型。
(1)传统单分类算法与集成树算法的测试结果比较
实验对所选模型分别进行了泛化调参,用没有参与训练的测试集进行结果评估(表11)。
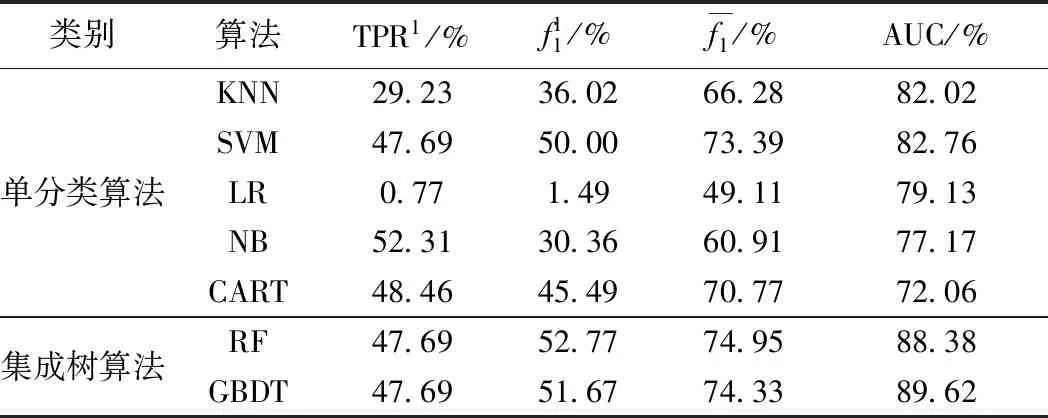
表11 初始训练集对应的不同算法测试结果Table 11 Different algorithm test performances corresponding to the raw training set
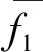
(2)比率参数为1的平衡优化算法比较
比例参数表示过采样后突变类数量与稳定类之比,采用比率参数为1对测试集进行平衡操作,此时突变类与稳定类数量相等,以此分别对(1)中的所有方法进行优化。训练过程同样采取了泛化措施,优化后的训练模型用于测试集预测结果评估(表12)。
表12 比率参数为1的平衡优化算法测试结果Table 12 Balanced optimization algorithm test performances at a ratio of one

(3)构造最佳平衡状态下的平衡集成树模型
合成突变类过程中,比率参数使合成突变类数线性增加,决定了数据平衡的程度,直接影响分类器性能。之前的实验已经证明比率值为1时平衡优化的集成树算法精度最高,通过调节比率值可以进一步挖掘训练模型的最佳平衡状态。每种组合的平衡优化集成树模型同样经过泛化训练获得,整个平衡过程的结果如图4所示。

图和AUC预测精度随测试集比率参数变化曲线图Fig.4 The values of and AUC vary with ratio parameters1—RF;2—GBDT;3—Borsmote1-RF;4—Borsmote1-GBDT。
和AUC值整体上先快速上升然后缓慢下降,中间有较大波动,三者趋势比较相似。Borsmote1-RF模型在比率为0.5时,测试精度最高,而Borsmote1-GBDT模型当比率为0.7时效果最佳,可以认为这两点为两种模型的最佳平衡状态。当比率继续增大时,模型测试结果精度下降,这是因为合成少数类样本并非真实样本,过多亦会造成数据集质量降低,平衡化程度并非越平均越好。

表13 最佳平衡状态下的平衡集成树测试结果Table13 Test results of balanced decision tree ensemble under optimal equilibrium
3.2 核心因子提取
因子与突变的关联是非线性和离散的,而采用相关性系数分析相关性前提是线性情况,因此采用以往常用方法提取因子特征具有局限性。平衡集成树模型对于“阶跃式”滑坡突变预测的精度得到了有效提升,表明模型在数据平衡过程中经过边界增强、噪音消减更易于捕捉到了突变的核心相关因子,可以认为基于平衡集成树信息增益率给出的因子特征重要性比集成树更具有参考与实用价值。按照borsmote1-RF(0.5比率)模型计算的26个地质环境因子特征重要性进行降序排列,图5得出集成树改进前后该研究区的因子重要性。
由图5可知,外部因子较内部因子影响更为显著,其中降雨、库水位和内部因子三者的比重和约为27.85%、52.43%和21.00%,该比例受因素数量影响,但可作为定性参考分析。可见,库水位为三峡库区“阶跃式”滑坡的主导因素,且水位下降导致失稳的作用强于水位上涨;降雨为主要因素,其中前1个月降雨量和单日最大降雨量影响较大。
图6为bormote1(0.5比率)情况下,主要因子所对应的平衡化突变类、稳定类和初始突变类三者的分布特征。经过平衡化的数据集降低了树节点划分突变的不纯度值,且各因子的分布特征均能够得到较好的可解释性。如图6(a)、图6(b)、图6(d)和图6(e)所示,突变集中发生在月最低库水位[144 m,154 m]、月最高库水位[153 m,162 m]和月平均库水位[144 m,158 m]段,当月水位变化量则多发于[-12 m,-8 m]和[4 m,10 m]两个区间段(突变发生的[-4 m,0 m]区段是稳定类的集中区段,因此突变频率相对较低),表明库水位的骤升和骤降均是诱发“阶跃式”滑坡失稳的重要因素;如图6(c)、图6(d)所示,单日最大降雨量为40 mm和前1个月降雨量为125 mm左右,是“阶跃式”滑坡突变启动的一个转折点,且均与突变呈正相关。
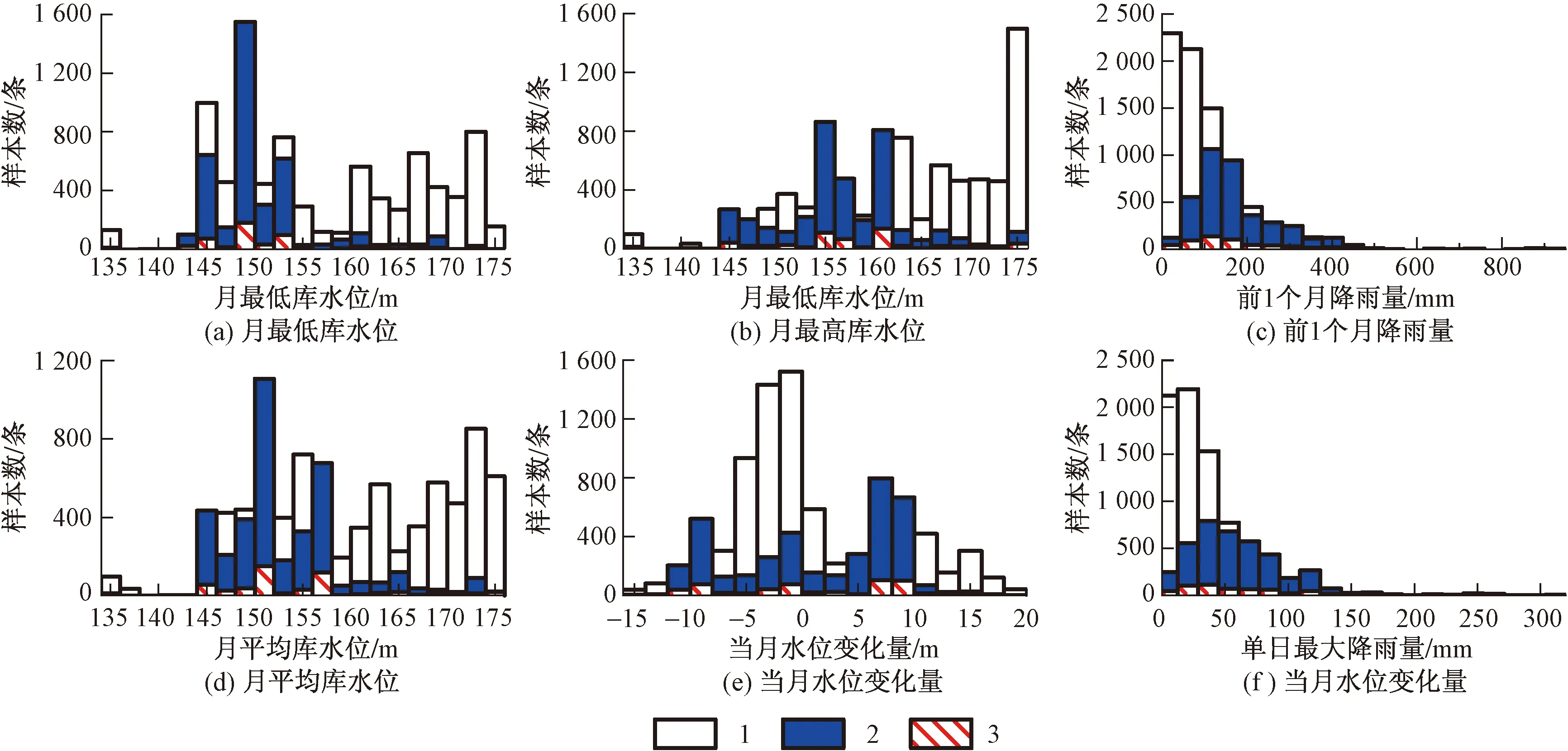
图6 主要因子对应的稳定类、平衡化突变类和初始突变类三者的分布特征Fig.6 Distribution characteristics of balanced mutants, stable classes and initial mutations corresponding to major factors1—稳定类;2—平衡化突变类;3—初始突变类。
3.3 王爷庙滑坡案例分析
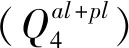
历年来,滑坡受雨季降水(图7)和库水波动(图8)影响,滑体沿基岩接触面向下滑动,前缘经江水浸泡、冲刷和淘蚀而失去支撑,变形加剧,处于欠稳定状态。其中中部WYM05号监测点累计地表水平位移达5 681.6 mm,该点自2007年雨季开始变形,时空曲线为“阶跃式”发展,历经多个突变时段(主要为2007年5~8月,2008年9月,2009年2月、5~11月,2010年4~6月,2011年5月,2012年5~7月,2013年6月,2014年5~12月,2015年6~7月,2016年4~10月),位移方向81°~85°同主滑方向基本一致。
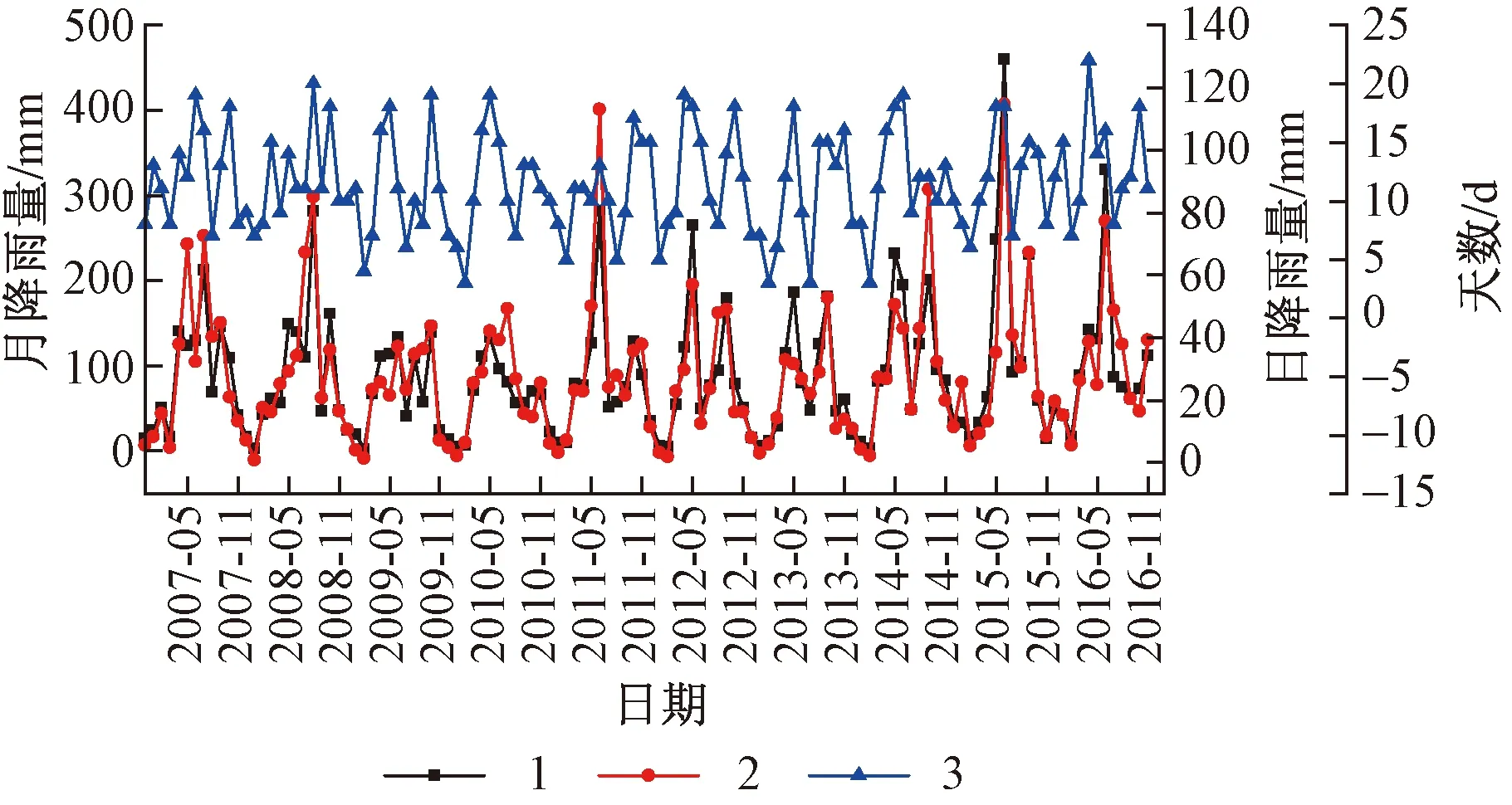
图7 王爷庙滑坡降雨监测曲线Fig.7 Monitoring curves for precipitation of Wangyemiao landslide1—当月降雨量;2—单日最大降雨量;3—降雨超过0.1 mm天数。
图8 王爷庙滑坡库水监测曲线Fig.8 Monitoring curves for reservoir water level of Wangyemiao landslide1—月平均库水位;2—当月水位变化量。

图9 WYM05号监测点累计位移曲线和预测结果Fig.9 Accumulated displacement curves and prediction results of monitoring point WYM051—预测为稳定类;2—预测为突变类。
4 结论和展望
本文提出了平衡集成树模型对“阶跃式”滑坡突变预测和特征提取进行了研究分析,得出如下结论:
(1)模型考虑了滑坡监测数据处理中的不平衡问题,通过合成边界突变类,使模型能够有效获取“阶跃式”滑坡突变与复杂地质环境因子间的关联。与传统算法相比较,该算法实现了海量监测数据下的有效泛化和准确分析,解决了传统突变预测方法效率低的问题;
(2)该方法能够较好反映研究区内不同时段不同条件下因子对“阶跃式”滑坡失稳的影响作用。本文探讨了以月为周期的预测分析,并进行因子特征重要性比较,研究方法及所得规律可为相关工程和研究提供重要的参考价值;
(3)通过测试集和预测集结果评价,模型性能达到了实际预报要求,验证了平衡集成树模型应用于“阶跃式”滑坡风险评估与机理研究的可行性。同时,处理和解决滑坡灾害数据分析中的数据不平衡问题,是实现智能滑坡灾害分析与大数据预警的必然趋势。
