一种改进的模块化多电平换流器模型预测控制策略

龚向阳，蔡振华，谢宇哲，叶夏明，邱 云，王 宁

(1.国网浙江省电力公司宁波供电公司，浙江 宁波 315000；2.燕山大学 电气工程学院，河北 秦皇岛 066004)

0 引言

模块化多电平换流器(Modular Multilevel Converter，MMC)的结构如图1所示，由六桥臂构成，每个桥臂由数百个子模块串联组成。半桥型MMC的子模块由两个绝缘栅双极型晶体管(IGBT)串联后和一个储能电容并联构成，通过控制两个IGBT的通断可以控制子模块在桥臂中的插入与切除状态，通过控制每一相上下桥臂的插入子模块个数可以控制该相交流侧输出电压电平，子模块个数越多，输出电平数越多，可以越好地逼近正弦波。由于其特殊的结构，MMC换流器具有低谐波失真、低开关频率、低开关损耗、效率高、易于模块化设计的特点，因而在高压直流输电领域得到了日益广泛的应用。

MMC的控制目标主要体现为跟踪交流侧输出电流、降低桥臂子模块能量波动和抑制相间环流。已经有很多研究提出了MMC调制方法与控制策略，文献[1]对多种半桥拓扑结构子模块的MMC载波脉宽调制策略进行了比较分析。文献[2]提出了一种灵活逼近调制策略，实现模块开关频率降低的目的。文献[3]中提出一种通过交流输出电流与直流电压来估计桥臂存储能量进而控制桥臂能量平衡与抑制环流的开环控制方法。文献[4]提出了基于电容电压纹波分析的电压均衡控制器设计。文献[5]分析了电容电压均衡控制对子模块开关频率的影响，推导了子模块电容不平衡电压与子模块开关频率之间的关系式。文献[6]提出一种对子模块虚拟电容电压进行排序，进而降低子模块开关频率的控制方法，并分析了电容电压均衡控制对子模块开关频率的影响，推导了子模块电容不平衡电压与子模块开关频率之间的关系式。

图1 三相MMC结构图

Fig.1 Structure of three-phase MMC

以上模型预测控制方法虽然能够在MMC中应用，但尚存在不足。若不以每一个子模块的开关状态作为控制操作选项，则系统除了MPC模块还需要单独的电容电压均衡控制模块；若以每一个子模块的开关状态作为控制操作选项，则不能应用于具有大量子模块的MMC系统。本文提出一种基于电容电压桶排序的双层模型预测控制方法。首先对电容电压进行桶排序，子模块根据电压顺序依次进行分组；以每一组的开关状态作为控制选项进行模型预测控制，得到需要插入的组；再以每一个子模块的开关状态为控制选项，对组内子模块进行模型预测控制。该方法不需单独电容电压均衡控制模块，降低了电容电压排序的复杂度，可以保证每一时刻投入的子模块都是电容电压最小或最大的子模块；通过非穷举方法达到与穷举相同的效果，寻优次数大大减少。应用PSCAD/EMTDC搭建101电平MMC-HVDC系统对本文方法进行了仿真验证。

1 MMC数学模型

以三相MMC中的一相为例进行分析，如图2所示。

图2 MMC单相结构图

Fig.2 Single-phase circuit of the MMC system

根据基尔霍夫电压定律可知

(1)

式中，uTj、uDj分别为j相上下桥臂投入子模块的电压，uACj为j相交流侧输出电压，LARM、RARM分别为桥臂上的电感与电阻，LLINE、RLINE分别为交流侧输出线路上的电感与电阻，iACj为j相交流输出电流，iTj、iDj分别为上下桥臂电流。

所以由式(1)可得到

iACj=iTj-iDj，

(2)

(3)

其中

(4)

上下桥臂的电流满足如下关系

(5)

式中，iDIFFj为j相内部差动流，满足

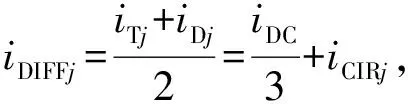
(6)

式中，iCIRj为相间环流。

j相和直流侧构成的环路根据基尔霍夫定律可得

uDC=uTj+uDj+RARMiTj+

(7)

由式(5)、(7)可得

(8)

综上所述，MMC系统数学模型可以表示为

(9)

根据式(9)，使用欧拉法得出系统离散时间模型为

(10)

2 电容电压桶排序

传统的模型预测控制得到上下桥臂的最佳投入子模块个数搭配后，还需要单独的控制模块使用基于电容电压排序的算法进一部确定哪些子模块需要投入[17]。高压直流输电中单臂子模块通常有数百个子模块，普通排序算法时间复杂度较高，在实际应用中对硬件要求较高[18]。针对以上问题本文使用桶排序的方法对电容电压进行排序，电压排序后的子模块被均分到各组中，进而进行后续的模型预测控制。

电容电压均分桶排序流程如图3所示，设单臂有n个子模块，设桶排序中桶的个数为a个，这也是桶排序之后子模块分组的个数,每组包含b个子模块。n=a×b，a、b均为正整数。采集到桥臂各个子模电压之后将进行以下步骤：

1)找出子模块电容电压的最大值与最小值，在这两个最值之间进行等分得到a个电压区间，即得到a个桶；

2)将所有的电压值分配到相应的各个桶中，分别在桶内进行电容电压排序，排序时所有电压都应保留相应的子模块标号；

3)由于电容电压不会均等地分布在步骤1)中划分的电压区间中，因而电压排序后的子模块还需按顺序均等地分配到a组中，每组包含b个子模块。

假设初始电压数据均匀地分布在每一个桶中，则该排序方法的时间复杂度为O(n+n·(logn-loga))[19]，即使不均匀分布，其排序的时间复杂度也与之接近。相对于时间复杂度为O(n2)的冒泡排序方法[20]，该方法大大减少了控制系统的计算任务。经过以上流程，桥臂上n个子模块被按电压大小顺序均分为a组，每组中的b个子模块也按照电压大小顺序排列，每一个电压值保留对应的子模块编号。

图3 电容电压桶排序流程图

Fig.3 Flow chart of capacitor voltage bucket sorting

3 双层模型预测控制

将桶排序处理结果中每一个包含b个子模块的组看作一个等效子模块，设子模块中电容为C，等效子模块电容为CEQ=C/b，等效子模块电压为对应组内电容电压之和。

设j相上下桥臂各个等效子模块电压表示为

(11)

设采样时间为TS，下一采样时刻上下桥臂各个等效子模块电容电压分别为

uEQ_Tj(i)(t+Ts)=

(12)

uEQ_Dj(i)(t+TS)=

(13)

下一采样时刻桥臂子模块的总能量为

(14)

桥臂能量参考值为

(15)

针对桥臂能量这一被控变量，代价函数设计为

J1=|WREF_Tj-WEQ_Tj(t+Ts)|+

|WREF_Dj-WEQ_Dj(t+TS)|，

(16)

对于另外两个被控变量，交流侧电流和相间环流的代价函数设计如下：

J2=|iACj(t+TS)-iREF_ACj|，

(17)

J3=|iDIFFj(t+TS)-iREF_DIFFj|，

(18)

式中，iACj(t+TS)和iDIFFj(t+TS)根据式(10)计算，为了抑制相间环流，j相内部差动电流参考值iREF_DIFFj设置为iDC/3，交流侧电流参考值iREF_ACj根据无功和有功功率或者直流电压设定值来设定。

总代价函数设置为

J=α1J1+α2J2+α3J3，

(19)

其中，α1、α2、α3分别为3个代价函数的权重。

按照桥臂电流为正，投入电容电压最低的若干个等效子模块，桥臂电压为负投入电容电压最高的若干个等效子模块的原则，通过式(12)、(13)计算所有可选控制选项下的上下桥臂预测等效子模块电压值，计算各个代价函数值，进而得出使代价函数最小的上下桥臂等效子模块开关状态，完成第一次模型预测控制。

第一次模型预测控制可得到需要投入多少个等效子模块，相当于得到了需要投入子模块个数的大致范围，下一步将进行第二次模型预测控制得出子模块的开关状态。

设第一次MPC得出上下桥臂分别需要投入p和q个等效子模块，且满足p+q=α,0≤p，q≤a,第二次MPC的使用将在第一次MPC得到的最佳子模块投入个数范围内进行寻优。上桥臂的寻优区间根据式(20)确定：

(20)

由于上下桥臂投入子模块个数之和固定为n，所以下桥臂寻优区间有相同的确定规则。

设j相上下桥臂各个子模块电压表示为

(21)

按照寻优区间内的投入子模块个数依次计算各种控制选项下的下一时刻各个子模块电容电压分别为

uTj(i)(t+TS)=

(22)

uDj(i)(t+TS)=

(23)

下一时刻桥臂能量计算如下

(24)

下一时刻桥臂差动电流和交流侧电流根据式(10)计算，三个被控变量的参考值和代价函数计算与第一次使用MPC相同。满足使第二次MPC代价函数最小的控制选项即为最佳控制选项。所提出的基于桶排序的分层模型预测控制方法原理如图4所示。

图4 基于桶排序的分层模型预测控制方法原理图

Fig.4 Schematic of hierarchical MPC method based on bucket sorting

所提方法的流程如图5所示，首先对所有子模块电容电压进行桶排序，得到按大小顺序排列的子模块和等效子模块。对等效子模块进行第一次模型预测控制，得要需要投入的等效子模块的最佳控制选项，根据最佳等效子模块的控制选项确定的范围，进行第二模型预测控制得到子模块的最佳控制选项。

图5 基于桶排序的分层模型预测控制方法流程图

Fig.5 Flow chart of hierarchical MPC method based on bucket sorting

所提出方法的寻优次数由等效子模块的个数和组内子模块个数决定，第一次模型预测控制中对a+1个控制选项进行了代价函数计算，第二次模型预测控制要对b+1个或者2b+1个控制选项的代价函数进行计算，寻优总次数为a+b+2或a+2b+2。相对于传统FCS-MPC方法和单次模型预测控制的方法相比，在不同桥臂子模块个数情况下需要寻优的次数对比如表1所示。从表中可以看出所提方法将大大减少MPC应用于MMC系统时的寻优次数，进而大大减少计算任务，提高计算速度。

表1 各种MPC方法控制选项数对比

Tab.1 Comparison of control options for various MPC methods

桥臂子模块数FCS-MPCOnce MPC本文MPC100C10020010132(分10组)200C20040020142(分20组)300C30060030152(分20组)400C40080040162(分20组)

4 仿真验证

为验证提出方法的控制效果，在PSCAD/EMTDC下搭建了双端背靠背101电平的MMC-HVDC系统进行稳态与暂态试验验证，双端系统的简要控制原理如图6所示，系统的主要参数见表2，一端采用有功功率和无功功率控制，一端采用直流电压与无功功率控制。基于模拟结果的变化来选择合适的代价函数权重，α1、α2、α3分别设置为0.005、1、1。

图6 双端背靠背MMC系统MPC控制原理图

Fig.6 Schematic of the proposed MPC applied in the back-to-back MMC-HVDC

表2 MMC-HVDC仿真系统相关参数

Tab.2 Parameters of the MMC-HVDC simulation system

参 数数值桥臂子模块个数N100交流频率f/Hz50时间尺度TS/μs50分组个数a10交流侧线电压UAC/kV380(RMS)直流侧额定电压UDC/kV400有功功率P/MW200无功功率Q/Mvar0变压比/(kV/kV)380/220交流侧电阻RLINE/Ω1交流侧电感LLINE/mH20桥臂电感LARM/mH25子模块电容C/mF10

本文以图6中MMC1系统的各项参数展示控制效果，稳态仿真实验结果如图7～12所示。图7显示第一层MPC输出的A相上桥臂最佳等效子模块插入个数和第二层MPC输出的A相上桥臂最佳子模块插入个数，输出曲线稳定，曲线走势一致。图8显示A相上桥臂的100个子模块中前10个子模块的电压，可见子模块电压在4 kV上下约±1.5%范围内波动，子模块电压控制效果良好。图9显示了6个桥臂的电压变动，由于直流侧电压设置为400 kV，所以桥臂电压控制良好。图10显示了桥臂上的100个子模块电容电压之和在400 kV附近约±1.5%范围内波动，表明桥臂能量均衡控制效果良好。图11显示交流侧电流的设定值与实际值曲线，实际值与参考值很好的吻合，交流侧电流控制效果良好。图12显示相间环流值，相对于交流侧电流的复幅值0.2 kA，相间环流得到了很好的抑制。以上各变量显示系统的稳态控制效果良好。

图7 双层MPC输出的投入等效子模块和子模块个数

Fig.7 The number of inserted equivalent SMs and SMs of double-layer MPC output

图8 子模块电容电压

Fig.8 Capacitor voltage of SMs

图9 桥臂电压

Fig.9 Voltage of the arms

图10 桥臂子模块电压之和

Fig.10 The voltage sum of the SMs

图11 交流侧电流参考值与实际值

Fig.11 Current reference and actual value of the AC side

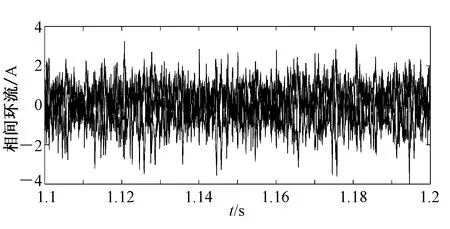
图12 相间环流

Fig.12 Circulating current

为测试系统的暂态控制效果，在3 s时系统有功功率的设定值从200 MVA减少至150 MVA。各变量的控制效果如图13～15所示。图13显示子模块电压波动情况，在不到0.2 s时间内，子模块电容电压波动恢复平稳。桥臂子模块电压之和动态响应如图14所示，与子模块电压动态响应波动趋势一致。交流侧电流动态响应如图15所示，显示其也有良好的暂态控制效果。由于系统功率设定值下降，所以各个动态响应曲线显示在新的稳态各变量波动范围或幅值减小。本文所提方法计算时间短，可满足实时控制要求。

图13 子模块电容电压动态相应曲线

Fig.13 Dynamic corresponding curve of the capacitor voltage

图14 桥臂子模块电压之和动态响应曲线

Fig.14 Dynamic corresponding curve of the voltage sum

图15 交流侧电流动态响应曲线

Fig.15 Dynamic corresponding curve of the AC-side current

5 结论

本文提出了一种基于电容电压桶排序的MMC分层模型预测控制方法，对子模块电压进行桶排序，电压排序后的子模块等分为若干组，每一个组看作一个等效子模块。设计了MMC离散时间数学模型，设计了考虑交流侧电流，相间环流和桥臂能量三个变量的代价函数。通过第一层MPC得到需要投入的等效子模块之后，使用第二层MPC确定需要投入的子模块。所提出方法通过减小电容电压排序的时间复杂度和减少MPC中最佳控制选项的寻优次数，大大减少了MPC应用于MMC系统时的计算任务，减少实际应用中对硬件设计的要求。所提出方法在PSCAD/EMTDC下搭建的101电平的MMC-HVDC系统中进行了测试，并验证了所提方法的稳态与暂态控制性能。