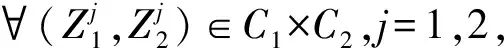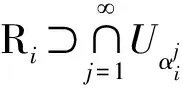n方体连续自映射混沌集合的Hausdorff维数
2019-11-09吴华明
吴华明
(岭南师范学院 数学与统计学院, 广东 湛江 524048)
Ivan[1]在1988年用Lebesgue测度作为标准来研究线段自映射混沌集合的大小,得到了C0(I)中存在一个剩余集R,使得对于每一个映射f∈R,对于f而言的每一个Li-Yorke混沌集合[2]的Lebesgue测度为0.顾荣宝[3]用Hausdorff维数作为度量的标准来研究线段自映射混沌集合的大小,得到了C0(I)中也存在一个剩余集R,使得对于每一个映射f∈R,若C⊂I对于每一个f而言是Li-Yorke混沌的,则C的Hausdorff维数dimH(C)=0.文献[4]将结果推广到I2上有类似的结论.本文将文献[4]的结果推广到高维的情形.
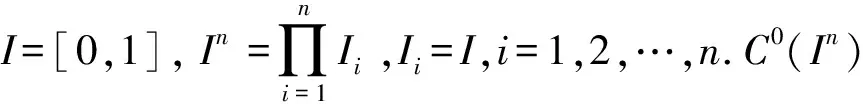
本文主要结果是:存在剩余集R ⊂C0(In),使得对每个f∈R,若C⊂In对f而言是Li-Yorke混沌的,则C的Hausdorff维数dimH(C)≤n-1,并且C是第一范畴集.
该结果对高维笛卡尔积的情形也成立,即在C0(Ini,Ini)中存在一个剩余集Ri,使得对于每个fi∈Ri,i=1,2,若集合Ci⊂Ini对于fi而言是Li-Yorke混沌的,则dimH(C1×C2)≤n-1,且C1×C2是第一范畴集.
1 预备知识
1.1 方体
定义 1设m是任一正整数,
A={(t1,…,tm)|ri≤ti≤si, i=1,2,…,m}⊂Rm
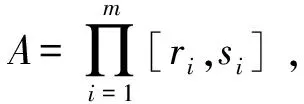
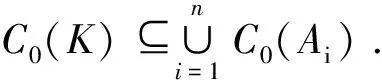
显然Ai均是K的闭子集,根据黏合引理,若有连续映射族fi:Ai→Rl,使任意2个在公共面上的取值相同,则有连续映射:f:K→Rl,使f|Ai=fi.
1.2 方体的面
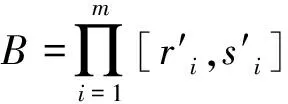
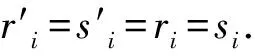
2) 当ri 易见,若BA,则: 1)B⊂A, 2) 0≤ dim B≤dimA, 在方体A的面中,有2个特殊的面A0和A1,分别称为方体A的前面和后面,其中 当rm=sm时,A0=A1=A;当rm dimA0=dimA1=dimA-1. 显然C0(A)=C0(A0)∪C0(A1). 对∀x=(t1,…,tm)∈A,称点 x0=(t1,…,tm-1,rm)∈A0, x1=(t1,…,tm-1,sm)∈A1 分别为x的前影和后影,则x=(1-t)x0+tx1,其中t=(tm-rm)/(sm-rm),若rm 1.3 典型同构设k 设A为Rm中的方体,显然P(A0)=p(A1)=p(A)是Rm中的方体,且p|A0和p|A1都是线性保内积的同胚.而且p|C0(A0):C0(A0)→C0(p(A))和p|C0(A1):C0(A1)→C0(p(A))是一一对应的,称p|A0和p|A1为典型同构.若BA,则p(B)p(A). 1.4 方体上的多重线性扩充任给g0:C0(A)→Rl,对m归纳地定义g:A→Rl如下:当m=1时,A=[r1,s1],若r1=s1,则A为单点,令g=g0即可;若r1 g(t1)=(1-t)g0(r1)+tg(s1),t1∈A, 其中t=(t1-r1)/(s1-r1),此时,称g为g0的多重线性扩充. 上述的g有性质: (Ⅰ)g|C0(A)=g0; (Ⅱ)g连续; (Ⅲ)g(A)⊂[g0(C0(A))],其中[g0(C0(A))]为g0(C0(A))的凸包; (Ⅳ) 设BA,则g|B是g0|C0(B)的多重线性扩充. 设当m=k-1时,满足上列性质(Ⅰ)~(Ⅳ)的多重线性扩充g已定义,对m=k时定义映射g,且称满足性质(Ⅰ)~(Ⅳ)的g为g0的多重线性扩充. 给定方体A⊂Rl,g0:C0(A)→Rl,则在Rk-1中的方体p(A)上,有2个函数: g(x)=(1-t)g′(p(x))+tg″(p(x)), 其中x=(t1,…,tk),t=(tk-rk)/(sk-rk),若rk 设K为Rm中的复合方体,g0:C0(K)→Rl,则g0限制在每个方体上都有一个多重线性扩充,由性质(Ⅳ),这些扩充在公共面上取值一致,故有连续映射g:K→Rl,使得它在顶点上与g0一致,在每个方体上的限制均为多重线性扩充,且g对于每个方体均满足性质(Ⅲ).易见g也满足性质(Ⅰ)和(Ⅱ). 定义 3设K为Rm中的复合方体,g0:C0(K)→Rl,则称上述g为g0在K上的多重线性扩充. 为方便起见,先引入一些记号.Z+表示正整数集,m∈Z+,M=2m,η=2-2m2,ai=i/M,i=0,1,…,M;ci=(ai-1+ai)/2,i=1,2,…,M. Eim=[ai-1+η,ai-η], Fim=[ci-η,ci+η],i=1,2,…,M; Him=[ai-η,ai+η],i=1,2,…,M-1; H0m=[0,η],HMm=[1-η,1]; Cm={(ci1,ci2,…,cin)|i1,i2,…,in∈{1,2,…,M}}; Dm={a0,a0+η,a1-η,a1+η,…,aM-η,aM}; Qm={(z1,z2,…,zn)|zi1,…,zik∈{0,1},zik+1,…,zin∈Dm-{0,1},i1,i2,…,in为1,2,…,n的一个排列,k=1,2,…,n}. 引理 1R是C0(In)的剩余集. 对每个m∈Z+,Am显然是C0(In)中的开集,事实上Am是C0(In)的紧致开拓扑的基元素. (1) 为一复合方体. 下面定义g0:C0(k)→In如下: (b) 对z=(z1,z2,…,zn)∈Qm,g0(z)为Cm中距离f(z1,z2,…,zn)最近的点(若这样的点不唯一,可任取定一个),则存在g0在复合方体K上的多重线性扩充g,从而g(Em)⊂(Fm)0,即g∈Am. 往证ρ(f,g)<ε.对∀(ci1,ci2,…,cin)∈Cm, 事实上有 |f(ci1,ci2,…,cin)-g(ci1,ci2,…,cin)|≤ 对于 ∀z∈[ai1-1,ai1]×[ai2-1,ai2]×…×[ain-1,ain], 由(1)式有 |f(z)-f(ci1,ci2,…,cin)|<ε/5. (3) 事实上,由于[aij-1,aij]的长度不超过2-m,故 由(1)式有|f(z)-f(ci1,ci2,…,cin)|<ε/5,对∀z∈Em. 由(2)和(3)式有 |f(z)-g(z)|<2ε/5. (4) 事实上 |f(z)-g(z)|≤|f(z)-f(ci1,…,cin)|+ |f(ci1,…,cin)-g(ci1,…,cin)|+ |g(ci1,…,cin)-g(z)|<2ε/5. 若(ci1,…,cin)∈Cm∪Qm,则 |f(ci1,…,cin)-f(ch1,…,chn)|<ε/5, hk=ik或ik+1, k=1,2,…,n. (5) 事实上 |(ci1,…,cin)-(ch1,…,chn)|≤ 由(1)式有 |f(ci1,…,cin)-f(ch1,…,chn)|<ε/5. 由(2)式和(a)、(b)有 |g(ci1,…,cin)-g(ch1,…,chn)|<3ε/5. (6) 事实上 |g(ci1,…,cin)-g(ch1,…,chn)|= |g(ci1,…,cin)-f(ci1,…,cin)+ f(ci1,…,cin)-f(ch1,…,chn)+ f(ch1,…,chn)-g(ch1,…,chn)|≤ |g(ci1,…,cin)-f(ci1,…,cin)|+ |f(ci1,…,cin)-f(ch1,…,chn)|+ |f(ch1,…,chn)-g(ch1,…,chn)|<3ε/5. 且至少存在一个1≤t≤n,使 取(ci1,…,cin)为Cm∪Qm与z点距离最小的点(若这样的点不唯一,可任取一个).若 |f(z)-g(z)|≤ |f(z)-f(ci1,…,cin)|+|f(ci1,…,cin)- g(ci1,…,cin)|+|g(ci1,…,cin)-g(z)|≤ ε/5+ε/5+|g(ci1,…,cin)-g(ci1,…,cin)|<ε. 因此,Bn是C0(In)的稠密开集,故R是C0(In)的剩余集. 引理 2对于任意f∈R,若集合C⊂In对于映射f而言是Li-Yorke混沌的,则存在严格递增的正整数序列{nk},使得 (7) 证明设f∈R,则存在严格递增的正整数序列{nj},使得对每个j∈N,f∈Anj,C对映射f而言是Li-Yorke混沌的.任给 (8) 只需证明z1与z2不能同时满足Li-Yorke混沌定义的2个条件时(7)式成立,即证 (9) (10) 不能同时成立. Ηn-1+αδ(In(Enk)0)≤n(2m+1)(1/2η)n-1× |Gi1m×…×Gij-1m×Hijm×Gij+1m×…×Ginm|n-1+α≤ n1+(n-1+α)/2·2m+1+α·ηα< 推论 1任给f∈R,若C⊂In是对f而言的Li-Yorke混沌集合,且 则dimHC≤n-1. 定理 1在C0(In)中,存在剩余集R ⊂C0(In),使得对每个f∈R,若C⊂In对f而言是Li-Yorke混沌的,则C的Hausdorff维数dimH(C)≤n-1,并且C是第一范畴集. 证明由引理1,R是C0(In)的剩余集.根据引理2、引理3和推论1,对∀f∈R,若C⊂In对f而言是Li-Yorke混沌的,则dimHC≤n-1. 往证对f∈R而言的Li-Yorke混沌集合C是第一范畴集即可,即只需证明每一个 是无处稠密的[5]. 因此,对上述i1,…,is-1,is+1,…,in∈{1,2,…,M},is∈{0,1,2,…,M}有 引理 4对于任2个非负实数a、b,下面2条成立: 引理 5设Ci⊂Ini对fi而言是Li-Yorke混沌的,i=1,2,则C1×C2⊂In1+n2对f1×f2而言是Li-Yorke混沌的. 于是 故 再由引理4(ⅱ)得 于是有 从而 引理 6设Ri是Xi的剩余集,i=1,2,则R1×R2是X1×X2的剩余集,反之,若R是X1×X2的剩余集,则R一定是2个剩余集R1与R2的笛卡儿积. 且 故R1×R2是X1×X2的剩余集,类似地可证明第二个结论(略). 定理 2设C0(Ini,Ini)中存在一个剩余集Ri,使得对于每个fi∈Ri,i=1,2,若集合Ci⊂Ini对于fi而言是Li-Yorke混沌的,则 dimH(C1×C2)≤n-1, 且C1×C2是第一范畴集. 证明因为2个疏子集的笛卡儿积是疏子集(易证),所以由命题1和引理5即可证得. 致谢岭南师范学院重点学科项目(1171518004)对本文给予了资助,本文的提出与完成得到了导师熊金城和左再思教授的精心指导和帮助,谨致谢意.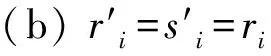
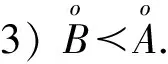
2 n维情形
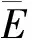
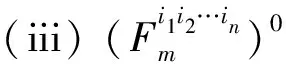
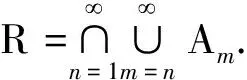
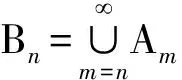
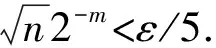
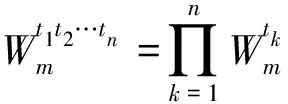
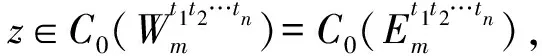
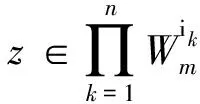
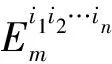
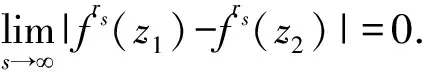
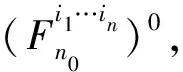
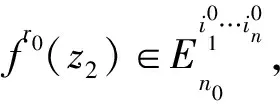
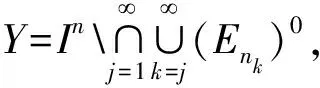
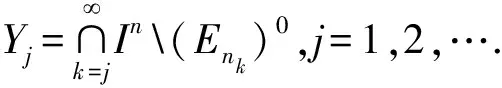
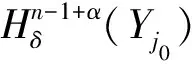
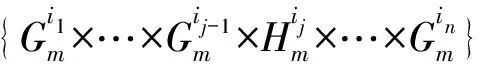
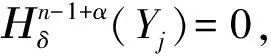
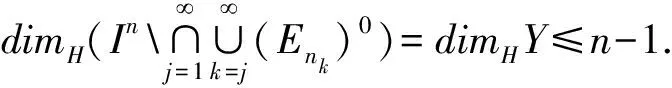
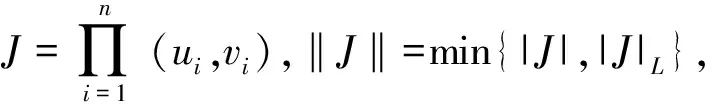
3 n维笛卡尔积情形