分位数模型回归分析
2019-11-09胡良平
胡良平
(1.军事科学院研究生院,北京 100850;2.世界中医药学会联合会临床科研统计学专业委员会,北京 100029 *通信作者:胡良平,E-mail:lphu812@sina.com)
1 概 述[1-2]
1.1 分位数回归模型
1.1.1 分位数
分位数是一种位置指标,一个特定的分位数将任何一个频数曲线下的面积(其数值为1)分为两部分,若小于等于此分位数的观测值个数占全部观测值个数的比例为1/4,则称该分位数为第1四分位数,记作Q1,同理,还有第2、第3四分位数,分别记作Q2、Q3;若小于等于此分位数的观测值个数占全部观测值个数的比例为1/10,则称该分位数为第1十分位数,记作D1,同理,还有第2、第3、……、第9十分位数,分别记作 D2、D3、……、D9;若小于等于此分位数的观测值个数占全部观测值个数的比例为1/100,则称该分位数为第1百分位数,记作 P1,同理,还有第2、第3、……、第99百分位数,分别记作P2、P3、……、P99。
显然,第1四分位数=第25百分位数,即Q1=P25;第2四分位数=第5十分位数=第50百分位数=中位数,即Q2=D5=P50=M(代表中位数);第3四分位数=第75百分位数,即Q3=P75。如此,常用百分位数代替四分位数和十分位数。通过给出一组资料的若干个分位数,可初步描述该组资料的离散程度和分布概况,故在实际工作中,常用百分位数法确定服从偏态分布资料的医学指标的正常值范围。
1.1.2 均值回归模型与均值回归方程
在仅有一个定量自变量和一个定量因变量的简单直线回归分析中,经典统计学中需要事先给出如下几个假定。
其一,正态假定。即当自变量x在其取值区间内取定任何一个特定值xi时,因变量y可以有一组取值与其对应。例如很多身高x为165cm的成年人其体重y是不等的。如此多的y值就会有一个概率分布,粗略地说,该分布可能是正偏态的、对称的(最理想的为正态的)或负偏态的,简单记作P(y|xi),经典统计学假定 P(y|xi)为“正态分布”,对所有的xi都成立。
其二,同方差假定。即当xi取任何值时,其对应的上述正态分布P(y|xi)的方差均相等,称为“同方差”或“方差齐性”。否则,就称为“异方差”或“方差不齐”。
其三,均值假定。即当xi取任何值时,一律采用y的算术平均值y-i取代任何一个yj值,记作y^=y-i|xi。于是,所有的数据点(x,y)可表示为(xi,y^i)。
其四,独立误差假定。即当xi取任何值时,观测值(yj|xi)与其算术均值 y-i|xi(或 y^i)之间的偏差为“误差εi”,假定各误差εi之间互相独立。
基于以上假定且按“普通最小二乘原理或最小平方原理”[3]构建的简单直线回归模型和多重线性回归模型都被称为“均值回归模型”,分别见式(1)和式(2):
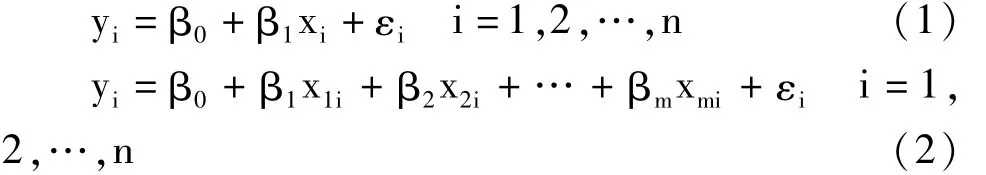
在模型(1)和(2)中,基于样本数据并按最小二乘原理估计出其参数的数值,然后忽略模型中的误差项,就可得到“均值回归方程”,见式(3)和式(4):
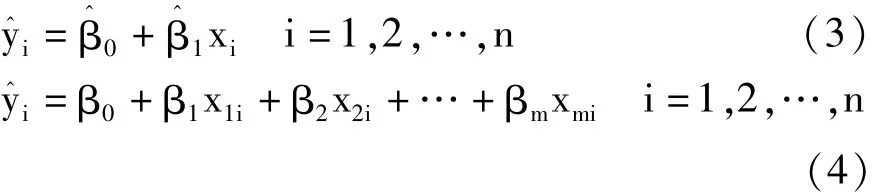
在式(3)和式(4)中,等号左边的“y^i”是在单个自变量xi(在只有一个自变量的场合下)或多个自变量构成的向量(Xi)(在有多个自变量的场合下)取一个或一组特定数值的前提条件下,重复k次观测或试验得到了因变量y的k个观测值的“算术平均值”,简称为“均值”。严格地说,它应该被分别表示成如下的形式,见式(5)和式(6)。
对式(3)而言,y^i的真实含义应该是式(5):
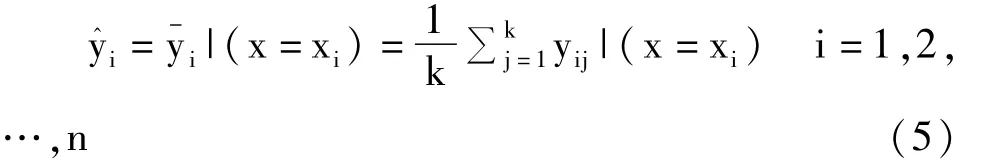
对式(4)而言,y^i的真实含义应该是式(6):
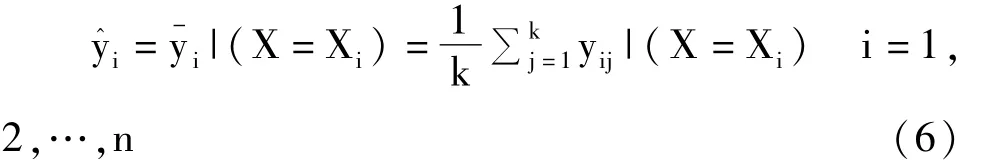
在式(6)中,大写的字母“X”代表由多个自变量构成的向量。
也就是说,常用的简单直线回归模型或方程和多重线性回归模型或方程都属于“均值回归模型或方程”。“最小二乘原理”可用语言表述如下:
在各xi或Xi条件下,求因变量y的任何一个观测值与其模型对应的估计值y^i之间偏差的平方,再将所有各偏差平方求和,称此“和”为“目标函数Q”,设法求其最小值,与此同时,获得求解模型中参数估计值的计算公式。
值得一提的是:对基于最小二乘原理构造出来的目标函数Q求其最小值时,需要将Q中的待估参数视为“变量”,而将各观测点上变量的取值(xi,yi)(一个自变量的情况下)或(x1i,x2i,…,xmi,yi)(m个自变量的情况下)视为“常数”,利用高等数学中求函数“极大值”和“极小值”的方法,即求函数Q关于未知参数的偏导数等多个计算步骤来实现目的。事实上,求得的偏导数又是关于研究问题中“变量(x,y)或(x1,x2,…,xm,y)”的函数,故称其为“导函数”。令求得的导函数为零,就得到若干个方程,其个数为所构建的回归模型中参数的个数。在直线回归模型中,有两个参数,即截距和斜率;在含有m个自变量的多重线性回归模型中,有(m+1)个参数。将这些线性方程联立在一起,就构成了“线性方程组”。求出该方程组的解,就得到了求解待估计参数的计算公式。
1.1.3 中位数回归模型与中位数回归方程
在前面构建“均值回归模型或方程”的“均值假定”中,若用“中位数”取代“算术平均值”,就得到了“中位数回归模型或回归方程”,在有m个自变量的场合下,中位数回归模型见式(7)、中位数回归方程见式(8):
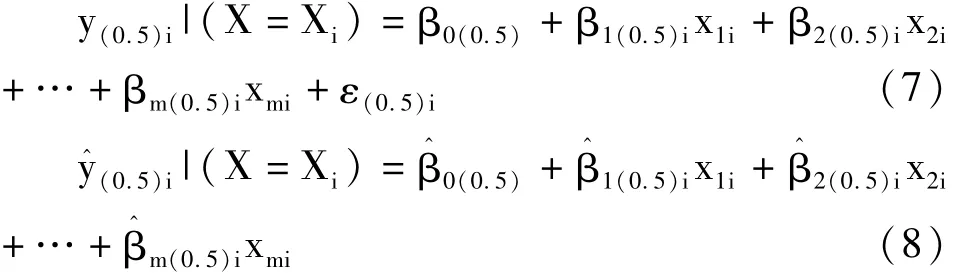
在式(7)和式(8)中,下角标中的i代表观测的编号,i=1,2,……,n;“0”代表“常数项”;“1、2、……、m”分别代表“第1个”“第2个”……“第 m个”自变量;“0.5”代表“第50百分位数”或“第2四分位数”或“中位数”所对应的累计概率,也就是说,“y(0.5)”就是与其对应的“分位数”,即“中位数”。
由前面关于“分位数”的概念可知:“中位数”是一个特定的“分位数”。若将上面的“中位数回归模型或方程”中的“中位数”替换成任意一个分位数“yτ|Xi”,则所得到的回归模型就被称为“分位数回归模型或方程”了。前述的“yτ|Xi”的含义是:在自变量x取特定值xi的条件下,求出全部因变量y的第τ分位数,0<τ<1。当τ=0.5时,就是“第0.5分位数”或“中位数”;当τ=0.25时,就是“第0.25分位数”或“第1/4分位数”,也叫做“第1四分位数”;当 τ=0.75时,就是“第 0.75分位数”或“第3/4分位数”,也叫做“第3四分位数”。
在式(7)和式(8)中,若将“0.5”改换成“τ∈(0,1)”(其含义是0<τ<1),就得到了与第 τ分位数对应的回归模型或回归方程,见式(9)和式(10):
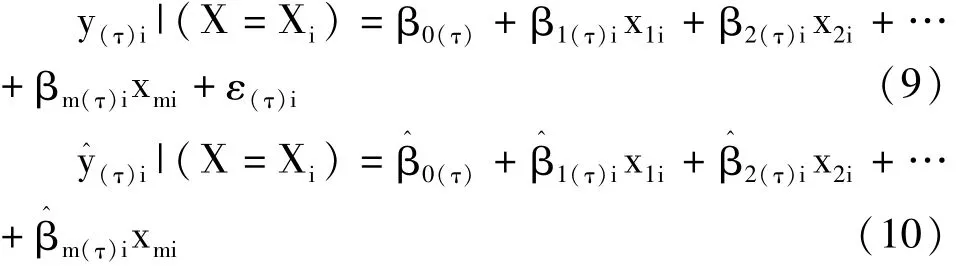
在分位数回归分析中,每给定一个“τ值”,就可求出一个相应的“分位数回归模型或方程”。故对于一个给定的资料来说,因τ在开区间(0,1)范围内有无穷多个取值,就有无穷多个“分位数回归模型或方程”。其中,最常见的分位数回归模型或方程为“第1四分位数回归模型或方程”“第2四分位数回归模型(即中位数回归模型)或方程”和“第3四分位数回归模型或方程”。
1.2 分位数模型回归分析应用的场合
当拟做多重线性回归分析的原始数据中的定量因变量不服从正态分布、有时还存在异方差、资料中存在一定比例的“异常点”且自变量间不存在严重多重共线性时,采用此方法构建多重线性回归模型,可以最大限度地消除资料中违反经典回归分析的“部分或全部假定”对建模结果造成的影响。
1.3 分位数模型回归分析的计算原理
1.3.1 概述
值得注意的是:在求解“均值回归模型”中参数时,是基于“最小二乘原理”推导出来的正规方程组并求解得到的;而当采用“分位数”取代“均值”时,就不适合采取最小二乘原理来构建“目标函数Q”,而需要求因变量y的任何一个观测值与其模型对应的估计值y^i之间偏差的“绝对值”,再将所有各点上的偏差绝对值求和,称此“和”为“目标函数G”。令式(10)等号左边为“W”,则为求解式(10)中参数估计值而构建的目标函数G如式(11)所示:
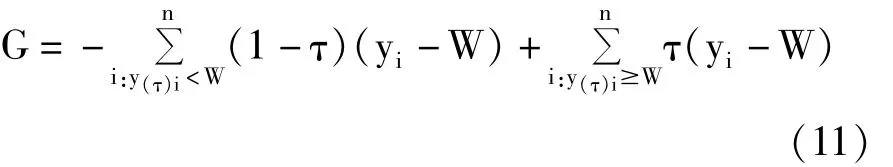
设法求出式(11)的最小值,与此同时,获得模型中参数的估计值,这样求出的参数估计值被称为“分位数回归参数估计值”。
1.3.2 式(11)最小值的计算方法
2.1.1 秸秆产量计算方法 查阅近20篇期刊和论文发现都采用草谷比计算法来估算秸秆产量。其计算方法为:
由 SAS软件的帮助信息[从 SAS/STAT的QUANTREG过程的“details”(即详细情况)菜单进入,其第 2行为“Optimization Algorithms”(优化算法)]可知,求式(11)最小值的计算方法有三种,分别为“简单算法”“内部点算法”和“光滑算法”,在样本含量n<5 000且自变量个数m<50时,三种算法的参数估计结果是基本相同的。
事实上,上述提及的三种算法都相当复杂,涉及到复杂的矩阵运算和反复迭代计算过程。换言之,由式(11)无法给出与各种分位数回归模型或方程中各参数的解析式,即计算公式。故具体分析时,建议采用统计软件来实现计算。因篇幅所限,详细的计算方法此处不再赘述。
2 基于分位数模型回归分析解决实际问题[1]
2.1 问题与数据结构
【例1】假定有一个总样本含量n=1 000的数据集中包含5%异常点的资料,每组数据(即每个个体)包含三个变量(x1,x2,y)的观测值。见表 1。
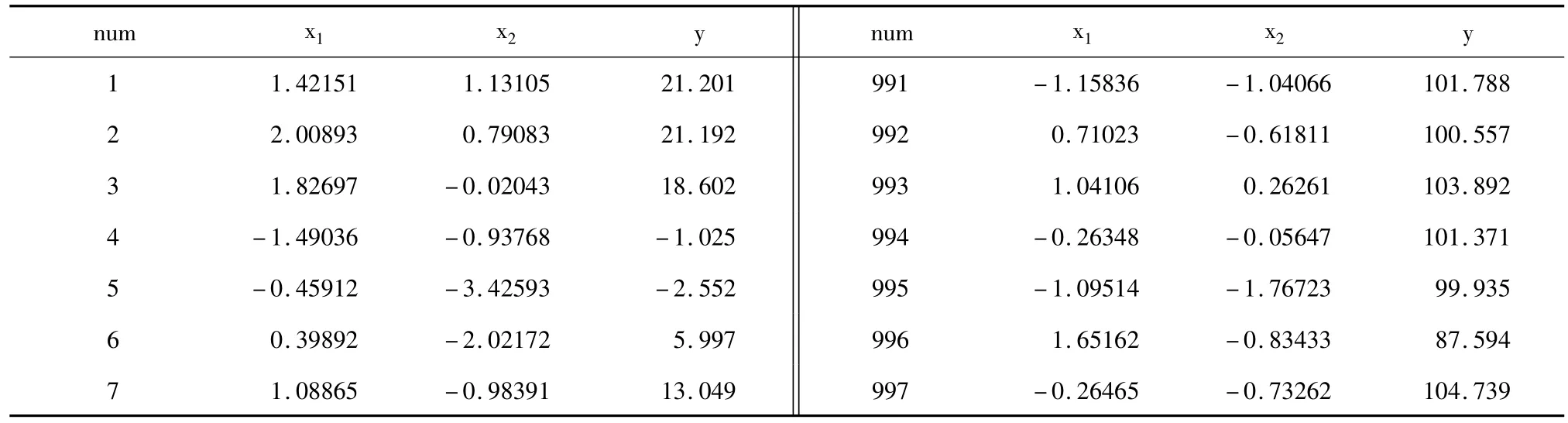
表1 某资料中首尾各10组数据(n=1000)

续表1:
【特别说明】例 1是人为构造的,它来自SAS9.3的QUANTREG过程中的“样例”。三个变量“x1、x2和y”没有实际的专业含义,仅为了造出一个样本含量为1 000且含5%异常点的数据集。
表1中数据构造的方法如下:设定x1和x2及测量误差e都是服从标准正态分布的随机变量(其均值为0、方差为1),前950个y的数值按下面的模型(12)计算出来;后50个y的数值按下面的模型(13)计算出来:
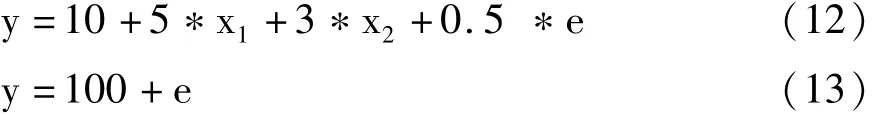
比较式(12)与式(13)可知:y的前950个数据中的每一个都在基数“10”的基础上再加上三项并不大的数值,其平均值约为“10+5+3=18”;而y的后50个数据中的每一个都在基数“100”的基础上再加上一个随机误差,其平均值约为100。由此可知:表1的1000行数据中,对因变量y而言,后50个y值明显大于前950个y值,故属于“异常值”,它们所对应的那50行数据点就属于“异常点”了。
【问题】试拟合表1中y依赖x1、x2变化的二重线性回归模型。
2.2 所需要的SAS程序
2.2.1 产生数据集
先用下面的一段SAS数据步程序产生表1中的1000行3列数据,创建数据集a。
data a(drop=i);
do i=1 to 1000;
x1=rannor(1234);x2=rannor(1234);e=rannor(1234);
if i>950 then y=100+10*e;
else y=10+5*x1+3*x2+0.5*e;
output;
end;
run;
/* 以上程序产生 1000行数据(x1,x2,y),其中,有5%的是异常值*/
以上程序产生的数据见表1。
2.2.2 对资料中因变量y的分布情况进行探索性分析
采用下面的SAS程序对因变量y进行正态性检验并绘制其频数直方图,直观了解y的频数分布情况。
proc univariate data=a;
var y;
histogram y;
run;
以上SAS程序输出结果见表2、图1。

表2 对表1中1000个y值是否服从正态分布检验结果
由表2第1行“W检验”可知,本例中y值不服从正态分布。
图1显示:1 000个y值中的950个在图中左边部分,呈正偏态分布;中间出现了较大一段空缺,还有50个y值位于图中右边部分,其数值波动约为72~120。
2.2.3 对资料进行分位数模型回归分析
下面基于“τ=0.25、0.50和0.75”分别用“分位数回归分析法”来创建二重线性回归模型:
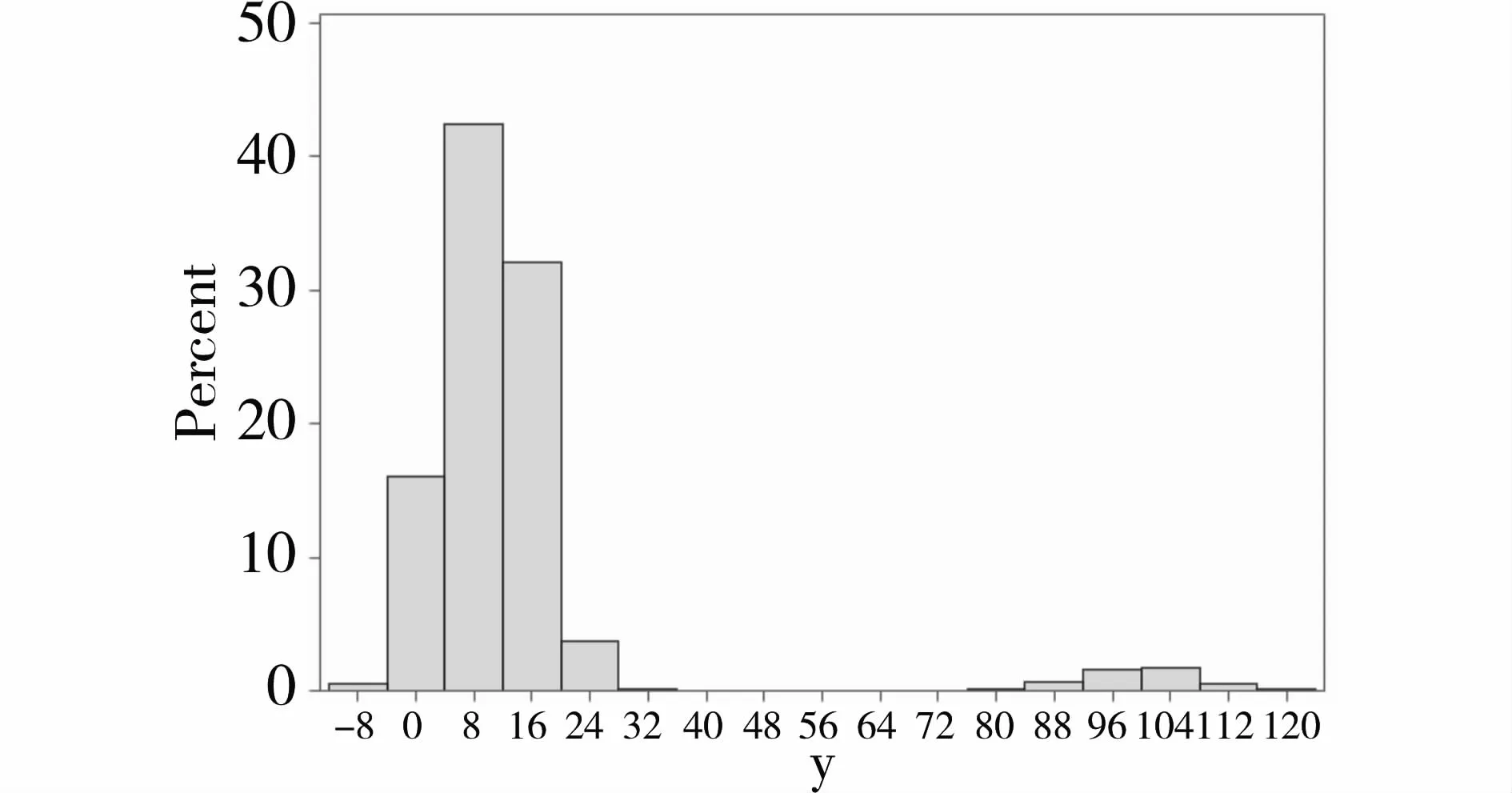
图1 表1中全部1000个y值的频数分布直方图
proc quantreg algorithm=smooth(ratio=.5)data=a;
model y=x1 x2/quantile=0.25 0.50 0.75;
run;
【SAS程序说明】model语句中的选项“quantile=0.25 0.50 0.75”是要求SAS系统分别创建分位数为0.25、0.50(中位数)和0.75的3个二重线性回归模型。
【SAS主要输出结果】
Quantile and Objective Function
Quantile 0.25
Objective Function 1282.8452
Predicted Value at Mean 9.6857

Parameter Estimates
以上是“τ=0.25”对应的“第1/4四分位数回归模型”的参数估计及检验结果

Quantile and Objective Function

Parameter Estimates
以上是“τ=0.50”时对应的“第2/4四分位数回归模型”(即中位数回归模型)的参数估计及检验结果,结果表明:截距项=10.0364、两个自变量的斜率分别为5.0106和3.0294,参考它们的理论值[见式(12)]分别为10、5和3,说明在因变量不服从正态分布且资料中含有5%异常点时,采用“中位数回归分析”创建的二重线性回归模型与其“原模型”之间的吻合程度非常高。
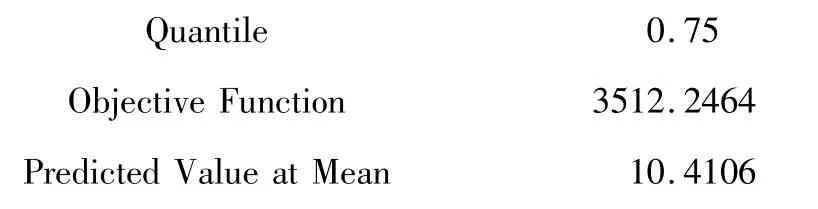
Quantile and Objective Function

Parameter Estimates
以上呈现的是“τ=0.75”时对应的“第3/4四分位数回归模型”的参数估计及检验结果。
2.3 小结[3-4]
2.3.1 采用普通最小二乘法构建二重线性回归模型
proc reg data=a;
model y=x1 x2;
run;
以上SAS程序的主要输出结果如下:
总模型的F=33.76,P<0.0001,表明所创建的二重线性回归模型具有统计学意义;但复相关系数的平方R2=0.0634非常小,表明此二重线性模型的实用价值并不高;模型中三个参数的估计与假设检验结果如下:

变量 自由度 参数估计值 标准误差 t值 Pr>|t|Intercept 1 14.48953 0.62584 23.15 <.0001 x1 1 4.39030 0.62997 6.97 <.0001 x2 1 2.50293 0.60204 4.16 <.0001
以上结果表明:截距项=14.48953,两个自变量的斜率分别为4.39030、2.50293,参考它们的理论值[见式(12)]分别为10、5和3,说明在因变量不服从正态分布且资料中含有5%异常点时,直接基于普通最小二乘原理创建的二重线性回归模型很不理想。
2.3.2 采用“稳健回归分析”创建二重线性回归模型
proc robustreg data=a method=lts seed=100;
model y=x1 x2;
run;
以上SAS程序的主要输出结果如下:
复相关系数的平方R2=0.9933非常大,表明此二重线性回归模型具有很高的实用价值,其参数估计如下:

LTSParameter Estimates
以上结果表明:截距项=10.0054,两个自变量的斜率分别为5.0240和3.0598,参考它们的理论值[见式(12)]分别为10、5和3,说明在因变量不服从正态分布且资料中含有5%异常点时,基于最小截平方和(Least trimmed squares,LTS)法的“稳健回归分析”创建的二重线性回归模型与其“原模型”非常吻合。
2.3.3 总结三种建模方法所得结果的差异
在因变量不服从正态分布且资料中存在异常点时,采用SAS中REG过程并基于普通最小二乘原理直接创建多重线性回归模型的效果很差,而基于“稳健回归分析法”和“分位数回归分析法”得到的结果非常接近。事实上,本例中的数据是基于上面的二重线性回归模型(12)产生的。这个模型意味着:截距项为10、x1前的回归系数为5、x2前的回归系数为3,在此基础上,加一个随机误差的二分之一。此处的“随机误差”是服从均值为0、方差为1的正态分布的随机误差。基于上面的计算结果,可以写出三个二重线性回归模型的具体表达式如下,见式(14)、式(15)、式(16):
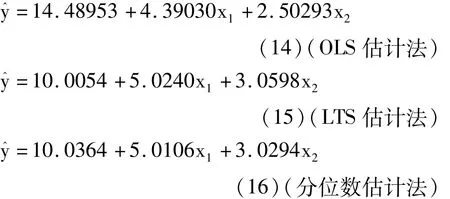
【结论】以模型(12)为“金标准”,模型(14)偏离很远;模型(15)和(16)的质量都很高。相比之下,中位数回归分析的结果稍优于稳健回归分析法(以“回归系数与其真值之间的偏差最小”为评价依据)。
