基于遗传算法的极短弧段天基轨道确定方法

宋可桢 鄂薇 魏承 丁佳欣 赵阳

(1 中国空间技术研究院通信卫星事业部，北京 100094) (2 北京空间飞行器总体设计部，北京 100094) (3 哈尔滨工业大学航天工程与力学系，哈尔滨 150001)

随着航天技术的发展，人类进入与利用太空的能力不断增强，空间目标的数量也随之快速增长，这相应带来的是空间环境与空间安全形势的逐步恶化，为了维护太空资产安全并保持空间优势，美、俄等航天强国深刻意识到空间态势感知的重要性，并将其视为优先发展的重点[1]。天基观测系统作为空间态势感知的重要组成部分，不受气候、大气、地域的限制，更易于实现多种角度观测以及短期内的重访观测，不仅可以与地基系统进行协同配合，也可以作为独立系统进行工作。其中，天基光学观测系统能够获取光度、光谱、纹理、轮廓等大量信息、结构简单且功耗小，已成为在轨观测的主要手段。

在远距离观测过程中，天基光学观测系统只能获得观测目标的测向信息而没有测距信息，可以利用Gauss定轨法与Laplace定轨法对空间目标的初始轨道参数进行求解。由于空间目标与观测平台之间的相对运动速度较快，当以恒星跟踪模式观测时，空间目标的可见弧段极短，观测弧段内空间目标的轨道位形变化微小，利用经典的轨道确定方法会由于求解方程的本征病态无法得到正确的解。虽然目前对极短弧段时长没有准确的定义，但一般可以理解为利用经典的轨道确定方法计算不收敛、难以得到合理解的弧段。

为了能够充分利用极短弧段观测数据，实现对空间目标轨道参数的正确估计，有效提高多个短弧段之间的关联性，并为精密定轨提供有效初值，学者们针对极短弧段轨道确定问题进行了深入的研究。Milani等利用测向角度与角度变化率来描述轨道参数，提出一种利用观测斜距与斜矩变化率的约束域方法来求解极短弧段观测条件下小行星的轨道参数，该方法能够在多段短弧数据下实现轨道确定[2-3]。李骏将这种方法应用到空间目标天基轨道确定中，并提出了约束微分修正方法,实现了利用两段极短弧段数据的空间目标轨道确定[4-5]。王雪莹针对约束域方法运算量大且存在多解的问题，采用粒子群优化算法在约束域内进行优化求解，提高了计算效率[6]。Ansalone等采用遗传算法对极短弧段天基观测数据下的空间目标轨道参数进行估计，该方法将观测弧段内首末时刻的测量斜矩作为优化参数，通过求解兰伯特问题来确定初始时刻的轨道参数，该方法能够有效解决低轨目标的轨道确定问题，但是精度受首末时刻的观测数据误差的影响较大[7]。Hinagawa等采用遗传算法利用地基光学系统对短弧段内的地球同步轨道(GEO)目标进行轨道确定，将轨道根数分为两组作为优化变量分别进行求解[8]，李鑫冉也采用遗传算法来优化求解极短弧段定轨问题，同样选择的轨道根数作为优化参数，该方法利用地基观测平台的观测数据对空间目标的初始轨道参数进行估计，主要的轨道确定对象为低轨空间目标[9-10]。

本文针对极短弧段观测数据下经典轨道确定方法求解精度低的问题，建立了基于遗传算法的空间目标初始轨道参数求解运算模型。为了提高计算效率与避免解收敛到局部最优值，根据空间目标的分布特性进行分区域计算，有针对性地缩小搜索范围，最后在各搜索区域中的优选结果之中选择出最优值。该方法可以为精密定轨提供有效初值，提高多个短弧段之间的关联性，为天基光学观测平台的空间目标监视、跟踪以及编目任务提供参考。

1 基于遗传算法的空间目标初始轨道参数优化求解模型

1.1 空间目标天基观测几何模型

在已知空间目标的观测时刻、单位观测方向向量以及观测时刻天基平台观测轨道位置的情况下，可以计算出空间目标的初始轨道，天基平台观测与被观测空间目标的几何关系如图1所示。

图1中O-XYZ为地心赤道惯性坐标系，rO和rT分别为空间目标和跟踪航天器的位置矢量，l为跟踪航天器指向空间目标的单位向量，ρ为测量斜距。由几何关系可以得到ti时刻

rOi=rTi+ρili

(1)

式中：rOi,rTi为ti时刻空间目标与跟踪航天器在地心赤道惯性坐标系下的位置矢量；li为ti时刻在地心赤道惯性坐标系下跟踪航天器指向空间目标的单位向量；ρi为ti时刻测量斜距。

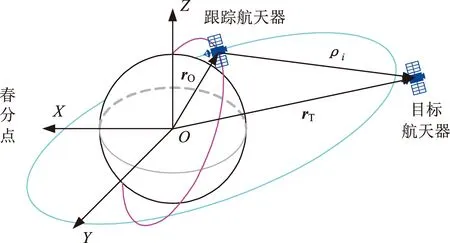
图1 跟踪航天器与空间目标观测几何关系Fig.1 Observation geometrical relationship between chaser and target

1.2 空间目标初始轨道参数优化求解模型的建立

1)优化变量选择

空间目标的轨道可以由一组轨道根数确定，但是采用轨道六根数作为优化参数时，直接优化6个参数的搜索空间维数太大，因此分两次对轨道根数优化λ1=(a,e,M0)与λ2=(i,Ω,ω)。其中a为半长轴，e为偏心率，M0为平近点角，i为轨道倾角，Ω为升交点赤经，ω为近地点俯角。先对λ1中的3个轨道参数进行优化求解，利用这3个参数可以直接计算出ti时刻下空间目标位置矢量rOi，再将λ1作为已知量来优化求解λ2。

生成初始种群时，需要根据一些先验知识或约束条件对优化参数设置取值范围，然后在所设置的值域范围内随机生成种群。本文对空间目标轨道参数进行分区域搜索优化解，最后从各区域中选出最优值。首先根据空间目标的半长轴a分布情况，将搜索范围分为低轨、中低轨与高轨区域，然后根据半长轴a与偏心率e的相关性划分偏心率的取值范围，不同搜索区域种群值域设置见表1。

表1 不同搜索区域种群值域

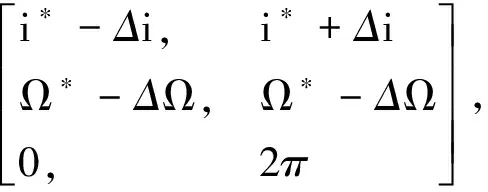
2)初始种群生成与迭代终止条件

初始种群在值域范围内随机选取，以λ1中的优化变量半长轴a为例，在初始生成种群中a的取值可以表示为

ai=ϖamax+(1-ϖ)amin

(2)

式中：amax、amin为优化变量a的值域最大值与最小值；ϖ为随机数，ϖ∈[0,1)。

当优化解收敛趋于稳定时可以停止计算生成子代，本文中当种群计算过程中满足以下条件之一时，迭代计算终止：

(1)当迭代次数大于所设置的最大迭代次数，本文最大迭代数设置为300；

(2)当最优值保持不变所持续的代数大于3时。

3)变异运算

变异运算决定了算法的局部搜索能力，变异概率Pm一般取值为0.01～0.1。变异运算在种群中按照变异概率随机选择染色体，并将各个基因的标准差作为变异量加入到染色体中，作为下一代染色体。变异运算可以表示为

(3)

4)交叉运算

交叉运算决定了算法全局搜索能力，交叉概率Pc一般取值为0.6～0.9。由于采用实数编码，每条染色体上具有3个基因，当(k-1)代进行交叉运算生成k代时，随机从种群中选择两个染色体，然后将e、M0进行交换，或者将M0进行交换。交叉运算表示为

(4)

5)适应度函数

在遗传算法中最重要的部分就是适应度函数的选取，首先给出λ1的的适应度函数。ti时刻下平近点角Mi表示为

(5)

式中：μe为地球引力常数。

通过求解开普勒时间方程，可以得到偏近点角θEi，从而可以得到rOi的模值为

‖rOi‖=a(1-ecosθEi)

(6)

根据观测几何关系，测量斜距ρi可以表示为

(7)

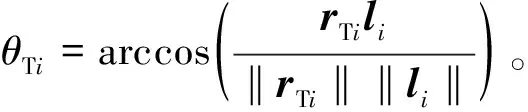
将式(7)代入到式(1)中，可以得到ti时刻下空间目标位置矢量rOi，而ti时刻下的真近点角θRi由θEi表示为

(8)

对于两个时刻(ti,tj),j>i下空间目标真近点角度差值Δθji与rOi,rOj位置向量的之间夹角相同，因此适应度函数可以表示为

(9)

(10)

6)选择运算

选择运算就是以一定的比例从当前种群中选择出适应度较高的个体，令其繁殖产生下一代。本文中选择出适应度排序前10%的个体作为精英个体，但为了保持种群多样性，在剩余的个体中随机选择5%的个体进入到下一代进行繁殖。

2 仿真试验结果与分析

按照试验数据来源的不同，本文的仿真试验分为两部分，第一部分利用空间目标的观测方向向量进行初轨确定计算，观测数据误差来源于图像提取的误差，试验考虑了跟踪航天器传感器对空间目标的可见性条件；第二部分为对比试验，将本文所使用的算法是与同样采用遗传算法但以观测斜矩作为优化变量初轨确定方法以及高斯定轨法进行对比，该部分试验不考虑跟踪航天器传感器对空间目标的可见性，只考虑两者的空间位置关系。

2.1 空间目标初始轨道计算试验

表2为初轨轨道计算仿真试验中空间目标的国际编号以及仿真初始时刻跟踪航天器与观测目标的瞬时轨道根数，以表2中3个空间目标在观测弧段内的观测方向向量作为观测数据，利用本文提出的计算模型对空间目标进行初始轨道确定。在该算例中，跟踪航天器的传感器选择恒星跟踪模式对空间目标成像，相机光轴指向赤经为5°赤纬为10°的方向，同样选择最大观测弧长进行初轨确定。设置初始种群数量为50，变异概率Pm=0.05，交叉概率Pc=0.8，最大迭代次数为300。试验对每组观测数据在3组值域范围内进行计算，并取适应度值最优的一组作为最优解。

表2 观测目标与天基观测瞬时轨道根数

图2为跟踪航天器相机对空间目标进行观测的几何关系，图2中黄色轨道为被观测的空间目标，紫色轨道为跟踪航天器，蓝色视场为跟踪航天器相机观测视场。

图3为3个空间目标的轨道参数λ1=(a,e,M0)与λ2=(i,Ω,ω)进化过程中适应度值的变化，从图3中可以看出国际编号为21989的空间目标两组轨道参数的收敛速度很快，在进化到20代后已经趋于稳定，而且λ1在第一代平均适应值已经小于3″；29422轨道参数的收敛速度较慢，其中λ1是在迭代次数达到上限时停止迭代的，最优的适应度值也较大；29444轨道参数中λ1收敛的速度较快，而参数λ2也是在迭代次数达到上限时停止迭代的，最优适应度值相对于21989而言较大，主要原因是由于21989为高轨目标，相对运动速度较慢，采集到的观测数据量相对于其他两个目标的较多，拟合精度高于中、低轨目标。

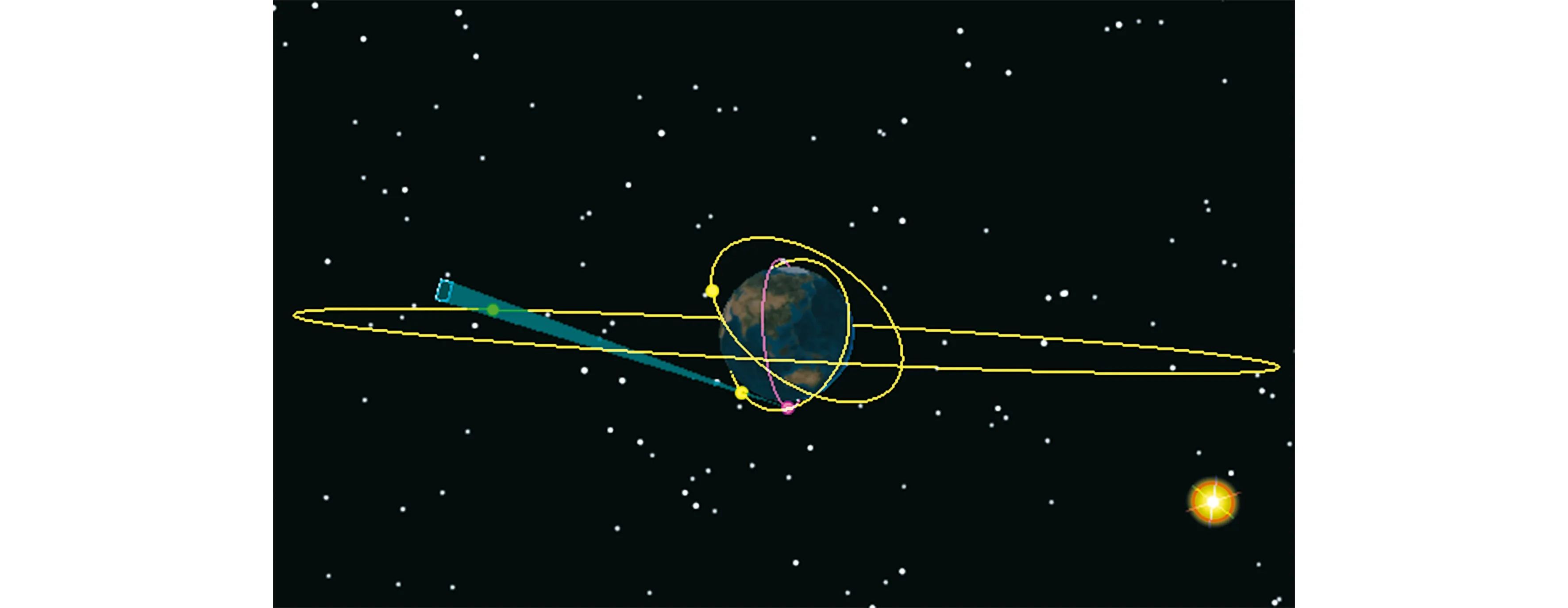
图2 跟踪航天器相机对空间目标的观测几何关系Fig.2 Observation geometrical relationship between sensor and targets

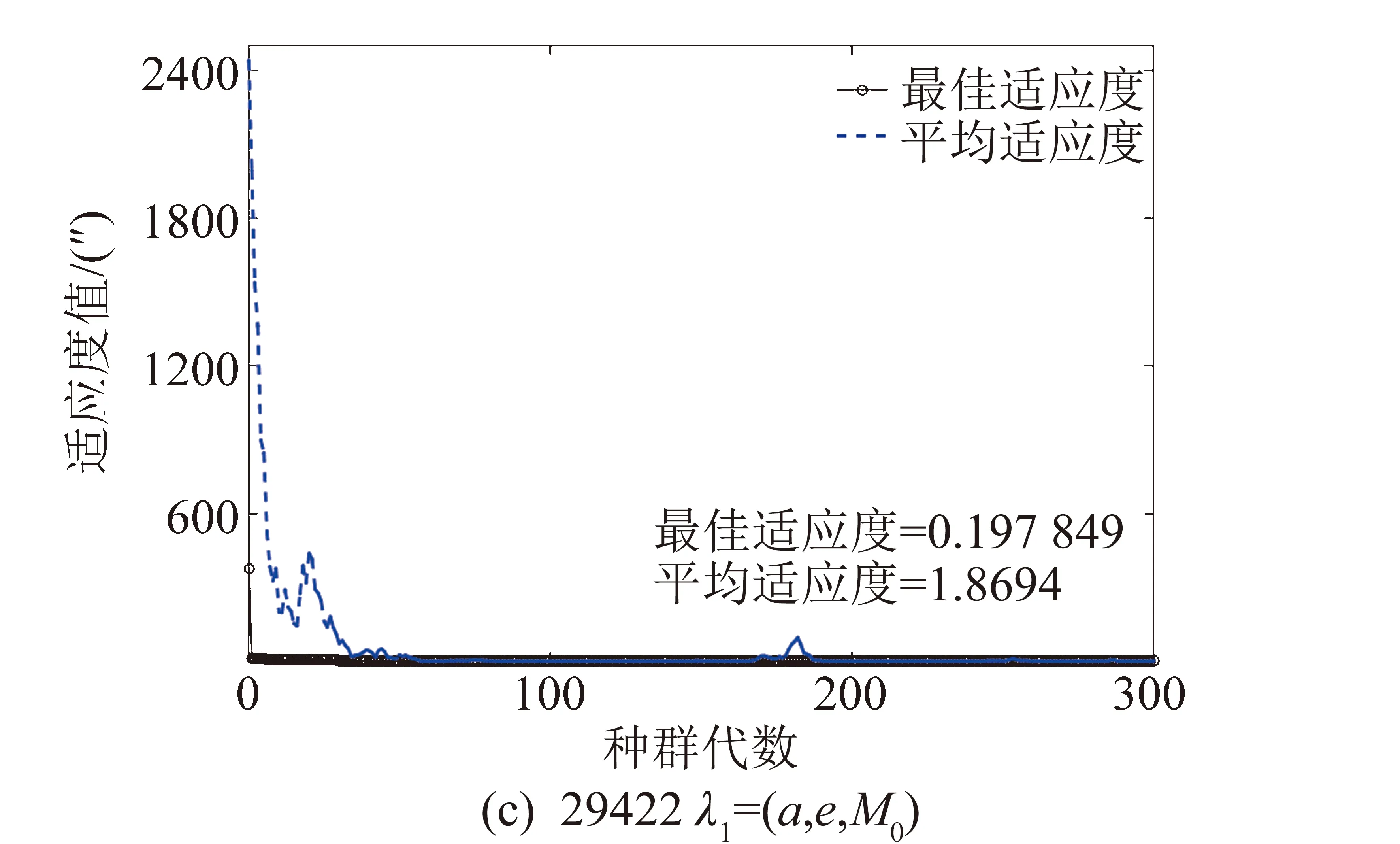
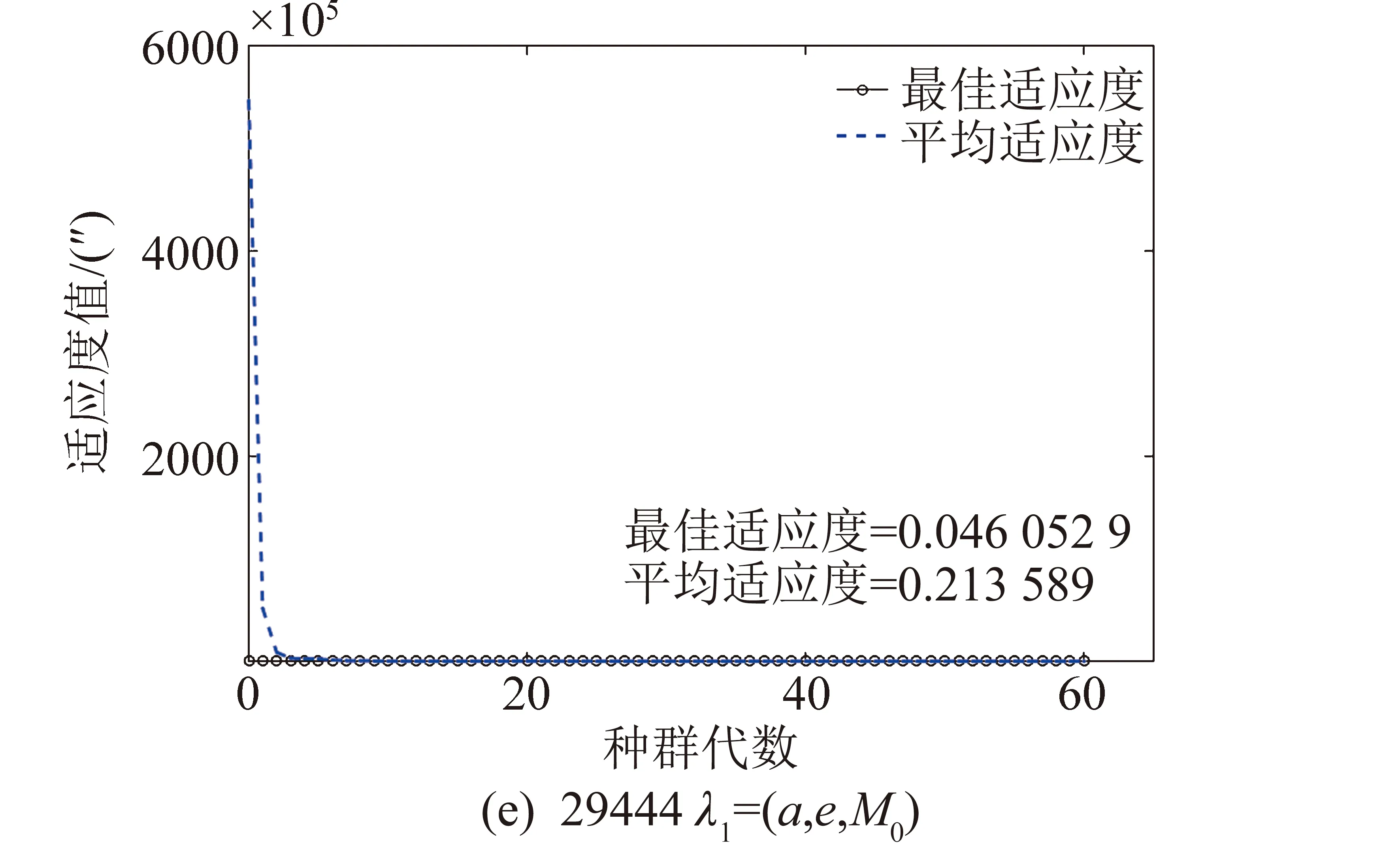
图3 优化轨道根数的适值收敛过程Fig.3 Convergence process of the fitness value of orbit coefficien

表3给出了3个空间目标定轨误差，其中，观测时长为26 s的中轨目标29 422误差较大，半长轴的误差达到100 km，偏心率最大误差可达0.041 8；观测时长为42 s的低轨目标294 44误差相对较小，半长轴误差为22 km，偏心率误差为0.000 8；观测时长为364 s的高轨目标219 89误差最小，半长轴误差为12 km，偏心率误差0.001 9。3个空间目标除平近点角外其他4个角度类型的轨道根数误差都较小。

可以看出，轨道参数的精度随观测弧长的减小而降低，相对于无法计算出合理解的传统定轨方法，采用遗传算法计算空间目标轨道参数具有一定优势，并且这种定轨精度能够满足空间目标初始轨道确定的精度要求，能够为相同空间目标的多段短弧数据提供关联性，并为后续的精密定轨提供有效初值。

表3 遗传算法对不同空间目标的定轨误差

2.2 不同算法对比试验

为了验证本文所使用算法的优势，将本文所使用的算法与文献[10]中同样采用遗传算法但以观测斜矩作为优化变量初轨确定方法以及高斯定轨法进行对比，该部分试验不考虑跟踪航天器传感器对空间目标的可见性，只利用两者的空间位置关系计算空间目标单位观测方向向量，并将角度噪声加入到观测方向向量中。对比试验部分的跟踪航天器与观测目标的轨道参数见表4，该算例以60 s的观测数据进行初始轨道计算。

表4 观测平台与观测目标的轨道参数

首先给出将角度噪声加入到观测方向向量的方法，在地心赤道惯性(ECI)坐标系下的观测方向向量l可以表示为l=lxrex+lyrey+lzrez，其中，rex、rey、rez分别为惯性坐标系的坐标轴单位向量，因此选择任意一个方向与l不平行的坐标轴方向向量，令rh=l×rex，令l绕rh旋转角度β1，β1是一个符合高斯分布的角度噪声，旋转后的向量可以表示为

l1=lcosβ1+(rh×l)sinβ1

(11)

将l1绕l旋转角度β2，β2符合0～2π之间均匀分布，利用Rodrigues旋转方程加入噪声，加入噪声后的空间目标观测方向向量lm可以表示为

lm=l1cosβ2+(l×l1)sinβ2+

l(l·l1)(1-cosβ2)

(12)

按照该方法可以对空间目标观测方向向量加入角度类型的噪声，由于每组试验中所产生的误差都具有随机性，因此试验采用蒙特卡洛仿真方法，每次试验采用1000组具有不同随机误差的观测方向向量数据进行轨道计算，并取1000组仿真试验结果的平均值作为最终计算结果。图4为本文所采用的算法，且测量数据为1″随机误差的蒙特卡洛仿真结果，图4中红色圆点为仿真结果，蓝色方点为真值。从图4中可以看出，计算出的轨道根数分布集中于真值周围，远离真值附近的仿真算例中测量数据误差较大，其中半长轴与偏心率的误差分布较大，而能够确定轨道面的轨道倾角i与升交点赤经Ω误差相对较小，轨道倾角i的误差分布主要在4°范围之内，升交点赤经Ω的误差分布主要在3°之内，对于偏心率较小的近圆轨道近地点幅角与平近点角的误差会较大，但是可以看出两者之间具有斜率为-1的线性比例关系。

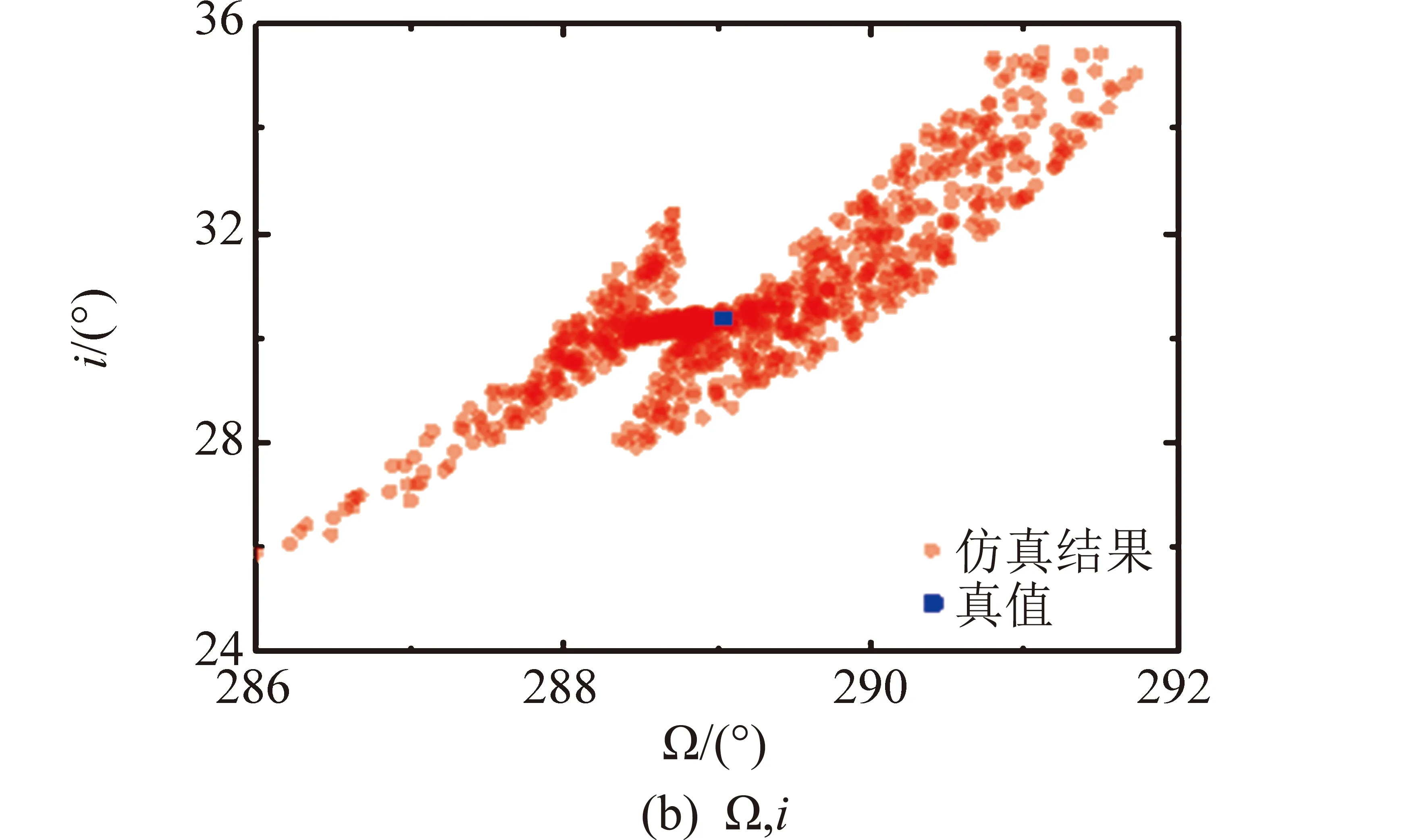
图4 轨道根数优化解与真值分布Fig.4 Optimal solution and truth value of orbit coefficient

将本文所使用的以轨道根数作为优化变量的轨道参数求解方法、文献[10]中以采观测斜矩作为优化变量的轨道参数求解方法以及Gauss定轨法进行对比，表5为空间目标观测方向向量的误差分别为1″、2″、3″情况下3种算法的定轨误差。从表5中可以看出，3种算法的定轨精度都随观测方向向量误差的增大而增大，Gauss定轨法的定轨精度明显低于基于遗传算法轨道确定方法，而采用轨道根数作为优化变量的方法优于采用观测斜矩作为优化变量的方法，同时利用轨道六根数作为求解优化变量能够避免了求解兰伯特问题，降低了适应度函数的复杂度与计算量，而且减少首末时刻测量数据误差影响的程度，更适用于解决空间目标极短弧段轨道确定问题。

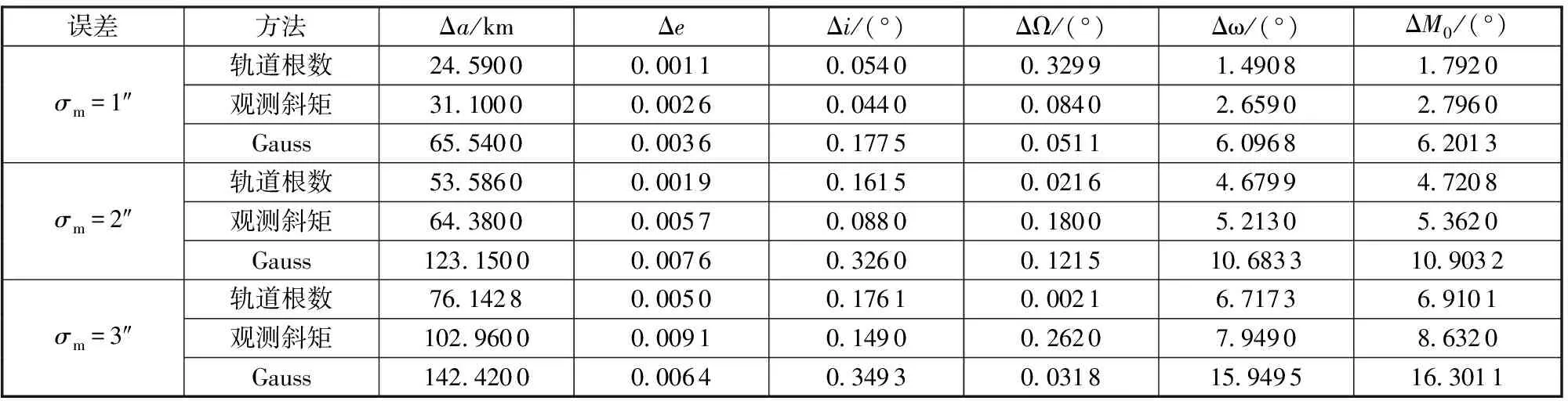
表5 不同误差下三种算法的定轨误差

3 结束语

文章针对天基观测可见弧段较短利用经典轨道确定方法无法获得合理解的问题，采用遗传算法对空间目标极短弧段天基轨道确定问题进行优化求解，并利用轨道根数作为优化变量。通过分析空间目标的在轨分布特性，按照轨道高度将搜索空间进行划分，从而缩小了搜索范围提高了计算效率。通过与不同算法进行对比，采用轨道根数作为优化变量的方法优于采用观测斜矩作为优化变量的方法与Gauss定轨法，利用轨道六根数作为求解优化变量能够避免了求解兰伯特问题，降低了适应度函数的复杂度与计算量，而且减少首末时刻测量数据误差影响的程度，更适用于解决空间目标极短弧段轨道确定问题。该算法对于利用极短弧段观测数据的初始轨道确定计算效率与精度较高，具有较强的工程实用性。