应用GNSS定位数据的微小卫星自主导航方案设计

刘燎 吴爱国 陶钊榕 孙华苗 谢成清

(1 哈尔滨工业大学(深圳)，广东深圳 518055) (2 深圳航天东方红海特卫星有限公司，广东深圳 518064)

随着低成本全球卫星导航系统(GNSS)接收机(包括美国的GPS及中国的“北斗”导航系统)的应用[1]，在微小卫星上利用GNSS接收机进行实时轨道确定进而提高其自主能力，已成为一种发展趋势[2]。一个完整的自主导航系统应包括卫星实时定轨和轨道预报功能，使卫星能自主完成星上任务规划。通常，轨道预报的计算方法有数值方法和解析方法2种。数值方法计算精度较高，适用于实时的状态递推；缺点是耗费大量机时，且难以完成预报。解析方法利用解析模型快速地预报任意时刻卫星的位置、速度；缺点是精度较低[3]。目前，应用GPS定位数据的卫星实时轨道确定主要采用卡尔曼(Kalman)滤波[4]及基于轨道动力学模型的轨道确定技术。但是，对于采用这种轨道确定技术的导航系统，其结果很难用于长期的在轨星历预报(例如几个轨道周期后甚至几天后的轨道预报)，且往往需要占用大量的星载计算机机时，因而不适用于长期轨道预报[5]。文献[6]中提出了一种采用简化的动力学模型和一种嵌套插值算法的积分器，但是也需要高性能的星载计算机，不适合应用于微小卫星的轨道预报。文献[7]中对基于GPS定位数据的卫星轨道预报算法进行研究，但并未对卫星实时轨道确定方法进行研究。

针对目前常用的近地圆轨道，本文设计一种应用GNSS定位数据的微小卫星自主导航方案，可进行自主轨道确定和预报。自主导航模块根据GNSS定位数据，采用一种改进的数值积分方法，可进行在轨实时轨道确定，且计算量相对较小，可解决采用解析动力学模型精度较低的问题。同时，GNSS定位数据发送给星历模型生成模块，利用基于UD分解的Kalman滤波技术进行星历参数的在轨估计，在GNSS接收机故障或者定位数据无效的情况下，利用星历参数进行轨道预报，提高卫星的自主能力。

1 导航方案设计

本文提出的自主导航方案系统框图见图1。首先，GNSS接收机生成的定位数据发送给自主导航模块，采用基于4阶龙格-库塔法和Richardson外插法及扩展Kalman滤波方法进行导航运算[7]，对卫星在惯性坐标系下的位置和速度矢量进行估计，根据状态估计值生成飞行轨迹插值多项式，再将该插值多项式发送到轨道预报模块。轨道预报模块根据自动导航模块发送的轨迹插值多项式，按制导和控制周期要求生成当前时刻的轨道状态数据。考虑到备份的要求，GNSS接收机生成的定位数据同时发给星历模型生成器，后者根据解析轨道模型，采用Bierman UD分解形式的Kalman滤波技术对相关星历模型参数进行在轨估计[8]。该导航方案可对任意时间间隔的卫星星历进行预报，不必按步长对轨道进行积分，其计算量相对较小，对星载计算机的性能要求不高，可满足微小卫星的使用要求。当GNSS接收机出现故障后，估计得到的轨道参数可作为备份[9]，确保卫星在轨飞行时能获得轨道信息。

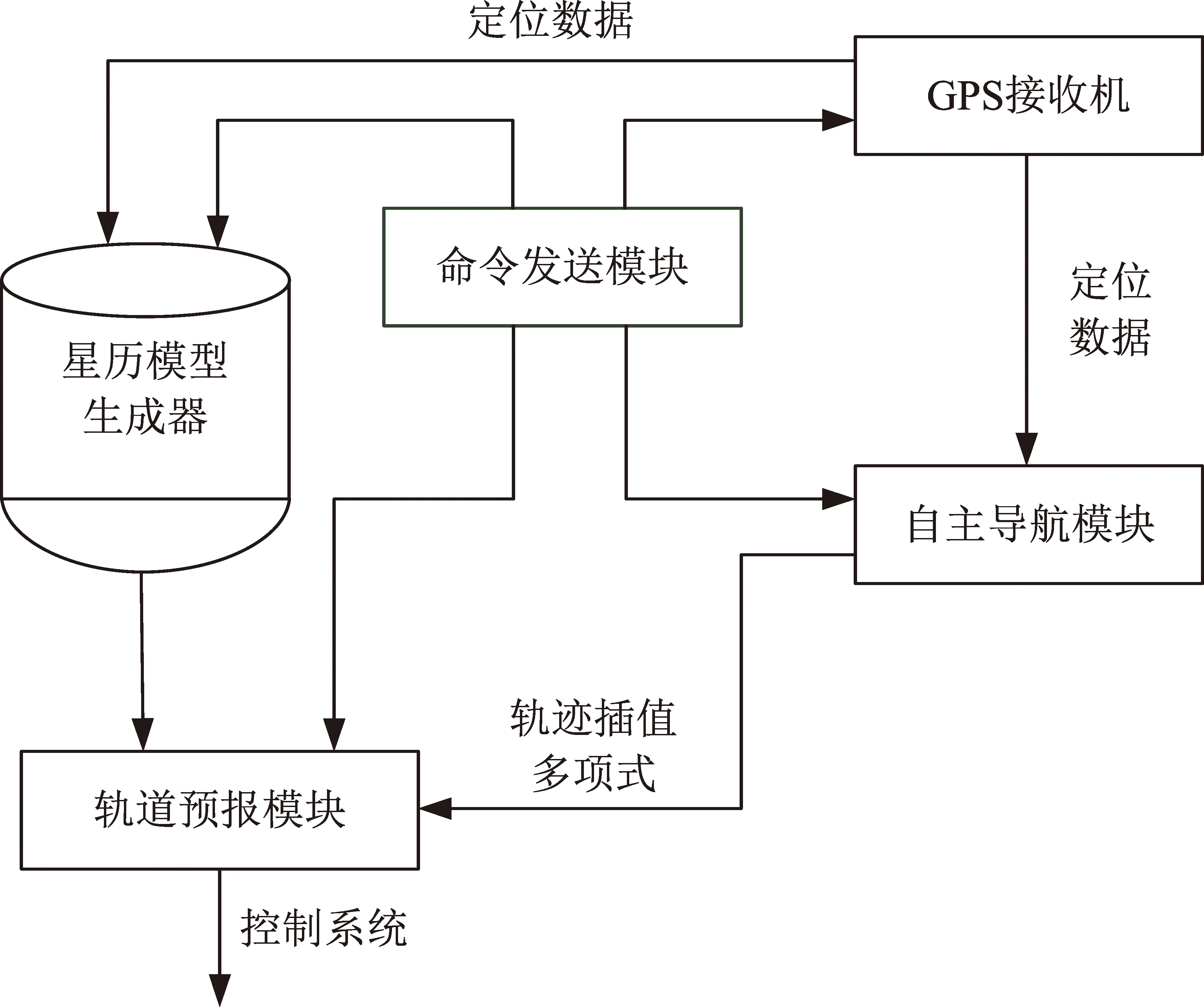
图1 导航方案系统框图Fig.1 Navigation scheme system block diagram

在上述导航方案中，需要解决自主导航模块中对于轨道状态的计算和星历模型生成器中对于星历参数的在轨估计问题。

1.1 轨道状态计算

自主导航模块根据GNSS定位数据，采用基于4阶龙格-库塔法和Richardson外插法及扩展Kalman滤波进行导航运算，对卫星在惯性坐标系下的位置和速度矢量进行估计。

1)轨道动力学模式选择

分析表明，在低轨近圆轨道上，太阳、月球引力摄动及太阳辐射压力的影响可忽略不计，大气阻力的影响相对较大，但由于测量信息频度较高，可随时更正，因此仿真分析中可忽略[8]。地球引力场模型采用4×4阶的JGM-3模型已能满足精度要求，考虑余量，本文中地球引力场模型取6×6阶。

2)运动方程及数值积分算法

卫星所受地球引力摄动加速度为

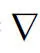
(1)

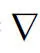
(2)

式中：地心距r=‖r‖，r为卫星在J2000.0地心赤道坐标系中的位置矢量矩阵形式；λ和φ分别为卫星地心经度和纬度；GM和RE分别为地球引力场系数和地球赤道平均半径；非球形谐函数Cnm和Snm表示地球非球形引力场；Pnm为n阶m次的缔合勒让德多项式。

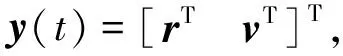
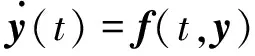
(3)

式中：卫星的状态方程f可表示为状态变量y和时间t的函数。

本文采用一种基于4阶龙格-库塔法和Richardson外插法的数值积分算法(RK4R)。在[t,t+2h](t和h分别为积分时间和积分步长)内进行3次RK4数值积分，积分步长分别为[t,t+h]，[t+h,t+2h]，[t,t+2h]。完成数值积分计算后，根据Richardson外插法，对轨道状态变量y(t+h)和y(t+2h)进行修正，从而提高计算精度。

3)轨道参数滤波算法

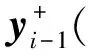
(4)

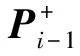
Kalman增益矩阵表达式为

(5)

式中：R为测量误差方差矩阵；雅克比矩阵Gi=∂zi/∂y，zi为卫星状态的测量值。

状态测量值的更新及其相应的协方差矩阵为

(6)

式中：g为测量方程。

(7)

1.2 星历参数在轨估计

本节利用GNSS定位数据对星历参数进行在轨估计，得到星历参数可进行轨道计算和预报，作为轨道参数信息的备份和进行轨道预报等相关信息计算。图2为星历参数估计流程。

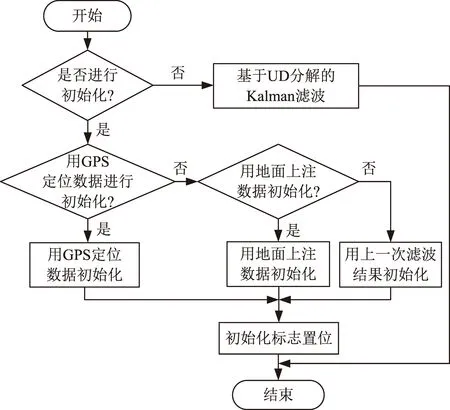
图2 星历参数估计流程Fig.2 Ephemeris parameter estimation flow

1.2.1 算法说明

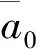
本文算法的计算过程可描述为：根据标志判断是否需要初始化；若此时需要进行初始化，根据GNSS定位数据进行滤波器初始化；若本次计算过程中初始化已完成，则进行Kalman滤波计算。利用GNSS定位数据对历元时刻轨道平根数滤波器进行初始化，该初始化过程可描述为：将GNSS测量得到的位置和速度矢量转换为J2000坐标系下；将J2000坐标系下的位置和速度矢量转换为瞬时轨道根数；通过迭代过程计算平均根数，并给出对应的星历模型参数；根据提供的参数计算状态误差协方差矩阵，并进行UD分解；输出GNSS时刻对应的星历模型参数以及初始U0阵和D0阵。

1.2.2 滤波算法

滤波流程如图3所示。

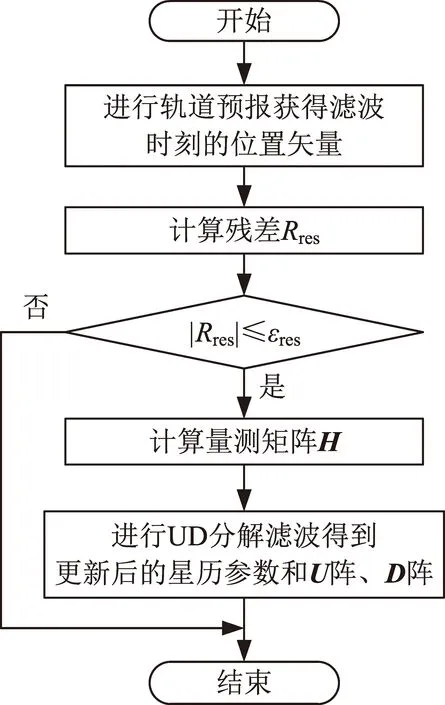
图3 滤波流程Fig.3 Flow of filter

利用基于Bierman UD分解Kalman滤波算法对星历参数进行滤波，得到更新的星历参数以及协方差矩阵对应的U阵和D阵，主要计算步骤如下。

(1)根据滤波得到的星历模型参数X-以及其对应的历元时刻t0，进行轨道预报，得到当前GNSS定位数据时刻tGNSS对应的卫星位置矢量。

(2)计算残差。若残差大于给定的容限，则判断为野值，退出当前滤波过程；否则，执行步骤(3)。

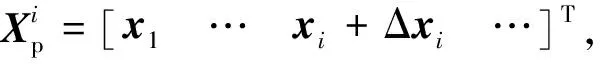
(8)

式中：RZ为绕J2000坐标系Z轴的旋转矩阵；S为tGNSS时刻对应的格林威治恒星时角。

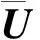
(9)

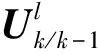
(10)

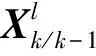
2 仿真验证

本文采用内部不带导航算法的GNSS接收机。这种类型的接收机完成对GPS卫星信号的接收后，仅进行简单的处理，直接输出定位数据。其优点是初始化时间短、可靠性较高；缺点是定位解的速度精度较差。用MATLAB软件对本文方案进行数学仿真验证，仿真条件如表1所示。

对于仿真条件，不同轨道高度的滤波(定位)精度如图4所示。对于500 km轨道高度，轨道滤波精度在40 m以内；600 km轨道高度，滤波精度在30 m以内；700 km轨道高度，滤波精度在25 m以内。

在GNSS数据无效的情况下，采用轨道递推的形式，滤波时间和轨道预报精度如图5所示。可以看出：滤波时间为2天，预报时间5天以内，轨道预报精度基本在15 km以内，可满足中低精度的微小卫星任务需求。其中，滤波时间2天情况下，对于3种轨道高度，轨道预报精度时间曲线如图6所示。

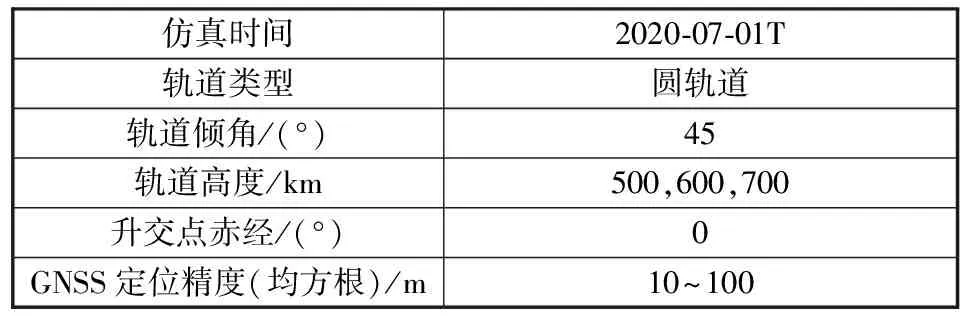
表1 仿真条件

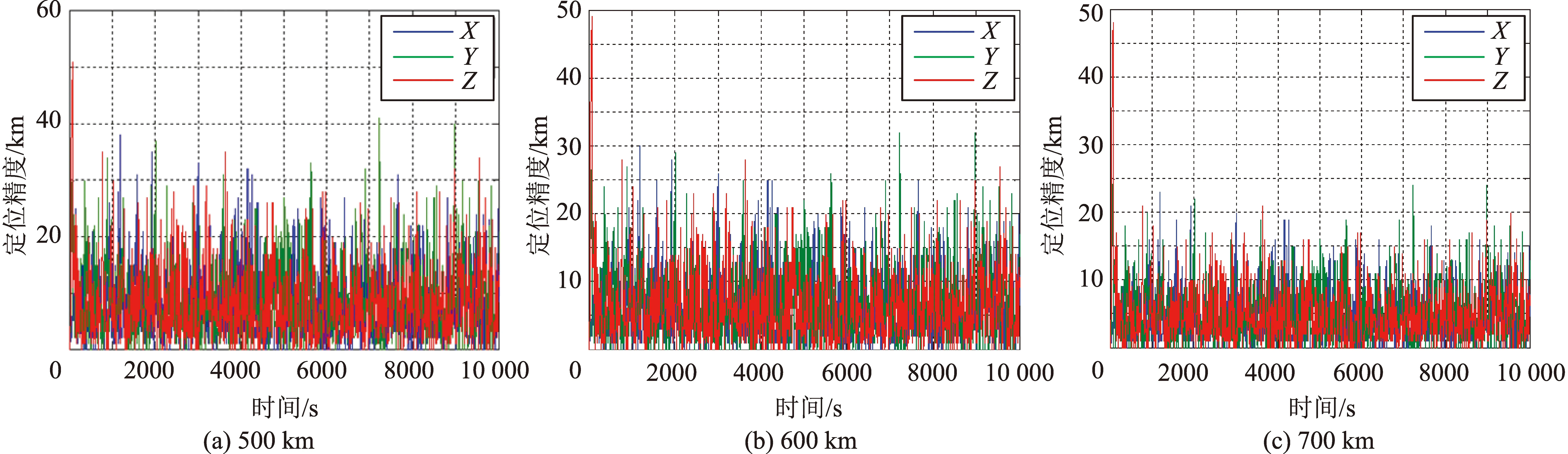
图4 3种轨道高度的滤波精度Fig.4 Filter accuracy for three orbit altitudes

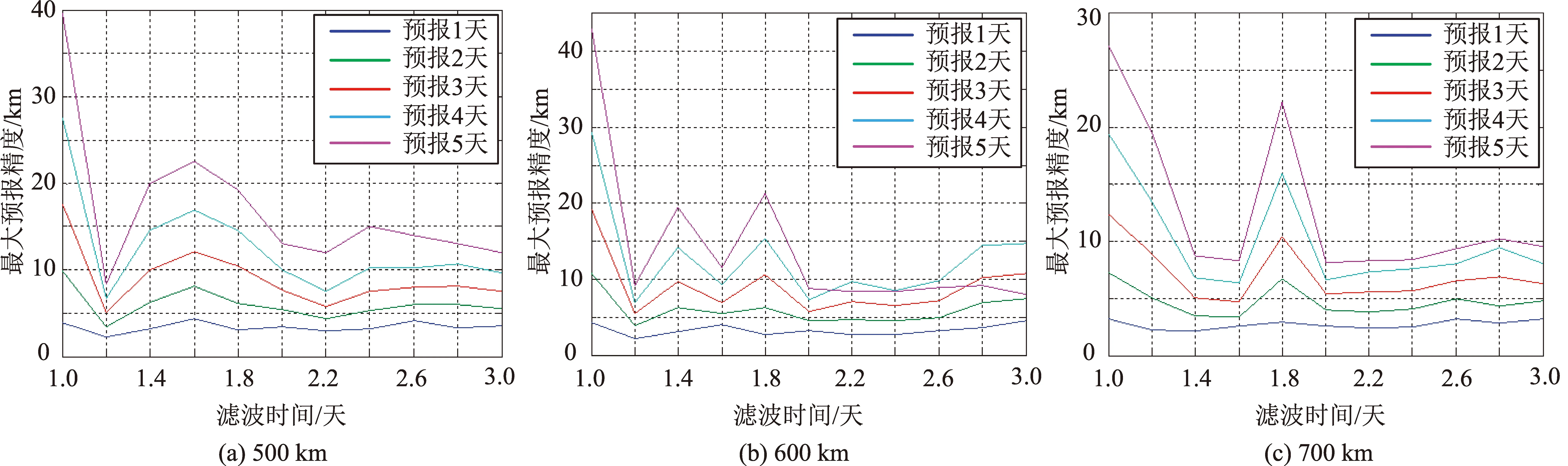
图5 3种轨道高度的预报精度Fig.5 Prediction accuracy for three orbit altitudes

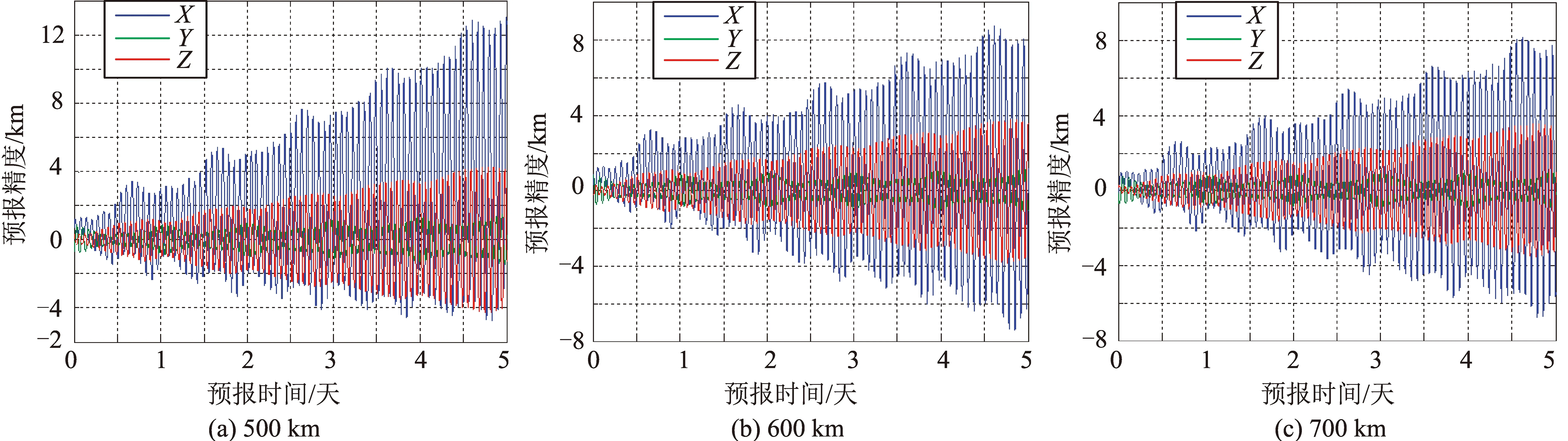
图6 滤波2天的预报精度Fig.6 Prediction accuracy for 2-day filter time

从以上仿真结果分析，700 km滤波精度在25 m以内，可满足一般微小卫星0.1°指向精度的要求。预报精度基本在15 km以内，也可满足微小卫星1°指向精度的要求和对进出地影区和地面站时间的预报精度要求。随着轨道高度的增加，相同滤波时间和预报时间下，预报精度会提高，主要是由于随着轨道高度的增加，气动力对轨道的干扰在减小，1000 km以上影响基本可以忽略不计。因此，本文提出的导航方案可以满足大部分微小卫星的中等精度指向精度和轨道预报任务要求，同时可显著提高微小卫星的自主性，降低地面测控系统的压力和成本，具有良好的工程应用前景。

3 结束语

本文针对微小卫星长期自主运行需求，研究了应用GNSS定位数据的微小卫星自主导航方案。该方案主要根据GNSS定位数据提高卫星在轨的自主性：根据GNSS定位数据进行滤波生成轨迹插值多项式(初始化时间短)，可生成当前时刻的轨道状态数据和进行轨道预报。同时，又考虑到备份的要求，根据解析轨道模型来估计平均轨道参数，当GNSS接收机出现故障后，确保卫星在轨飞行时能获得轨道信息。在轨道动力学选择过程中，本文地球引力场模型取6×6阶，在选取高阶引力场模型的基础上，在轨实时轨道确定能否达到10 m以内和预报精度能够达到10 km以内，并且如何减少对计算机计算量的需求，可作为下一步研究的内容。