内压作用下焊制四通的塑性极限分析
2019-11-08刘张羽1虎1陈照和
刘张羽1,孙 亮,惠 虎1,陈照和
(1.华东理工大学,上海 200237;2.中国特种设备检测研究中心,北京 100013)
0 引言
焊制四通是物料生产和运输的重要元件,广泛地应用于石油化工、电力及油气运输等工业领域[1]。由于焊制四通几何结构复杂及数学分析较为困难,至今尚没有成熟简易的理论分析方法或工程估算公式。根据ASME锅炉及压力容器规范第Ⅷ分卷第二册另一规则[2]及我国压力容器分析设计规范JB 4732[3]的规定,如果容器的外载小于极限载荷下限值的2/3,则无需满足一次薄膜应力及一次弯曲应力的强度条件。焊制四通的塑性极限载荷是进行结构设计和评价四通极限承载能力的重要参数。
从“九五”科技攻关到“十二五”科技攻关期间,相关学者对无缺陷直管、弯管以及三通的塑性极限载荷进行了系统地研究,并提出了相应的解析解或估算公式。ASME B31G[4]给出了直管塑性极限载荷解析解,韩良浩等[5]对该解析解与有限元数值解进行比对,发现结果十分吻合。Goodall等[6-7]按照von-Mises屈服准则推导了无缺陷弯管的塑性极限压力计算式,并通过试验对该式进行了验证。轩福贞等[8-9]分别提出了焊制三通的解析式及工程估算式,其中文献[8]还推导了等壁厚等径挤压三通[10]的解析式。然而,压力管道系统特别是油气开采及输送管道中还存在着四通、六通等管道元件,目前国内外没有人给出四通的解析解及工程估算公式。四通的几何结构非常复杂,存在局部的几何形状不连续,在主管与支管的相贯线处会形成很大的应力集中,即使在正常的工作条件下,该处的应力也有可能会达到屈服应力[11]。因此,对无缺陷四通极限载荷的研究是很有必要的。
内压是管件最常见的工作载荷,也是四通进行结构设计及强度校核时必须考虑的载荷。本文采用弹塑性有限元的方法对四通的塑性极限内压进行系统地研究。参考前人对三通的研究,通过对主管径厚比、支主管径比、支主管壁厚比等尺寸参量的计算和分析,找到了影响四通极限内压的主要因素,发现三通研究中的Ptd参量[12]不适用于四通。通过对200多个四通有限元算例的数据进行分析整理,建立了覆盖不同尺寸范围的四通的塑性极限内压数据库,在数据库的基础上拟合出形式简单且精度较高的塑性极限内压工程估算式,并与直管、焊制三通的计算公式进行比较,为以后研究含缺陷四通塑性极限内压及其安全评定提供技术支撑。
1 四通塑性极限内压有限元分析
为全面考虑各个因素对四通塑性极限内压的影响,选取主管径厚比B、支主管径比A、支主管壁厚比C及Ptd(C/A)等4个无量纲参量,对这些参量进行组合,确保研究能覆盖到尽量多的不同尺寸范围的四通。制定了下列不同参量组合的计算方案:
(1)主管外径与壁厚比B(B=D01/T1):5,10,15,20,25,30;
(2)支主管外径比A(A=D02/D01):0.5,0.6,0.7,0.8,0.9,1.0;
(3)支主管壁厚比C(C=T2/T1):0.5,0.6,0.7,0.8,0.9,1.0;
(4)Ptd[Ptd=(T2/T1)/(D02/D01)]:1.0,1.1,1.2,1.3,1.4,1.5。
1.1 有限元模型
在进行有限元分析时,不考虑主、支管的椭圆度和加工误差,将四通简化为两个相贯的圆筒体形成的结构(见图1)。模型尺寸选自采油树的7寸大四通实体:主管外径238 mm,主管长度420 mm,支管长度530 mm。通过对1/2模型、1/4模型及1/8模型的计算结果进行比较,发现极限内压数据的误差在1%以内,其中1/8模型的计算结果是相对较为保守的。因此,在进行有限元建模时,选择采用四通的1/8子模型,如图2所示,这样的简化可以大量减少模型的单元数,从而一定程度上减少了计算量,并且保证了得到的极限内压结果偏于保守。

图1 焊制四通结构示意
采用20节点等参元(Solid 186)对模型进行网格划分。单元数量过少会导致计算结果不准确,而单元数过多又会增加计算时间。通过大量的试算,确定了一种较为合理的网格划分方式,即通过应力梯度来确定网格的疏密程度,在主支管的相贯区及附近进行网格加密,远离相贯区的区域采用较为稀疏的网格。通过对网格的无关性验证,网格层数大于6层时,计算结果基本相同,考虑计算资源以及时长,确定主支管沿壁厚方向的层数为8层。模型的单元数在15 000~30 000之间,可以保证计算结果的准确性。典型的网格划分模型见图3。

图3 典型网格划分示意
1.2 边界条件、载荷及材料假设
选择采用四通的1/8子模型,在四通的3个对称面上施加对称约束。将内压载荷均匀施加于模型的内表面,同时为了模拟主管与支管管端封闭的情况,把内压作用在端部的效果按式(1)等效为管端的均布拉应力F:
(1)
式中F——主支管的等效均布拉应力,MPa;
P——内压,MPa;
R0——主/支管外径(半径),mm;
Ri——主/支管内径(半径),mm。
材料为ZG30CrMo,材料模型选择理想弹塑性模型,相应的材料性能参数为:弹性模量E=2.05×105MPa,切线模量G=0 MPa,泊松比μ=0.3,屈服强度σy=475 MPa。
1.3 塑性极限载荷的确定方法
有限元分析采用大型通用的ANSYS软件,非线性计算采用修正的Newton-Rapson方法,其优点是具有二阶收敛性,对小挠度和小应变非线性问题能提供精确稳定的分析结果[13]。收敛准则采用力和位移双判据,取最大残余力与最大反作用力之比小于0.005,以保证结果的计算精度。
结构的极限载荷是一个未知量,在有限元分析过程中只能通过施加增量载荷,使结构逐渐达到极限状态,一般采用计算得到的最大载荷或计算至发散时的载荷作为结构的极限载荷。本文选择最后一个稳定收敛的载荷步对应的载荷作为塑性极限载荷。

(2)
式中PL——有限元计算得到的四通塑性极限内压,MPa;
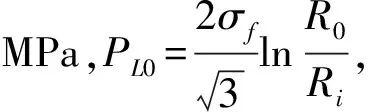
2 尺寸无量纲参数对塑性极限内压的影响
四通的几何尺寸可以用B,A,C及Ptd这4个无量纲参数来表示,其中Ptd是C与A的比值。
2.1 Ptd参数的排除
刘彩霞[9]指出K(可由B变换而来)和Ptd是影响三通塑性极限内压的主要参数,当Ptd为定值时,A,C参数的变化对三通的塑性极限内压数值的影响可以忽略不计,因此在三通研究中可以将A,C参数的影响以Ptd这一中间变量来表示。在进行四通的计算之初参考了这一方法,部分计算结果见表1,分析发现计算结果误差Δ过大,无法用Ptd参数来代替A,C参数的影响,在下面的分析中还需要将A,C这两个参数单独进行考虑。
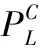
表1 不同几何参量的四通无量纲塑性极限内压
注:Δ=(Max-Min)/Min×100%
2.2 A,C,B参数对塑性极限内压的影响
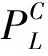
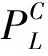

图4 B=10,C=0.5~1.0时,与A的关系曲线
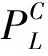
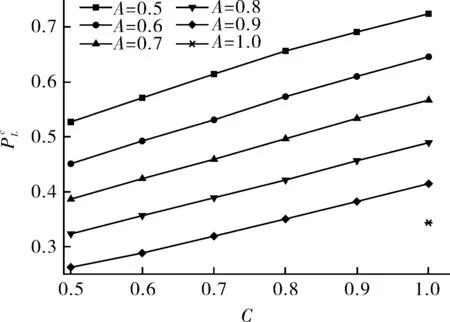
图5 B=25,C=0.5~1.0时,与C的关系曲线
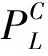
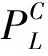

图6 A=0.9,C=0.5~1.0时,与B的关系曲线
2.3 内压作用下四通的失效模式
四通的肩部相贯处是几何不连续区,会形成很大的应力集中,是整个结构最危险的部位。经有限元计算,四通弹性状态下的应力云图见图7,其最大von-Mises应力点出现在内壁的肩部相贯线处,相贯线的腹部也是应力较大的部位。
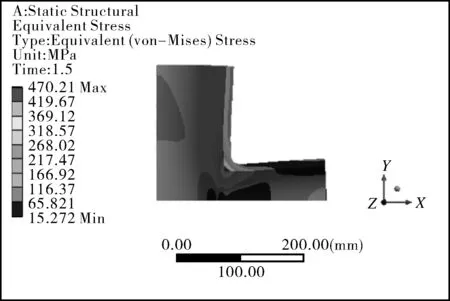
图7 弹性状态下四通应力云图
受内压作用的四通达到极限状态时,其失效模式为相贯区整体塑性垮塌失效,其失效是由于相贯区已全部处于屈服状态,并在相贯线的腹部区域形成了塑性铰(见图8),而远离相贯区的支管端部还处于弹性应力状态。

图8 四通塑性垮塌变形图
3 四通塑性极限内压数据库及拟合公式
3.1 有限元解数据库
如前文给出的计算方案,本文计算了200多个不同参数组合的有限元算例,并将这些算例的结果建立为四通塑性极限内压的有限元解数据库,如表2~7所示。

表2 B=5时的四通无量纲塑性极限内压有限元解

表3 B=10时的四通无量纲塑性极限内压有限元解

表4 B=15时的四通无量纲塑性极限内压有限元解

表5 B=20时的四通无量纲塑性极限内压有限元解

表6 B=25时的四通无量纲塑性极限内压有限元解

表7 B=30时的四通无量纲塑性极限内压有限元解
3.2 四通塑性极限内压拟合公式
根据表2~7中的数据,拟合得到四通无量纲塑性极限内压的估算式:
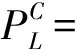
-0.0093B+0.9537
(3)
定义pC为四通削弱系数,pC=0.7443B-0.229C+0.006BA-0.8771A-0.0093B-0.0463。
式(3)可改写为:
(4)
图9为估算公式(4)与表2~7中有限元数据的比较可以看出,不同pC的拟合公式估算值与有限元数值解都十分一致,二者的数值误差最大不超过6%,可见公式(4) 具有很高的计算精度,能够准确地估算焊制四通的塑性极限内压。

图9 估算式(4)与有限元解的比较
3.3 直管、焊制三通及焊制四通的对比

图10 直管、焊制三通及四通的对比关系图
三通、四通与容器接管外形相似,容器接管在一定程度上削弱了容器的承压能力,同样地,三通及四通因支管的存在也会一定程度上削弱主管的承载能力。
以pC为统一自变量,绘制了直管、焊制三通及四通无量纲极限内压与pC的关系见图10。从图中可以看出,pC为定值时,同尺寸的直管、三通及四通的塑性极限内压呈现下降的趋势,支管的存在确实会削弱主管的极限承载能力。
4 结论
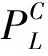

(3)三通及四通因支管的存在也会一定程度上削弱主管的承载能力,同尺寸的直管、三通及四通的塑性极限内压呈现下降的趋势,极限承载能力在逐渐减弱。
