基于恒压激励的伺服式拾振器自校准技术研究

方 翠，郭天太，陈红江，匙庆磊，孔 明

(1.中国计量大学 计量与测试工程学院，浙江 杭州 310018；2.湖南省计量检测研究院,湖南 长沙 410014；3.中国地震局工程力学研究所，黑龙江 哈尔滨 150090)

拾振器作为一种常见的将振动信号转换成电信号的一种传感器，其测量结果的准确性直接影响采集到的振动信号的精度。对于振动与冲击传感器的实验室校准方法，目前已经建立起了一整套的国际和国家标准，也具有较高的校准不确定度，但是现场校准方法的需求却越来越迫切，这是因为大量的传感器被用于长期监测，长期监测的要求使得这些传感器很难被拆除后送至实验室校准，因此发展简单有效的现场校准方法具有现实意义[1]。

拾振器的自校准技术来源于自标定方法，该方法由来已久，在未出现振动台的年代就已经有了广泛的应用。常见的自标定方法有利用内置线圈的自标定方法和重力法静态校准，其中又以内置校准线圈的自标定方法最为常用。在地震观测领域，利用自校准法确定地震计的参数已经形成了一套完整的方法，一般称为电动式标定，其本质是在内置校准线圈中输入指定的信号，根据拾振器的输出响应，确定其参数[2]。

对于内置校准线圈的拾振器的现场自校准，可以采用恒压激励拾振器的校准线圈的校准技术。利用恒压激励拾振器进行自校准，推导出拾振器理论上的自校准传递函数和利用恒压校准技术校准拾振器的传递函数。搭建基于恒压激励的伺服式拾振器自校准装置，通过实验数据说明该自校准方法可以用于伺服式拾振器的自校准。

1 拾振器原理

根据文献[3]，对941型拾振器进行自校准的原理说明，图1是941型拾振器的数学模型，图2是输出电路图。

图1 数学模型Figure 1 Mathematical model

图2 输出电路图Figure 2 Output circuit diagram

941型拾振器属于往复摆式绝对测振仪[5]，其基本原理可用图1的数学模型来描述。运动微分方程为

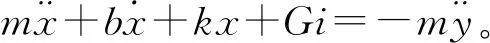
(1)

式(1)中：m为可动质量；b为包括空气阻尼在内的阻尼系数；k为支承导向弹簧刚度；G为传感器测量线圈的机电耦合系数；i为线圈中的电流；y为传感器壳体位移。

电路方程为：

(2)

式(2)中：Rs为测量线圈内阻；e为传感器测量线圈输出电压；C为并联电容；R为并联电阻。

由式(2)得出线圈中的电流i为

(3)

综合式(1)(2)得出电动势e为

推导出

e·Rs(RCs+1)=R(Gsx-e)。

得出电动势e为

(4)

由(1)式推导得出

ms2x+bsx+kx+Gi=-ms2y。

(5)

将(3)式、(4)式带入(5)得

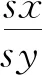
(6)

联合式(4)和(6)得拾振器的灵敏度为

(7)

(8)

(9)

将(9)式代入(7)式得拾振器的灵敏度为

(10)

式(8)中：n为二阶系统的低频固有频率；D为二阶系统的阻尼常数。

2 恒压校准原理

下面分析对拾振器采用恒压校准的原理，恒压校准原理的原理图如图3。

图3 恒压校准原理图Figure 3 Principle diagram of constant pressure calibration

推导过程如下：

(11)

Fexcite=G2·i2。

(12)

式(11)、(12)中：R2为校准线圈内阻；G2为校准线圈机电耦合系数；L2为校准线圈电感；Fexcite为校准线圈所受的激振力。

由(1)、(2)、(8)式得出

(13)

整理得

(14)

结合(3)、(4)式得出线圈中的电流为

(15)

联立(14)、(15)式得

(16)

其中，令

W4=m(R2+L2s)。

(17)

结合(9)、(17)式得

(18)

由(4)、(9)式得

(19)

联立(18)、(19)式得到采用恒压校准的输出电压关于加速度的相对灵敏度，即

(20)

对其分母进行积分后，可得到采用恒压校准的输出电压关于速度的相对灵敏度为

(21)

3 恒压校准实际测试

3.1 恒压校准原理框图

在实际测试中，利用数据处理系统为恒压校准电路提供正弦电信号，其中恒压校准电路的原理如图3，输入的电信号经电压跟随器为拾振器提供校准信号，电压跟随器的输入阻抗很大，而输出阻抗很小，可以用来提高电路带负载的能力。

数字采集系统用来采集拾振器的输出信号，经过数据处理系统，计算拾振器的灵敏度。用恒压激励拾振器的校准原理框图如图4。

图4 恒压校准原理框图Figure 4 Principle block diagram of constant pressure calibration

3.2 试验及数据分析

利用恒压校准装置，对941B型拾振器的速度档进行自校准实验，实验装置见图5。在5个频率点即1 Hz，2 Hz，5 Hz，8 Hz，10 Hz处，分别测量10次，得到速度灵敏度的测量不确定度，如表1。

图5 自校准实验装置图Figure 5 Self-calibration experimental device diagram

从表1的数据可以看出，利用恒压校准装置对941B型伺服式拾振器进行自校准，得到的低频测量不确定度均小于2%。

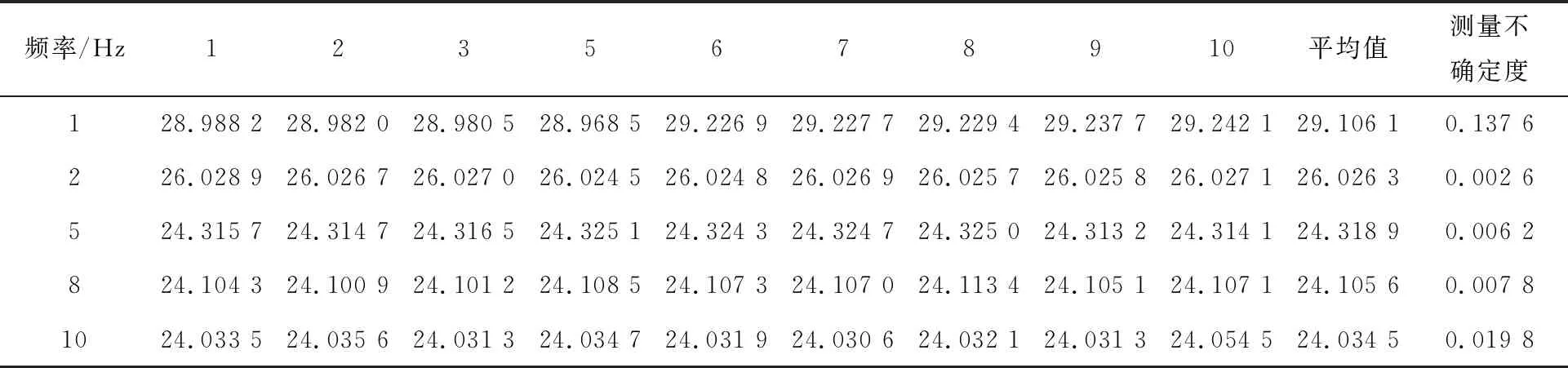
表1 不同频率点的测量不确定度Table 1 Measurement uncertainty of different frequency

此外，为了对比采用恒压法自校准和实验室校准方法的误差，对941B型伺服式拾振器采用标准对比法和激光法校准，得到表2中的数据。

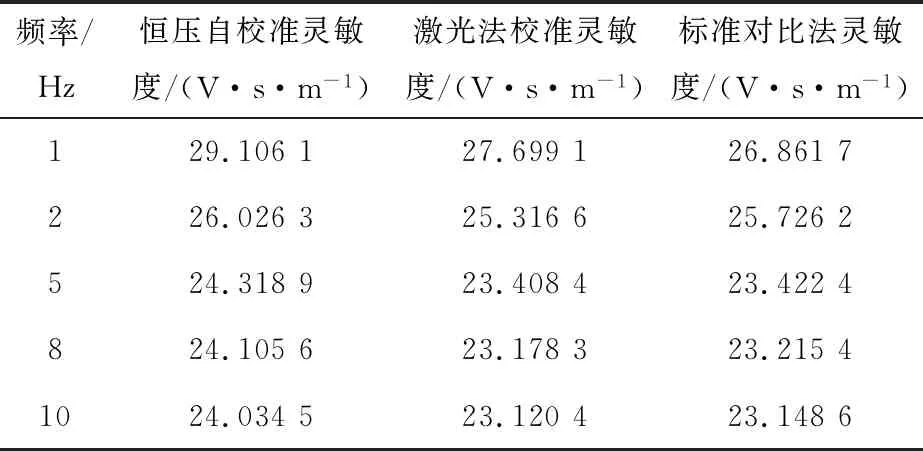
表2 与实验室校准数据对比Table 2 Comparison with laboratory calibration data

为了直观的看出两种校准方法的误差，将它们显示在同一坐标系下，如图6，可以看出对拾振器采用恒压校准的方法与实验室校准方法对比，绝对误差在0.8～2.3之间，且与实验室校准对比，误差变化趋势一致。

图6 不同校准方法的速度灵敏度Figure 6 Velocity sensitivity of different calibration methods

4 结 论

本文结合伺服式拾振器的自校准原理，推导出采用恒压校准技术对拾振器进行自校准的原理。通过搭建的恒压校准装置，对一种典型的伺服式拾振器的速度档进行低频的自校准实验，对同一频率进行多次测量，计算出速度灵敏度的测量不确定度均小于2%，可以用于941B型伺服式拾振器的自校准。此自校准方法便于拾振器的现场自校准，为安装在现场的拾振器的校准提供了一种便捷的方法，此自校准方法也可用于其他种类的带自校准线圈的伺服式拾振器的低频自校准。