从广义虚拟经济视角下的中国房产泡沫增长异质性研究
2019-11-08戴淑庚谢艺菲
戴淑庚 谢艺菲
(厦门大学经济学院金融系 福建 厦门 361005)
一、引言
自20世纪70年代末期以来,虚拟经济在我国经济发展过程中的参与度和重要性都持续增加,不仅引起了广大学者的关注,还被写入党的十六大报告这个纲领性文件中。随着研究的深入,虚拟经济也逐渐被拓展到其广义形式,林左鸣(2010)首次提出了广义虚拟经济的概念,将人的心理需求因素纳入研究范畴,进一步获取除可观测物质之外的重要信息,从而能够对“新”经济现象作出更贴近本质的解释。对比传统意义上的狭义虚拟经济,广义虚拟经济对产业的划分更为丰富,除金融产业之外,还包括旅游,教育等第三产业,甚至渗透了部分实体经济。例如在房地产行业中,参与者的心理需求是影响市场发展的首要因素之一。在2008年次贷危机之后,人们普遍认识到投机性的投资心理导致的楼市泡沫对整个经济体造成的危害。楼市泡沫的破灭或房地产价格的大幅下跌可能导致家庭消费水平大大降低(Case,1992,Skinner,1996,Case等,2005),还可能导致抵押品赎回权的丧失和贷款人的意外损失(Case等,2000),这都将加剧对经济体的负面冲击甚至导致更严重的经济衰退。因此,将广义虚拟经济理论应用到房地产领域,深入研究市场参与者的心理因素,能加深市场管理者对如何对抗投机泡沫的理解。
近年来,中国部分地区房地产价格的大幅上涨备受中国境内外投资者,学者和政策当局的关注。Wu,Gyourko和Deng(2012)发现,中国35个主要城市的实际不变房价是2000年的2.4倍,较2007年第一季度增幅在60%以上;周京奎(2005)发现中国城市房地产市场投机度非常高,价格极大偏离了其长期均衡值。这种非理性繁荣是由人日益增长的心理需求而非实际住房需求所催生的。在中国楼市存在泡沫这一既定事实下,当前的投资者更加关注房地产价格的泡沫增长的变动情况。那么,中国房地产泡沫变动走向如何?这样的变化与投资者预期的价格变动有怎样的关系?还有什么因素决定了房地产泡沫的演化趋势?在当前市场形势下,如何有效利用政策工具进行干预,维护房地产行业平稳健康地发展?这正是本文将研究的问题。本文旨在结合广义虚拟经济视角,测度15年来31个省市及自治区的房地产泡沫变动情况和投资者预期的房价变动情况,并出于对中国地区经济发展不平衡的考虑,将地区异质性纳入考虑,亦即从时空两个维度进行探索,这为如何针对性防范中国房价泡沫风险提供了有意义的研究视角。
二、文献综述
(一)广义虚拟经济
马克思在《资本论》中最早提及了“虚拟资本”这一概念,他定义能产生剩余价值的金融资本为“虚拟资本”,这与早期虚拟经济所特指的金融活动不无关系。后来,人民日益丰富的心理需求和精神需求催生了许多新兴产业,这些产业的发展围绕着虚拟资本,却不再局限于金融产业范畴,从此虚拟经济的范围进一步扩大。林左鸣(2010)将这种虚拟经济形态定义为广义虚拟经济,即“同时满足人的生理需求和心理需求并以心理需求为主导,以及只满足人的心理需求的经济的总和”。自此,广义虚拟经济理论被用于分析各类经济现象,其中针对中国房地产市场的研究成果不在少数。高波等(2013)利用广义虚拟经济的核算方法,发现住宅价格波动不仅影响地产行业,还有非金属矿物制品业等其他关联产业。娄文龙等(2015)认为中国房地产虚拟运行,与实体经济的关系逐渐弱化。田利辉等(2018)利用房价收入比衡量虚拟经济下的房地产泡沫现象,发现城市化水平对泡沫有显著的抑制作用。
广义虚拟经济的本质是人本经济,它将市场参与者的思考和预期纳入研究范畴。正如Kahneman和Tversk(1979)提出的展望理论所述,财富的可能收益和损失会影响经济主体的投资决策。Piazzesi和Schneider(2009)发现往期房地产市场的繁荣将导致家庭对未来房价升值的乐观态度。Lambertini(2013)及Huang(2014)均发现对房价上涨的预期变化对预测房价和其他宏观经济变量的动态变化来说十分重要。Akerlof 和Shiller(2009)认为房地产市场同股市一样,存在羊群效应和动物精神。Baddeley(2005)衡量了房地产成交额与羊群效应、外部效应和市场非理性程度等之间的关系,探究房地产泡沫形成的机理。因此在广义虚拟经济视角下,心理预期是房地产研究的重点。
(二)房地产泡沫
为厘清房地产泡沫的测度逻辑,必须先明确其概念。对泡沫现象的最早的系统性经济研究起始于20世纪70年代左右,Blanchard和Watson(1983)定义了理性泡沫的概念,商品价格可表示为P_t=P^*+b_t,即商品价格可由其基本价值和引起其价格暴涨暴跌的泡沫部分。Stiglitz(1990)最先定义了投机泡沫一词,他认为当投资者对资产未来的价格产生了与经济基本面无关的高预期,并导致了当前的高价格,此时泡沫产生。姜春海(2005)认为,房地产泡沫即投机性预期,由于投资者对未来房价有系统性预期,进而采取群体投机行为,造成房价脱离其基本价值持续上涨。田利辉等(2014)给出了房地产泡沫的“新”解读,认为短期内价格超出基本价值是正常的价格运动,而非泡沫。综上,房地产泡沫是指房价基本价值和市场价格的长期偏离,预期是泡沫的决定性因素。
在此基础上,学者们对中国房地产泡沫的研究主要涉及泡沫的存在,测度及成因。其中,房地产泡沫测度方法主要分为指标法与基准价格比较法。指标法旨在通过构建测量房地产泡沫的社会经济指标体系,确定不同指标的权重,构造出较为综合的指标指数来度量泡沫的大小。丰雷等(2002)利用货币供给和股价指数构建指数体系,测算泡沫的发生概率,时间和程度。刘琳等(2003)采用房价收入比,房价增长率/实际GDP增长率和住房按揭款/居民月收入三个指标构建房地产泡沫测度系数。吕江林(2010)直接将房价收入比用于衡量房地产泡沫,并给出了合理区间。运用指标法度量泡沫的学者众多,在此仅例三。指标法直观易懂,但是由于研究的目标多样,地区经济发展不平衡,学者至今也没有得出一个能够合理衡量房地产泡沫大小的指标,且不同方法之间的可比性也存在很大争议,更重要的是该方法存在混淆景气指标和泡沫测度指标的嫌疑。基准价格比较法则是从定义出发,以理性预期理论为基础,建立商品的基本价值模型,利用市场价格与基本价值的差额定义泡沫,经典案例如Blanchard和Waston(1982)利用套利均衡条件,求解资产的市场基本价值和泡沫。在此基础上,亦有学者针对中国房地产市场进行拓展研究。姜春海(2005)利用消费者期望效用函数,建立优化模型,从而得到房地产基本值并计算投机泡沫。周京奎(2006)在房地产市场局部均衡的框架下,利用投资者决策的博弈思想,得到含有泡沫的房地产市场均衡价格作为基本价值。韩冬梅等(2008)建立商品房供需状态空间模型,将基础价值作为状态变量纳入模型从而计算泡沫。高波等(2014)利用迭代估计了均衡房地产价格的时间序列,进而与市场价格进行比较得到泡沫值。基准价格比较法较指标法而言,定义更为严谨,应用更为灵活。
(三)文献评述
综上可见,学者们对房地产泡沫现象研究的文献众多,但是大部分文献都简单的将投机性泡沫和预期因素决定的部分价格等同起来,并且仅将视角局限于房地产泡沫程度。此外,由于各学者对泡沫程度的测度结果各异,难以确定最精确的测度方法,但是所衡量的泡沫现象趋势大都类似,因此本文认为房地产泡沫增长率是一个优良的切入点。本文的创新点在于:其一,将房价的投机性泡沫和投资者预期因素一分为二,并分别进行建模估计;其二,着眼于增长率,讨论了房地产泡沫的增长情况和投资者预期的房价增长情况,并研究二者的交互作用。
三、实证分析
根据理性泡沫理论,房地产价格由基本价值和价格泡沫构成,姜春海(2005)认为在没有金融中介干预、一般均衡状态下的房价为基本价值,价格泡沫即投机性泡沫;Abraham和Hendershott(1996)根据适应性预期理论建立房地产价格增长率决定模型,利用多次迭代回归求解均衡增长率,同时估计投资者预期成分权重。本文将在以上研究的基础上,将构建面板VAR模型研究投机性泡沫增长率(下文简称为泡沫增长率)和投资者增长性预期成分(下文简称为增长性预期)之间的交互关系。
(一)模型构建
1.投机性泡沫增长率的估计
在没有金融中介干预的市场上,消费者的可支配收入和房地产开发商的自有资金可被视为投资者的预算约束。为正确运用优化模型,本文对消费者和房地产开发商作出如下假定:
(1)房地产市场上的商品房对消费者而言是同质的。
(2)房地产商品价值V=PH和其他商品G构成消费者的总消费,即可支配收入,二者都能为消费者带来效用,其中P为房地产价格,H为房地产消费面积。
(3)消费者效用函数为对数型、加法可分。
(4)消费者各期效用贴现率和房地产开发商各期利润贴现率为1。
(5)房地产开发商对房地产投资资金的机会成本为社会平均收益率R。
(6)房地产建造成本C是建筑面积H的二次函数,以遵从边际递增定律。
(7)消费者可支配收入和房地产开发商自有资金保持不变。
消费者以效用最大化为目标函数,以可支配收入为约束条件,以消费者需求函数为一阶条件:

房地产开发商以利润最大化为目标函数,以自有资金B为约束条件,以房地产开发商供给函数为一阶条件:

联立(1)式、(2)式可得均衡价格表达式为:PS=(EtP(t+i)S。在市场价格处于均衡价格时,消费者效用最大化,边际替代率为dUG/dUV=V/G=1;房地产开发商在第t年的利润为表示投入到房地产中的自有资金获得了社会平均利润。此时可以求得一般竞争均衡条件下的房地产市场价格,即当年房地产商品基本价值为:

但考虑到房地产建设存在一定的时间周期,参照往期文献约为1年,因此,本文将(3)式等号右边的经济变量滞后一期,即今年房地产的基本价值由去年房地产建造成本、社会平均收益和可支配收入决定,则房地产基本价值可表示为:

2.投资者增长性预期成分的提取
在广义虚拟经济视角下,为充分考虑心理预期对房地产价格变动的影响,本文在此利用菲利普的适应性预期理论,认为人们对预期取决于过去的经验,并且利用预期修正当期的行为,即把滞后一期的房价增长率以及滞后一期的房价泡沫引入动态回归模型。这种预期不同于投机性预期,但包括投机性预期,它对房价的影响是双向的:当人们产生投机性预期时,“买涨不买跌”的心理将导致房价上涨时需求增加,房价进一步上涨,反之持续暴跌;当人们产生非投机性预期时,理性经济人将遵从“低买高卖”原则,这样一来是市场便会逐渐稳定。在此,本文的模型延续了Abraham和Hendershott(1996)的建模思路,认为房地产基本价值的增长率为:

其中,cit为房地产建造成本增长率,yit为全体居民人均可支配收入增长率,popit为人口密度增长率,rit为社会平均收益率增长率,iit为房地产开发投资额增长率。
房地产市场价格的增长率为:

其中,et为解释房价增长率的投资者增长性预期成分,可表示为:

即房价增长率中的投资者预期成分可被前一期房价增长率Pt-1以及前一期房价偏离基准价格的程度所表示,εit为随机误差项。这里本文定义λ1为加速系数,若λ1>0,前一期房价增长率升高将导致更高的当期增长率;定义λ2为减速系数,若λ2>0,前一期房价增长率升高将削弱当期增长率(λ1,λ2∈ (0,1))。
综合上述(4)(6)(7)式,房地产价格增长率为:
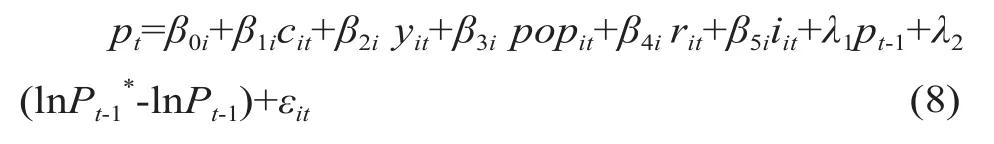
本文称(8)式为预期均衡价格模型,旨在利用房价时间序列实现模型反复迭代,从而得出方程稳态解,从而得到房地产均衡增长率。根据理性泡沫理论,经济基本面要素解释了资产的基本价值,式中的经济要素作为衡量的变量,恰好反映了房地产市场的需求与供给,以及经济基本面对房地产基本价值增长率的解释;滞后变量要素符合适应性预期思想,用来衡量因变量可由预期解释的成分。
(二)数据来源与描述性统计
本文数据来自万德数据库。选取我国31个省级行政单位,包括:北京,天津,上海,重庆,河北,山西,辽宁,吉林,黑龙江,江苏,浙江,安徽,福建,江西,山东,河南,湖北,湖南,广东,海南,四川,贵州,云南,陕西,甘肃,青海,内蒙古,广西,西藏,宁夏,新疆,时间跨度从2002年到2017年,并根据中国四大经济分区划分标准,将以上省级行政单位划分为东部地区,东北地区,中部地区和西部地区,以便研究中国房地产市场异质性。
本文研究所设计的变量及其描述性统计如表1所示。P代表房地产价格(万元),C代表房屋竣工造价(元/平方米),R(%)代表一年期贷款利率,I(万元)代表房地产开发投资额(万元),Y代表全体居民人均可支配收入(元)②,POP代表人口密度(人/平方千米)。从表1来看,各变量值分布分散,说明影响房地产市场的因素在省级行政区之间差异很大,需要进一步通过计量工具进行分析。
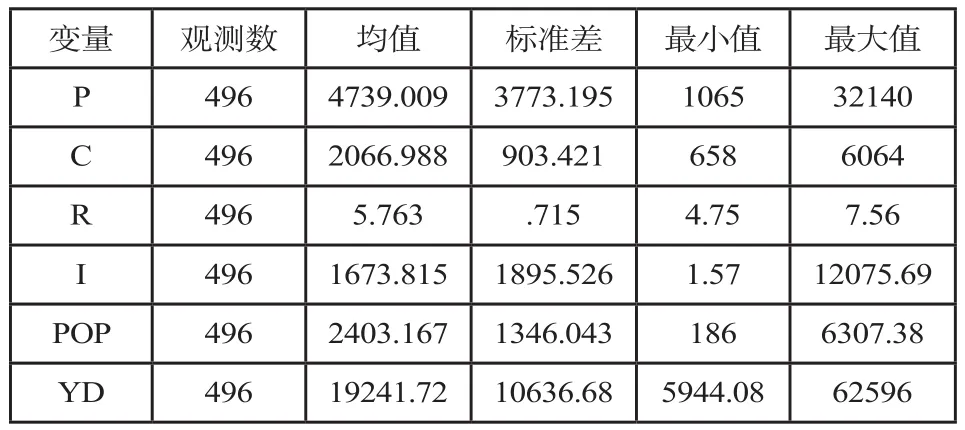
表1 原始变量描述性统计
由于研究模型涵盖了滞后期,为防止非平稳序列的伪回归结果,本文对变量时间序列进行了面板数据IPS单位根检验,其中由于利率是平稳序列,此单位根检验不包括变量R。检验结果如表2所示,各经济变量序列均不稳定,但是一阶差分后均通过了单位根检验,在5%的显著性水平上是平稳的。一阶差分后的各经济变量含义可用增长率解释,符合本文上述模型式(7)构建原理。

表2 时间序列单位根检验结果
(三)实证结果
1.投机性泡沫与房价增长率预期成分的提取
本文在估计投机性泡沫增长率时,考虑到房地产开发商具有夸大建造成本的动机,造成过高的竣工造价观测值,认为实际竣工造价为观测值的90%。而后运用式(4)可得到房地产基本价值、投机性泡沫度bt和泡沫度增长率gbt,各省级行政区的泡沫走势如图1所示。通过折线图初步分析可得,东部省份房地产泡沫程度要明显高于西部省份,中西部的泡沫走势和大小情况类似。

图1 中国31个省级行政单位房地产投机性泡沫走势
在提取增长性预期成分的过程中,由于式(8)中存在未知量不可观测,需要对回归进行迭代处理。本文按照往期文献,处理方法如下:不考虑回归中这一变量,先对回归式进行估计,得出各变量系数,然后将各变量系数带入式(5)估计出。再利用对数形式的增长率公式Pt=lnPt-lnPt-1进行迭代可得:

选定基期为数据时间序列的起始时期,即选取2002年为基期,当期房地产价格记为P0,可求出lnPt-1;在利用上述估计的序列代换Pt,可得和序列将此序列及其他变量带入式(8),便可估计出新系数,从而实现新一轮的迭代。重复以上过程,当方程所估计的系数逐渐收敛后,完成回归估计。本文利用系统GMM计量方法,以将潜在的内生性降到最低,回归结果如表3所示。
经过三次迭代回归,回归系数相差无几,较为稳定,且由于模型包含滞后项,在迭代回归的过程中每迭代一次便损失一个自由度,为保证时间序列估计的可信度,本文迭代止于此。在估计过程中,AR(1)和AR(2)统计量表明,模型一阶序列存在自相关,二阶序列不存在自相关;Hansenp统计量表明结果不存在工具变量过度识别的问题,可见回归拟合良好。
观察回归系数可得:一方面,在构成经济基本面的变量中,房地产价格增长率与房屋竣工造价增长率,全体居民人均可支配收入增长率和房地产开发投资额增长率呈正向关系,这一结果符合普遍预期;房价增长率与贷款利率增长率同样呈正向关系,本文认为当贷款利率增长速度加快,代表着投资者购房成本增长速度加快,因此投资者为了避免未来付出的高购房成本,当期购房需求将会加速增长,从而推动房价增长率的提高。另一方面,在表示增长性预期的变量系数中,加速系数λ1为负,减速系数λ2为正,且 |λ1|>|λ2|,二者的协同作用表明,房地产价格增长率有很强的自我调节能力,即前一期房价的高速增长将抑制当期房价增长率,反之将促成当期的高房价增长率。本文认为其中的逻辑为:投资者对房价增长率的预期不同于对房价的预期,当房价上涨,人们认为价格还有进一步上涨的可能,进而购房需求增加;然而,当房价增长率处于高位时,人们出于对边际递减规律的认识,认为价格的变化幅度会降低,即增长率下降,反之,当房价增长率处于低位时,人们出于对边际递增规律的认识,认为价格变化幅度会增加,即增长率上升。
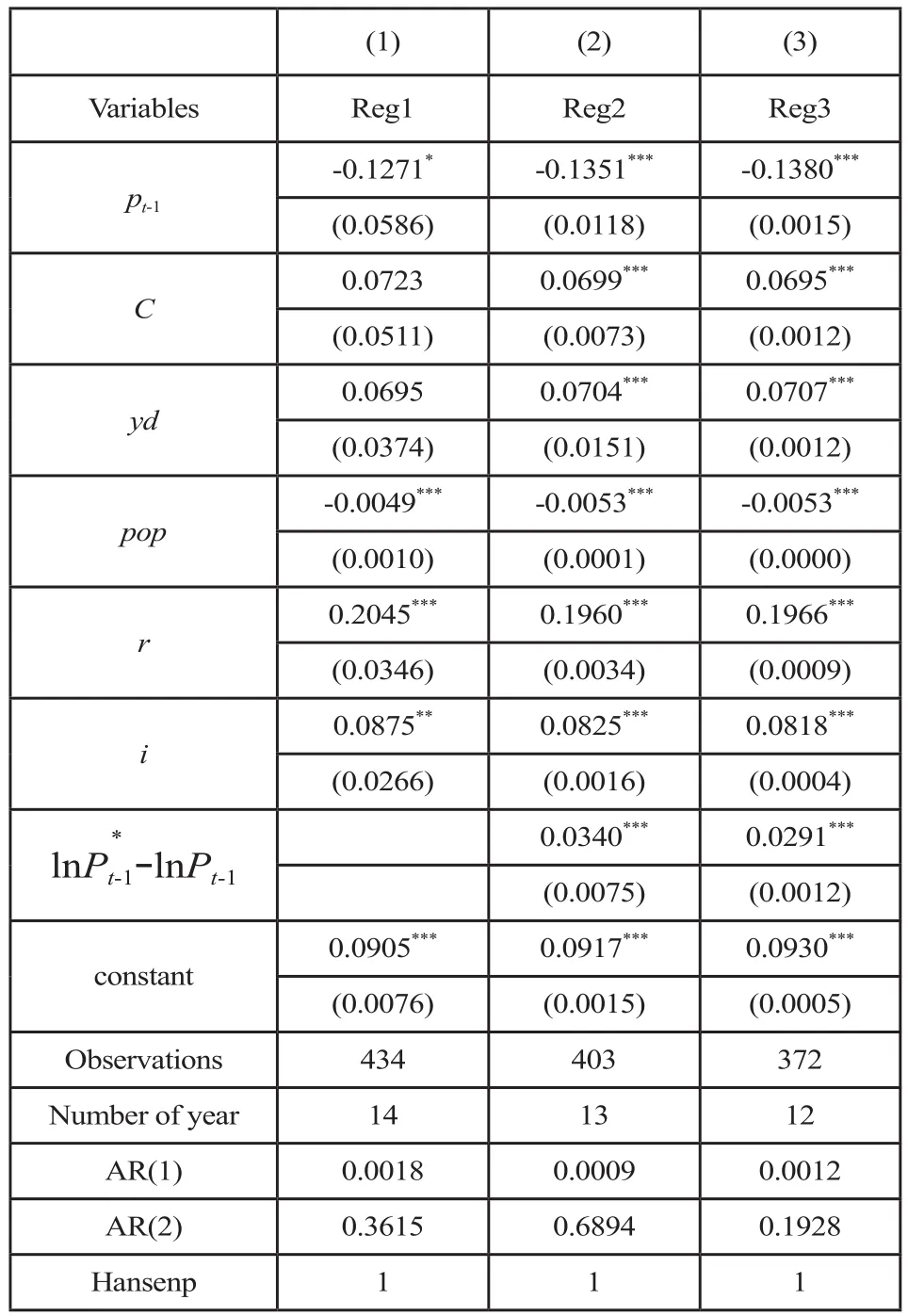
表3 系统GMM迭代回归结果

图2 中国31个省级行政单位房地产增速预期成分走势
以上回归中各变量系数可看作解释因变量的各成分的权重,因此本文根据提取出方程中的预期成分,记为 :et=λ1pt-1+λ2(lnPt-1-lnPt-1),具体情形如图2所示。从图中可以观察到,各地区房地产增速中预期成分的走势各异,波动巨大,难以分析,但大部分省级行政单位在多数年份的预期成分都为负数,说明我国房地产市场对房价增长率的预期大多为负向,即房价上涨正在逐步减速,侧面也说明了我国各地区房价增长率大多还居于高位。
2.面板VAR模型构建
为进一步分析泡沫增长率gbt与增长性预期et的交互影响关系,本文将设置二者为内生变量,基于面板VAR模型,利用其格兰杰因果检验,脉冲响应函数及方差分解工具,探究二者的动态关系。VAR模型如下所示:

其中,i代表省份个体,t代表时间,n代表滞后阶数,yit=[gbt,et]'。变量确定完成后,本文对泡沫增长率与增长性预期进行平稳性检验,二者均通过了单位根检验,如表4所示。为进一步确定模型中两个变量的滞后阶数,本文利用AIC信息准则,在5%的显著性水平下,选取3作为模型的滞后阶数,如表5所示。
表4 面板VAR单位根检验

表5 面板VAR滞后阶数选择
格兰杰因果检验利用VAR模型判断变量间的相互影响的因果关系。下面检验泡沫增长率gbt与增长性预期et之间是否存在格兰杰因果关系,结果如表6所示。可以看出,在5%的显著性水平下,不能拒绝“et不是gbt的格兰杰原因”的原假设,因此不能得出增长性预期是泡沫增长率的格兰杰原因,但在10%的显著性水平下结论相反;但能够拒绝“gbt不是et的格兰杰原因”的原假设,因此可以得出泡沫增长率是增长性预期的格兰杰原因。换言之,一方面投资者预期的变化会影响房地产市场泡沫增长的快慢程度,使得泡沫的产生增速或减速,但是影响并不是非常显著;另一方面,房地产市场泡沫增速能显著影响投资者对于房价增长率的预期,使得预期更为乐观或悲观。二者的交互影响关系形成恶性循环,进一步扩大房地产市场价格的不稳定性,加剧其对经济的负面冲击。
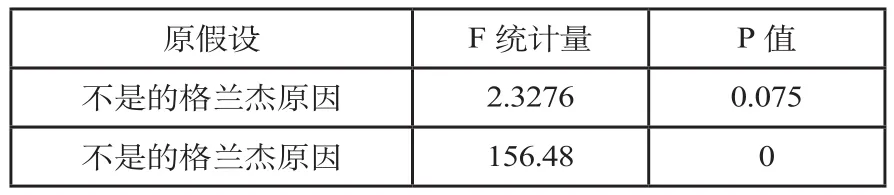
表6 格兰杰因果关系分析
脉冲响应分析可用来考察变量间随时间的动态影响关系,本文将通过这一工具分析当给一变量一单位正向冲击时,另一变量随时间推移的路径变化。为考察中国房地产市场地区异质性,本文按照《中国统计年鉴》中国四大经济区域划分,依据东北振兴、中部崛起、西部开发和东部率先发展的主要内容,将样本中31个省级行政单位划分为东北地区,东部地区,中部地区和西部地区③,由此利用脉冲响应函数讨论增长性预期对泡沫增长率的脉冲响应和地区差异。
中国31个省级行政单位泡沫增长率和增长性预期之间的动态关系如图3所示,当投资者增长性预期受到一个正向冲击后,泡沫增长率出现明显的正向反应,在第二期达到最大,而后迅速下降并随时间推移响应消失;当泡沫增长率受到一个正向冲击后,增长性预期出现明显的负向反应,在第一期达到最大,而后迅速回升逐渐平缓。该现象的发生可被解释为:外部条件对投资者增长性预期正冲击将导致正向适应性预期,市场投资者集体追涨杀跌,从而泡沫加速增长;对增长性预期的正向冲击将导致预期的高增长购房成本,市场投资者对价格大多保留观望态度,从而对泡沫增长率产生负面影响,而一旦泡沫增速放缓,投资者预期反向调整,而后泡沫增长率恢复。以上变化的影响在长期内将逐渐收敛为零。

图3 中国31个省级行政单位脉冲响应分析(左图为gbt对et的响应,右图为et对gbt的响应,下同)

图4 东北地区脉冲响应分析
东北地区房地产市场泡沫增长率与增长性预期的脉冲响应结果如图4所示。从结果来看,泡沫增长率对增长性预期冲击的响应为正向显著,但在第三期出现了负向冲击,说明房价持续且快速走高后,出现热度褪去泡沫增长率回落的现象。增长性预期对泡沫增长率冲击的响应为负向显著,但冲击的收敛并没有整体房地产市场迅速,说明东北地区泡沫增速调整较全国市场稍稍缓慢。
东部地区与西部地区房地产市场泡沫增长率与增长性预期的脉冲响应结果如图5和图6所示,较之中国31个省级行政单位,冲击方向的结论基本一致。通过观察冲击程度可以发现,在东部地区泡沫增长率与增长性预期的交互作用显著高于西部地区,说明我国东部地区的房地产市场更容易受到投资者预期的影响,泡沫的增长也更容易影响投资者预期,这也侧面印证了东部地区市场较于西部地区更不稳定。
中部地区房地产市场泡沫增长率与增长性预期的脉冲响应结果如图7所示。从图中可以观察到,中部地区泡沫增长率对增长性预期冲击的响应短期内为负,长期回正,说明在中部地区房地产市场中,投资者短期的投资态度较为理性,即房价泡沫增长率上升时,投资者认为房价上涨的幅度会回落,之后随时间推移逐渐调整增长性预期。增长性预期对泡沫增长率冲击的响应为负向显著,与全国其他各地区类似。

图5 东部地区脉冲响应分析
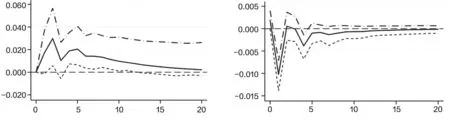
图6 西部地区脉冲响应分析

图7 中部地区脉冲响应分析
可以看出,中国各省级行政单位房地产泡沫增长率与预期有着密切的关系,但是影响程度在区域之间存在一定的差异。其中值得一提的是,东部地区房地产市场最不稳定,市场对预期的影响程度高,冲击速度快,反之亦然;中部地区投资者增长性预期较为理性,具有稳定市场的作用。
从以上因果分析和脉冲响应分析可得泡沫增长率和增长性预期的动态影响程度,但这是否能严格解释变量时间序列的波动情况需要进一步使用方差分解进行分析,表7报告了对变量标准差的冲击产生的交互影响,展示了冲击产生后10期的结果。从对增长性预期的解释程度来看,除了第一期其自身解释能力最强以外,其他时期的自身解释能力仅接近50%。对比而言,泡沫增长率的自身解释能力强大许多,到第10期依然能保持90.8%的水平,说明泡沫增长率惯性大。进一步印证了格兰杰因果检验的结果:泡沫增长率是增长性预期的格兰杰原因,且这一结论显著,反之弱显著。
综上所述,本文认为泡沫增长率和增长性预期互为格兰杰因果关系,脉冲响应分析显示在中国各地区中二者的动态影响存在一定差异,方差分解结果说明泡沫增长率的波动主要由自身解释,而投资者增长性预期中有很大的成分由泡沫增长率解释。因此,在讨论中国房地产市场增长情况的视角下,将预期成分纳入考虑是明智之举。

表7 方差分解分析
四、结论与政策建议
本文在广义虚拟经济视角下,根据理性泡沫理论和动态均衡思想,提取中国各地区房地产泡沫增长率和投资者增长性预期,分析房地产市场异质性。本文实证分析表明,从时间来看,中国31个省级行政单位自2002年到2017年房地产泡沫均在上升,在2010年房价泡沫势头达到相对高峰,所有样本单位的房地产泡沫走势相当,幅度各异。从空间来看,东部地区房地产泡沫较大,且增长率与投资者预期交互作用强,市场波动性强,容易发生暴涨暴跌现象;中部地区房地产泡沫低,投资者对房价增长率的预期成分较为理性,有助于形成健康的房地产市场状态;东北地区与西部地区房地产市场情况适中,但也存在价格泡沫现象,投资者预期中存在一定的不理性成分,可以看出,基于广义虚拟经济,我国房地产市场表现出显著的异质性。
出于上述分析与结论,本文认为房地产泡沫的治理,必须与投资者预期相结合,采取综合性的措施:其一,政策制定者应充分考虑房地产投资者,包括消费者和房地产开发商等各方的利益,帮助各方获取充足信息,积极引导投资者预期,使市场信息与投资者预期同步,进而减少市场信息不对称,催生房地产中介的错误引导而造成的非理性行为。其二,制定硬性政策约束投机者行为,从制度层面出发,对房地产泡沫进行干预,如开征财产税增加投资性购房成本;控制按揭贷款条件与风险,谨慎加息;设置首付比例阶梯制度等。其三,根据中国房地产市场发展异质性,针对地进行市场宏观调控,适度控制房地产泡沫,循序渐进,保证中国各地区房地产市场在长期平稳健康地发展。
注释:
① 与姜春海(2005)定义不同的是,本文允许投机性泡沫为负。
② 由于数据缺失,在此采用的数据为城镇居民人均可支配收入的0.7倍
③ 东北地区:辽宁省、吉林省、黑龙江省;东部地区:北京市、天津市、河北省、上海市、江苏省、浙江省、福建省、山东省、广东省、海南省;中部地区:山西省、安徽省、江西省、河南省、湖北省、湖南省;西部地区:内蒙古自治区、广西壮族自治区、重庆市、四川省、贵州省、云南省、西藏自治区、陕西省、甘肃省、青海省、宁夏回族自治区、新疆维吾尔自治区
