Uncertain Knowledge Reasoning Based on the Fuzzy Multi Entity Bayesian Networks

Dun Li,Hong Wu,Jinzhu Gao,Zhuoyun Liu,Lun Li and Zhiyun Zheng,

Abstract:With the rapid development of the semantic web and the ever-growing size of uncertain data,representing and reasoning uncertain information has become a great challenge for the semantic web application developers.In this paper,we present a novel reasoning framework based on the representation of fuzzy PR-OWL.Firstly,the paper gives an overview of the previous research work on uncertainty knowledge representation and reasoning,incorporates Ontology into the fuzzy Multi Entity Bayesian Networks theory,and introduces fuzzy PR-OWL,an Ontology language based on OWL2.Fuzzy PROWL describes fuzzy semantics and uncertain relations and gives grammatical definition and semantic interpretation.Secondly,the paper explains the integration of the Fuzzy Probability theory and the Belief Propagation algorithm.The influencing factors of fuzzy rules are added to the belief that is propagated between the nodes to create a reasoning framework based on fuzzy PR-OWL.After that,the reasoning process,including the SSFBN structure algorithm,data fuzzification,reasoning of fuzzy rules,and fuzzy belief propagation,is scheduled.Finally,compared with the classical algorithm from the aspect of accuracy and time complexity,our uncertain data representation and reasoning method has higher accuracy without significantly increasing time complexity,which proves the feasibility and validity of our solution to represent and reason uncertain information.

Keywords:Ontology language,uncertainty representation,uncertainty reasoning,fuzzy multi entity Bayesian networks,belief propagation algorithm,fuzzy PR-OWL.

1 Introduction

Data acquisition technology,storage technology and computer performance have gained rapid development in the information era,and the global data size is doubled every 20 months.Moreover,data not only are big in volume,but also involve increasingly diversified types as well as complicated and changeable data relations.In order to make the computer automatically process and integrate valuable data in network,the semantic web is proposed.

The increasing popularity of semantic web services makes it a challenging task to represent and reason uncertain data.However,the existing theory and practices do not provide enough feasible solutions to deal with the uncertainty of semantic web.To some extent,semantic markup languages,such as OWL(Ontology Web Language)or RDF(Resource Described Frame),can be used to signify the quality and quantity information of uncertainty,but they still have limitations.Previously proposed solutions include Probabilistic and Dempster-Shafer Models and Fuzzy and Possibilistic Models.BN and MEBN are two representative models based on probability and the corresponding ontology languages are OntoBayes based on BN[Yang(2007);Yang and Calmet(2006)],BayesOWL[Ding,Peng and Pan(2006)],and PR-OWL2 based on MEBN[Costa Laskey and Laskey(2008);Carvalho,Laskey and Costa(2013)],major ontology languages based on fuzzy model such as Fuzzy OWL[Calegari and Ciucci(2007)],etc.The existing uncertainty ontology languages cannot represent and reason probability and fuzzy information at the same time.

Fuzzy Multi Entity Bayesian Networks(MEBN)[Golestan,Karray and Kamel(2013,2014)]was proposed to represent the fuzzy semantic and uncertainty relation between knowledge entities.This paper aims to extend the expression and reasoning ability of ontology for fuzzy probability knowledge and propose a method to denote and reason uncertainty.

Based on the ontology language,Fuzzy PR-OWL of Multi Entity Bayesian Networks,in this paper,we propose a novel reasoning method of fuzzy probability according to Fuzzy MEBN.Our main contributions are as follows:

(1)The fuzzy probability ontology of Fuzzy PR-OWL is created;

(2)Through integrating the fuzzy probability theory and Bayesian network,the reasoning framework of Fuzzy PR-OWL is created and the reasoning method of fuzzy Belief Propagation are proposed;

(3)Experimental results prove the feasibility and validity of our proposed reasoning method.

2 Relevant theories

2.1 Fuzzy set and fuzzy probability system

Fuzzy set is a kind of description about fuzzy concept,which originates from the uncertainty and inaccuracy essence of abstract thought and concept,rather than the randomness of set elements.The logical value of fuzzy logic can be expressed with a real value in[0,1],which is the multivalued logic of fuzzy set.The fuzzy set theory transfers logical reasoning from two-valued logic into multivalued logic for predictive reasoning.

Zadeh[Zadeh(1968)]defined the probability of fuzzy event by extending the classical theory of probability.Suppose thatxis the random variable in the sample spaceXandAis the subset that defines discrete events inX.The non-conditional probability ofAcan be calculated by Eq.(1):

whereXA(x)is the binary characteristic function,that is,and.

In fuzzy events,the characteristic function is the membership degree function.By replacingXA(x)in Eq.(3)with the membership degree functionμA(x):x∈[0,1],we can calculate the probability of fuzzy events.Berg et al.[Berg,Kaymak and Rui(2013)]calculated the probability of fuzzy eventAusing Eq.(2):

And the probability of fuzzy discrete eventAcan be calculated by Eq.(3):

wheref(x)is the probability density function of variablexandμ(x)is its membership degree function.Eq.(3)assumes that the conditional probability density function is correlated withμ(x).

Suppose thatAc(c=1,…,C)is an event in sample spaceX,and each discrete sample belongs to one or zero event.If a samplexhas a group of membership degreesμA1,μA2,…,μAc,xis considered a fuzzy sample.To ensure the validity of probability theory,a good sample space is expected to meet the following condition:

2.2 BN and MEBN

Bayesian Networks(BN)[Heckerman(1997)]can deal with uncertain and probabilistic events according to the causal relationship of events or other relationships,and has the ability to process incomplete datasets,but BN has limitations when representing entity relationships.Fig.1(a)shows relevant knowledge of tracheitis represented by BN.Tracheitis can be triggered by either smoking or getting cold can in turn be triggered by weather factors.The causal relationship can be clearly seen in the Fig.1,but BN cannot show the influence of harmful gases produced by others' smoking behavior on the patients.Multi Entity Bayesian Networks(MEBN)[Chantas,Kitsikidis and Nikolopoulos(2014)]adopts the idea of “processing by division” by representing knowledge blocks with multientity fragments and then using multi-entity rules to link these fragments together.Fig.1(b)shows relevant information of tracheitis represented by MEBN.Inherent nodes,input nodes,and context nodes are indicated by ovals,trapezoids,and pentagons,respectively.otherandpersonare both examples ofPersontype.other=peopleAround(person)means thatotheris the neighbor toperson.In this way,MEBN can show the relationship between the entities as well as the influence of others' smoking on the patient's bronchitis by adding the nodeSmoke(other).

However,human experience or knowledge is fuzzy by nature and therefore cannot be handled by MEBN.As shown in the above example,severeness of cold may affect the probability of suffering tracheitis.But MEBN can only use 0 or 1 to represent the possibility of suffering cold.In addition,when an inherent node has a nominal value,MEBN would assign equal probability to all nominal scales.For example,suppose that the weather today has two possible nominal scales,clear or cloudy,MEBN would assign the probability value 0.5 to both scales.It fails when the weather is partially cloudy.

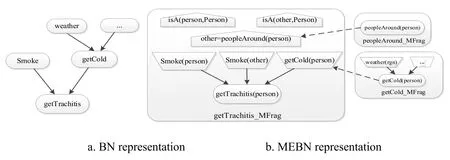
Figure 1:BN and MEBN Representation graph of bronchitis etiology

2.3 Fuzzy MEBN and fuzzy PR-OWL

2.3.1 Fuzzy MEBN

Fuzzy Multi Entity Bayesian Networks(Fuzzy MEBN)redefines the grammar specification by combining the first-order logic and the fuzzy MEBN theory,allowing the context constraints of MEBN to express the fuzziness of incomplete semantic information[Zheng,Liu and Li(2016)].Hence,the expression and reasoning ability of inexact knowledge is improved.Therefore,fuzzy MEBN can represent fuzzy information that cannot be expressed with MEBN in Subsection 1.2,such asMild Cold{true0.3 1,false0.7 0},in which subscripts denote severeness of cold.Partiallycloudcan then be represented by{clear0.6 0.5,cloudy0.4 0.5},in which subscripts denote the membership degree.

Fuzzy MEBN conducts modeling for specific domain ontology with the predefined attribute entity,semantics and their relationships.The attribute entity is represented by constant elements of a specific domain,and the variables are associated.The entities and relationships between entities are represented by logical and random variables of specific domain.As for the biggest difference between fuzzy MEBN and MEBN in entity and random variable symbol,the membership degree of a real number between 0 and 1 is added to the constant element symbol and entity identifier as subscript,such asVehicle0.85and!V 4280.75.The logic or value taking of random variable is the logical value in logical value chainL=＜l1,l2,l3,...,ln ＞predefined by the language or within the scope of[0,1],rather than simpleTorF.

The basic model of fuzzy MEBN is similar to that of MEBN.In fuzzy MEBN theory,the probability distribution is denoted by Fuzzy MEBN Fragments(FMFrag).The inherent random variable or input random variable value is set as the condition,and oneFMFragwill define one probability distribution or several fuzzy rules for inherent random variable.The formalized definition of FuzzyMFrag(FMFrag)isF=(C,I,R,G,D,S),where Cis the infinite set of context random variables,Irepresents the infinite set of input random variables,Rindicates the infinite set of inherent random variables,Grepresents the directed loop-free fragment graph,comprised of variable nodes inI∪R,Dmeans the local distribution of every inherent random variable inR,andSdenotes the set of fuzzy if-then rule used by fuzzy reasoning system.Context variables contain the semantic structure of knowledge that adopts fuzzy first-order logic.As the bridge with other inherent variables ofFMFlags,input variables will send relevant information to the currentFMFrag.Inherent variables is random variables that set the values of context and input variables as conditions.The setsC,IandRhave no intersection,and the random variable inIis the root node of fragment graphG.The context assignment item inCis used to strengthen the constraint of local distribution.

InFMFrags,the context constraint is endowed with a true value,representing the degree of satisfying constraint.The consistency constraint degree ofFMFragsis determined by the fuzzy explanation of the item defined byFMFragand built-inFMFrags.When a common random variable is associated with an internal node,the aggregation function and the merging rule would be used.

2.3.2 Fuzzy PR-OWL

Fuzzy PR-OWL ontology adopted OWL2 DL language to define ontology class and attribute.In other words,OWL2 language is used to describe elements like classes and subclasses obtained from fuzzy MEBN concept abstraction.For instance,declaration node class(Node)can be expressed as function Declaration(Class(:Node)),and it represents the entity and random variable of fuzzy MEBN.Fig.2 shows Fuzzy PR-OWL ontology language(relation between classes and sub-classes)created with Protégé.Fuzzy PR-OWL ontology is based on fuzzy MEBN,and relevant classes and attributes of concepts like fuzzy random variable,fuzzy state,membership degree,and fuzzy rule are added based on PR-OWL2,to enhance the expressive force of uncertainty information.

Figure 2:Fuzzy PR-OWL ontology elements

The basic model of Fuzzy PR-OWL is presented in Fig.3,in which each piece of probability ontology has at least oneFMTheorytype,namely a label.It connects one group ofFMFragsto form an effectiveFMTheory.In Fuzzy PR-OWL grammar,the object attributehasFMFragis used to represent the connection.FMFragis composed of multiple nodes,and each node type is a random variable.The biggest difference between Fuzzy PROWL and PR-OWL2 is,when the fuzzy state of random variable node is defined,the set of fuzzy rule reflecting the state of domain expert is used to define the membership degree of fuzzy state,and the object attributehasFRSconnects each node to one or several fuzzy rule sets.The non-conditional or conditional probability distribution is represented with the classProbabilityDistribution,and is connected to their own nodes through the object attributehasProbDist.The object attributehasFMExpressionconnects every node to a logic expression or simple expression based on fuzzy first-order logic.

Figure 3:Basic model of Fuzzy PR-OWL

3 Reasoning based on fuzzy PR-OWL ontology

3.1 Reasoning framework

This section presents the fuzzy probability reasoning method based on Fuzzy PR-OWL ontology of fuzzy MEBN.Data fuzzification is first conducted and Situation-Specific Fuzzy Bayesian Network(SSFBN)of fuzzy MEBN is constructed.Then,fuzzy belief propagation based on fuzzy rule reasoning is conducted on the constructed network.The reasoning framework of Fuzzy PR-OWL ontology is mainly composed of four basic modules(as shown in Fig.4),including ontology analysis and memory module,data manipulation module,reasoning module,and representation module.

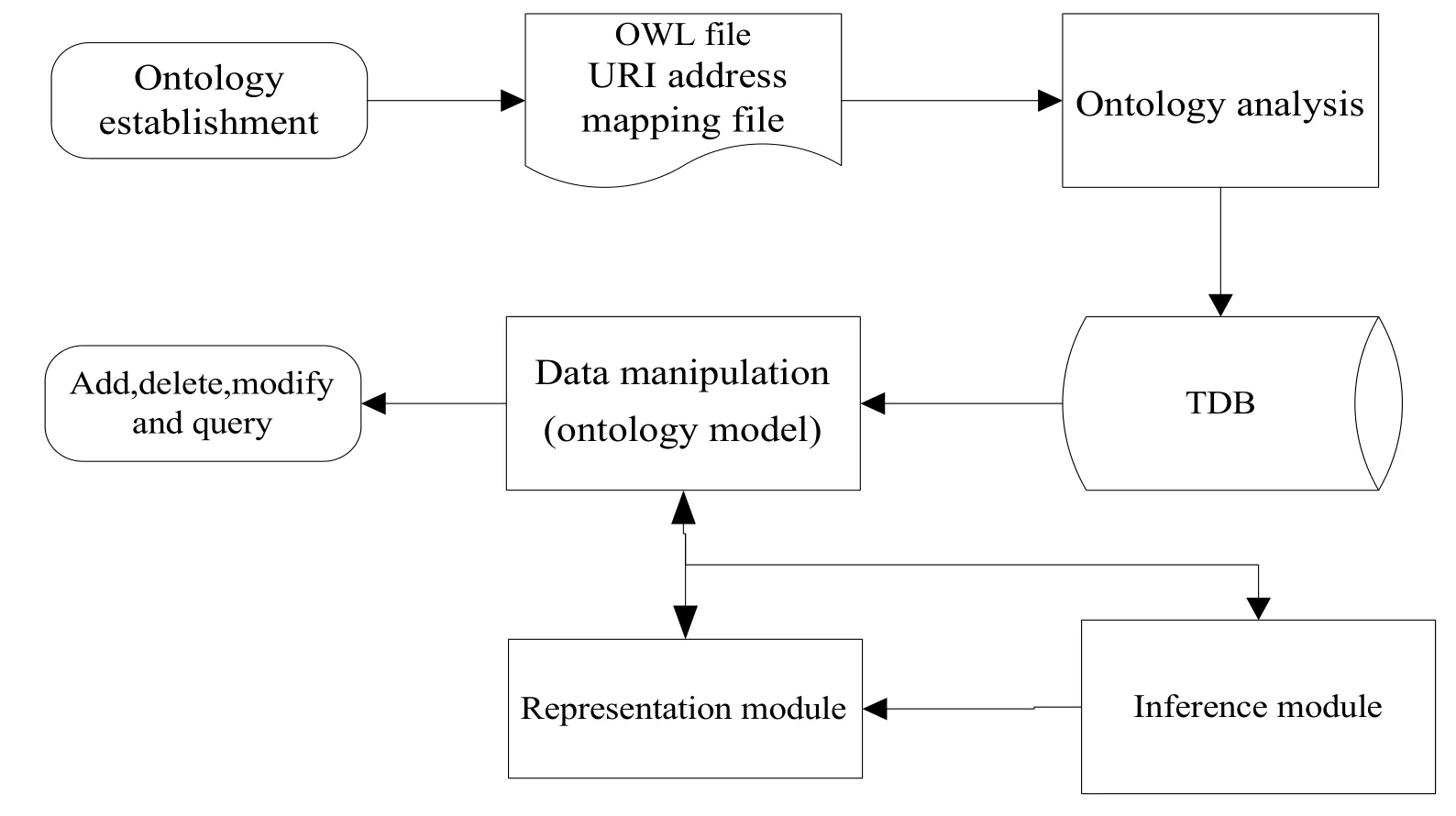
Figure 4:Reasoning framework diagram of Fuzzy PR-OWL

(1)Ontology analysis and TDB memory module

Ontology analysis and TDB memory module is realized based on Jena API.It reads,analyzes the ontology constructed by Protégé,and stores it in the RDF database of Jena[Noy,Fergerson and Musen(2000)].The program first realizes the mapping between ontology URI and the corresponding ontology module file system address through URI address mapping file,and then reads various ontology module files via Java program or configuration files of Jena.In addition,data persistence is conducted in the RDF dataset.A built-in storage mode TDB officially recommended by Jena is used by memory module[Owens,Seaborne and Gibbins(2008)].Characterized by fast reading speed and simple operation,this module can store billions of records at most,and support hundreds of parallel queries.Hence,it is quite suitable for the demand of ontology reasoning.

(2)Data manipulation module

Data manipulation module implements the adding,deletion,modification and querying operations by utilizing the query operation interface of TDB.The module maps the loaded TDB model to corresponding Java ontology or examples.Moreover,by integrating adding,deletion,modification and querying operations through the ontology statement of the TDB dataset,Java ontology implements RDF database operations through TDB operation interface.

(3)Reasoning module

Reasoning module contains an implementation of the Belief Propagation reasoning algorithm[Shafer and Shenoy(1990)]based on fuzzy probability.Both FuzzyOWL reasoning engine and API of UnBbayes[Carvalho,Laskey and Costa(2010)]framework is used,and reasoning and querying can be conducted on specific nodes.Specifically speaking,it can handle knowledge base loading,fuzzy processing of data,SSFBN construction,and fuzzy probability reasoning functions.

(4)Representation module

Representation module handles GUI.It can manipulate the database through the graphical user interface,and display data variation in the database and reasoning results produced by the reasoning module.

3.2 Belief propagation algorithm based on fuzzy probability

In order to construct a Situation-Specific Bayesian Network(SSBN)based on knowledge and produce the minimum Bayesian network responding to query,common MEBN first sets prior distribution of target random variable and evidence random variable(also known as discovery random variable)as the condition.Then,posteriori distribution of target variable is reasoned through running the classic Bayesian network algorithm.

3.2.1 Data fuzzification

The algorithm proposed in this paper requires preprocessing the fuzzy concept or natural language variable gained from expert knowledge before establishing SSBN,so as to obtain the membership degree of fuzzy state of the variable.Some symbols and connotations involved in the algorithm need to be defined first.

Definition 1:the set of entity identifiers.In FMFragF,the local node(or random variable)ψ(θ)has a set Nψcomposed offuzzy states,and the corresponding fuzzy set isA.Then:

(1)f(μA,α)=(μA)α,in which μAis the membership degree function of setA,that is μA:U →[0,1];α∈[0,1]is the fuzzy factor.The functionfis a general form of the fuzzy theory.

(2)The fuzzy state of ψ can be denoted by,in whichε,and αirepresents the membership degree of stateis the membership degree vector of ψ.

(3)The probability distribution vector corresponding to CPT of ψ is denoted by πψ=

In FMFragF,the local node ψ has multiple fuzzy states.For instance,if “height” is set as a random variable,there are three states(“short,medium,high”).“The person is relatively high” can be denoted by the fuzzy state ＜short0,medium0.2,high0.8＞.

Random variables are discrete variables,and the membership degree of fuzzy state of these random variables should be obtained through fuzzification and discretization.The method to calculate the membership degree of fuzzy state of random variables mainly depends on the type of expert data(as shown in Fig.5):

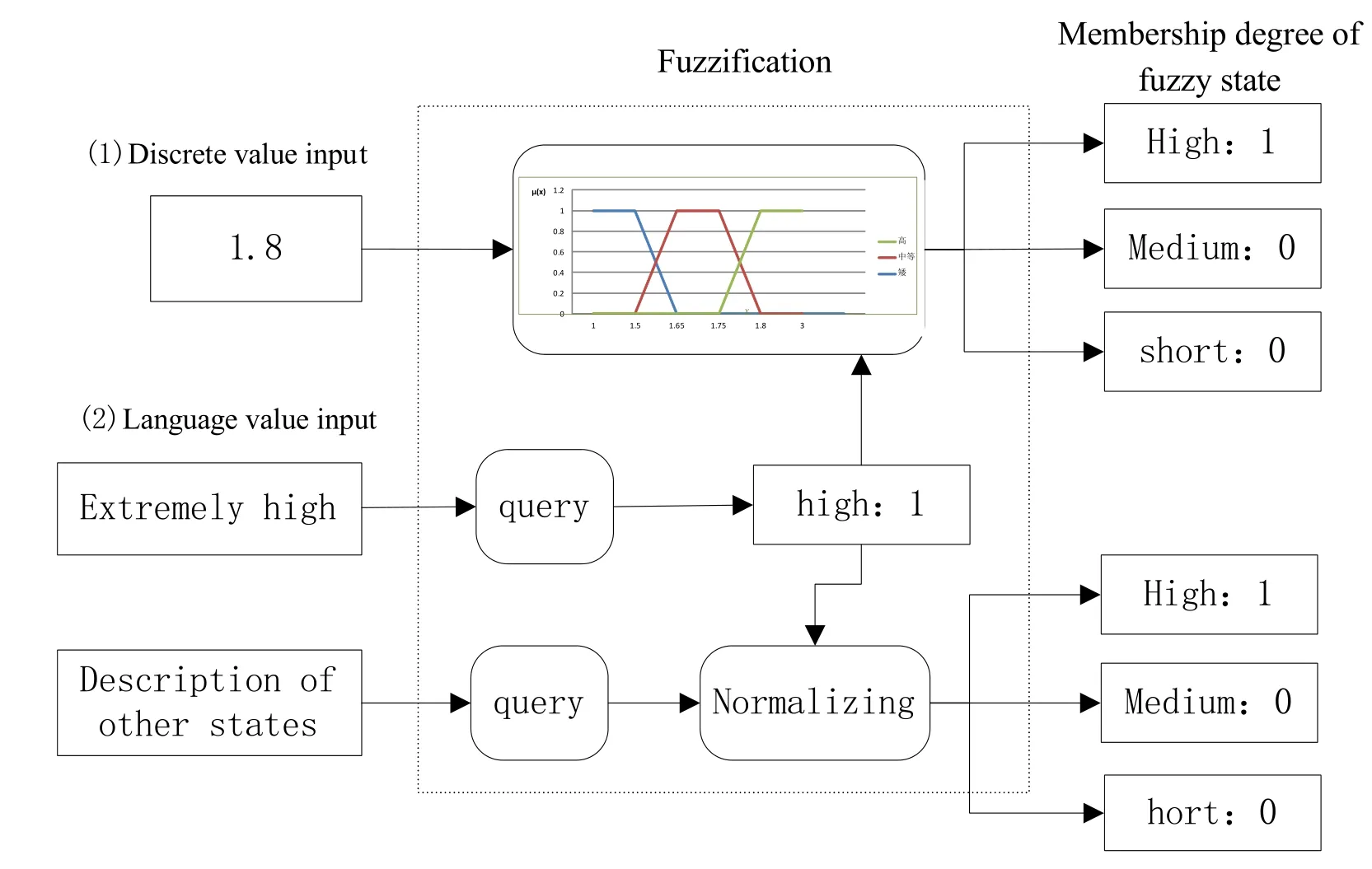
Figure 5:Schematic diagram of data fuzzification

(1)Discrete value input

As the specific data x∈U is known,the membership degree can be calculated through the membership degree function μAi(x)(retain one digit after the decimal place).For instance,the height 1.8 can be substituted into membership degree functionμshort(x),μmedium(x),μhigh(x)defined in the domain of discourse[1.0,3.0],to determine the membership degree.

(2)Language value input

As the language's descriptor is known,the membership degree interval of corresponding extent description language variable can be determined using Tab.1.Created from researches on degree adverbs of modern Chinese language and the division of Vasilios et al.for degree in English[Carvalho,Laskey and Costa(2010);Moura and Roisenberg(2015)],Tab.1 gives the corresponding relation between language variable and membership degree suitable for Chinese context.In order to reduce the complexity,the average value was taken and the middle value in the interval was selected.Except the extreme case where 0 and 1 are taken in extremely low and high situations,the membership degree αAj:j≠iof other states ψ(θ)can be obtained using one of the following methods:

1)If Aj:j≠ihas language description only and no membership degree function,αAjcan be obtained through the corresponding relation between language variable and membership degree;

2)If Aj:j≠ihas membership degree function,x can be calculated through inverse function,and the membership degree αAjcan be obtained by substitutingxintoand retaining one digit after the decimal place.

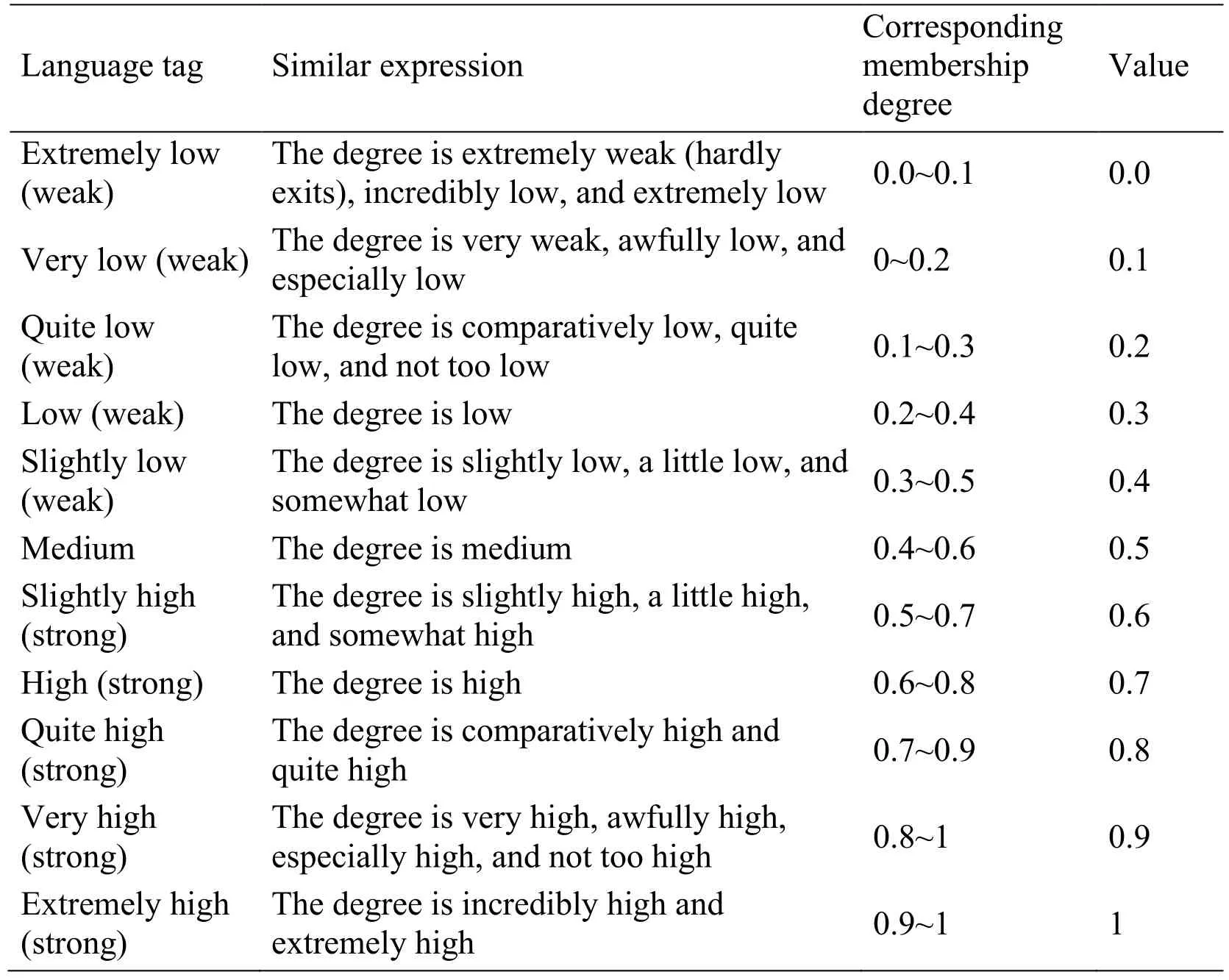
Table 1:Corresponding table of extent description language and fuzzy membership degree

To further explain 2),two examples are given in the following.Suppose the random variable “weather” has two states{sunny,cloudy},and the current description is comparatively cloudy.According to Tab.1,the membership degree should be(0.2,0.8).If the sum of membership degrees of states is not equal to 1,standardization should be done to make the sum equal to 1.By taking “height” as an example,if we just know that someone is “very high”,the fuzzy membership degree of state “high” can be 0.9,and the rough height value x can be calculated through the inverse function.The membership degrees of“short” and “medium” can then be calculated throughμshort(x)andμmedium(x),that is,if αAℎigℎ=0.9,then αAsℎort=0,αmedium=0.1.

3.2.2 Fuzzy IF-THEN rule

In formal knowledge representation of reasoning system,IF-THEN rule is one of the basic approaches to represent the knowledge.This section will further expound the reasoning process of IF-THEN rule with the fuzzification.

The general format of fuzzy IF-THEN rule is “IFxisAi,THENyisBj”,which decides the causal relationship of language variable[Zadeh(1968)].In this rule,xis the input variable,yindicates the output variable,andAiandBjrepresent the natural language values corresponding to the variables.They are represented with the fuzzy set determined by the model input.

In IF-THEN rule of fuzzy MEBN,yandxrepresent the random variableψ(θ)and the language variable of its parent node πo(ψ(θ))respectively.Suppose thatand Boare the natural language values of variables;andrepresent the domain of discourseof rule o and the fuzzy set in Yorespectively.The IF-THEN rule can be simply represented by the following if-then rule statements:

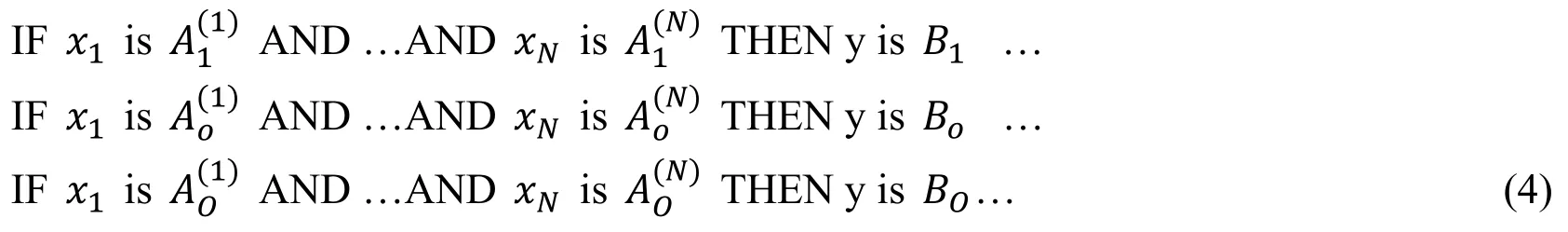
where O is the number of rules;N is the number of input variables;and Boindicate the language values of input random variables x1,…,xNand output random variableyof IF-THEN rule o;the fuzzy sets can be obtained through the method of the previous section,and denoted byrespectively,in whichand βjare the membership degrees of fuzzy states in fuzzy setsandseparately,is the number of states of input variable xι,andis the number of states of output variabley.

Table 2:IF-THEN reasoning

As shown in Tab.2,under the condition thatis given,according to Eq.(2),conclusioncan be calculated by Eq.(5):

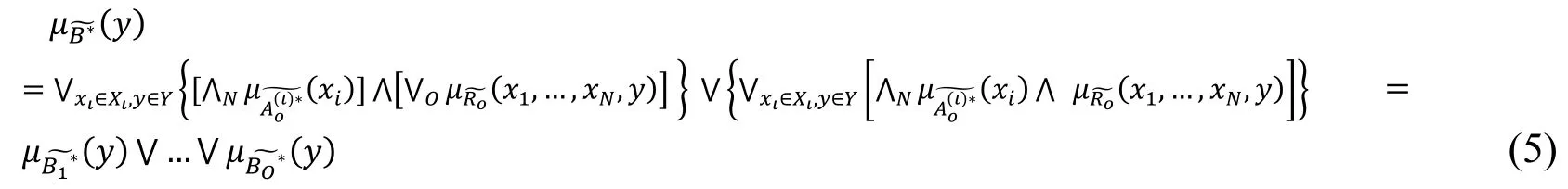
Each fuzzy MEBN node contains fuzzy and probabilistic information at the same time.Besides the IF-THEN rule,the Fuzzy PR-OWL ontology can also show the conditional probability distribution.When the conditional probability distribution is given,the fuzzy probability can be calculated through the following reasoning.The joint probability ofis the probability of fuzzy event,and can be calculated by Eq.(6):

The probability of fuzzy event Aocan be calculated by Eq.(7):

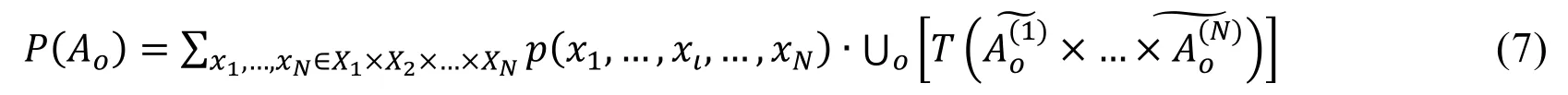
where T is the t-norm operator of weak conjunction calculated by the minimization process,× is the Cartesian product,and ∪isthe maximization operator.

3.2.3 Fuzzy belief propagation algorithm

In the BN reasoning algorithm,if Bayesian Network is small,simple marginal summation can meet the requirement,but the practical problem often involves a large scale.The overall operation complexity and data will show exponential growth.If the Belief Propagation algorithm is used to solve such a network problem,the operation complexity will only have a linear correlation with the number of nodes.Therefore,the Belief Propagation algorithm plays an increasingly important role when dealing with large-scale Bayesian network reasoning problems.

The Clique Tree algorithm,also known as the Junction Tree algorithm,was proposed by Lauritzen et al.[Lauritzen and Spiegelhalter(1988)].The Clique Tree algorithm is the fastest Bayesian reasoning algorithm at present.The algorithm first converts the Bayesian network into a clique tree,and then performs calculation through message passing.The message will be broadcasted to every node of the clique tree to ensure consistency.

In the Clique Tree Belief Propagation algorithm,every clique tree is set as a node to send message to neighbor nodes.Let clique treeTbe composed of clique C1,C2,…,Ck.Each φ∈Φ is assigned to clique α(φ),and the initial potential energy of Cjis defined by Eq.(9):

In the equation,local evidence is corresponding to the prior probability or conditional probability of every node,i.e.,.For instance,P(a)=

For clique Ci,βiis initialized as ψiaccording to Eqs.(9)and(3):

Clique Cimultiplies all other neighbor messages with the initial clique potential energy,adds up all variables except variables in the cut set of Ciand Cj,and sends the result to Ci.Clique Cinode transmits the updated messages to other nodes after receiving messages of its neighbor nodes.The ultimate potential energy of Cican be obtained by Eq.(11):

The messages of Ciand Cjare calculated by Eq.(12):

where(1)bis Boolean number,indicating whether “0” exists in all mki.If “0” exists,b=t(true);otherwise,b=f(false);(2)zis the product of all messages whose value is not zero,i.e.,.

In addition,the zero-perception table can also identify zero,and maps variable example into data that can detect zero.Suppose that Ψ is the table with zero detection and Φ is the standard table without zero detection,real(Ψ)is the standard table containing results obtained viareal(z,b)in table Ψ.

The specific steps of Belief Propagation algorithm based on fuzzy probability are as follows:

(1)Initialization

The fuzzy set of(input or output)variable is obtained through fuzzification according to the language value of variable,and the generated SSFBN is divided.For every clique Ci,is calculated to initializeusing Eq.(10).The parameter of real(z,b)is initialized to(1,f).

(2)Information transfer

The message is transferred from the leaf node to the root node,and then transferred from the root node to the leaf node.In all directions,every cut set Si,jwill consider Φi,jas the previous message transmitted along the edge(i-j).This message can prevent repeated calculation,and every node will immediately update its belief after receiving messages from other nodes.It will multiply its belief with newly received message and divide the result by the message received from the same nodes last time.Hererealfunction is used to avoid meaningless message.

The algorithm of Fuzzy-Probability Belief Propagation(FPBP)

ProcedureJTree-FPBP(Φ,T)//Φ:set of factors,T:clique tree inΦ

ProcedureInitialize-JTree(T)//Initialize the clique method

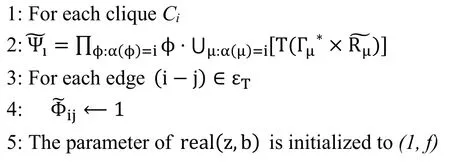
ProcedureMessagePropagation(i,j)//Message passing method:isending clique,j receiving clique

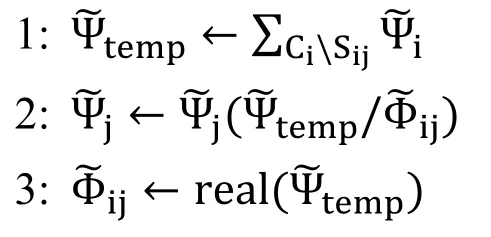
3.3 Establishment and reasoning of Situation-Specific Fuzzy Bayesian Network(SSFBN)

The premise of MEBN reasoning is the generation of Situation-Specific Bayesian Network,i.e.,SSBN.The minimum BN that satisfies the query request is first obtained through MTheories of domain-specific knowledge and a group of observed results,and then the reasoning algorithm of Bayesian network is used to calculate the posterior probability of searching for the set of target random variables gathered from observation evidence.

The algorithm of Fuzzy MEBN is a simple bottom-up algorithm and starts from the finite set containing target random variables and finite set of random variables gathered from observation evidence.The two sets are combined to build an approximate SSFBN.In the approximate SSFBN,if one node is the parent of another node or the context variable of its superior FMFrag,an edge between the two nodes is added.In each step,the algorithm builds a new approximate SSFBN by adding evidence nodes and instantiates superior FMFrags of random variables in the query sets and their ancestor nodes.The result random variables are added to the query set,any node irrelevant to query is removed,and the result sets of random variables are combined to create a new approximate SSFBN.The above process repeats until the approximate SSFBN remains unchanged or the stopping condition is met.If the algorithm has no stopping condition,the result of the algorithm is either an accurate response or a warning that the evidence information is inconsistent when the construction of SSFBN is done.If the algorithm does not stop,it produces many approximate SSFBNs that can generate correct query responses.Generally speaking,there is no evidence of finite length consistent with the query fragment,but inconsistent query fragments can be detected when SSFBN is constructed.

To minimize the final SSFBN and improve the reasoning efficiency,while constructing SSFBN,evidence node,target node and internal node are retained while redundant node,barren node and d-separated node irrelevant to the ultimate result or with a small influence are removed.

Suppose thatEis the set of observed evidences,Qis the set of queries,Bis Bayesian network,andVis the set of nodes.The construction process of SSFBN is consists of the following steps:

(1)Initialization

The set of queriesQis set to be the union set of random variables of target nodes and evidence nodes;the random variable exampleR0 is set to be Qand the set of evidencesE is set to be null;the maximum numberN0of states of every random variable is a positive integer user specified.

(2)SSFBN Construction

Suppose that the current SSFBNBiincludes nodes inRi,and all edges are defined in influential configurations.Remove any isolated nodes fromBi,and conduct dseparation from target nodes to evidence nodes,without updating the marginal distribution of nuisance nodes.Whenever a new evidence is added toE,a new SSFBN is constructed and any unnecessary node,such as barren node BNode(v)or worthless node NNode(v),including d-separated node connected to target node and marginal distribution node,is removed.Later,the FPBP algorithm in Section 3.2.3 can be used to calculate local distribution.Finally,the FBN algorithm is run according to Fuzzy Belief Propagation on the manicured networkBaccording toQandE.The goal of this algorithm is to construct the Bayesian network of context that meets the consistency condition.

In the SSFBN construction algorithm,the situation-specific random variable node is generated based on query variableQand evidence setE.The context node of every random variable has passed satisfiability test.If the condition is met,this node and its parent node will be created.

SSFBN construction algorithm

ProcedureGenerate-SSFBN(Q,E)

FBN reasoning algorithm

ProcedureFBN-Reasoning(B,Q,E)

(3)Local distribution construction

We set local distribution inBi,modify the local distribution and restrict random variables toNipossible values,and estimate the influence of random variables not listed.Besides,the calculation should not exceedKisteps.

(4)Reasoning

Given evidence random variables,we calculate the local distribution of target random variables via the FPBP algorithm in Section 3.2.3.We run the Fuzzy Belief Propagation algorithm on the manicured networkBaccording toQandE,and calculate the conditional probability distribution of non-query nodes.Inconsistency of evidences is reported if the evidence random variable has probability 0,and if the query contents are consistent,the random variable of query set of the current SSFBN,Ri,is outputted.

(5)Example enumeration and approximate parameter updating

If the stopping condition is met,outputRi.Otherwise,the parent nodes of other random variables ofRiis added.As the distribution might be changed when extra parent nodes are added,NiandKiare added before going to Step 2.

4 Experiment and analysis

We used the tenfold cross validation method to evaluate the veracity of the FPBP algorithm by comparing it with the classic Belief Propagation algorithm(BP).Our test dataset is Iris,which consists of 50 samples from each of three species of Iris(Iris virginica,Iris setosa,andIris versicolor)and each sample has 4 attributes:sepal length:4.3 cm～7.9 cm;sepal width:2.0 cm～4.4 cm;petal length:1 cm～6.9 cm;petal width:0.1 cm～2.5 cm.

The goal of our experiment was to predict the specie of an Iris flower from four attribute values including sepal length,sepal width,petal length,and petal width,as shown in Fig.6.

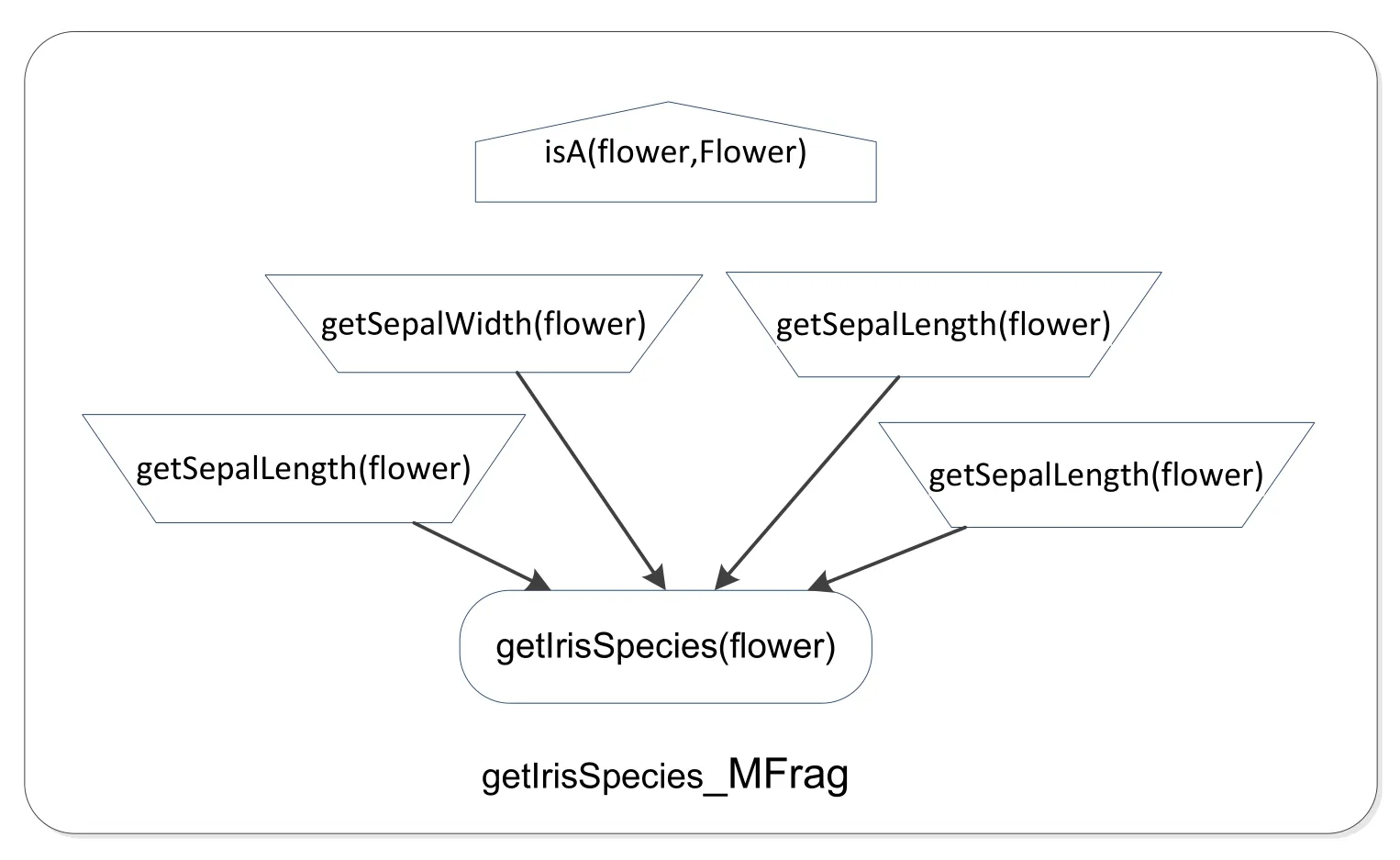
Figure 6:Species fragment of Iris

In the experiment,random variables,such as sepal lengthgetSepalLength(flower),are classified into three categories:short,medium and long.For the training data,the values in the sepal length column are first sorted in ascending order and the resulting sequence is bi,1,bi,2,…bi,nwhere the first subscriptiis the column index number,the second subscript represents the index in the sequence,andnis the size of training set.Then the sequence is equally divided into three parts and the boundaries of three categories can be determined,i.e.,short(＜ b1,n/3),medium(b1,n/3,b1,2n/3)and long(＞ b1,2n/3).Similar method can also be used to classify other random variables,as shown in Tab.3.

Table 3:Category table of random variables of Iris

By aiming at the characteristics of Iris dataset,the triangle membership degree function was used to calculate the membership degree from the values of random variables like petal length.Fig.7 shows the membership degree function of the Iris dataset,in whichais equivalent to the minimum value of random variable,bis the median bi,n/2of the attribute sequence,andcis the maximum value of this attribute.For instance,a,the membership degree of petal length random variable,has the minimum value(1 cm),bis the median(b3,n/2)of the petal length sequence b3,1,…,b3,n/2,…,b3,n,andcis the maximum value(6.9 cm).Suppose that the petal length of a specific line of data in training set isx.The membership degree vector can be calculated by using the membership degree function.

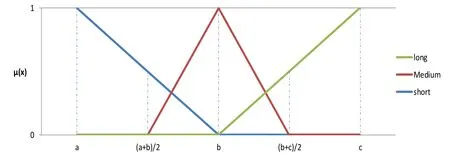
Figure 7:Membership degree function of Iris

We chose the tenfold cross validation method,which is the veracity test method of the common algorithm,to evaluate our proposed solution.We first create 10 sample data sets from the Iris dataset.9 of them were set as the training data in turn and 1 was used as the test data.The average classification accuracy(or error rate)of 10 runs was used to measure the performance of the algorithm.

Tab.4 shows the tenfold cross validation results of the proposed FPBP algorithm(retain two digits after the decimal point).Meanwhile,we applied the same validation process to the BP algorithm using the same 10 sample data sets and compared the performance of two algorithms.As shown in Tab.5,the average classification accuracy of FPBP is 89.2%,which is nearly 34% higher than the average accuracy of BP(66.7%).Obviously,FPBP,the fuzzy probability algorithm that adds fuzzy membership degree calculation,has higher accuracy than the BP algorithm that simply calculates the probability,which demonstrates the veracity and validity of our algorithm.

Table 4:Experimental results of tenfold cross validation of FPBP

Table 5:Comparison of average classification accuracy between FPBP and BP

The time complexity of the BP algorithm on the Iris dataset is T(n,s,p)=T1(n)*T3(p)*T2(s)=O f(n)* φ(p)*g(s),in whichnis the size of dataset,prepresents the number of random variables like petal length,andsis the number of variable states.By adding matrix multiplication related to number of categories,the time complexity of FPBP is as following:

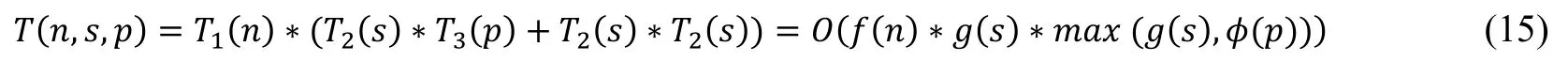
In practice,the size of data is often greater than the number of attributes and the number of categories,and the number of attributes is greater than the number of categories.Therefore,compared with the BP algorithm,the increase in time complexity of the FPBP algorithm is still within a reasonable range.

5 Conclusions and future work

In this paper,by integrating the Belief Propagation algorithm of Bayesian network with the fuzzy probability theory,a fuzzy belief propagation algorithm is proposed and applied to the representation and reasoning framework of Fuzzy PR-OWL ontology.Besides,the framework from ontology analysis to reasoning model was created for representation and reasoning of fuzzy probability knowledge.According to the tenfold cross validation experiment results and the time complexity analysis,the FPBP algorithm has much higher classification accuracy than the BP algorithm without increasing the time complexity too much.

Although this paper has made some progress in reasoning study about fuzzy probability ontology,due to increasing complication and expansion of ontology,researchers in the field of uncertainty reasoning of ontology are still faced with many challenges.For example,the veracity of our algorithms highly depends on the selection of the membership degree function,and how to select appropriate membership degree function can be further explored.In addition,although our algorithm can handle most fuzzy probability reasoning problems of various scales,the efficiency can be further improved when the node number reaches a certain scale.

Acknowledgments:The authors are grateful to the editors and reviewers for their suggestions and comments.This work was supported by National Key Research and Development Project(2018YFC0824400),National Social Science Foundation project(17BXW065),Science and Technology Research project of Henan(1521023110285),Higher Education Teaching Reform Research and Practice Projects of Henan(32180189).