基于分数阶微积分PDλ比例导引的无人机自动避撞方法

贾耀强,孙雪

基于分数阶微积分PD比例导引的无人机自动避撞方法

贾耀强,孙雪*

东北林业大学 机电工程学院, 黑龙江 哈尔滨 150040

为了进一步改善无人机自动避撞方法，本文首先给出了基于碰撞锥检测方法，然后设计了分数阶微积分PDλ比例导引方法，最后采用简单迭代法实现了避撞时间在线估计。仿真结果表明：该方法参数较少，计算简单。相比较传统比例导引方法而言，该方法过载需求小和较快的收敛速度，且能够较好地抑制风扰动，具有较强抗干扰性。

无人机;自动避撞

随着无人机在世界范围内的广泛应用，无人机的感知与避撞已成为至关重要的问题。目前，无人机尚缺乏必要的感知与避撞能力，因此，无法实现与有人机共享同一片空域。

在无人机避撞方面，主要包括导引方法[1]和路径规划方法。由于导引方法计算简单，实施性强，研究的主要思路是首先通过碰撞检测方法检测可能发生的碰撞，然后采取合适的避撞方法，在一定的性能指标和约束下进行避撞飞行。

近年来国内外学者对导引方法进行了大量的研究。在无人机非协同避撞领域，将导弹拦截控制中的导引方法[2]应用于无人机避撞飞行控制是一类有效的方法，主要有基于比例导引、微分几何导引、非线性动态逆导引、智能导引的避撞方法等。传统的比例导引方法只针对静态障碍或者非机动障碍，当存在较大的扰动时，无人机避撞的安全性能得不到保证。文献[3]采用最优比例导引律实现无人机三维避撞并推导出了最优比例导引系数的计算方法。虽然简化了导引指令的计算，但这类以视线角为基础的导引指令仍然是非线性的。每一时刻的导引指令需要计算当前无人机飞行状态信息，造成避撞时间的估计模型没有解析解。

避撞时间是无人机避撞过程中一个非常重要的参数。当采用不同的导引指令时，相对速度跟踪到碰撞锥边界的时间不同，导致避撞机追踪避撞点的时间也不同。因此需要对避撞时间进行估计。通过对避撞时间的限制，可以估计避撞机需要机动的范围。多种改进的比例导引方法均依赖于精确的避撞时间估计。

无人机避撞时间与导弹拦截控制中的拦截时间有相似的地方。在导弹拦截领域，Ghose提出一种精确求解传统比例导引下的导弹拦截时间[4]。利用存储的基本解以及多项式系数通过数值插值的方法计算不同比例导引系数下的拦截时间。2016年他又提出了一种统一的适用于传统比例导引和负比例导引的时间估计方法，这种估计方法将时间估计分为两部分，第一部分计算视线角收敛到零的时间，第二部分是拦截器拦截目标的时间。

相比较传统的比例导引方法[5]和PID导引方法，分数阶微积分导引方法控制更加灵活，具有更强的抗干扰性。文献[6]提出一种分数阶修正比例导引方法用来解决导弹拦截点过载突变的问题。文献[7]提出一种基于分数阶微积分PDλ比例导引制导律，具有拦截精度高、参数不敏感、鲁棒性强等优点。但是以上分数阶微积分导引方法均在导弹拦截领域应用，并不能直接用于无人机避撞领域。目前在无人机避撞领域相关文献较少。因此，本文提出一种基于分数阶比例微分导引的无人机自动避撞方法，用来提高避撞系统的灵活性以及鲁棒性能，来保证避撞的安全。

1 碰撞检测方法

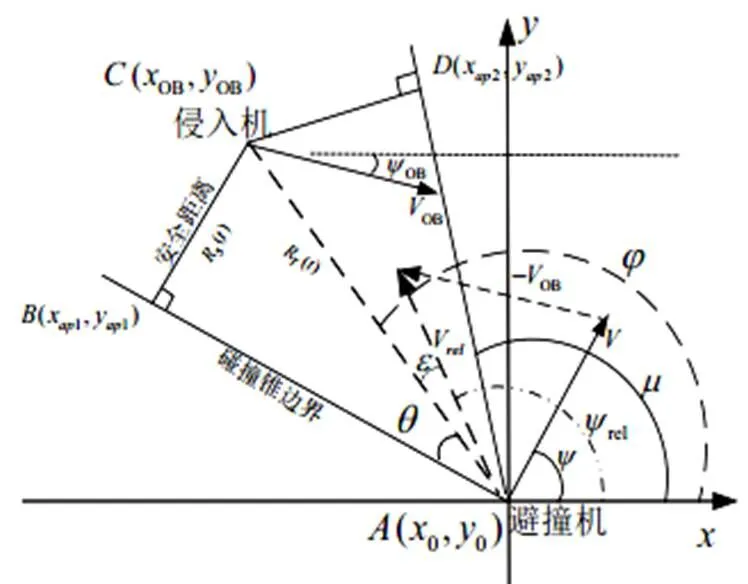
图1 碰撞锥相对几何关系图

|-Ψ|<(1)

式中，为视线角(LOS)，为避撞机与侵入机相对航向角。为碰撞锥的半顶角。因此，只要式(1)满足，在未来飞行的某一时刻，两无人机的间距将小于给定的安全距离，避撞机与侵入机可能发生碰撞，则无人机需执行避撞策略进行避撞飞行。

根据避撞机与侵入机相对运动以及式(1)可得到无人机避撞成功的条件为，在避撞机到达避撞点B点或者D点之前，式(2)成立。

|-Ψ|≥(2)

避撞机避撞成功意味着在避撞机到达避撞点之前，避撞机与侵入机的相对速度向量V至少要跟踪并收敛到碰撞锥边界。如果V落在碰撞锥外，避撞一定是成功的。

2 分数阶PDλ导引律设计

2.1 避撞系统总体设计

当检测到避撞机与侵入机可能发生碰撞之后，避撞机执行合适的避撞策略进行避撞。本文主要采用基于分数阶PDλ导引律的自动避撞方法。自动避撞系统控制框图如图2所示。

图2 自动避撞系统控制框图

图2中，利用机载传感器可以获得避撞机与侵入机的飞行状态信息，例如无人机位置、速度以及航向角等。以这些飞行状态信息为输入，经过导引控制环可得到导引指令，作为姿态控制环的给定值，以无人机横侧向为例，无人机得到导引指令继而得到给定滚转角，通过调整无人机航向角实现协调转弯。

2.2 分数阶PDλ导引律设计

首先给出分数阶微积分基本操作算子的表达式：

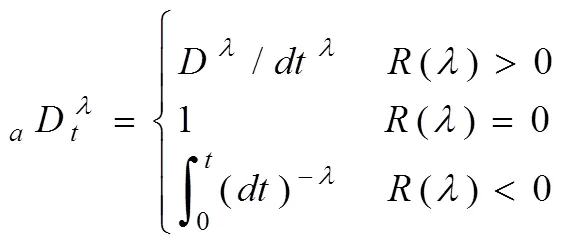
式中，，是微积分的上下限，为微积分的阶次。

因此，我们定义误差如下：

=-(5)

其中：

式中，R为两无人机间距。采用分数阶比例微分控制，可以得到微分方程如下：

式中，k和k为分数阶比例微分导引系数。e为误差e的分数阶次微分。将式(5)代入式(7)中可得：

根据图1的几何关系可得：

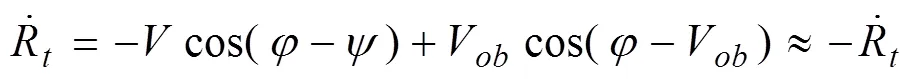
式中，和V分别为避撞机与侵入机的速度，和Ψ分别为避撞机与侵入机的航向角。

式(9)对时间求导可得：

整理式(11)可得：

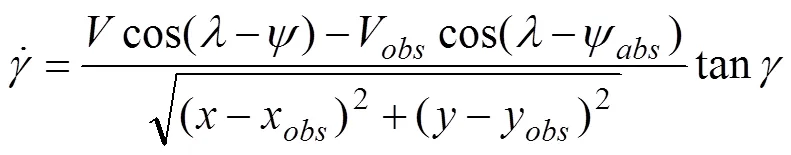
分数阶PDλ导引律设计如下：

分数阶PDλ导引律中包含3个设计参数，比例导引系数k、微分导引系数k、分数阶微分阶次。

相比较传统的比例导引方法和PD型的导引方法，具有较灵活的控制，参数选择范围更广，参数适应性更强，具有较强的鲁棒性。目前，对于分数阶PID控制器参数整定的方法，基于遗传算法和粒子群算法的参数整定和优化方法已经比较成熟[8]，在这里不多加叙述。

3 避撞时间估计

避撞时间是无人机避撞过程中非常关键的参数。精确的避撞时间估计可以提高无人机避撞精确度，减小无人机机动范围。当自抗扰导引方法的参数确定后，避撞时间可以通过以下方法进行估计。

控制量简化为：

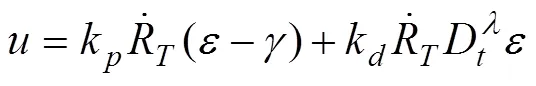
避撞时间分为两部分：一部分是相对速度跟踪碰撞锥边界时间1，一部分是无人机跟踪避撞点时间2。无人机通过改变横侧向滚转角改变无人机航向，因此无人机横侧向动态模型可简化为：

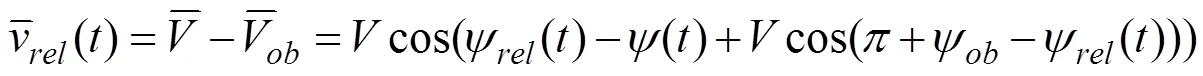
当无人机相对速度跟踪到碰撞锥边界时，可得到：

将式(15-19)代入方程式(20)中，通过简单迭代方法即可求解避撞时1。第二部分无人机避撞的路径为保持1时刻航向角匀速飞行的直线。避撞点的坐标可通过式(21)求解。

第二部分的避撞时间2可通过式(22)求解：

4 仿真验证

4.1 仿真验证初始条件

为了验证提出的分数阶PDλ导引方法的性能，本文采用Matlab搭建六自由度无人机仿真实验平台。以横侧向无人机自动避撞为例，当式(1)成立时，无人机开始避撞，避撞机高度和速度保持恒定，避撞机通过协调转弯来改变避撞机航向角实现避撞。

避撞机副翼和方向舵动态特性如下：

式中，δ和δ分别为副翼和方向舵偏角。μ和μ分别为副翼和方向舵的输入。

设定安全距离为R=2 km避撞机与侵入机的初始高度为6 km。避撞机与侵入机仿真初始条件如表1和2所示。

表1 避撞的初始条件

表2 侵入机的初始条件

根据第三部分的避撞时间估计方法可得到两个案例的避撞估计时间如表3所示。

表3 避撞完成时间估计

4.2 仿真案例

4.2.1 案例一此案例中，避撞机的速度与侵入机的速度相同。避撞机与侵入机初始航向夹角为5/6。通过和传统的比例导引避撞方法比较，来验证分数阶PDλ导引方法的性能。导引系数为k=3.3，k=1，=-1.1。避撞轨迹如图3所示。

图3 案例一避撞机与侵入机的避撞轨迹

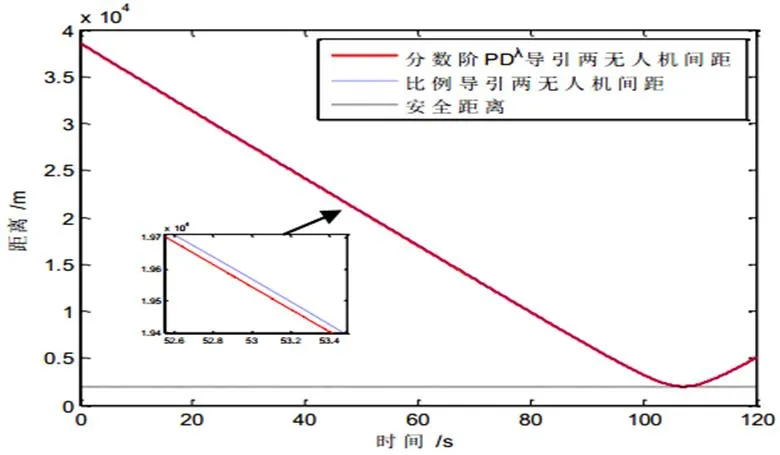
图4 案例一避撞机与侵入机间距

图3中，在第七个采样圆时刻附近，两采样圆相切。避撞机与侵入机的间距到达最小。两种导引方法均能避撞成功。采用基于分数阶PDλ导引方法的避撞机机动范围要小于传统比例导引方法的机动范围。

从图4中可以看出，在107 s时，避撞机与侵入机间距达到最小值，等于给定的安全距离。避撞成功。整个避撞过程中，采用基于分数阶PDλ导引方法的避撞机与侵入机间距始终小于传统比例导引方法。

图5中，分数阶PDλ导引方法的避撞机滚转角以及导引指令要小于传统比例导引方法，过载需求小。而且两种方法的收敛速度相近。在107 s时避撞完成，与表3中估计的避撞时间104 s误差为3 s。

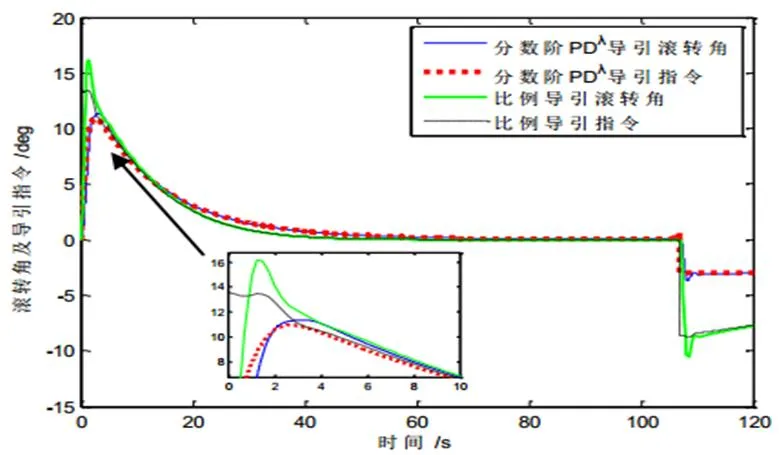
图5 案例一避撞机滚转角及导引指令

图6 案例一避撞机副翼及方向舵偏角

图6中，两种方法中的方向舵偏均较小。基于分数阶PDλ导引方法的副翼舵偏要明显小于传统比例导引方法。两种导引方法的舵面偏转均小于舵偏的限幅值20°。

4.2.2 案例二案例二中，避撞机的速度要小于侵入机的速度。避撞机与侵入机初始航向夹角为π/2。在仿真时间30 s加入幅值为20 m/s的常值风扰动。避撞轨迹如图7所示。

图7中，在第8个采样圆时刻附近，避撞机与侵入机采样圆相切，避撞机与侵入机间距达到最小值。尽管存在风扰动，但同一时刻避撞机与侵入机采样圆并未相交。避撞机避撞成功。

图7 案例二避撞机与侵入机的避撞轨迹

图8 案例二避撞机与侵入机间距

图8中，在存在风扰动的情况下，避撞机与侵入机间距始终大于或等于给定的安全距离，避撞机避撞成功。避撞时间为110 s，与表3中估计的避撞时间110 s误差为2 s。

图9 案例二避撞机滚转角及导引指令

图10 案例二避撞机副翼及方向舵偏角

图9中，由于在30 s时加入常值风扰动，根据分数阶PDλ导引方法计算出新的导引指令来抑制风扰动。滚转角峰值小于14°满足无人机横向过载要求。

图10中，副翼舵偏峰值小于9°，明显小于舵面偏转的限幅值20°。在仿真时间30 s时，由于存在风扰动，产生副翼舵面偏转来抑制风扰动。

5 结论

本文提出一种基于分数阶PDλ导引的无人机自动避撞方法并完成了仿真验证，得到了以下结论。

（1）该无人机自动避撞方法所产生的导引指令计算简单，在多种避撞初始条件下均能避撞成功。利用简单迭代法实现了避撞时间的在线估计。

（2）相比较于传统比例导引方法，分数阶PDλ导引具有过载要求小的优势，而且收敛速度相近。通过仿真分析可知该避撞方法具有较强的抗扰性能。能够很好的应对风力干扰等扰动。

[1] Yu X, Zhang Y. Sense and avoid technologies with applications to unmanned aircraft systems: review and prospects[J]. Progress in Aerospace Sciences, 2015,74:152-166

[2] 吕永佳,张合新,李正文,等.自抗扰三维最优比例滑模导引律设计[J].科学技术与工程,2011,11(12):2814-2818

[3] Han SC, Bang H, Yoo CS. Proportional navigation-based collision avoidance for UAVs[J]. International Journal of Control, Automation and Systems, 2009,7(4):553-565

[4] Dhananjay N, Ghose D. Accurate time-to-go estimation for proportional navigation guidance[J]. Journal of Guidance, Control, and Dynamics, 2014,37(4):1378-1383

[5] 叶继坤,韦道知,李炯,等.基于分数阶微积分理论的新型三维末制导律[J].固体火箭技术,2016(3):428-435

[6] 朱竹婷,廖增,彭程,等.一种分数阶修正比例导引律[J].控制理论与应用,2012,29(7):945-948

[7] 王飞,雷虎民.基于分数阶微积分PDλ比例导引制导规律[J].控制理论与应用,2010,27(1):126-130

[8] 闫玺.分数阶PID控制器及其参数整定的研究[D].西安:西安理工大学,2014

A Method Auto-avoiding UAV Collision Based on Fractional Calculus PDλGuidance

JIA Yao-qiang, SUN Xue*

150040,

To further improve a method auto-avoiding UAV collision, firstly the detection method based on the collision cone was proposed, and then the fractional calculus PDλguidance method was designed, at last collision time estimation on line got by a simple iterative method. The simulation result showed the method had fewer parameters and a simple calculation. Compared with the traditional proportional guidance method, it required a small overload and faster convergence speed, and was able to control a wind disturbance and had a stronger anti-interference.

Unmanned aerial vehicle, UAV;automatic collision avoidance

V279+.2

A

1000-2324(2019)05-0855-06

10.3969/j.issn.1000-2324.2019.05.026

2018-03-25

2018-05-09

贾耀强(1997-),男,本科生,研究方向智能控制与智能系统. E-mail:jiayaoqiangzq@foxmail.com

Author for correspondence. E-mail:xuesun@hit.edu.cn