一种公开参数长度固定的非零内积加密方案*
2019-11-07高海英
魏 铎, 高海英, 赵 建
解放军战略支援部队信息工程大学, 郑州450001
1 引言
函数加密[1,2]是一种先进的密码学模型, 有望极大地提高加密数据的可用性.内积加密是一类特殊的函数加密, 与传统公钥密码相比, 内积加密能够实现对密文的细粒度访问控制, 在云计算等新兴领域有着广泛的应用.内积加密分为零内积加密和非零内积加密两类.本文研究的是非零内积加密方案, 即在内积加密方案中, 密文和密钥分别与向量x,y相关, 只有x与y满足xTy=1 时, 才可正确解密.内积加密可以看作是基于身份加密的一般化, 它可以作为一种工具来构造谓词加密、属性基加密和公钥可搜索加密等密码方案.
近年来, 一系列内积加密方案相继被提出.2008 年Katz[3]等人提出谓词加密体制概念, 并构造出首个基于整数的内积加密方案, 比较完美的展现了内积加密的本质.2010 年, Lewko[4]等人利用双对偶向量空间(dual pairing vector space)[5,6]技术, 设计了第一个适应安全的内积加密方案, 虽然方案安全强度比较高, 但方案的公开参数选取与属性个数呈线性相关.同年, Okamoto[7]等人借鉴文献 [3]的思想, 提出一个可分层的内积加密方案, 并且方案实现了适应安全, 但方案公开参数规模较大, 导致方案实用性不强.2012 年, Okamoto[8]等人利用Waters[9]提出的双系统加密(dual system encryption) 技术提出了一个适应安全的内积加密方案, 虽然该方案较方案 [7]实现了更强的属性隐藏, 但方案的公开参数规模随着属性个数的增加而迅速扩大, 导致参数规模过大, 方案实现效率比较低.由已有方案可以看出, 设计一个公开参数长度固定且具有适应安全性的内积加密方案是一个有待解决的问题.
本文基于Chen 等人[10]提出的素数阶双线性熵扩张性质, 提出了一个公开参数长度固定的非零内积加密方案, 方案是基于素数阶群双线性映射设计的, 在方案的密钥生成算法中, 将每个属性与随机向量结合, 为每个属性生成私钥分量; 在加密算法中, 利用随机向量与矩阵结合的方法生成密文.基于素数阶双线性熵扩张引理和MDDHnk,k+1困难假设证明了该方案具有适应安全性, 并且公开参数规模明显较少.
2 预备知识
2.1 符号说明
A,a: 矩阵A, 向量a
span(A): 矩阵A列向量张成的线性空间
spank+1(A): 矩阵A列向量张成的线性空间中的k+1 个向量模p剩余类环上m×n维矩阵集合、m维向量集合
(A1|A2|A3):Zp上3 个矩阵的连接

2.2 双线性映射
定义 1(非对称双线性映射)[11]设G1、G2和GT为三个阶为素数p的乘法循环群, 且g1,g2分别是G1,G2的生成元.对于映射e:(G1,G2)→GT称其为非对称双线性映射, 如果其满足以下三条性质:
(1) 双线性性: 对于 ∀a,b∈Zp, 有
(2) 非退化性:e(g1,g2)1,g1,g2均不是单位元.
(3) 可计算性: ∀g∈G1,h∈G2, 均可在多项式时间内计算出e(g,h).
假设群生成算法ς的输入安全参数为 (1λ), 输出元组为 (p,G1,G2,GT,g1,g2,e), 其中p为素数,g1,g2分别为G1,G2的生成元.对于[a]1表示 (g1a1,··· ,g1an), [a]2表示(g2a1,··· ,g2an), [a]T表示e(g1,g2)a, 即 [a]T=(e(g1,g2)a1,··· ,e(g1,g2)an).e:G1×G2→GT是一个非对称双线性映射, 将映射e扩展到向量与矩阵上运算形式如下:
2.3 困难假设
2.4 非零内积加密方案形式化定义
一个非零内积加密方案由以下四个多项式时间算法构成:
Setup(1λ,1n): 该概率初始化算法输入安全参数(1λ,1n), 输出系统公开参数mpk 和主密钥msk.
Enc(mpk,x,m): 该概率加密算法输入公开参数mpk, 向量和明文m, 输出密文ctx.
KeyGen(mpk,msk,y): 该概率密钥生成算法输入主密钥msk 和向量输出密钥sky.
Dec(mpk,sky,ctx): 该确定性解密算法输入 sky和 ctx, 若P(x,y)=1(即xTy=1), 则可解密密文.
2.5 非零内积加密方案的适应性安全模型
下面通过挑战者B和攻击者A之间的交互游戏给出非零内积加密方案的适应性安全模型.
Setup: 挑战者B运行方案的初始化算法,将生成的公开参数mpk 发送给攻击者A,保留主密钥msk.
Phase 1: 攻击者A自行选择y′进行任意多项式次密钥查询.挑战者B运行 KeyGen 算法, 将生成的密钥发送给A.
Challenge: 攻击者A向挑战者提交两个等长的明文m0和m1, 以及要挑战的向量x∗, (任何询问y′与要挑战x∗都不满足 (x∗)Ty′= 1), 挑战者B随机选取b∈ {0,1}, 计算 ctx∗ = Enc(mpk,x∗,mb), 并将ctx∗作为挑战密文返回给攻击者A.
Phase 2: 与 Phase 1 相同.
Guess: 攻击者A给出关于b的猜测b′.
如果b′=b, 称攻击者A赢得了此游戏, 定义A在此游戏中的优势为
定义4如果对所有多项式时间的攻击者, 赢得上述游戏的优势都是可忽略的, 则称该非零内积加密方案是适应性安全的.
3 方案描述
本文在Chen[10]等人提出的素数阶熵扩张引理基础上, 提出一个公开参数长度固定的非零内积加密方案, 下面详细介绍方案.
Setup(1λ,1n): 系统初始化阶段输入安全参数λ和系统属性个数n.选取


方案的解密正确性得证.
4 安全性证明
该非零内积加密方案在基于素数阶熵扩张引理和 MDDHnk,k+1困难假设下被证明是适应安全的.在方案的证明过程中“·” 表示向量按分维乘, 下面先介绍安全性证明中涉及的相关概念.
密文分布:


密钥分布:
标准密钥: 由密钥生成算法KeyGen 生成.
熵扩张密钥:
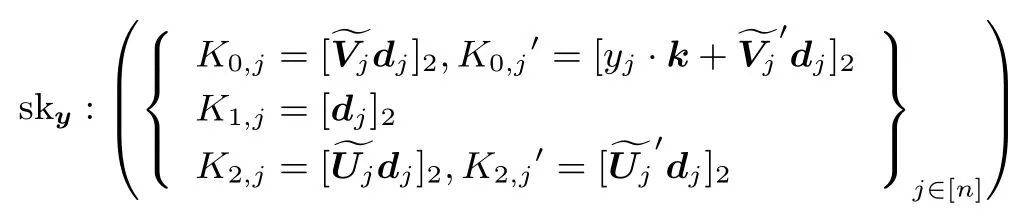
其中dj←span(B).
伪半功能密钥:

半功能密钥: 与伪半功能密钥形式相同, 区别在于dj←span(B).
方案的安全性证明是基于一系列Game 之间不可区分, 假设攻击者A在一次Game 中最多可进行Q次密钥查询, 用Advxx(λ) 表示攻击者A在Gamexx的优势.基于描述的密文、密钥分布, 下面我们详细描述Game 序列, 并在表1 给出了 Game 序列的对比.
Game0: 查询得到标准密钥, 挑战密文是标准密文.
Game0′: 查询得到熵扩张密钥, 挑战密文是熵扩张密文.
Gamei: 查询前i−1 次是半功能密钥、最后Q−i+1 次是熵扩张密钥, 挑战密文是熵扩张密文.
Gamei,1: 查询前i−1 次是半功能密钥、最后Q−i次是熵扩张密钥、第i次是伪标准密钥, 挑战密文是熵扩张密文.
Gamei,2: 查询前i−1 次是半功能密钥、最后Q−i次是熵扩张密钥、第i次是伪半功能密钥, 挑战密文是熵扩张密文.
Gamei,3: 查询前i−1 次是半功能密钥、最后Q−i次是熵扩张密钥、第i次是半功能密钥, 挑战密文是熵扩张密文.
GameFinal: 查询得到半功能密钥, 挑战密文是对随机数加密的熵扩张密文.

表1 Game 序列Table 1 Game sequence
引理 1如果存在一个攻击者A在 Game0和 Game0′的攻击优势满足 |Adv0(λ)−Adv0′(λ)|>ε, 那么可构造一个算法B0以不可忽略的优势区分素数阶熵扩张引理中的左右分布, 且Time(B0)≈Time(A).
证明:挑战者B0得到分布:
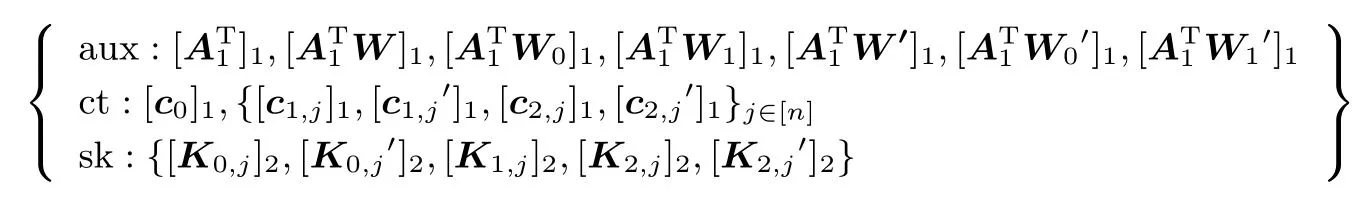
B0需区分该分布是熵扩张引理的左分布, 还是右分布.

Phase 1: 攻击者A申请向量对应的私钥, 挑战者B0模拟密钥生成算法, 在随机选取向量生成向量y′对应的密钥

Challenge: 攻击者A选择两个等长的消息m0和m1, 以及要挑战的向量Phase 1中的向量y′与要挑战x∗向量都不满足 (x∗)Ty′=1) 发送给挑战者B0, 挑战者B0随机选取b∈{0,1},利用向量k以及得到的分布生成挑战密文

Phase 2: 与 Phase 1 相同.
Guess: 攻击者A给出b的猜测b′.
如果挑战者B0得到的是左分布, 那么A询问到标准密钥与得到标准挑战密文, 如果挑战者B0得到的是右分布, 那么A询问到熵扩张密钥与得到熵扩张挑战密文.
如果攻击者A的攻击优势满足 |Adv0(λ)−Adv0′(λ)|>ε, 那么挑战者B0同样以不可忽略的优势区分素数阶熵扩张引理的左右分布.
引理 2由表1, 可以得到 Game0′≡Game1.
引理 3如果存在一个攻击者A在 Gamei和 Gamei,1的优势满足 |Advi(λ)−Advi,1(λ)|>ε, 那么可以构造一个算法B1以不可忽略的优势解决问题, 并且Time(B1)≈Time(A).

Phase 1,2: 设将攻击者A对挑战者B1进行第κ次密钥询问, 对应的向量是我们分三种情况讨论:
Case 1:κ 发送给攻击者A. Case 2:κ>i, 挑战者B1利用得到的分布随机选取 [dj]2←span([B]2), 并且利用向量k和攻击者A询问的向量生成熵扩张密钥sky′ 发送给攻击者A. Case 3:κ=i, 挑战者B1针对攻击者A询问的向量并且利用向量k、{[tj]2}j∈[n]和攻击者A询问的向量生成密钥 sky′ 发送给攻击者A. Challenge: 攻击者A选择两个等长的消息m0和m1, 以及要挑战的向量(Phase 1 中的向量y′与要挑战x∗向量都不满足(x∗)Ty′=1)发送给挑战者B1, 挑战者B1随机选取b∈{0,1},随机选取生成挑战密文 Guess: 攻击者A给出b的猜测b. 如果 [t1,··· ,tn]=BS, 那么第i次询问的密钥是熵扩张密钥, 上述游戏对应的是 Gamei, 如果[t1,··· ,tn]=Z, 那么第i次询问的密钥是伪标准密钥, 对应的是 Gamei,1. 如果攻击者A使 |Advi(λ)−Advi,1(λ)| >ε不可忽视, 那么挑战者B1同样以不可忽略的优势区分[t1,··· ,tn]=BS和 [t1,··· ,tn]=Z. 引理 4对于任意攻击者A, 在 Gamei,1和 Gamei,2的优势满足 |Advi,1(λ)−Advi,2(λ)|=0. 证明:Gamei,1和 Gamei,2不同之处仅在于第i次密钥询问, 挑战者在 Gamei,1中用向量k生成伪标准密钥, 在Gamei,2中用生成伪半功能密钥.下面说明这两个游戏无法区分. Setup: 同引理 3 中的 Setup, 在这里挑战者随机选取输出公开参数 Phase 1,2: Gamei,1中挑战者B针对攻击者A的第i次密钥询问的向量随机选取向量生成y′密钥 在 Gamei,2中, 挑战者随机选取生成密钥 可以观察到两个游戏的第i次私钥查询差别仅在于这一分量, 分析这两个分量 由于随机值α以及随机向量的参与,同分布, 故从攻击者角度来看这两种密钥无法区分. Challenge: 由于这两个游戏输出的都是熵扩张挑战密文, 同分布. 由上分析得到 |Advi,1(λ)−Advi,2(λ)|=0. 引理 5如果存在一个攻击者A在 Gamei,2和 Gamei,3的优势满足 |Advi,2(λ)−Advi,3(λ)|>ε, 那么可以构造一个算法B2以不可忽略的优势解决问题, 并且Time(B2)≈Time(A). 证明:与引理 3 证明相似, 只是在密钥查询的时候: 第i次查询用的向量k换成向量针对攻击者A询问的向量挑战者B2利用向量和{[tj]2}j∈[n]生成密钥发送给攻击者A. 如果 [t1,··· ,tn]=Z, 那么第i次询问的密钥是伪半功能密钥, 上述游戏对应的是 Gamei,2, 如果[t1,··· ,tn]=BS, 那么第i次询问的密钥是半功能密钥, 对应的是 Gamei,3.所以如果攻击者A使|Advi,2(λ) − Advi,3(λ)| >ε不可忽视, 那么挑战者同样以不可忽略的优势区分 [t1,··· ,tn]=BS和[t1,··· ,tn]=Z. 引理 6由表1, 可以得到 Gamei≡Gamei−1,3. 引理7对于任意一个攻击者A,在GameQ+1和GameFinal的优势满足|AdvQ+1(λ)−AdvFinal(λ)|=0. 证明:这两个游戏的差别在于 GameQ+1挑战密文是消息mb的熵扩张密文, GameFinal挑战密文是随机数的熵扩张密文.下面来说明这两个游戏不可区分. Phase: 挑战者B3针对攻击者A申请访问的向量随机选取dj←span(B),生成半功能密钥: Challenge: 攻击者A选择两个等长的消息m0和m1,以及要挑战的向量x∗=(x∗1,··· ,x∗n)(Phase 1中的向量y′与要挑战x∗向量都不满足 (x∗)Ty′=1) 发送给挑战者B3, 挑战者B3随机选取b∈{0,1},随机选取向量c,cj,cj′←span(A1,a2), 生成挑战密文 Phase 2: 与 Phase 1 相同. Guess: 攻击者A给出b的猜测b. 由以上分析得到 |AdvQ+1(λ)−AdvFinal(λ)|=0. 定理 1在素数阶熵扩张引理和困难假设成立的条件下, 本文提出的非零内积加密方案是适应性安全的, 并且max{Time(B0),Time(B1),Time(B2)}≈Time(A). 证明:在适应性安全模型下, 攻击者A对本文给出的非零内积方案的攻击优势就是对Game0的攻击优势, 由安全性证明中给出的Game 序列之间的关系, 可得: 由引理 1 知 |Adv0(λ)− Adv0′(λ)|<ε.由引理 2 知 |Adv0′(λ)− Adv1(λ)|=0. Gamei到 Gamei+1的逼近可理解为: 由引理 3–6 知: 由引理 7 知 |AdvQ+1(λ)− AdvFinal(λ)|=0, 攻击者A在 GameFinal中的优势 AdvFinal(λ)=0.综上分析, 得到攻击者A在 Game0中的优势 Adv0(λ)≤ (2Q+1)ε. 本文基于素数阶群上的双线性映射, 设计了一个公开参数长度固定且适应安全的非零内积加密方案,本文与文献 [4,7,8]相比, 虽然在密钥长度与密文长度有所增加, 但是在公开参数长度方面具有绝对的优势, 并且随着属性个数的增加, 文献 [4,7,8]公开参数长度增长程度远大于本文方案.下面给出当k= 1时, 本方案与现有内积加密方案的数据长度对比, 见表2.其中n表示系统属性的个数, |G1|,|G2|,|GT| 分别表示G1,G2,GT中群元素的长度. 表2 与现有内积加密方案的数据长度比较Table 2 Parameter scale comparison with existing inner product encryption schemes 本文借鉴 Chen[10]等人提出的素数阶熵扩张引理, 基于素数阶群双线性映射, 提出了一个公开参数长度固定的非零内积加密方案, 并在素数阶熵扩张引理和困难假设的基础上证明了该方案是适应安全的.与现有内积方案相比, 本文方案的系统公开参数规模大大缩小, 方案操作性和实用性较强.



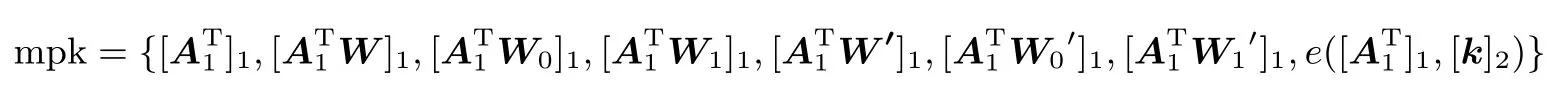
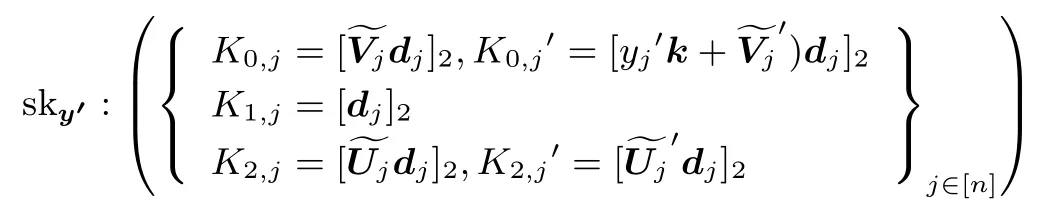


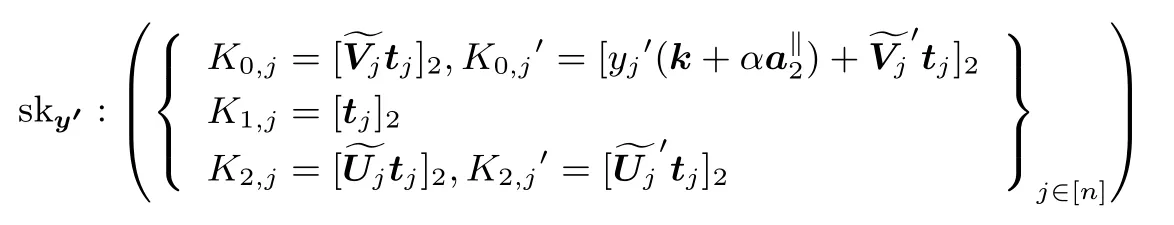


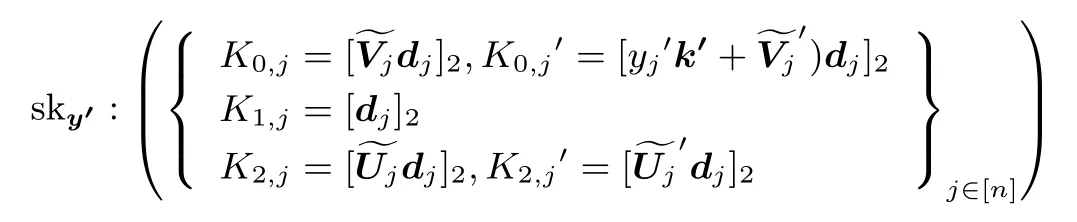





5 性能对比

6 结束语
