基于应变模态的轨道车辆车体应力计算方法
2019-11-06曹辉梁宁赵锦南
曹辉 梁宁 赵锦南


摘要:在轨道车辆结构设计中,分析结构在动载作用下的应力状态是进行强度设计和疲劳寿命估计的关键,但应力不能直接进行测量,一般通过位移模态分析方法建立车体结构位移响应模型,再通过位移与应变的相互关系得到车体的应变响应,进而得到应力状态。由于从位移到应变是微分过程,位移的变动将会得到放大.从而带来误差。利用位移模态理论推导出应变模态理论及其性质.通过车体有限元模型的位移模态及应变模态的仿真分析表明.相对于位移模态,应变模态对损伤更为敏感。利用模态叠加方法可获得车体应变、应力时间历程,为疲劳寿命预测及栽荷谱研究提供依据。
关键词:轨道车辆;车体;损伤诊断;应变模态;强度
中图分类号:U270.1+1文献标志码:A 文章编号:2095-5383(2019)03-0016-05
为了保证高速动车组车辆运行的安全性及可靠性,对结构进行强度设计及疲劳寿命预测是其结构设计的重要内容。强度设计及疲劳寿命预测都与结构应力有关,但结构应力不能通过测量直接获得,而是通过应力、应变及位移之间相互关系,通过测量位移或应变的方式获得。采用位移模态分析方法可以建立动车组结构位移响应模型,进行结构振动响应等分析;通过位移——应变的计算得到车体响应的应变模态。但是,从位移到应变是微分过程,位移的误差将会得到放大,从而带来误差。
为此,国内外学者致力于将位移模态方法应用到应变模态场中,直接获得结构应变模态。Hillary等等用电阻应变计对应力——应变传递函数进行测量,提出了应变模态的概念。Li等、Bernasconi、Yam等等运用位移模态的微分运算方法来推导和论述应变模态理论。Tsang、李德葆等运用有限元方法来验证应变模态理论,并采用计算仿真和试验测试进行比较验证,李德葆等还论证了应变模态的正交性。赵媛、Lu等运用柔度差、柔度曲率及改进的多位置损伤定位置信准则等三种方法分析了简支梁结构多位置损伤时的定位方法,并比较了三种方法的优缺点。张则荣等运用有限元方法建立振动筛的模型,通过分析发现应变模态对结构损伤更敏感,据此构建了应变模态变化率的结构损伤诊断方法,进而预测结构在产生裂纹及裂纹扩展时的剩余寿命。上述研究构建了完整应变模态理论,应用在结构损伤诊断及应变模态测试方面,但主要应用于形状规则的板、梁等构件,将应变模态理论应用于复杂结构,进行的应力互推及故障诊断的较少。
本文从应变模态理论构建出发,通过某型动车组车体模型位移模态和应变模态进行仿真对比分析,验证应变模态对结构改进及损伤的敏感性;通过获得车体结构应变模态,可研究关心位置例如车窗附近的应变,为结构应力集中、局部结构改进对变动区域附近的影响、车体结构健康检测等研究提供依据;通过应变模态及试验,获取车体关心位置处应力,为结构疲劳寿命计算及载荷谱研究提供依据。
1应变模态理论
2动车组车体应变模态分析
车体结构采用大型中空铝合金挤压型材焊接而成,由于结构设计需要,需要安装车窗、车门等结构,因而这些位置处易产生应力集中,也是最易产生结构疲劳破坏的位置。应变模态相对于位移模态对于局部结构改动引起的应力变化及局部损伤更加敏感,可通过数值仿真的方法对此予以分析。
文献[9-12]的研究表明,应变模态及其差分曲线研究可以作为车体结构强度计算及损伤定位诊断的有效方法。然而,车体实际上是结构复杂的焊接结构,其强度计算及损伤定位诊断远比等效截面模型复杂。因此,利用车体结构有限元模型,提取车体关心部位位移模态与应变模态,利用应变模态方法分析车体结构强度,为车体设计及疲劳强度分析提供依据。
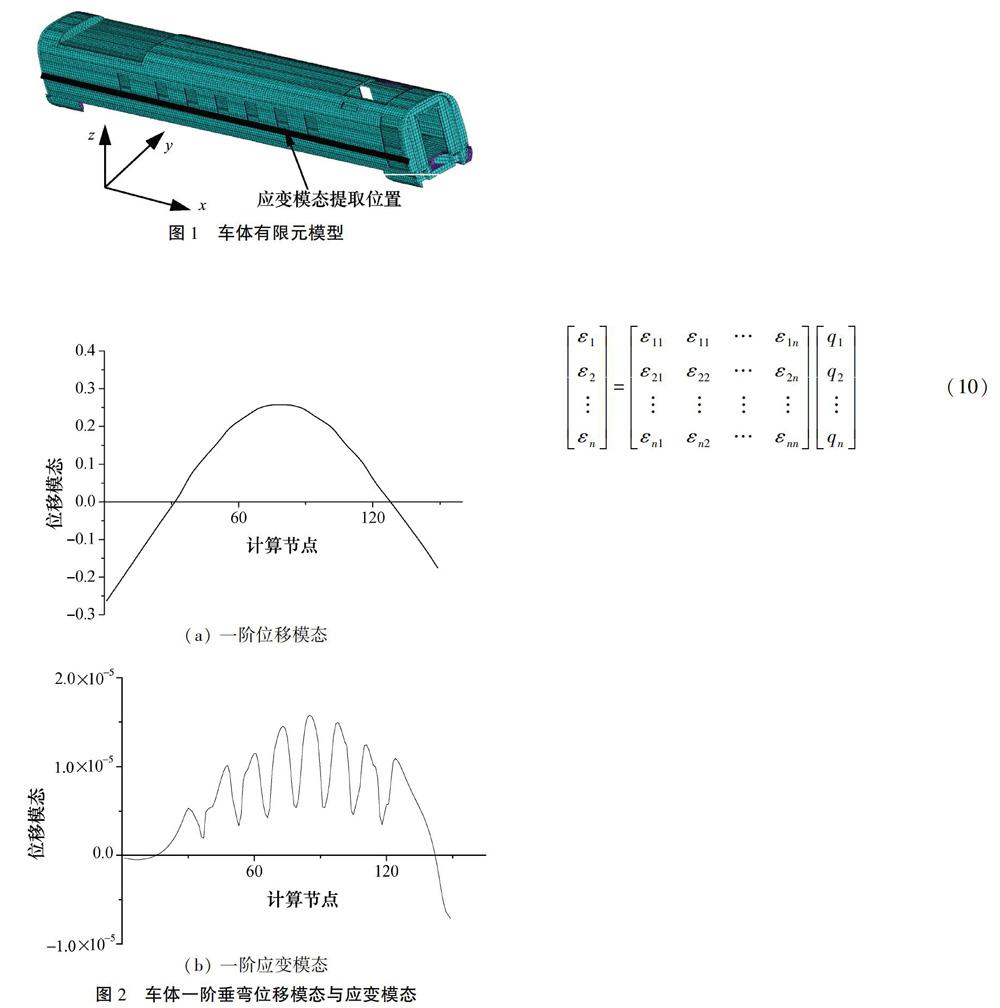
高速列车车体主要采用大型中空宽幅铝合金挤压型材焊接而成,由底架、车顶、端墙和侧墙组成,首先采用不同形状的双面中空铝合金挤压型材焊接成部件,再将各部分焊接成完整的车体,除此之外,车体内装及车下设备也必须考虑。某型动车组车体有限元模型,如图1所示,将模型网格划分为49503个节点,82527个单元。
车体x轴方向车窗下沿位置处一阶垂弯位移模态与应变模态,如图2所示。
从图2可以看出,沿车体纵向轴线方向上,位移模态曲线连续变化,无明显突变,表明车体结构位移模态对于车窗等结构变化不敏感,由位移模态计算得到的结构强度也不会反映车窗结构对车体强度的影响。由于所提取位置处车体x方向结构的非对称性,其模态曲线也是非对称曲线。而车窗位置处应变模态产生较大变化,表明车窗结构对车体结构应变影响较大,在车窗开口位置处,车体x向应变模态降低,两个车窗连接位置处x向应变模态增大,在车体长度方向上应变交替变化,表明车体强度在车窗位置处产生交替变化。由式(9)可知,车体在该位置处会出现应力变化,易出现应力集中、强度不足等结构缺陷,在结构设计中应予以足够重视。
考虑车体垂向振动时,车体的应变可以表示为前n阶应变模态的线性叠加.因此在获取车体结构前n阶应变模态后,根据模态叠加原理,可求得车体关注位置的应变。在提取车体上n个测点的前n阶应变模态,每个点的前n阶应变模态组成一行,n个点就可组成n×n矩阵[εij],构成应变模态叠加法中的应变振型向量。设应变模态坐标为[qi],车体应变[εi]可表征为:
由于应变振型向量是应变的相对值,而模态坐标无法直接求取,可采用应变模态分析与应变测试相结合的方法获得模态坐标[qi]。具体为:在想要获得应变位置处布置应变片,通过应变片测试获得某一点的应变;同时,通过有限元分析提取该点前n阶应变模态,通过公式(10)即可求得应变模态坐标[qi]。获得应变模态坐标后,在应变模态分析结果中提取其他点的前n阶应变模态,由应变模态向量矩阵和應变模态坐标矩阵相乘即可求出其他对应点的应变。
3车体应力推断方法
在高速列车车体设计中,强度设计是车体设计的重要内容,由于车体结构复杂,考虑因素较多,基于应变模态的车体强度设计及损伤诊断为车体设计提供了一种新方法。对于车体而言,应用应变模态求取车体结构应变,根据胡克定律得到模态应力场,应力响应可通过模态叠加法来表示,有了应力响应后即可求得主应力,进而可以进行车体强度设计。
考虑车体垂向振动时,车体的应力以x方向上的轴向应力为主,其应力与应变的关系简化为:
σ=Eε(11)
式中:σ为车体应力,E为弹性模量,ε为车体应变。
通过提取n个测点的一段应变时间历程,根据模态叠加法计算对应的随时间变化的系数矩阵,再将车体上其他点的前n阶应变模态与系数矩阵相乘,即可计算出车体上任意一点的应变时间历程。根据上式可得应力时间历程,从而可进行车体强度设计。
在线路随车试验中,通过传感器也可直接获得应力数值,因此可直接采用应力模态叠加的方法,获得车体结构的应力时间历程。
选取车体动应力测试位置,如图3所示。具体为车窗开口位置处,在车体表面位置处共有15个测点。测试前,在测试位置处粘帖应变片,通过端子將应变片与引线相连,采用安捷伦数据采集系统,实现大容量、高采样频率采集数据。试验测试采样频率为250Hz,增益为64倍,滤波频率为10Hz,应用安捷伦数据采集系统采集到的数据为电压信号,并生成1个二进制文件,将此二进制文件按照采集通道数分离,即可得到各测点的数据。
用有限元软件ANSYS对车体进行模态分析,提取车体前8阶模态应力,根据线路测试结果得到各点应力时间历程,通过计算可获得车体各阶模态坐标,进而可获得车体表面任意一点应力时间历程。为了验证本方法,本文选取车体靠近车窗位置处测点C59、C121、C104、C72、C42、C84、C91、C79应力为已知应力,推断测点C87、C112、C69、C113、C89、C77、C124处应力时间历程,并与实测的应力时间历程对比。
在模态分析结果中,提取了车体上15个测点的前8阶模态应力,如表1所示。
依据模态叠加法,根据前节所述方法,可得C87、C112、C69、C113、C89、C77、C124处应力时间历程。C69、C124测点计算应力时间历程和实测应力时间历程曲线,如图4所示。可以看出其计算应力时间历程和实测应力时间历程变化趋势相同,考虑到有限元建模误差,以及对车体的约束设置与实际运行列车不一致性,导致两者之间有偏差,最大偏差在0.03MPa,最大偏差相对值为15%,与实测值有较好的一致性。
4结论
本文应用车体有限元模型,分析了车体有限元模型的位移模态和应变模态,研究了应变模态在应变和应力获取方面的应用,提出了车体强度设计及疲劳寿命的新方法,主要结论如下:
1)应变模态与位移模态是同一能量平衡状态的两种表现形式.应变模态也可通过应变模态振型和模态坐标叠加求解。
2)相比于位移模态,应变模态对结构损伤更具敏感性,通过车体有限元模型验证了这一结论。
3)对于车体这类复杂结构,其强度设计是结构设计的重要内容,基于应变模态的车体应变及应力计算方法有一定的适用性及可行性,可为车体疲劳强度分析及载荷谱研究提供依据。
