基于LSTM循环神经网络的电池SOC预测方法

耿攀 许梦华 薛士龙

摘要：针对锂离子电池荷电状态（state of charge， SOC）预测问题，利用长短期记忆（long short-term memory， LSTM）循环神经网络建立电池SOC预测模型。在恒阻放电情况下，将电池输出电流、输出电压和电池表面温度作为模型的主要输入，使用训练样本对神经网络进行训练，使用验证样本进行验证。结果表明，用该方法进行电池SOC预测时可使最大绝对误差仅为1.96%，均方根误差为0.986%，可行性被验证。分析神经网络隐含层中不同的神经元个数对预测结果的影响，对比不同批大小情况下训练出的神经网络的预测误差。将隐含层分别设置为1至3个LSTM细胞核，得到不同条件下神经网络的预测误差。结果为电池SOC预测的神经网络模型的隐含层神经元个数、批大小和LSTM细胞核个数的设定提供参考。

关键词：锂离子电池; 荷电状态（SOC）; 电动汽车; 长短期记忆（LSTM）; 循环神经网络

中图分类号： TM911

文献标志码： A

Abstract：For the estimation problem of lithium-ion battery state of charge （SOC）， a model of battery SOC estimation is established by the long short-term memory（LSTM） recurrent neural network. When the battery is discharging in constant-resistance circumstances，the output current， the output voltage and the surface temperature of the battery are used as the main inputs of the model， and the neural network is trained with training samples and verified with verification samples. The results show that the maximum absolute error is only 1.96% and the root mean square error is 0.986% when the battery SOC is estimated by this method， which validates the feasibility of the method. The effects of different number of neurons in the hidden layer of the neural network on the estimation results are analyzed， and the estimation errors of the neural network trained under different batch sizes are compared. The hidden layer is set to 1 to 3 LSTM nuclei， respectively， and the estimation errors of the neural network under different conditions are obtained. The results can provide reference for the setting of the number of neurons in the hidden layer and the batch size of the neural network model for estimating battery SOC and the setting of the number of LSTM nuclei.

0 引 言

鋰离子电池以能量密度高、使用寿命长、自放电率低等优点在电动汽车上被广泛应用。锂离子电池荷电状态（state of charge，SOC）为能量管理和控制策略的主要依据，因此准确估计电池的SOC对电池的高效利用和整车能量管理具有重要意义[1]。

目前常用的SOC预测方法分为3类：第一类直接根据电池的电压、电流或内阻进行预测，主要方法包括安时积分法[2]，开路电压法[3]和基于电池内阻[4]的预测法;第二类是基于等效电池模型的预测法，如滑模观测器[5]和龙贝格观测器[6];第三类是近五年发展的基于机器学习的预测方法，主要包括支持向量机[7-8]、极限学习机[9]、径向基神经网络[10]和循环神经网络[11]等方法。

安时积分法通过先测量电流再对电流进行积分实现电池SOC预测，但无法解决累积误差和不准确的电池SOC初始值问题[12];开路电压法的缺点是预测前需要电池长时间静置，不适合在线测量[13];基于电池内阻的预测法受电池种类、数量和一致性的影响，很少在电动汽车上使用[14]。

等效电池模型一般采用等效电阻电容模拟电池的动态响应，但忽略了电池单元内部的物理和化学反应，当电池处于过充过放等会导致剧烈物理和化学反应的状态时，等效电路模型往往无法反映真实电池模型[13]。另外，这种方法计算量大，实际应用中在不同环境下预测电池SOC需要额外的参数或者不同的电池模型。文献[14]采用优化电池模型的自适应sigma卡尔曼算法预测电池SOC，但只是在一定程度上减少了电池模型的复杂度和计算量。同时，灰色扩展卡尔曼滤波[15]、平方根无迹卡尔曼滤波[16]等改进算法被提出，此类卡尔曼滤波算法都依赖高精度的电池模型，计算复杂[17]。

研究人员也曾使用涉及数据分析的第三类方法进行电池SOC预测，这些方法依赖于传统的机器学习技术：文献[18]使用了支持向量机进行预测，文献[9]使用了极限学习机进行预测，传统的机器学习技术有着共同缺陷，即训练速度慢且容易陷入局部最小点[19]。针对上述三类方法存在的缺陷，本文使用具有长短期记忆（long short-term memory， LSTM）[20]细胞核的循环神经网络（称为LSTM循环神经网络）使SOC预测的绝对误差降至2%以下。

近年来，随着深度学习技术的不断发展，一些深度学习模型逐渐被应用到时序数据的研究中。深度学习模型是一种拥有多个非线性映射层级的深度学习神经网络模型，能够对输入信号逐层抽象并提取特征，挖掘出更深层的潜在规律。现实生活中，搜索引擎的内容筛选过滤、社交媒体个人喜好分析推荐以及各种可携带智能设备的自然语言处理等都使用了深度学习。这些成功的深度学习应用案例使用的预测方式都可以归结为人工神经网络的一个分支，被称作LSTM循环神经网络。

LSTM循环神经网络作为一种新型机器学习技术，可以通过自身学习调整网络权重和偏置等参数实现电池SOC的预测。这项技术可以将测量所得的各种信息，比如电压，电流、电池表面温度等准确地映射到电池SOC，并且有效避免如卡尔曼滤波算法繁冗的参数推算过程，在训练过程中只需设置隐含层神经元个数、批大小、最大迭代次数和LSTM细胞核个数便可以获得最优模型。利用LSTM循环神经网络可以在不同工况环境下、不同输入参数变量下甚至不同电池种类下得出不同的网络参数模型，这一过程只需对不同种类电池采样获得一定量的训练数据。

1 LSTM循环神经网络模型

循环神经网络与BP神经网络或者其他常规的机器学习神经网络不同，常规的神经网络都是将当前时刻的输入参量输入获得当前时刻的输出，循环神经网络能够将前一段时刻的一系列信息传递给当前时刻。循环神经网络标准模型及其展开模型如图1所示（RNN表示循环神经网络）：在输入端输入一个序列X=（x1，x2，…，xt），通过式（1）计算出一个隐含层序列H=（h1，h2，…，ht），再通过式（2）计算出一个输出序列Y=（y1，y2，…，yt）。

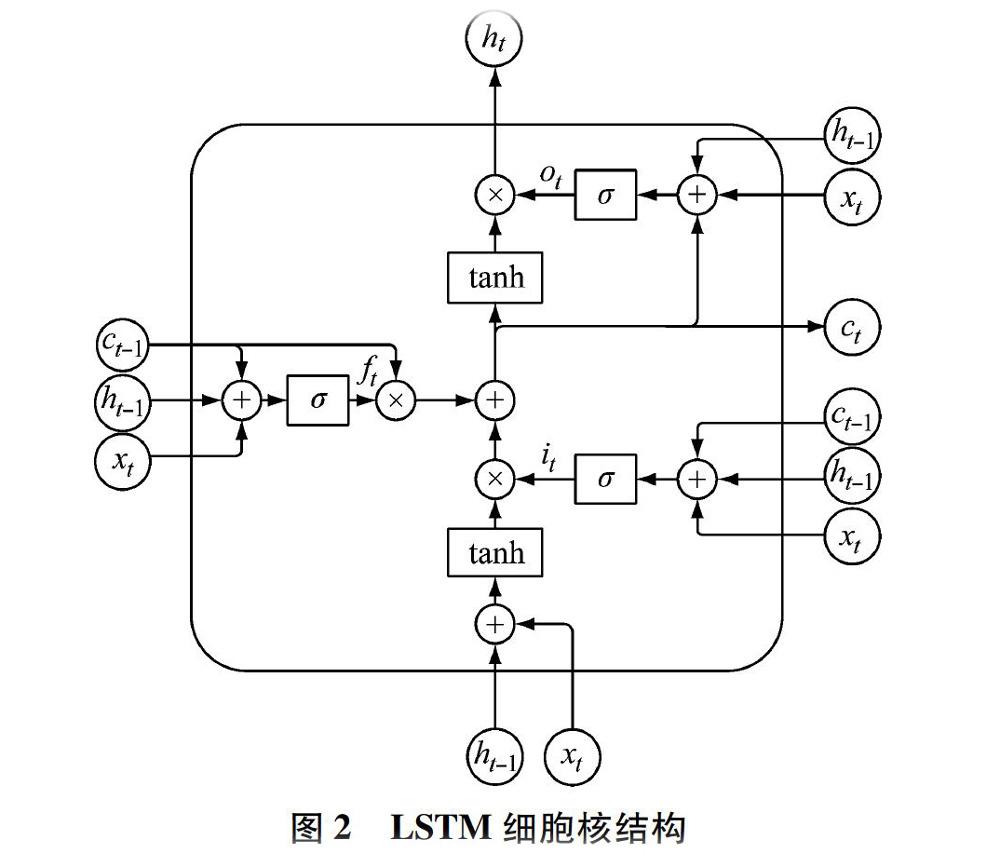
循环神经网络虽然可以有效地处理非线性时间序列，但随着时间的不断拉长，会产生一系列问题，比如梯度下降或者梯度爆炸，这会导致前期的有效信息丢失或者产生无效信息，从而预测错误。为此，将传统循环神经网络的循环神经网络细胞核替换成LSTM细胞核，使其具有长期记忆能力，从而成功地解决长期大量数据上的预测问题。LSTM细胞核结构见图2。

在LSTM细胞核中，ct是LSTM的状态单元，贯穿于整个细胞，LSTM细胞能够向状态单元填充有效信息或者移除无效信息，这一过程中使用的结构被称为门限。门限由一个sigmoid函数与矩阵点乘组成，sigmoid函数输出0-1之间的数字，描述每个信息通过门限的程度，0表示禁止一切信息通过，1表示所有信息通过。整个LSTM细胞中有3个门限，分别为遗忘门f、输入门i和输出门o。LSTM循环神经网络前向传播可以表示为式中：σ和tanh分别为sigmoid激活函数和双正切激活函数;it、ft、ot、ct分别代表t时刻输入、忘记、输出和细胞状态。基于LSTM循环神经网络的电池SOC预测模型训练框架（见图3）包含輸入层、隐含层和输出层：输入层用于表征输入变量，隐含层可以是一个或多个LSTM细胞核，输出层用于表征输出变量。全连接层根据权重W与偏置b组合实现隐含层线性输出ht，ht再经过输出层可得到t时刻的输出值。设隐含层的初始状态矩阵为全零矩阵。

如图3所示，当LSTM循环神经网络进行前向传播后，网络输出值与真实值之间的误差计算式为式中：T表示为预测电池SOC选取的序列长度;yt和y*t分别表示t时刻电池SOC的预测值和真实值。在每次迭代中，LSTM循环神经网络都会进行反向传播，用Adam优化方法[21]更新网络权重和偏置：

式中：mε和γε分别为第ε时间步时的初始L1、L2正则化衰减矩阵;ε和ε分别为mε和γε更新后的矩阵;衰减因子β1和β2通常在0.900至0.999之间取值;学习速率α一般设置为0.000 1;常数θ=1×10-8;Wε为权重矩阵。当达到最大迭代次数后网络训练结束，此时将训练好的模型保存，并挑选出符合性能要求的网络模型供预测使用。

2 实验测试与数据预处理

2.1 实验测试

本文采用与特斯拉电动汽车相似的电池单元——松下公司生产的NCR18650PF锂离子电池作为实验对象，该电池单元参数如下：电池质量47.5 g，额定电压3.6 V，额定电池容量2.9 A·h，额定内阻35 mΩ，最大充电电压4.2 V，放电截止电压2.5 V，放电温度-20～60 ℃。

建立的单节电池充放电实验测试台如图4所示，主要由单节锂离子电池、Chroma充电仪、WT1600功率仪和温度传感器构成：Chroma充电仪可按照设定电压、电流对电池进行充电;WT1600功率仪可实现对电池电压、电流的采集功能。所有实验均在室温下进行。

为获取电池放电数据用以训练和验证LSTM循环神经网络，电池以4.2 V/2.9 A充电模式进行充电，如果电池电压保持在4.2 V，充电电流降至50 mA，则表示电池已充满。充电结束后，将电池在室温下静置1 h，接0.5 Ω电阻对电池恒阻放电，记录放出电量;如果电池电压下降至2.5 V则表示电池电量全部放完;将电池再次静置1 h，重新进行充放电实验，并记录数据;在室温环境下，对电池重复充放电5次，获得5组数据。这5组数据显示的电池在放电阶段的电压、电流及其表面温度变化曲线见图5。

选取其中4组数据作为LSTM循环神经网络的训练集，剩下的1组作为测试集。WT1600功率仪的误差为±0.1%，精确度很高，可利用WT1600功率仪获得电池真实SOC值。将基于LSTM循环神经网络模型的预测结果与真实值进行比较。采用统计误差评估LSTM循环神经网络预测模型的性能，统计误差包括均方根误差，平均绝对误差和最大绝对误差，计算式分别如下：

2.2 数据预处理

通过适当的数据预处理，可以使网络的训练数据更加有效和稳健。使用算术平均滤波法让每组原始数据平滑化，再归一化所有数据，提高网络模型训练时的收敛速度。利用下式把输入和输出数据归一化到0与1之间：

式中：xmax和xmin是LSTM循环神经网络输入数据x的最大值和最小值。

3 实验结果分析

如前所述，Xt为第t时刻神经网络的输入序列，Xt=（Vt，It，Tt），其中Vt为电池电压，It为电池电流， Tt为电池表面温度。经过训练后，神经网络可自学得到整个网络参数，见图6。

设置LSTM循环神经网络为单个LSTM细胞核，隐含层神经元个数n为320，批大小为200，最大迭代次数为200，用4组数据去训练神经网络，总用时117 s。得到的模型用剩下的1组数据进行验证，得到预测结果的均方根误差、平均绝对误差和最大绝对误差分别为0.986%、0.455%和1.96%，预测值与真实值偏离程度很小，因此可以确定能够使用LSTM循环神经网络建立电池SOC预测模型，该预测模型的性能见图7。

3.1 神经网络超参数设定对预测结果的影响

隐含层神经元个数n、批大小是LSTM循环神经网络重要的超参数，其中批大小为一次训练的样本数目，它将整个样本分为若干个小批次输入神经网络，这2个超参数的设定对模型预测精度有重要影响。

设置隐含层为单个LSTM细胞核，批大小为512，最大迭代次数为200，隐含层神经元个数分别为80、260和440。在隐含层神经元个数n不同的情况下，选择神经网络总训练时间、均方根误差、平均绝对误差和最大绝对误差对模型预测结果进行评价，见图8和9。

随着隐含层神经元个数n的增加，预测模型的训练时间增加，虽然平均绝对误差和均方根误差呈现下降趋势，但整体来说隐含层神经元个数的增加对这两种误差的减少并没有太大作用;随着隐含层神经元个数n的增加，最大绝对误差下降较明显，当n=80时最大绝对误差大于6%，当n=440时最大绝对误差小于4%。为实现预测模型的准确可靠性，同时考虑模型训练时间，应适当增加隐含层神经元的个数。

为验证批大小对预测结果的影响，设置隐含层为单个LSTM细胞核，隐含层神经元个数n为200， 最大迭代次数为200，批大小分别取200、356和512，不同批大小情况下训练出的LSTM循环神经网络预测结果和预测误差见表1和图10。

由表1可知：当批大小增大时，网络总训练时间会减少;批大小的增加会使最大绝对误差变大，但使均方根误差和平均绝对误差减小，提高了网络预测的整体精度。为减少网络总训练时间，应当增大批大小，但又考虑到预测结果的最大绝对误差限制，不能将批大小增至过大，否则预测结果的最大绝对误差超过5%，导致预测结果不准确。

3.2 LSTM细胞核个数对预测结果的影响

为体现多个LSTM细胞核对预测结果的影响，在隐含层分别设计1、2、3个LSTM细胞核，每个LSTM细胞核的神经元个数为320，批大小为400，最大迭代次数为200，分析对比在隐含层中LSTM细胞核个数不同时的预测结果和预测误差，见图11。

a）预测结果

b）预测误差

LSTM隐含层被设计有1个或2个LSTM细胞核时，都能保证预测误差在4%以下;当隐含层被设计有3个LSTM细胞核时，预测误差较大，在电池SOC到达40%后，预测误差大于5%，不能实现准确预测。因此，隐含层LSTM细胞核个数应该小于3个，以防止训练出来的预测网格出现过拟合情况，从而不能达到良好的预测效果。

4 结 论

针对锂离子电池荷电状态（SOC）预测问题，提出了基于LSTM循环神经网络的锂离子电池SOC预测方法。本文主要解决了4个问题：解决了以往电池SOC预测的电池物理建模问题，利用LSTM循环神经网络将电池相关测量值（电压、电流和表面温度）直接映射到电池SOC;让研究人员从人工计算电池模型参数或者预测算法（如卡尔曼滤波算法）参数中解放出来，LSTM循环神经网络可利用收集得到的原始数据训练神经网络自学习所有网络参数;电池SOC预测精度提高，即通过实验验证，所建立的预测模型最大绝对误差小于2%，低于实际应用要求的5%，满足实际应用要求;关于基于LSTM循环神经网络的电池SOC预测模型的设计问题，通过对比LSTM循环神经网络神经元个数、批大小这2个重要超参数以及LSTM细胞核个数对预测误差的影响可得到，在保证预测精度的前提下，LSTM循环神经网络神经元个数、批大小不宜过大，LSTM细胞核个数应该小于3个，以防止训练出来的预测模型出现过拟合情况。总之，LSTM循环神经网络经过实验验证并获得了良好的性能。事实证明，它是锂离子电池SOC预测的强大工具，也可能是未来工作中可能考虑的其他电池的诊断策略。鉴于能量存储系统产生的数据量，考虑用机器学习算法来执行状态和参数估计是很自然的，本文展示了这些算法是如何自学来预测模型的参数的，讨论并研究了LSTM循环神经网络用于电池SOC预测时网络超参数和细胞核个数的设定方式，即使暴露在稀缺的数据集中，也能实现竞争性评估绩效。

参考文献：

[1]费亚龙， 谢长君， 湯泽波， 等. 基于平方根无迹卡尔曼滤波的锂电池状态估计[J]. 中国电机工程学报， 2017， 37（15）： 4514-4520. DOI： 10.13334/j.0258-8013.pcsee.161687.

[2]于海芳， 逯仁贵， 朱春波， 等. 基于安时法的镍氢电池SOC估计误差校正[J]. 电工技术学报， 2012， 27（6）： 12-18. DOI： 10.19595/j.cnki.1000-6753.tces.2012.06.003.

[3]WENG Caihao， SUN Jing， PENG Huei. A unified open-circuit-voltage model of lithiumion batteries for state-of-charge estimation and state-of-health monitoring[J]. Journal of Power Sources， 2014， 258（14）： 228-237. DOI： 10.1016/j.jpowsour.2014.02.026.

[4]李革臣， 古艷磊. 电化学阻抗谱法预测锂电池荷电状态[J]. 电源技术， 2008， 32（9）： 599-602.

[5]孙东， 陈息坤. 基于离散滑模观测器的锂电池荷电状态估计[J]. 中国电机工程学报， 2015， 35（1）： 185-191. DOI： 10.13334/j.0258-8013.pcsee.2015.01.023.

[6]WAAG W， FLEISCHER C， VIEJO C B， et al. Critical review of the methods for monitoring of lithium-ion battery in electric and hybrid vehicles[J]. Journal of Power Sources， 2014， 258： 321-339. DOI： 10.1016/j.jpowsour.2014.02.064.

[7]MENG Jinhao， LUO Guangzhao， GAO Fei. Lithium polymer battery state-of-charge estimation based on adaptive unscented Kalman filter and support vector machine[J]. IEEE Transactions on Power Electronics， 2016， 31（3）： 2226-2238. DOI： 10.1109/TPEL.2015.2439578.

[8]ANTON J C A， NIETO P J G， JUEZ F E D C， et al. Battery state-of-charge estimator using the SVM technique[J]. Applied Mathematical Modeling， 2013， 37（9）： 6244-6253. DOI： 10.1016/j.apm.2013.01.024.

[9]DU Jiani， LIU Zhitao， WANG Youyi. State of charge estimation for Li-ion battery based on model from extreme learning machine[J]. Control Engineering Practice， 2014， 26： 11-19. DOI： 10.1016/j.conengprac.2013.12.014.

[10]CHANG Wen-Yeau. Estimation of the state of charge for an LFP battery using a hybrid method that combines an RBF neural network， an OLS algorithm and AGA[J]. International Journal of Electrical Power and Energy Systems， 2013， 53： 603-611. DOI： 10.1016/j.ijepes.2013.05.038.

[11]CHAOUI H， IBE-EKEOCHA C C. State of charge and state of health estimation for lithium batteries using recurrent neural networks[J]. IEEE Transactions on Vehicular Technology， 2017， 66（10）： 8773-8783.

[12]MEJDOUBI A E， OUKAOUR A， CHAOUI H， et al. State-of-charge and state-of-health lithiumion batteries diagnosis according to surface temperature varoation[J]. IEEE Transactions on Industrial Electronics， 2016， 63（4）： 2391-2402. DOI： 10.1109/TIE.2015.2509916.

[13]CHEN Lin， WANG Zhengzheng， LU Zhiqiang， et al. A novel state-of-charge estimation method of lithiumion batteries combining the grey model and genetic algorithms[J]. IEEE Transactions on Power Electronics， 2017， 33（10）： 8797-8807. DOI： 10.1109/TPEL.2017.2782721.

[14]刘毅， 谭国俊， 何晓俊. 优化电池模型的自适应Sigma卡尔曼荷电状态估算[J]. 电工技术学报， 2017， 32（2）： 108-118.

[15]潘海鸿， 吕治强， 李君子， 等. 基于灰色扩展卡尔曼滤波的锂离子电池荷电状态估算[J]. 电工技术学报， 2017， 32（21）： 1-8. DOI： 0.19595/j.cnki.1000-6753.tces.160837.

[16]AUNG H， LOW K S， GOH S T. State-of-charge estimation of lithiumion battery using square root spherical unscented Kalman filter （Sqrt-UKFST） in nanosatellite[J]. IEEE Transactions on Power Electronics， 2015， 30（9）： 4774-4783. DOI： 10.1109/TPEL.2014.2361755.

[17]SHENG Hanmin， XIAO Jian， WANG Peng. Lithium iron phosphate battery electric vehicle state-of-charge estimation based on evolutionary Gaussian mixture regression[J]. IEEE Transactions on Industrial Electronics， 2017， 64（1）： 544-551. DOI： 10.1109/TIE.2016.2606588.

[18]ANTON J C A， NEITO P J G， VIEJO C B， et al. Support vector machines used to estimate the battery state of charge[J]. IEEE Transactions on Power Electronics， 2013， 28（12）： 5919-5926. DOI： 10.1109/TPEL.2013.2243918.

[19]王琪， 孙玉坤， 倪福银， 等. 一种混合动力电动汽车电池荷电状态预测的新方法[J]. 电工技术学报， 2016， 31（9）： 189-196. DOI： 10.3969/j.issn.1000-6753.2016.09.024.

[20]HOCHREITER S， SCHMIDHUBER J. Long short-term memory[J]. Neural Computation， 1997， 9（8）： 1735-1780.

[21]KINGMA D P， BA J L. Adam： a method for stochastic optimization[C]//3rd International Conference for Learning Representations， San Diego， 2015. arXiv：1412.6980[cs.LG]. https：//arxiv.org/abs/1412.6980.

（編辑 赵勉）