基于调和分析和ARIMA-SVR的组合潮汐预测模型

刘娇 史国友 朱凯歌 张加伟 李爽 陈作桓 王伟

摘要：为提高潮汐预测精度，解决单一调和分析预测精度不高的问题，提出一种基于调和分析和自回归综合移动平均-支持向量回归机（autoregressive integrated moving average support vector machine for regression，ARIMA-SVR）的组合潮汐预测模型。潮汐分析中，潮汐可认为是由受引潮力影响的天文潮位和受环境因素影响的非线性水位的叠加。采用小波分析对潮汐样本数据进行去噪处理，使用调和分析法计算天文潮位，以调和分析法计算产生的残差作为非线性水位样本数据，并使用ARIMA-SVR模型进行潮高计算，最后将两部分的计算结果进行线性求和得到最终的潮汐预测值。利用美国旧金山港口实测潮汐数据进行预测仿真，结果表明，该组合模型解决了调和分析忽略非线性影响的问题，提高了潮汐预测准确率，可行且高效。

关键词：潮汐预测; 组合模型; 调和分析法; 支持向量回归机（SVR）; 自回归综合移动平均（ARIMA）模型

中图分类号： U675.12

文献标志码： A

Abstract：To improve the accuracy of tide prediction and solve the problem of low accuracy of single harmonic analysis， a combined tide prediction model based on the harmonic analysis and the autoregressive integrated moving average-support vector machine for regression （ARIMA-SVR） is proposed. In tide analysis， tide can be considered as the superposition of astronomical tide level affected by tide-generating force and non-linear water level affected by environmental factors. The wavelet analysis is used to denoise the tide sample data. The harmonic analysis method is used to calculate the astronomical tide level. The residual sequence generated by the harmonic analysis method is used as the sample data of non-linear water level， and ARIMA-SVR model is used to calculate the tide height. The tide prediction value is obtained by linear summation of the calculated results of the two parts. The simulation of prediction is carried out using measured tide data of San Francisco Port of the United States. The results show that： the combined model solves the problem of ignoring nonlinear effects in the traditional harmonic analysis， and the accuracy of tide prediction is improved; the combined model is feasible and efficient.

0 引 言

潮汐是海平面周期性的升降运动，它的涨落与人们的生产生活有着密切的联系。实时精准的潮位信息在船舶航行安全、海洋资源开发利用、海洋灾害的减轻与预防中发挥着举足轻重的作用。因此，研究一种简单、高效的潮汐预测方法成为亟待解决的问题。现有的潮汐预测方法主要分为传统预测模型和智能化预测模型。

传统潮汐预测模型主要是用调和分析法进行预测的。Thomson于1866年首次将调和分析法应用于潮汐预测中，Darwin对该方法做了进一步完善，创立了典型的平衡潮理论。Doodsen利用最小二乘法来确定调和分析常数。Yen将卡尔曼滤波应用于确定有限实测潮汐数据的调和分析常数。经过上百年的积淀，调和分析法在潮汐预测中已经得到广泛的应用，但该模型仅考虑了受引潮力影响的线性系统，忽视了受风力、气压、海底地形等环境因素影响的非线性系统。非线性系统受环境影响波动较大，如果用调和分析法预测会产生较大误差。

随着人工智能时代的到来，越来越多的智能化模型被应用于数据预测领域。神经网络由于具备较强的自适应学习能力和非线性映射能力，已经被广泛地应用于潮汐预测。不少学者将神经网络与相关智能算法相结合，建立了潮汐预测模型，取得了较大的进展。TSAI等[1]第一次将人工神经网络模型运用到全日潮和半日潮的预测中;LIN等[2]在考虑了潮汐力和海洋热膨胀后，提出了一种自适应神经模糊推理系统，用于海平面的预测;JAIN等[3]利用神经网络建立了预测步长为24 h的潮汐预測模型，并将此应用于印度洋西海岸New Mangalore潮位站。然而，神经网络存在一定的缺陷，如需要大量的训练数据、易陷入局部最优、不具备良好的泛化性等。由于实现了结构风险最小化（structural risk minimization，SRM），对未来样本具有极强的泛化能力，支持向量回归机（support vector machine for regression，SVR）现已被广泛应用于时间序列预测领域。孟二浩[4]已将SVR成功应用于月径流量的预测;唐军等[5]提出了一种基于最小二乘支持向量机的在线交通流预测模型，利用数据集滑动时间窗口控制新样本点的加入。SVR在潮汐预测中应用较少，因此在该领域具有广阔的研究前景。

基于此，本文提出一种基于调和分析法和自回归综合移动平均-支持向量回归机（autoregressive integrated moving average SVR，ARIMA-SVR）的组合潮汐预测模型。该模型在调和分析法预测的基础上，对预测产生的残差序列，使用ARIMA和SVR进行处理预测，充分利用天文潮位和非线性水位两部分的数据信息，提高潮汐预测的准确率。利用美国旧金山港口的实测潮汐数据进行预测仿真，结果表明，该组合模型可行且高效。

1 相关概念

1.1 SVM与SVR

支持向量机（support vector machine，SVM）是一种有坚实理论基础的小样本、非线性学习方法，它基于统计学习的VC维和结构风险最小化的原则，以实现模型复杂度、样本学习能力和在样本信息限制下获取最佳泛化能力等3个方面的折中，能够在一定程度上规避“维数灾难”和“过学习”等传统学习困难。SVM主要分为支持向量分类机（support vector machine for classification，SVC）和SVR，分别用于解决分类问题和回归预测问题。

SVR是通过寻找一个非线性变换（x），将输入向量从空间Rn映射到Hilbert高维特征空间，在该空间内进行线性回归。通过映射使训练集T中的每个点（xi，yi）尽量拟合到如下线性模型：

3 结束语

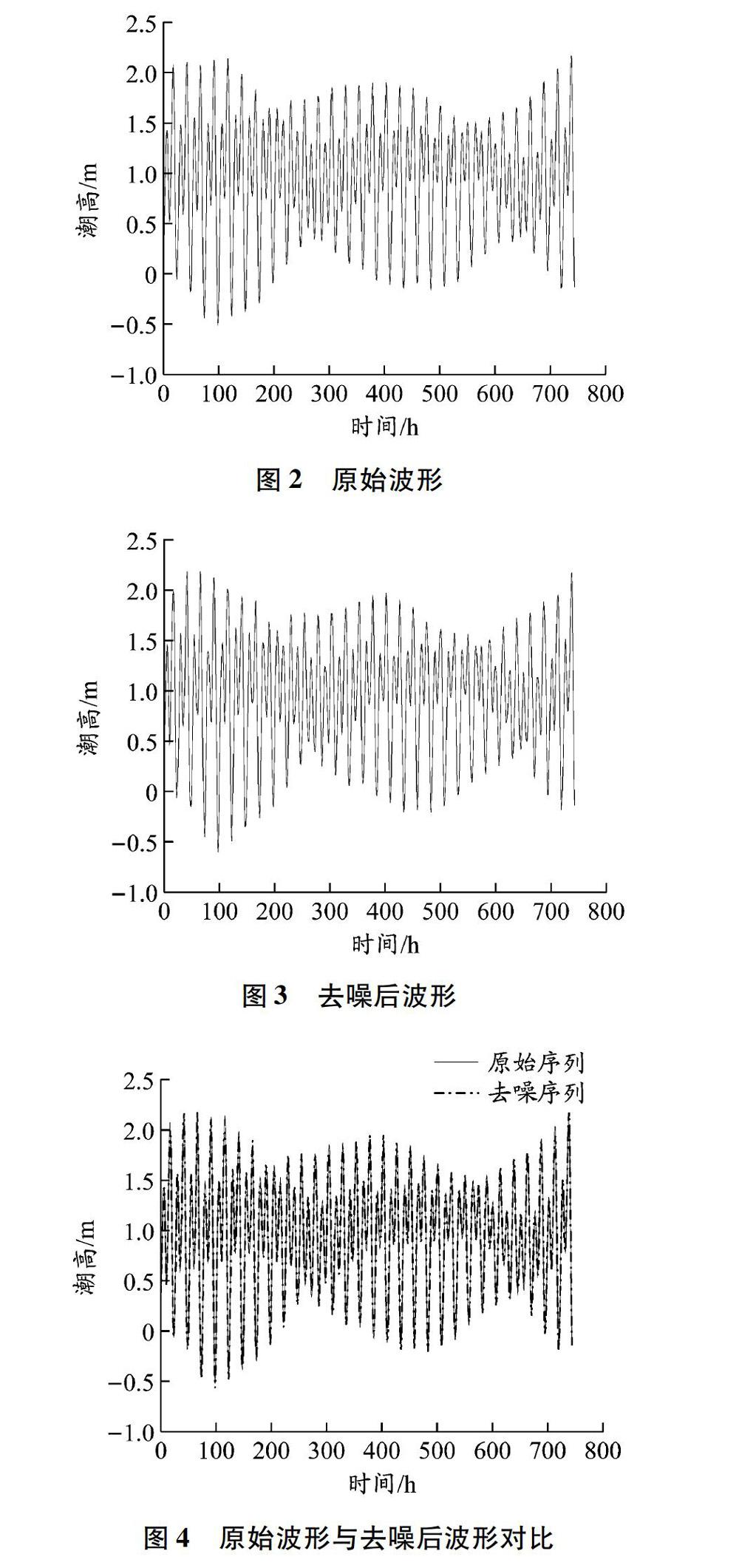
为还原潮汐动力学性质，提高预测准确度，采取小波阈值去噪的方法对潮汐原始数据进行去噪处理。在调和分析预测的基础上，充分利用自回归综合移动平均（ARIMA）模型较强的时间序列处理能力和支持向量回归机（SVR）突出的非线性回归预测能力，提出一种基于调和分析法和自回归综合移动平均-支持向量回归机（ARIMA-SVR）的组合潮汐预测模型，分别用调和分析法和ARIMA-SVR模型计算潮汐天文潮位和非线性水位变化。在非线性水位变化部分，对数据进行归一化处理并使用网格搜寻法进行参数寻优，提高了该部分的预测精度。经实验验证，该模型的预测精度高于组合模型中的任一单一模型以及具有良好的时间序列预测能力的RNN模型，能很好地解决当前单一预测模型的预测精度不高问题，在潮汐预测中具有广泛的应用前景。

参考文献：

[1]TSAI Ching-Piao， LIN Chang， SHEN Jia-N. Neural network for wave forecasting among multi-stations[J]. Ocean Engineering， 2002， 29（13）： 1683-1695. DOI： 10.1016/S0029-8018（01）00112-3.

[2]LIN Li-Ching， CHANG Hsien-Kuo. An adaptive neuro-fuzzy inference system for sea level prediction considering tide-generating forces and oceanic thermal expansion[J]. Terrestrial Atmospheric & Oceanic Sciences， 2008， 19（1/2）： 163-172. DOI： 10.3319/TAO.2008.19.1-2.163（SA）.

[3]JAIN P， DEO M C. Real-time wave forecasts off the western Indian coast[J]. Applied Ocean Research， 2007， 29（1/2）： 72-79. DOI： 10.1016/j.apor-2007.05.003.

[4]孟二浩. 基于改进的EMD混合模型月径流预测研究[D]. 西安： 西安理工大学， 2018.

[5]康军， 段宗涛， 唐蕾， 等. 一种LS-SVM在线式短时交通流预测方法[J]. 计算机应用研究， 2018， 35（10）： 2965-2968.

[6]刘爱国， 薛云涛， 胡江鹭， 等. 基于GA优化SVM的风电功率的超短期预测[J]. 电力系统保护与控制， 2015， 43（2）： 90-95.

[7]甘泽， 李志刚， 张岩. 潮汐发电中调和分析与人工神经网络预测潮位[J]. 河北联合大学学报（自然科学版）， 2014， 36（1）： 84-87.

[8]姚德峰. 基于调和分析的短期潮位粗差探测与修复方法研究[J]. 勘察科学技术， 2016（6）： 28-30.

[9]柳成， 尹建川. 一种高精度的短期潮汐预报模型[J]. 上海海事大学学报， 2016， 37（3）： 74-80. DOI： 10.13340/j.jsmu.2016.03.014.

[10]梁昌勇， 马银超， 陈荣， 等. 基于SVR-ARMA组合模型的日旅游需求预测[J]. 管理工程学报， 2015， 29（1）： 122-127. DOI： 10.13587/j.cnki.jieem.2015.01.016.

[11]柳成. 基于支持向量机的模块化潮汐预报[D]. 大连： 大连海事大学， 2017.

[12]孙映宏， 章国稳， 姬战生. 基于支持向量机的钱塘江潮时预报方法[J]. 水力发电， 2017， 43（7）： 17-21.

[13]张泽国， 尹建川， 柳成， 等. 基于SAPSO-BP网络模型的港口潮汐实时预报[J]. 水运工程， 2017（1）： 34-40. DOI： 10.16233/j.cnki.issn1002-4972.2017.01.006.

[14]ZHANG Zeguo， YIN Jianchuan， WANG Nini， et al. A precise tidal prediction mechanism based on the combination of harmonic analysis and adaptive network-based fuzzy inference system model[J]. Acta Oceanologica Sinica， 2017， 36（11）： 94-105. DOI： 10.1007/s13131-017-1140-x.

（編辑 贾裙平）