Elastic properties of anatase titanium dioxide nanotubes:A molecular dynamics study∗
2019-11-06KangYang杨康LiangYang杨亮ChangZhiAi艾长智ZhaoWang王赵andShiWeiLin林仕伟
Kang Yang(杨康),Liang Yang(杨亮),†,Chang-Zhi Ai(艾长智),Zhao Wang(王赵),and Shi-Wei Lin(林仕伟),‡
1State Key Laboratory of Marine Resource Utilization in South China Sea,Hainan University,Haikou 570228,China
2School of Materials Science and Engineering,Hainan University,Haikou 570228,China
3School of Science,Hainan University,Haikou 570228,China
Keywords:molecular dynamics,elastic properties,TiO2 nanotube,chiral angle,radius
1.Introduction
With the development of science and technology in the past few years,nanostructures have received much attention from many researchers because of their important role in the fields of energy,environment,and production.Among them,titanium dioxide nanotubes(TNTs)have attracted extensive attention.Due to its large specific surface area,high chemical stability,excellent catalytic property,great acid,and alkaline resistance,[1]the TNTs have been widely used in fuel cells,[2,3]photocatalytic systems,[4,5]energy storage devices,[6,7]gassensitive sensors,[8]pH sensors,[9]and other fields. The main preparation methods of titanium dioxide nanotubes are the template-assisted,[10,11]hydrothermal,[12–14]sol–gel,[15]and electrochemical anodization methods.[16,17]However,the TNTs structures prepared by different methods are different from each other and thus present different performances.In order to optimize the composite performance by using TNTs as the addition,the investigation into their elastic and other mechanical properties are of great importance.For example,titanium dioxide nanotubes play an important role in mechanically enhancing bone bonding and epoxy resin.[18,19]However,the elastic and mechanical properties of a single titanium dioxide nanotube are hard to obtain experimentally. Thus,there is still much room for studying the elastic and mechanical properties of titanium dioxide nanotubes.
Like carbon nanotubes,titanium dioxide nanotubes are made of transversely isotropic materials,so they are highly symmetrical in elastic properties and sensitive to the helicity and the radius of nanotubes.[20–22]In order to obtain the elastic properties of TNTs effectively,the elastic constants can be calculated by density functional theory or molecular dynamics. The first principles Vienna ab initio simulation package(VASP)has already predicted the elastic constants of bulk anatase and rutile TiO2at 0 K,[23,24]and the elastic constants of bulk rutile at various temperatures have been measured experimentally.[25–27]But the elastic constants of TNTs have not been measured nor calculated yet.
In this paper,the single-cycle sheet of TiO2anatase(101)is curled into a single wall nanotube structure along different chiral directions. The elastic constants of the nanotubes are calculated by the Matsui and Akaogi(MA)potential function through using molecular dynamics.In order to verify the calculated results,we first use this potential function to calculate the elastic constants of bulk anatase and rutile,which demonstrate good accuracy.Then,the elastic constants of the titanium dioxide nanotubes with different chiral angles are further calculated,including Young’s modulus,shear modulus,and Poisson ratio.Such a prediction of the TNT elastic properties can provide good theoretical guidance for both experimental and practical applications.
2.Simulation methods
2.1.Building models
The nanotube symmetry and structure are described on the basis of the so-called layer folding.[28]The single-wall anatase TNT named(n,m)with open ends can be obtained by simple rotation of the(101)anatase surface along different crystalline orientations(Figs.1(a)and 1(b))and characterized by a chiral vector R,the expression of which is

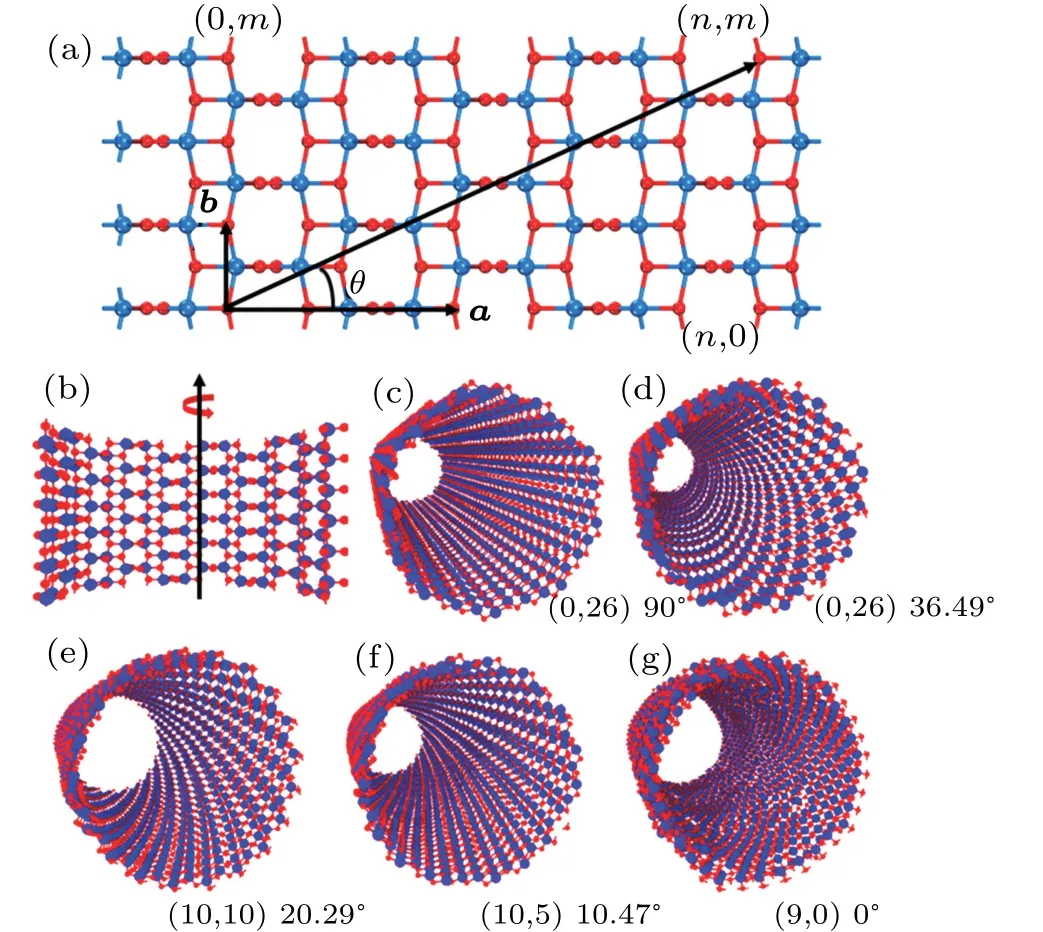
Fig.1.(a)Anatase(101)lattice and(b)rolling-up direction and process of nanotubes,with a and b denoting primitive translation vectors,and θ referring to chiral angle.(c)–(g)Different chiral structures of anatase(101)nanotubes.Solid red circle denotes oxygen atom and solid blue circle represents titanium atom.Radius of each nanotube is about 15 nm.
In Eq.(1),a and b are the primitive translation vectors of the two-periodic(2D)lattice in the layer.The chirality(n,m)is obtained by folding the layer in a way that the chiral vector becomes the circumference of the cross section of the nanotubes,[29]where n and m must be integers.The angle θ betweenandis called chiral angle,and the range of θ is generally in a range of 0◦–90◦,and θ is determined by the following equation:
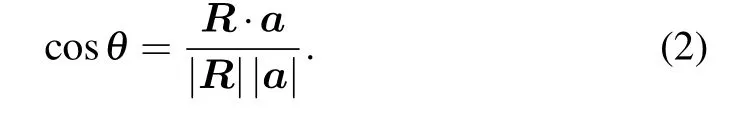
Here we select five different chiral anatase TNTs.The ratios of n to m of the nanotubes are 0(90◦),0.5(36.49◦),1(20.29◦),2(10.47◦),and ∞(0◦)(Figs.1(c)–1(g)),respectively.And the radius of nanotubes is nearly 15 nm.
2.2.Potential functions
Here we use the well-known MD(Molecular Dynamics)software package large-scale atomic/molecular massively parallel simulator(LAMMPS)to perform the calculation.[30]In this calculation,a classical potential function in the form of a pair of potential expressions with clear physical meaning is selected,which is an MA potential function.[31,32]The MA potential function is expressed as
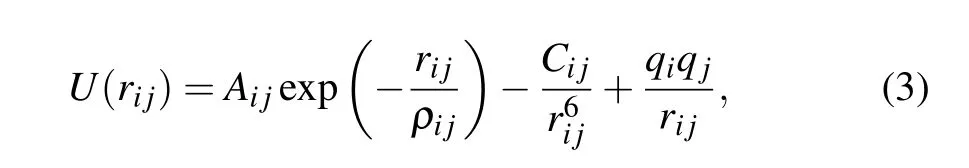
where U(rij)is the interaction potential between atoms,and rijis the distance between atom i and atom j. The charge of Ti and O atom are+2.196e and −1.098e,respectively and more potential function parameters are listed in Table 1. A Langevin thermostat is used for the temperature control with NVE ensemble.[33]Long-range electrostatic interactions are calculated by a particle mesh Ewald summation method.[34]The Newton’s equations of motion are integrated by Verletleapfrog algorithm. The cutoff radius is 10and periodic boundary condition is utilized in all three dimensions. The time step used in the simulation is 0.001 ps.

Table 1.Key parameters of MA potential function.
2.3.Calculation of elastic modulus
Bulk anatase,rutile,and TNTs are made of transversely isotropic materials,so they have a high degree of symmetry in their elastic properties. Based on Hooke’s law for elastic materials and using Voigt notation,the engineering moduli Cijcan be calculated from the following formula:
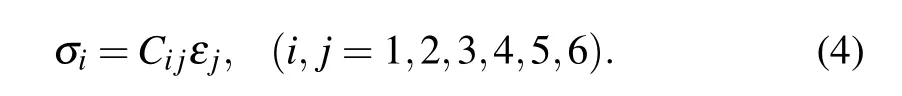
Both stress σiand strain εjare second rank tensors.In Voigt notation,[35]engineering moduli Cijcan be represented by a 6×6 symmetric matrix as[36]

For transversely isotropic materials:C11=C22,C23=C31,C44=C55,and C66=(C11−C12)/2,the engineering compliances Sijare also defined in the isotropic direction along the axis,similarly,in Voigt notation:

with S11=S22,S23=S31,S44=S55,and S66=2(S11−S12).The relationship between engineering moduli Cijand engineering compliances Sijis as follows:

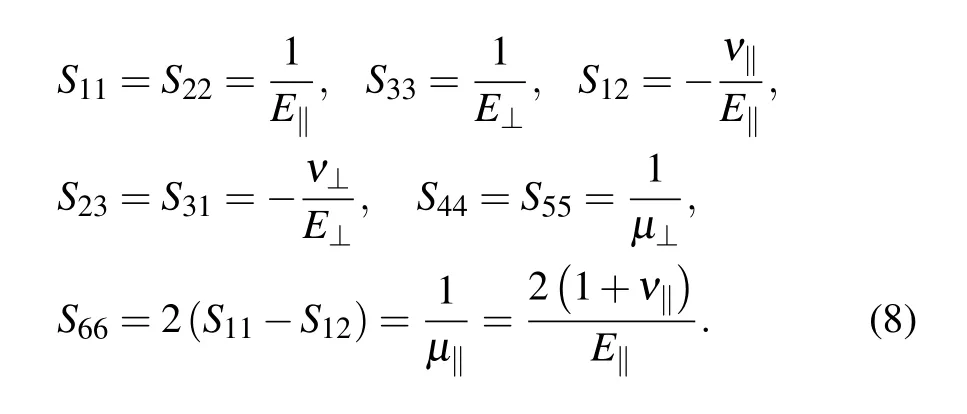
3.Results and discussion
Rutile is relatively stable in nature and the elastic constants of rutile are obtained experimentally.We use the MA potential function to calculate the elastic constants of bulk rutile from room temperature to 1000 K,and a fairly good agreement is found between our computed elastic constants and those from the experiments.[25,26](See Table A1 in Appendix A for more details). It is worth pointing out that the elastic constants gradually reduce as the temperature increases.The calculated value of C11is larger than the experimental value,and the rest of the elastic constants are in good agreement with the experimental values,which shows that the MA potential function can effectively predict the elastic properties of rutile TiO2.
However,the experimental values of anatase elastic constants have not been effectively measured.There exists only the bulk modulus for reference.[38]The elastic constants of anatase at 0 K can be accurately calculated by VASP,and the values are C11=395.2,C12=153.9,C13=156.0,C33=195.9,C44=47.3,C66=59.5(LDA/UPP);C11=336.5,C12=138.6,C13=136.0,C33=192.1,C44=49.4,C66=58.3(GGA/UPP);C11=320,C12=151,C13=143,C33=190,C44=54,C66=60.[23,24]The elastic constants calculated by LAMMPS with MA potential function are C11=419.3,C12=110.5,C13=105.6,C33=202.1,C44=52.5,and C66=50.4.And the calculation results of LAMMPS are in good agreement with those of VASP.Many properties of titanium dioxide have been investigated successfully by using the MA potential function.[39–41]Therefore,the MA potential function can also predict the elastic constants of anatase and nanotubes.
Figures 2(a)–2(e)show that neither of the elastic constants is significantly affected by temperature for each chiral anatase(101)nanotube. Therefore,temperature will not be an impact factor in the change of Young’s modulus nor Poisson ratio nor shear modulus.Hence,the following calculation results are all obtained at 300 K.
As can be seen from Table 2,the elastic constants of anatase(101)nanotubes are calculated to be smaller than those of anatase and rutile,and the difference in chiral angle will make the elastic constants of nanotubes different under the condition of the same radius.For the same chiral angle,the elastic constants C11and C33are larger than other elastic constants because of the transversely isotropic structures for nanotubes,which have a stronger load capacity on the Z-axis direction than on the other directions. For the different chiral angles that generally range from 0◦to 90◦,when the chiral angle of TNT is 0◦,its elastic constants are basically the minimum,which is the same as Young’s modulus and shear modulus. When the chiral angle of titanium dioxide nanotubes is 90◦,the elastic constants are the biggest in all elastic constants,which case is the same as those for Young’s modulus,shear modulus,and Poisson ratio.The Young’s modulus,Poisson ratio,and shear modulus of the nanotubes can be obtained from Eqs.(7)and(8),and Young’s modulus is determined by C11,C12,C13,and C33.But C11and C33are much larger than other elastic constants,so Young’s modulus of the nanotubes is mainly affected by C11and C33. Poisson ratio is affected not only by the elastic constant but also by Young’s modulus.Shear modulus is determined by Young’s modulus and Poisson ratio.By comparing the nanotubes(9,3),(9,6)as shown in the Supplementary information(Tables A2,A3 in Appendix A)with those in Table 2,it is found that when the radius of the nanotubes is nearly 15 nm,Young’s modulus does not change linearly with the increase of the chiral angle.However,when the chiral angle is 0◦,Young’s modulus,Poisson ratio,and shear modulus of the nanotubes are lowest.So the nanotubes with a certain chiral angle will improve the mechanical properties of nanotubes.
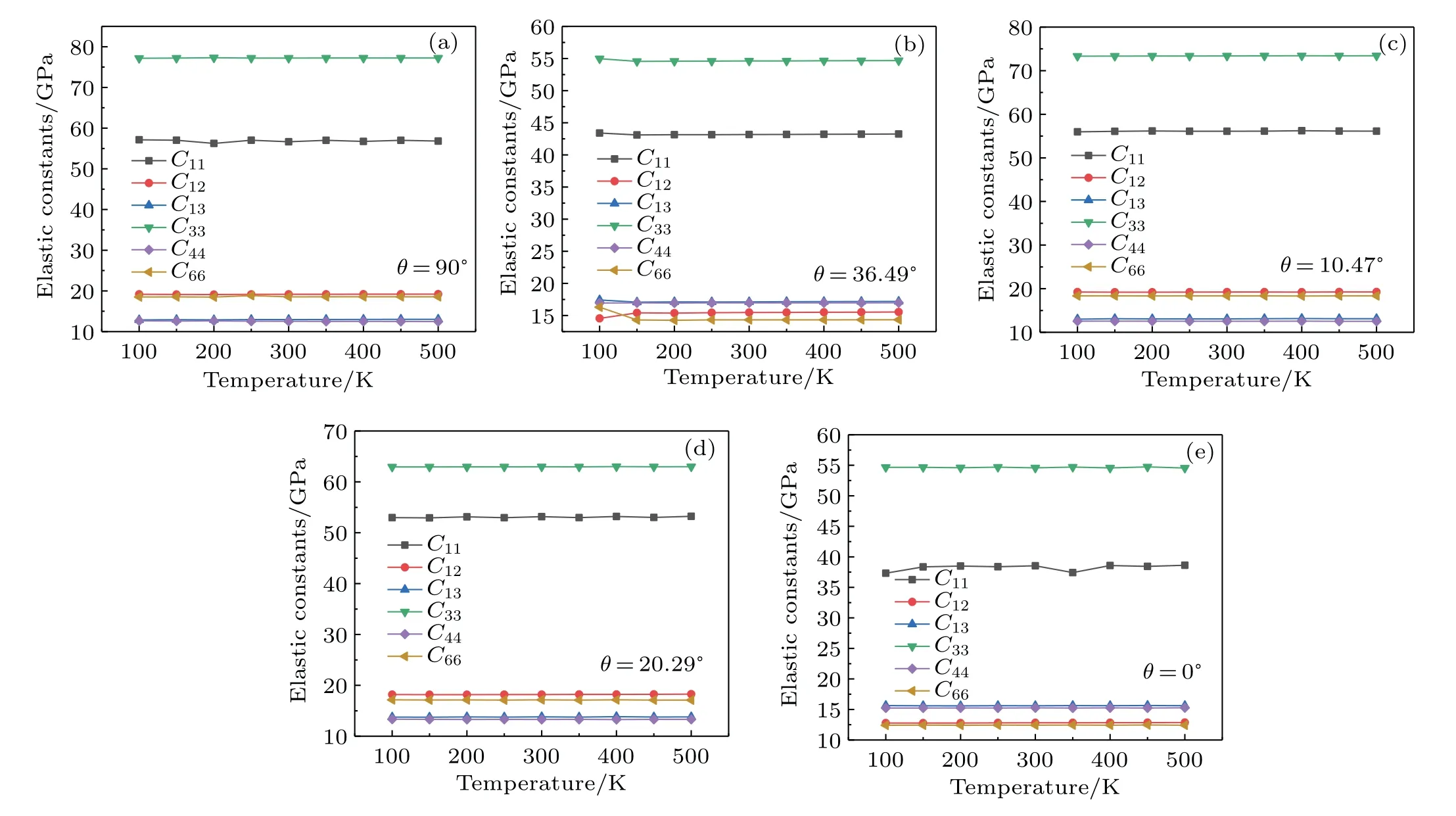
Fig.2.Elastic constants C11,C12,C13,C33,C44,and C66 at temperatures ranging from 100 to 500 K with chiral angles of(a)90◦,(b)36.49◦,(c)10.47◦,(d)20.29◦,(e)0◦,respectively.

Table 2.Elastic constants,Young’s moduli,Poisson ratios,and shear moduli(in unit GPa)of anatase(101)nanotubes with different chiral angles at 300 K,and radius of each nanotube of about 15 nm.
The elastic constants are also sensitive to the radius of the nanotubes.The relationship between the elastic constants and the radius of nanotubes under the same chiral angle is calculated,where the chiral angles are 7.03◦(Table A2),10.47◦(Table 3),13.85◦(Table A3),36.49◦(Table A4)respectively.
Table 3 displays that as the radius of each chiral nanotube increases,the elastic constants first increase and then gradually decrease.And C11and C33are most obvious because of the transversely isotropic structure.The four kinds of nanotubes with different chirality described above have an optimal radius range from about 10 nm to 15 nm.This means that the anatase(101)nanotubes should have maximum elastic constants in a radius range of about 10 nm–15 nm no matter what kind of chirality they have.

Table 3.Elastic constants,Young’s moduli,Poisson ratios,and shear moduli(in unit GPa)of anatase(101)nanotubes with different radii at chiral angle 10.47◦and temperature 300 K.
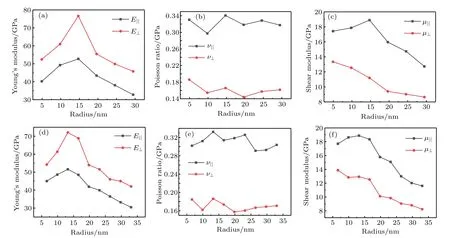
Fig.3.Plots of radius-dependent(a)Young’s modulus,(b)Poisson ratio,and(c)shear modulus(in unit GPa)of anatase(101)nanotubes with chiral angle 7.03◦and different radii.(d)Young’s modulus,(e)Poisson ratio,and(f)shear modulus(in unit GPa)of anatase(101)nanotubes with chiral angle 10.47◦and different radii.
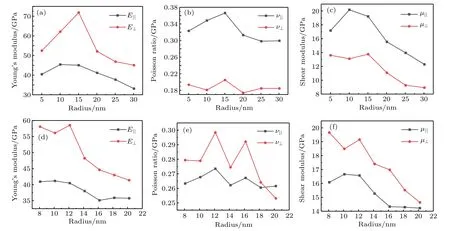
Fig.4.Plots of radius-dependent(a)Young’s modulus,(b)Poisson ratio,(c)shear modulus(in unit GPa)of anatase(101)nanotubes with chiral angle 13.85◦and different radii;(d)Young’s modulus,(e)Poisson ratio,and(f)shear modulus(in unit GPa)of anatase(101)nanotubes with chiral angle 36.49◦and different radii.
Because Young’s modulus is mainly determined by C11and C33,Young’s modulus also presents an increase and then decrease trend as radius increases.From Figs.3 and 4,it can follow that shear modulus and Young’s modulus have maximum values in a range of 10 nm–15 nm.The variation trends of Young’s modulus in an isotropic planeand Young’s modulus perpendicular to the isotropic plane E⊥are basically the same,so areandµ⊥.However,Poisson ratio fluctuates in a certain range.The calculated elastic modulus values are very similar to Young’s modulus values obtained from the direct compressive measurements of individual TiO2nanotubes[42](23 GPa–44 GPa)and nanoindentation[43](36 GPa–43 GPa)in a diameter range of about 35 nm–70 nm.From the analysis above,it can be concluded that in a nanotube radius range of 10 nm–15 nm,Young’s modulus and shear modulus will have maximum values.Saeed et al.[19]successfully improved the mechanical properties of epoxy resin by using nanotubes with a diameter range of 10 nm–20 nm.Because the chiral distribution of nanotubes used experimentally is so wide that it is difficult to determine a single chiral angle of the nanotubes,and thus there will be a lot of nanotubes with different chiral angles in the experiment.However,figures 3 and 4 show that among all the nanotubes,those in a radius range below 15 nm dominate their optimal mechanical properties.And for chiral nanotubes at 36.49◦in a radius range of 8 nm–14 nm,Young’s modulus does not differ from each other very much.Therefore,making the diameter of nanotubes as small as possible can improve the mechanical properties of composites.
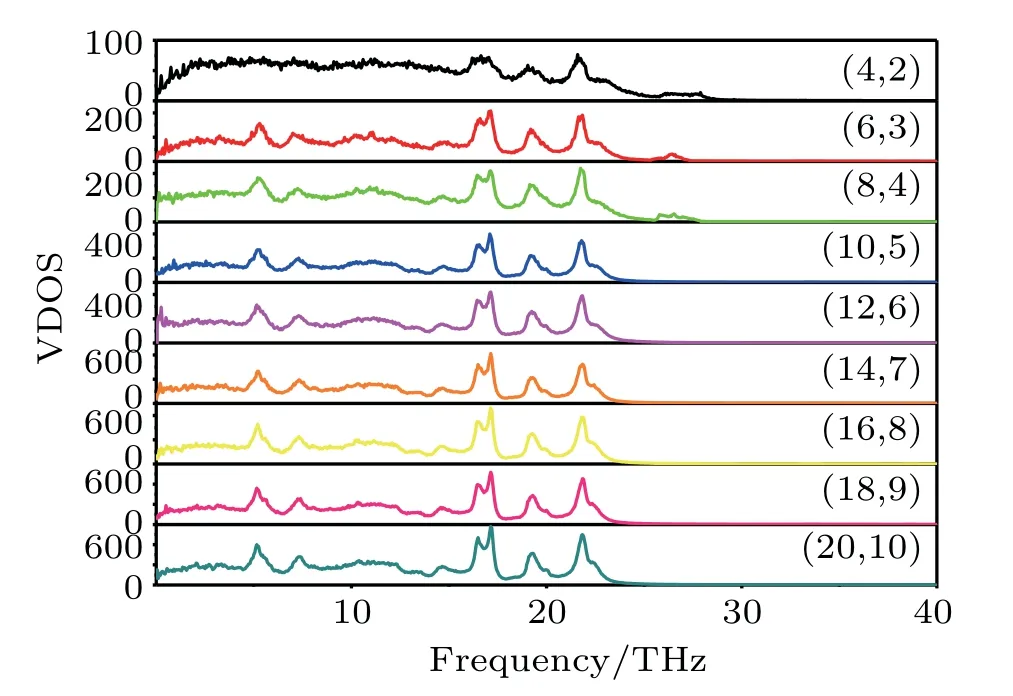
Fig.5.Plots of phonon density of states(DOS)versus frequency with chiral angle of 10.47◦and different radii from(4,2)to(20,10).
As shown in Fig.5,phonon densities of states of TNTs with different radii are calculated. Because atoms continuously vibrate at the equilibrium position,there is an interaction between atoms in the crystal,and the vibrations of each atom are not isolated from but interconnected with each other,thus forming elastic waves of various modes.The elastic properties of the crystal can be further analysed from the frequency of crystal vibration.It is worth noting that the nanotubes(4,2),(6,3),(8,4)have additional vibration modes at high frequencies ranging from 25 THz to 28 THz,which means that there is a strong elastic force between atoms.With the increase of radius,the high frequency vibration disappears,which shows that the large nanotubes do not have high frequency vibration and have low elastic forces compared with the small nanotubes.Therefore,elastic properties of nanotubes with small radius are better than those with large radius.This confirms those observations in Figs.3 and 4. The variation of calculated Young’s modulus and shear modulus are small when the radius of nanotubes is small(5 nm–15 nm)due to the high vibration frequency.However,as the radius increases,the elastic constant sharply decreases.
4.Conclusion and perspectives
In this work,the elastic constants,Young’s modulus,Poisson ratio,and shear modulus of anatase nanotubes were calculated by using MA potential function and transversely isotropic structure model.The elastic constants of TNTs are found to be not significantly affected by temperature.By calculating the elastic constants of nanotubes with the same radius but different chirality,it can be found that the elastic constants are not proportional to the chiral angle.In addition,both C11andC33are larger than the other elastic constants due to the transversely isotropic structure.By calculating the elastic constants of nanotubes with the same chirality but different radii,the elastic constants,Young’s modulus and shear modulus first increase and then decrease as radius increases.The maximum values appear in a radius range of 10 nm–15 nm,and Poisson ratio fluctuates in a certain range. Nanotubes with a radius range of 5 nm–15 nm have high frequency vibration and large elastic constants compared with big nanotubes.Therefore,the radius of the nanotubes should be as small as possible to enhance their mechanical properties in practice.
Acknowledgment
The author would like to thank Dr.Caizhuang Wang at Ames Laboratory for useful guidance and discussion during the molecular dynamics study.
Appendix A:Supplementary information
The following are the supplementary data to this article:Elastic constants Cij(in unit GPa)of rutile TiO2from 300 K to 1000 K;Elastic constants,Young’s modulus,Poisson ratio,and shear modulus(in unit GPa)of anatase(101)nanotubes with different radii at different chiral angles(7.03◦,13.85◦,and 36.49◦)at 300 K.

Table A1.Calculated and experimental results of elastic constants Cij(in unit GPa)for rutile TiO2 from 300 K to 1000 K.
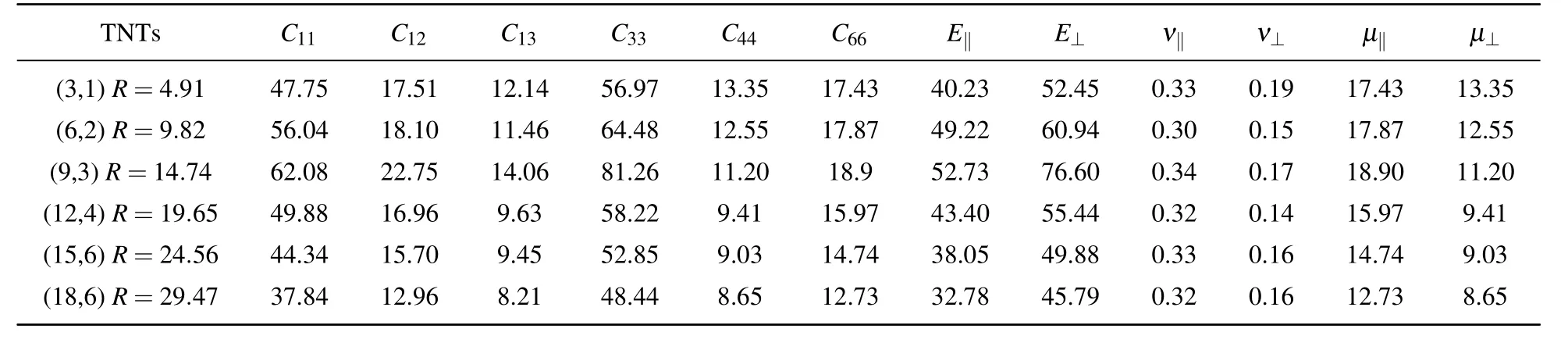
Table A2.Elastic constants,Young’s moduli,Poisson ratios,and shear moduli(in unit GPa)of anatase(101)nanotubes with different radii at chiral angle 7.03◦at 300 K.

Table A3.Elastic constants,Young’s moduli,Poisson ratios,and shear moduli(in unit GPa)of anatase(101)nanotubes with different radii at chiral angle 13.85◦at 300 K.
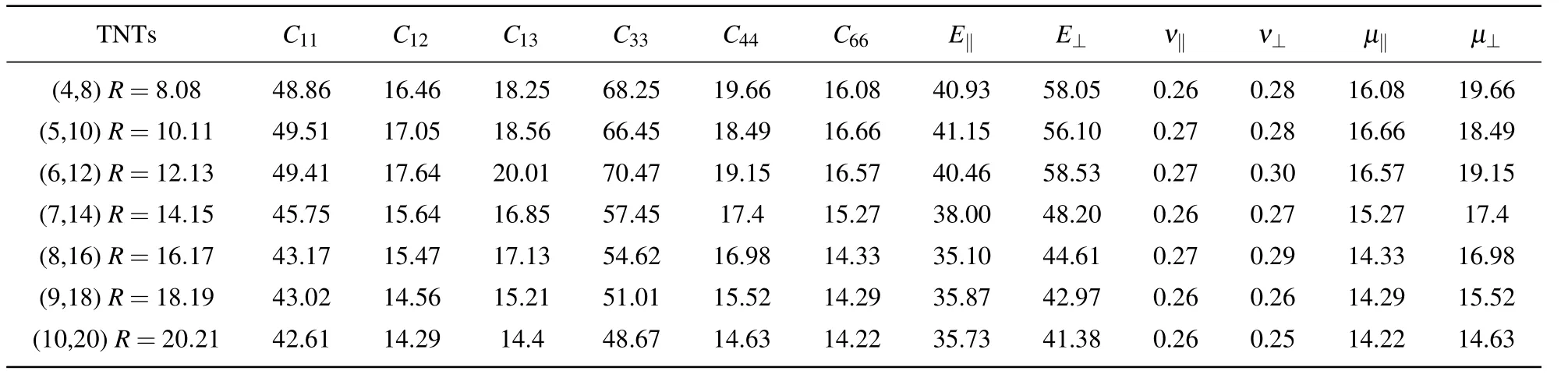
Table A4.Elastic constants,Young’s moduli,Poisson ratio,and shear moduli(in unit GPa)of anatase(101)nanotubes with different radii at chiral angle 36.49◦at 300 K.
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- Theoretical analyses of stock correlations affected by subprime crisis and total assets:Network properties and corresponding physical mechanisms∗
- Influence of matrigel on the shape and dynamics of cancer cells
- Benefit community promotes evolution of cooperation in prisoners’dilemma game∗
- Theory and method of dual-energy x-ray grating phase-contrast imaging∗
- Quantitative heterogeneity and subgroup classification based on motility of breast cancer cells∗
- Designing of spin filter devices based on zigzag zinc oxide nanoribbon modified by edge defect∗
