Enhanced spin-dependent thermopower in a double-quantum-dot sandwiched between two-dimensional electron gases∗

Feng Chi(迟锋), Zhen-Guo Fu(付振国), Liming Liu(刘黎明), and Ping Zhang(张平)

1School of Electronic and Information Engineering,University of Electronic Science and Technology of China,Zhongshan Institute,Zhongshan 528400,China

2Institute of Applied Physics and Computational Mathematics,Beijing 100088,China

Keywords:quantum dot,spin-dependent thermopower,two-dimensional electron gases

1.Introduction

In recent years,the spin caloritronics[1]has attracted much attention due to the attractive applications in spintronic devices driven by thermal gradients. It is a subject devoted to the generation and manipulation of 100%spin-polarized and pure spin currents denoted by the corresponding thermopower in spin-dependent thermoelectric effect. This research topic received rapid development ever since the breakthrough experiment carried by Uchida et al.,who measured the spin-Seebeck effect(SSE)inducing a spin bias or pure spin current as a result of a temperature difference between the edges of a ferromagnetic Ni81Fe19film.[2]From then on, the SSE has been extensively investigated both theoretically and experimentally in various materials,including ferromagnetic insulators,[3,4]ferromagnetic metals,[5]ferromagnetic semiconductors,[6]nonmagnetic materials,[7]paramagnetic materials,[8]antiferromagnetic materials,[9]metal–ferromagnet insulator interface,[10]and topological insulators.[11–14]It has been proved that besides the applications in spintronics,devices based on SSE are also promising in heat-to-electricity conversion and precise detection of small temperature difference because of the weak spin–spin interactions.[1,2]

Until now,one of the bottlenecks of SSE is that the magnitude of the 100%spin-polarized and pure spin thermopower is still so small that may be overwhelmed by the charge one.In view of this,recent efforts have been devoted to nanoscale materials,such as superlattices,[15]nanotubes,[16]silicon nanowires,[17,18]and single-molecular junctions.[19–21]In such materials, the electron density of states forms a peak configuration that enhances the thermopower and the thermoelectric efficiency. Furthermore,the thermoelectric effect will become more obvious with decreasing system’s dimensions.[22]As the lowest-dimensional system,quantum dots(QDs)[23,24]in which the electrons are confined in all the three directions then have been extensively studied.The magnitude of the thermopower is significantly enhanced in QDsbased structures mainly due to the quantization of the energy levels and the quantum interference effects.[25–42]The latter occurs in multi-path configurations,which induce Aharonov–Bohm effect,[25,26,33,34,43]Fano effect,[33,37]as well as Dicke effect.[39,40,42]Especially,the thermopower has a zero point around the antiresonant states,at each side of which there is a sharp peak.In the presence of the magnetic field,the positions of the peaks in the spin-up and spin-down thermopowers are shift to opposite directions in energy space due to the Zeeman splitting in the dots.If the energy state of the positive peak in the thermopower of one spin component overlaps with that of the negative one of the opposite spin component,the charge thermopower may be zero but the pure spin one is finite.This is likely to occur when the Zeeman splitting is weak. For a strong magnetic field,the peaks of the spin-up and spin-down thermopowers are fully separated in dot level space,inducing a large 100%spin-polarized thermopower,i.e.,only one spin component electrons are accumulated on the two terminals of the structure.In the closed circuit,only one certain spin direction electrons flow through the system,i.e.,the spin-filter effect.

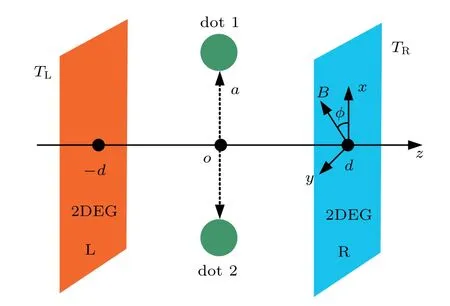
Fig.1.Schematic plot of the double quantum dots coupled to the left and right 2DEGs held at different temperatures.

In the above mentioned systems, the QDs are coupled to the external metallic,[25–27]ferromagnetic,[37]or superconductor[42]leads.Experimentally,QDs are mainly defined either self-assembly or electrically in two-dimensional gases(2DEGs).[44–46]Here we investigate the SSE in a system composing of double QDs(DQD)embedded between the left and right 2DEGs which are prepared in doped quantum wells[44,45]held at different temperatures as shown in Fig.1.It is known that 2DEG has successfully realized between heterojunctions.It is the cornerstone for other nano-scale devices,such as quantum wells,quantum wires,and quantum dots.As compared to other conventional electrodes coupled to the quantum dots,there are at least two advantages:(i)2DEGs are easily prepared and integrated with the quantum dots.In fact,in many cases,the quantum dots are directly defined from the 2DEGs;(ii)electron tunneling through such a system strongly depends on the energy states in the 2DEGs,which has seldom been studied in previous works.It has been demonstrated that the energy-dependent tunneling will drastically influence the thermoelectric effect,which is also the motivation of the present work.In the absence of the magnetic field,the coherence between the DQD is controlled by the coupling through the continuum of electronic states in the 2DEGs.If the separation between the two dots a is comparable to the electron Fermi wavelength in the 2DEGs,the electron transmission depends on the system eigenstates rather than on the individual QDs,leading to the Dicke effect characterized by sharp asymmetric line-shape in the conductance that enhances the magnitude of the thermopower.The in-plane magnetic field will induce splitting of the energy state in both the 2DEGs(hereafter is called as Zeeman energy)and the QDs(Zeeman splitting).In this paper,we consider that the distance between the DQD is smaller than the Fermi wavelength in the 2DEGs to focus on the Dicke tunneling regime.

2.Model and method

The system Hamiltonian is written asHDQD+HT,where Hα(α=L,R)is the 2DEG Hamiltonian in the α-th plane,HDQDis the Hamiltonian of localized states in the dots,and HTdescribes the tunneling between them.The 2DEG Hamiltonian has the form

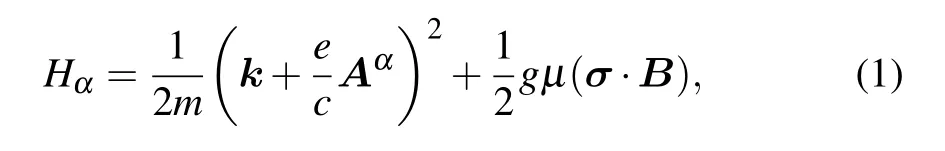
where the in-plane magnetic field=B(cosφ,sinφ,0)with φ the angle formed between the magnetic field and the x axis.The momentum is=(kx,ky,0),andin whichis the Pauli matrix.The 2DEGs are assumed to individually locate at=(0,0,zα)withFor the static magnetic field,the vector potential isFrom the Schrödinger equation,the electron’s eigen-energy for identical left and right 2DEGs is obtained asεkσ=k2/2m+σωzwith ωz=gµBB/2 the Zeeman energy.The constants g andµBare the Landé factor and Bohr magneton,respectively.The spin index σ=±1 corresponds to the spin-up(down)direction.If we choose the spin quantization axis to be along the z direction,σ also indicates the chirality of the 2DEGs.The corresponding eigen-function is calculated according to the standard technique

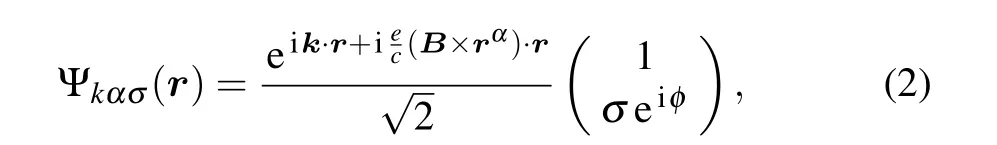
where c and e are the light velocity and electron charge,respectively. The Hamilton of the 2DEGs can be written in the second quantization formwhereis the electron’s creation(annihilation)operator.

In Eq.(1),the Hamiltonian describing the DQD is given bywhereis the electron’s creation(annihilation)operator in dot-j having energy leveland ε1(2)=εd+(−)∆with ∆and Ezbeing the level detuning between the two dots and the Zeeman splitting in them,respectively.Here we use s=±1 to indicate the spin up and down electrons in the DQD.The Hamiltonian HTfor tunneling between the 2DEGs and the DQD is given byThe quantityis the electron transition matrix element between dot stateand 2DEG statewhich is related to the wave-function in the 2DEGs bywhere tαis the tunneling amplitude between the dots and 2DEGs and rjis the in-plane projection of the coordinate of dot-j.The electron transmission coefficient can be calculated with the help of the lattice Green’s function method as[33]

where the retarded Green’s functionis a 4×4 matrix in the configuration and spin space,and is given by

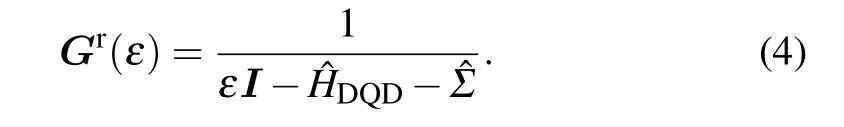
Here the diagonal matrix of the dots isThe advanced Green’s function isThe 4×4 matrixis the self-energy due to coupling between the dots and 2DEGs. Its matrix elements in spin and configuration space are given by[45]

Recalling the relationship betweenand the eigenfunction in the 2DEGs,the explicit form of the self-energyis

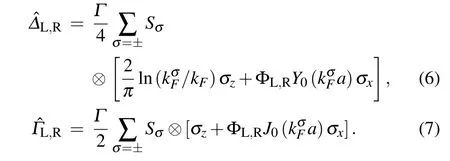
Here we have assumed that the tunneling strengths between the dots and the two 2DEGs are equal to each other(tL=tR),and setThe matrixis in the dot spin space,and σx,zis the Pauli spin matrix. The spin-dependent Fermi wave vector iswhere EFis the Fermi energy in the 2DEGs andY0(x)and J0(x)are the Bessel functions of the first and second kinds,respectively.In Eq.(6),is the Aharonov–Bohm factor.

In the linear response regime,i.e.,under infinitely small potential difference ∆V and a temperature difference ∆T between the left and right 2DEGs,the conductance Gσand thermopower Sσare given with the help of coefficients Kn,σ(n=0,1,2)defined as[28–34]

where Tσ(ε)is the spin-resolved transmission coefficient,and f(ε,µ)=1/{1+exp[(ε −µ)/kBT]}is the Fermi distribution function with Boltzmann constant kB,system equilibrium temperature T,chemical potentialµin the 2DEGs.The interested quantities are then given in terms of Kn,σas Gσ=eK0,σand Sσ=−K1,σ/(eTK0,σ). Furthermore,the charge(spin)thermopower is defined as

3.Numerical results

In the following,we give our numerical results assuming identical left and right 2DEGs with the same Zeeman energy ωz.The dots’level is set to be εd=0.Figure 2 shows the spinresolved conductance and thermopower as functions of the chemical potentialµfor different values of the dot level detuning ∆.Here we choose a small akF=0.1Γ,which means that the two dots are near to each other and will result in obvious interference effect.For identical dots level ∆=ε1−ε2=0,the conductance in Figs.2(a)and 2(c)shows a double-peak configuration with different peaks’width,which is a characteristic signature of coherent Dicke effect arisen from quantum interference when electrons tunneling through different channels(the black solid lines).[38,39]In fact,under this condition,the spin-dependent conductance in the presence of QD Zeeman energy Ezcan be explicitly written as

with

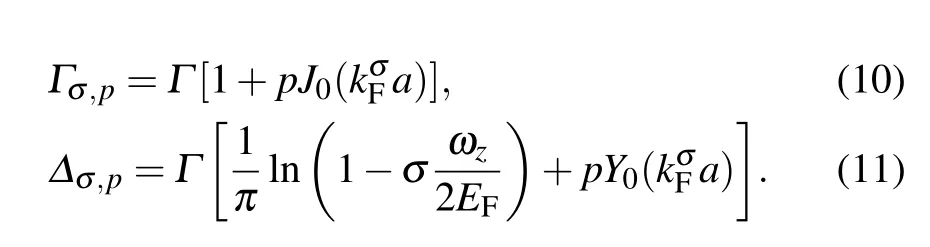
The above equations indicate that the conductance is composed of a broad Breit–Wigner peak with width Γσ,+and a narrow one with width Γσ,−. The corresponding positions of the two peaks are individually centered aroundµ−EF=±(−εd−σEz/2 −∆σ,±).Turning on the level detuning between the two dots(),the interference effect becomes more pronounced and the narrow peak atµ>0 becomes asymmetric changing from a dip(antiresonance)to a broader peak(resonance). This is because for finite ∆,the two dots having different energy levels ε j now couple to the 2DEGs’states with different Fermi momenta,which results in either destructive or constructive interference effects.With increasing ∆,the dip in the low-energy regime induced by the destructive interference becomes more obvious.[38,39]In addition,the peaks in the spin-up and spin-down conductances are shift to oppositive directions in the energy space by the Zeeman energy Ezin the DQD.

Figures 2(b)and 2(d)indicate that the thermopower around the broad Breit–Wigner peak in the conductance is neglecting small,but develops sharp peaks around the position of the antiresonance in the conductance. The reason is that the thermopower Sσis proportional to the ratio of K1,σ/K0,σ,and the conductance Gσ=eK0,σis suppressed at the antiresonance energy. In bulk materials,the reduction of the electrical conductance is always accompanied by the reduction of the thermal conductance due to the Wiedemann–Franz law,[28]and then the magnitudes of the thermopower and the thermoelectric efficiency can hardly be changed. In quantum size devices,however,the Wiedemann–Franz law may be violated by the quantum interference effect[30,31,33]in multi-path systems,leading to the enhancement of the thermoelectric efficiency and the thermopower.In addition,when the chemical potentialµis above(below)the antiresonance energy,the thermopower is negative(positive)because the majority carriers are holes(electrons),and the value of Sσis peaked with opposite signs.Apart from the antiresonance energy,the magnitude of the thermopower is quite small despite of the existence of the resonance peaks in electrical conductance.[30,31,33,38]Since the peaks in the spin-up and spin-down themopowers are separated in energy space by the Zeeman splitting in the DQD,a nearly 100%spin-polarized thermopower is obtained in a large energy regime.

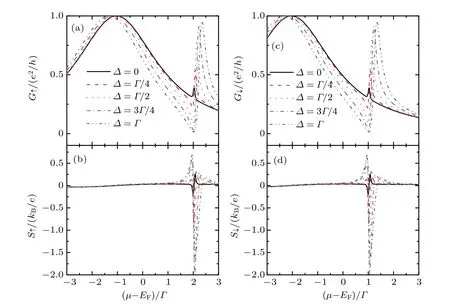
Fig.2.Spin-dependent conductance Gσ in(a)and(c),and thermopower Sσ in(b)and(d)as functions of the chemical potentialµfor different values of the dots’level detuning ∆.The other parameters are dots’separation akF=0.1Γ,dot’s level εd=0,temperature T=0.02Γ,Zeeman splitting Ez=0.5Γ,Zeeman energy ωz/EF=0,and magnetic flux φ=0.

In Fig.3,we examine the impacts of the dots’separation characterized by akFon the conductance and the thermopower with fixed Ez=0.5Γ.Since the magnitude of the thermopower around the broad Breit–Wigner peak in the conductance is quite weak,we only focus on the behaviors of the conductance and the thermopower near the Dicke regime.As shown in Figs.3(a)and 3(c),the position of the narrow Dicke peak in the conductance will be monotonously shifted to the higher energy regime by decreasing akF,with the reduction of the peak height.Moreover,the peak becomes sharper because the line-width function in Eq.(9)depends on the value of akF.The shift of the resonant state by the decrease of akFis attributed to the QDs’level repulsiondue to the coupling between the dots through the 2DEGs,while the narrowing of the peak originates from weaker coupling of the antisymmetric state to 2DEGs as the electron Fermi wavelength exceeds the separation a between the DQD.This is an unique result as compared to those in the previous works where the energy-dependence of the dots–leads coupling was neglected under wide-band approximation.[28,29]Particularly,the antiresonance in the conductance becomes more obvious with decreasing akF,i.e.,the conductance is further reduced.Consequently,the thermopower near the antiresonance state is enlarged as shown in Figs.3(b)and 3(d).The Zeeman splitting Ezin the dots shifts the sharp peaks in the spin-up and spin-down thermopowers to different energy states,inducing nearly 100%spin-polarized thermopower that is useful in the realization of spin-filter devices to separate the spin-up and spin-down electrons.

We study in Fig.4 the behaviors of the spin-dependent conductance Gσand thermopower Sσvarying with the temperature and magnetic flux penetrating through the structure,respectively. To focus on the peak evolution of Sσ,we set the chemical potentialµ=1.04Γ,where S↓develops a peak for Ez=0.5Γ.The property of S↑resembles that of S↓.Figure 4(a)indicates that G↓increases with increasing temperature in low temperature regime.With further increased temperature,it reaches a plateau and then keeps at a constant value(the dashed red line).[28]The change of the spin-up conductance G↑is very small as shown by the solid line.The absolute value of S↓in Fig.4(b)first is enhanced and then decreased by increasing temperature.At sufficiently high temperature,it will reach a small constant value.[28]Similar to the case of the conductance,the variation of Sσwith the temperature is quite weak as indicated by the solid line in Fig.4(b).The optimized temperature for the large value of S↓is about kBT=0.02Γ.At high temperature,the Dicke effect arising from the quantum interference effect will be destroyed by the electrons’thermal motion,resulting in weak themropower.Figures 4(c)and 4(d)show the behaviors of Gσand Sσas functions of the magnetic flux φ.Although the value of G↑strongly depends on the magnetic flux,that of S↑is almost unchanged. For the case of spin-down electrons,however,the conductance develops a dip for integer values of the magnetic flux φ=nπ,where n=0,1,2,....Correspondingly,the thermopwer S↓is peaked at this value of magnetic flux,resulting in a large spin polarization of the thermopower p=(S↑−S↓)/(S↑+S↓),which can be used for a spin filter.

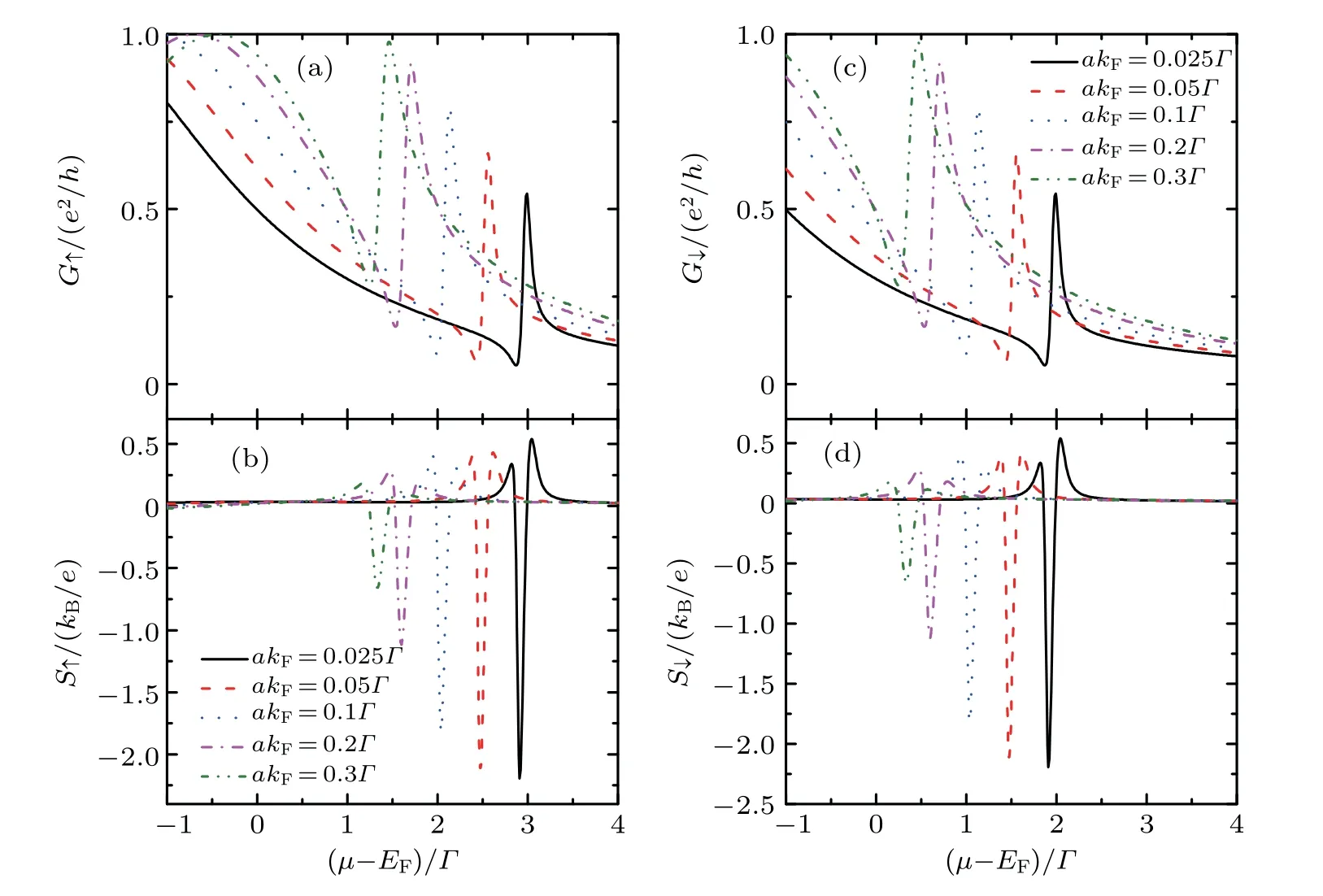
Fig.3.Spin-dependent conductance Gσ in(a)and(c),and thermopower Sσ in(b)and(d)as functions of the chemical potentialµfor different values of the dots’separation akF with fixed level detuning ∆=Γ/2.The other parameters are the same as those in Fig.2.

Besides the Zeeman splitting Ezin the dots and the magnetic flux φ,the magnetic field applied on the system also induces Zeeman energy in the 2DEGs denoted by ωz. Figures 5(a)and 5(c)show that the width of the sharp peak in the conductance is further narrowed by increasing ωz.This is induced by the tunnel coupling of the dots’levels to the electrons in the 2DEGs with different Fermi momenta,which changes the line-width function toas given by Eq.(9a). According to Eq.(9b),the peak position will also be changed by the Zeeman energy as ∆σ,−=With increasing magnetic feild,the spin-up(down)conductance develops a small dip at the left(right)side of the main peak.The Zeeman energy ωzhas less impact on the thermopower as shown in Figs.5(b)and 5(d),unless the new low peak induced by the newly developed dip in the conductance. It is noticed that the Zeeman energy in the 2DEGs has the same effect on the spin-up and spin-down electrons.This is because the properties of the conductance and the thermopower are the integration of the transmission function over the energy in the 2DEGs,and then the function of energy quantization in the 2DEGs disappears.

In the above discussions,the peaks’positions in the conductance and thermopower of different spin components are well separated by the Zeeman splitting in the dots,and then a nearly 100%spin-polarized current will be generated. In spintronics,another important current is the pure spin one,[47]which emerges when spin-up and spin-down currents with the same magnitude follow in the opposite directions. In open circuit,the pure spin current changes into a spin bias which is the pure spin thermopower Ssarisen from the thermoelectric effect.Recall that there are respectively one positive and one negative peaks at the two sides of each zero point in the thermopower Sσ,the pure spin thermopower can be realized when the position of the positive peak of one spin component overlaps with that of the negative peak of the other spin component.It requires that the separation between the spinup and spin-down dots’levels,realized with the help of the Zeeman splitting Ez,is quite small.In Figs.6(a)and 6(b),we set Ez=0.025Γ,and show that both S↑and S↓separated by Ezhave a zero point near the antiresonant states and develop two peaks with opposite values positioned at its two sides,respectively. As a result,the charge thermopower Sc=0 and the pure spin thermopower Sshas a finite value(see the dot).Apart from the antiresonant states,the pure spin thermopower without the accompany of the charge one can hardly emerge.It can also be seen that the maximum of|Ss|can be larger than that ofIn the case of Ez=0.05Γ,the distance between the peaks in S↑and S↓is enlarged and the absolute value of Ssis enhanced accordingly.

As illustrated in Figs.3 and 6,the Zeeman splitting in the dot will induce the position shift of the thermopower and result in 100%and pure spin thermopowers. Whereas,the Zeeman energy in the 2DEGs has little impact on the thermoelectric processes(see Fig.5). The conductance and the thermopower also exhibit Aharonov–Bohm oscillations as a function of the magnetic flux penetrating the whole structure.In summary,our results show that the Zeeman splitting in the DQDs is crucial for the polarization of the conductance and the thermopower,whose magnitude is sensitive to the properties of 2DEGs,DQDs,and the magnetic field.The Zeeman energy in the 2DEGs,however,has little impacts on the above two quantities.

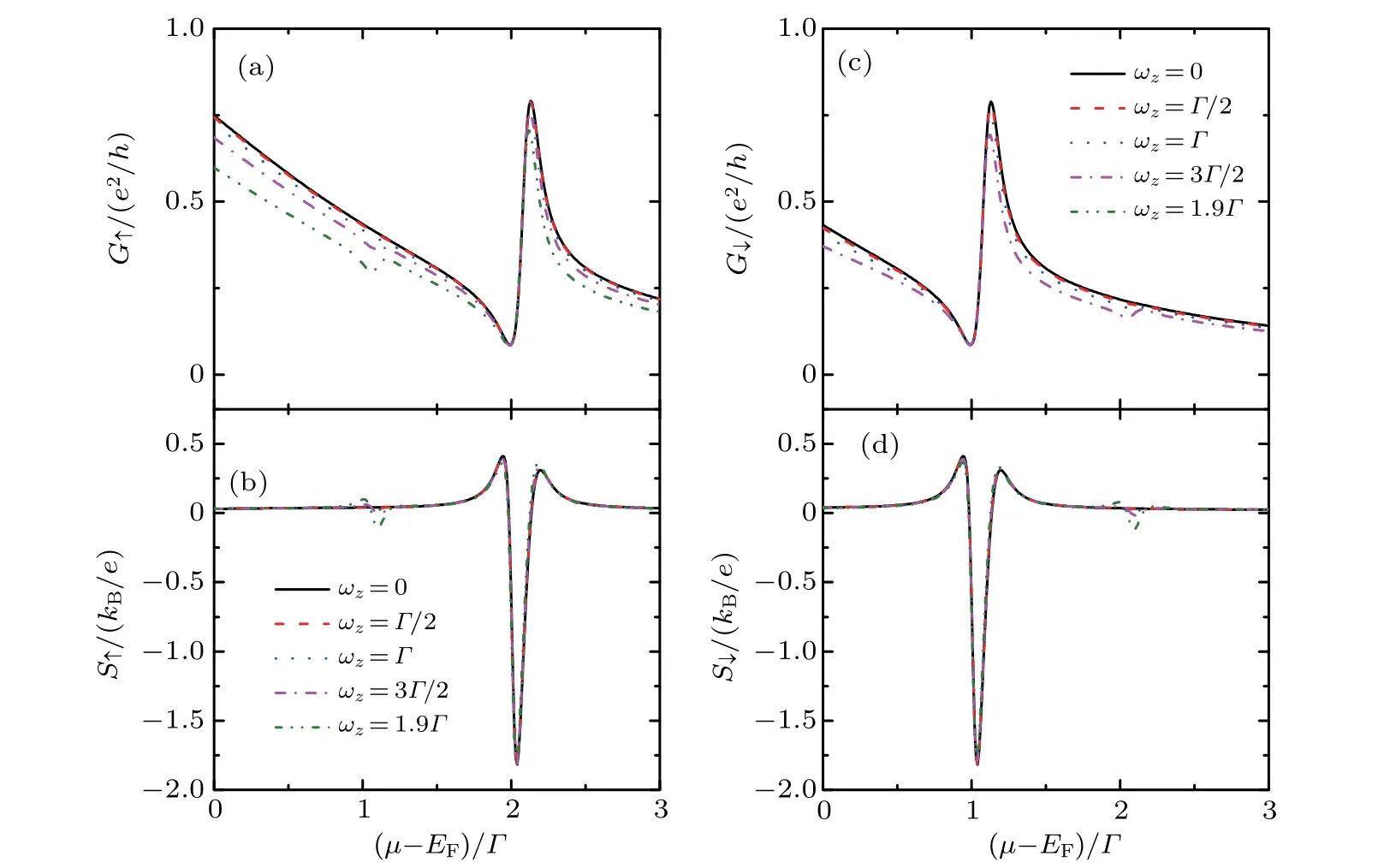
Fig.5.Spin-dependent conductance Gσ in(a)and(c),and thermopower Sσ in(b)and(d)as functions of the chemical potentialµfor different values of the Zeeman energy ωz/EF with fixed dots’level detuning ∆=Γ/2.The other parameters are the same as those in Fig.2.

Fig.6.Spin-dependent thermopower Sσ in(a)and(c),and charge and spin thermopowers in(b)and(d)as functions of the chemical potentialµat temperature T=0.015Γ/kB.In(a)and(b),∆=0.05Γ,Ez=0.025Γ,and in(c)and(d),∆=Ez=0.05Γ.The other parameters are the same as those in Fig.2.

4.Conclusion

We have investigated the thermospin effect in a DQD coupled to the left and right 2DEGs under an in-plane magnetic field,focusing on the generation of both 100%spinpolarized and pure spin thermopowers. The magnitude of the thermopower is remarkably enhanced around the antiresonant state due to the Dicke tunneling processes arisen from the interference effect in this multi-path structure.Under relatively large Zeeman splitting in the dots,a nearly 100%spinpolarized thermopower can be realized because the dots’levels are fully separated.Its magnitude can be efficiently adjusted by varying the properties of the 2DEGs,the DQD,and the magnetic field.For small Zeeman splitting,the peaks in the spin-up and spin-down thermopowers are near in energy space,and a pure spin thermopower may emerge when the peaks of different spin components with oppositive signs appear at the same energy state.Our results also show that the Zeeman energy in the 2DEGs has less impact on the spin polarization of the thermopower,since the energy quantization in the 2DEGs induced by the magnetic field is integrated out.