预给极点的二元向量连分式插值

孙思梦 赵前进

（安徽理工大学数学与大数据学院 安徽淮南 232001）

在工程实践和自然科学等研究领域中，我们经常会遇见有极点的奇异函数和大量的无规则的数据的计算问题。连分式有理插值无疑是为这些问题的近似解提供了有效的解决途径之一。前人在研究这方面做了巨大贡献[1-13]。文献[5]给出了二元对角向量有理插值，在主对角线和副对角线上进行二元向量值有理插值，分别给出了两种计算方法：一是直接计算二元对角向量值有理插值，二是通过Samelson逆计算的一种特殊的初等运算，构造出一种矩阵算法。文献[6]是给出的二元向量有理插值在矩形网格上充要条件的问题。即根据给定的数据解方程组，直接检验出相关插值的存在性，从而构造出对应的二元向量值有理插值的表达式，利用二元分支向量值连分式和二元向量值有理插值函数的Samelson逆，得出的表达式与传统的二元分支向量值连分式相比更直接。

一、向量的广义逆

设R2中的点集为Πm，n对应的d维向量集为

=(V*为V的共轭向量)

||为向量的模

则可验证出向量V→的Samelson逆向量所具有的性质：

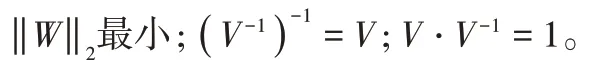
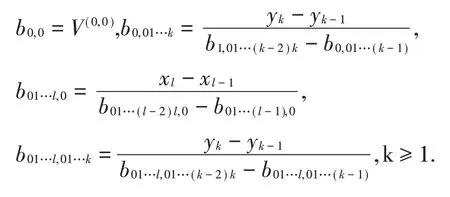
二、二元非张量积型连分式插值

二元有理插值是一元有理插值问题的扩展，同时它比一元有理插值的情形繁琐的多。而且二元多项式P(x，y)=pijxiyj的次数，可有两个不同的定义，一个是另一个是分别关于x和y定义次数。这样多项式的集合分别是Pk和Pm，n。在讨论插值问题时应该明白是在什么情况下的插值。

设f(x，y)为定义在平面有界区域D上的连续函数，{x0，x1，…}和{y0，y1…}为实数或复数点列，求二元有理分式函数其中N(x，y)∈Pn，M(x，y)∈Pm，使之满足插值条件0，1，…n1；j=0，1…n2)。

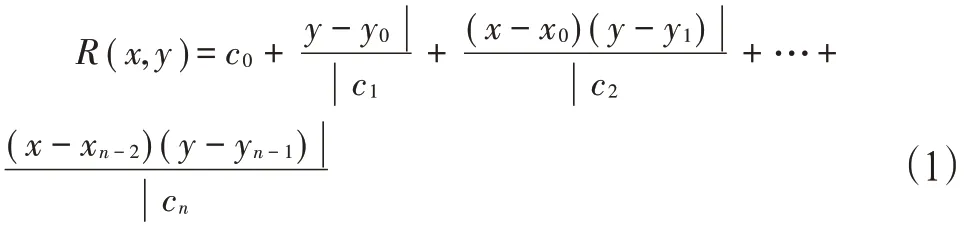
插值系数满足ci=φ0，…i=φ[x0，…，xi；y0，…，yi]，i=0，1…，n

其中系数算法如下：

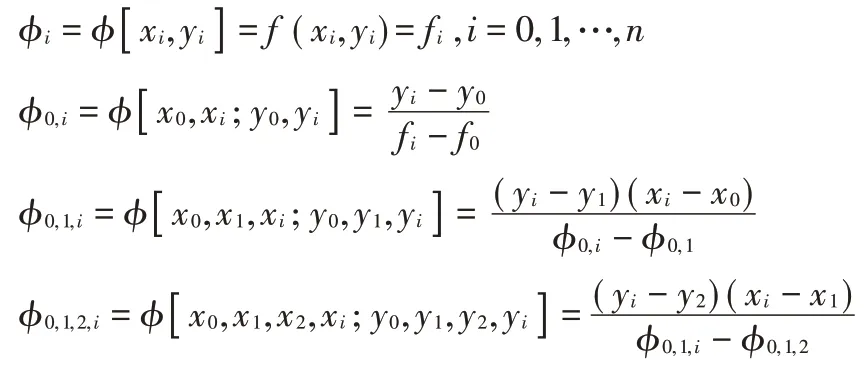
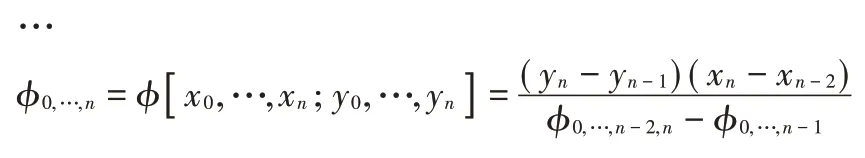
三、预给极点的二元向量连分式插值

设向量(x0，y0)，(x1，y1)，…，(xn，yn)是在区间[a，b]上的n+1个不同的插值节点，v(i)=v(xi，yi)，i=0，1，…，n是被插值向量函数v(x，y)在这些节点处对应的向量值。

Ω=是向量值函数v(x，y)的预给极点，v(x，y)预给的p(p=个极点用(aj，bj)(j=1，2，…，s)表示，重数记作kj(j=1，2，…，s)。根据Berrut提出的处理预给极点的重心有理插值方法[13]，如下：

进而得到预给极点的二元向量有理插值

四、数值例子

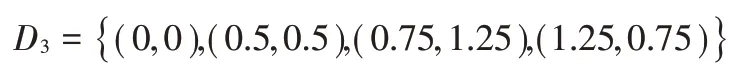
对应函数值分别为：

显然重数d(x，y)=(x-1)2+(y-1)2，则=d(xi，yi)f(xi，yi)，i=0，1，2，3

基于向量的Samelson逆，根据上文中的二元非张量积型连分式系数的算法算出系数：

得到二元非张量积型连分式插值函数为：

从而

利用文献[3]中陈欢欢提供的二元对角向量值有理插值计算方法，选取五个插值节点(x0，y0)=(0，0)，(x1，y1)=(0.5，0.5)，(x2，y2)=(0.75，1.25)，(x3，y3)=(1.25，0.75)，(x4，y4)=(1，1)其中f(x)在(1，1)处的向量值是无穷大。基于Samelson逆计算出满足插值条件的二元向量有理插值函数

两种插值方法分别在点(0.75，0.95)和 (0.85，0.95)处进行误差比较如表1所示。

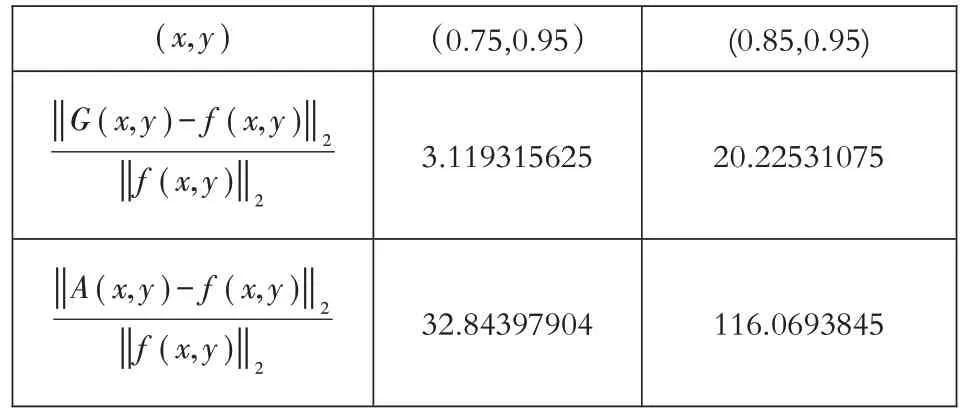
表1 两种插值方法的误差对比

由表1中的误差分析比较结果来看，本文中所给出的非张量积型插值函数方法构造出的插值显然在极点(x，y)=(1，1)然附近相对误差较小，而且极点的重数保持不变，说明了本文所给出方法的可行性。

五、结语

本文研究的是预给极点的二元连分式插值，方法是通过预给极点的位置和重数，将预给极点的向量值插值转化为无预给极点的向量值插值，然后基于Samelson逆分别构造出一个二元向量非张量积型插值函数和一个二元对角向量值有理插值，不仅有预给的极点，而且极点保持了原有的重数，并且通过数值例子，比较两类插值算法的相对误差，二元非张量积型插值函数的相对误差更小，说明了其算法的有效性。