基于组合模型的接地网腐蚀速率预测算法

黄欢　刘彦辰　高翔　彭敏放

摘   要：及时掌握并准确预测接地网的运行工况，从而对其进行预警和维护，是保证电力系统安全稳定运行的重要举措。针对接地网腐蚀数据的小样本与非线性特征，且目前单一预测模型存在预测精度不足的问题，提出了一种结合改进最小二乘支持向量机与误差校正的组合模型，将其应用于接地网腐蚀速率预测。该法采用遗传算法优化最小二乘支持向量机参数，为提高模型的预测精度，应用误差预测校正模型修正其预测结果，降低了极大误差出现的可能性，提高了预测模型的稳定性。结果表明，采用組合模型对接地网腐蚀速率进行预测，比采用最小二乘支持向量机模型具有更高的预测精度，更适用于接地网腐蚀速率的预测。

关键词：接地网;腐蚀速率;预测;最小二乘支持向量机;遗传算法;误差校正

中图分类号：TP301                                       文献标识码：A

Abstract： It is an important measure to ensure the safe and stable operation of the power system by timely grasping and accurately predicting the operating conditions of the grounding grid and thus alerting and maintaining it. Aiming at the small sample and nonlinear characteristics of grounding grid corrosion data，and the current single prediction model has insufficient prediction accuracy，this paper proposes a combined model of improved Least Squares Support Vector Machine（LSSVM） and error correction，which is applied to grounding grid corrosion rate prediction.The method uses Genetic Algorithm（GA） to optimize the parameters of LSSVM. In order to improve the prediction accuracy of the model，the error prediction correction model is used to correct the prediction results，which reduces the possibility of maximal error and improves the stability of the prediction model. The results show that the combined model is more accurate than LSSVM in predicting the corrosion rate of the grounding grid，and more suitable for predicting the corrosion rate of grounding grid.

Key words：grounding grid;corrosion rate;prediction;LSSVM;GA;error correction

接地网属于隐蔽工程，其集工作接地、保护接地、防雷接地等功能为一体，对于电力系统的安全可靠运行和工作人员的人身安全起着至关重要的作用。及时准确地掌握和预测接地网的腐蚀严重程度，防止由于接地不良造成的危害，同时计划接地网的维修和更换的最佳时期，对于维持系统正常运行和减少经济损失意义重大。

目前，有关接地网腐蚀速率预测方面的研究成果极少。可根据接地网腐蚀速率预测物理量的不同分为两大类：（1）根据影响接地网腐蚀速率的各种因素进行预测;（2）根据原始腐蚀速率建立起系统输入与输出之间的一种线性或者非线性映射，进行直接预测。由于影响接地网腐蚀的因素有很多，土壤成分、气候和时间等都与腐蚀相关[1]，数据需要分析和简化，很难保证预测精度。本文选择直接根据接地网的原始腐蚀速率序列进行预测，但目前接地网腐蚀状态的检测主要是通过测量接地电阻、检测地网连通性以及结合局部开挖来实现的，检测周期较长，样本数据量小。由于数据本身具有小样本、非线性的特点[2]，为此，研究精度高且能够解决小样本问题的预测模型具有重要意义。

应用于金属腐蚀速率预测的方法有神经网络、灰色模型、支持向量机（Support Vector Machines，SVM）以及多种方法的组合预测模型等[3-7]。每种预测模型都有各自的优点和不足，单一方法难以达到较高的精度。神经网络理论上可以实现任何复杂的非线性映射，但是学习速度慢且失败的可能性很大;灰色模型容易操作且预测精度高，但它不考虑系统内在机理，可能出现较大的错误;SVM可将问题最终转换成二次优化问题，使其具有良好的推广能力，但SVM存在着运算费时，很依赖核函数的选择以及依靠经验选择核函数参数等缺点[8，9]。最小二乘支持向量机（Least Squares Support Vector Machine，LSSVM）是对SVM的一种改进，克服了传统神经网络的经验选择，对解决非线性和小样本等问题体现了极高的优越性，但其仍然存在依靠经验选择核函数参数的缺点。以上的预测方法均难以达到较高的预测精度[10-13]。

针对接地网腐蚀速率数据本身的小样本和非线性的特点，以及单一模型难以达到较高的预测精度，本文提出了一种结合改进最小二乘支持向量机与误差校正的组合模型，将其应用于接地网腐蚀速率预测。采用遗传算法（Genetic Algorithm，GA）优化LSSVM参数，克服了参数经验性选择导致的精度低问题;再根据原始腐蚀数据序列进行预测，得到预测值后求出预测的误差值;最后通过误差校正（Error Correction，EC）模型修正其预测结果，降低了极大误差出现的可能性，进一步提高了预测精度。通过与LSSVM、GA优化参数后的LSSVM对比分析，结果证明本文所提出的模型预测精度更高。

2   基于GA-LSSVM-EC的腐蚀速率预测

2.1   接地网腐蚀速率预测模型

目前，接地网腐蚀状态的检测主要是通过测量接地电阻、检测地网连通性及结合局部开挖来实现的，检测周期较长，样本数据量小。针对接地网腐蚀速率数据具有小样本和较强的非线性特征，本文利用LSSVM算法来建立接地网腐蚀预测模型是合理的。

由于接地网长期埋在地下环境中，会发生化学和电化学腐蚀，加之接地装置散流和杂散电流的腐蚀，故影响接地网腐蚀的因素较多，且影响因素本身具有随机性强的特点。如将这些因素都作为参数进行输入，不仅会增加计算量，也会降低算法的泛化能力，不能保证预测的精度。本文考虑数据本身具有一定的内在联系，以时间作为输入，腐蚀速率作为输出从而建立预测模型。

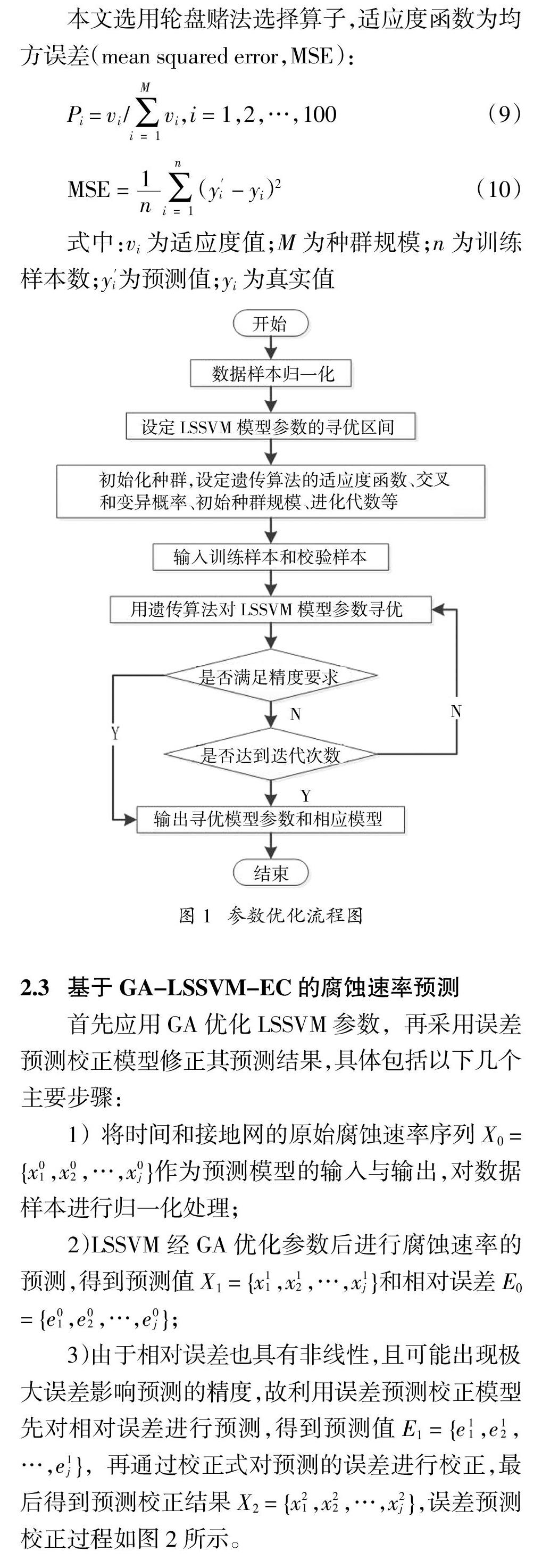
2.2   LSSVM参数优化

由经验可知，核函数宽度σ不同对应的LSSVM的拟合度也不同，惩罚系数γ同样影响着LSSVM对原始序列的逼近度。因此参数组合（σ，γ）会直接影响LSSVM预测模型的预测精度，但传统的LSSVM参数的选取经验性较强[16]。GA具有全局寻优的能力且棒鲁性较强，利用GA对LSSVM的参数进行优化具有较强的适用性。

采用GA寻找LSSVM的最优参数，寻优过程如图1所示。设种群规模为100，随机生成100个个体的初始种群P = （P1，P2，…，P100）T ，确定核函数宽度σ和惩罚系数γ的取值范围皆为（0，1024]，其中种群个体Pi = （C1，C2，…，C20）作为一个染色体，并进行二进制编码。将前10个二进制数转化成十进制数赋给σ，余下的赋给γ。各输入参数设定为：迭代次数为100通过训练样本对LSSVM进行训练，将训练误差的平方和作为种群个体的适应度值，选择的概率为0.9，变异的概率为0.1，判定终止的精度为10-5。最后得到优化后的参数组合（σ，γ）。

3   工程实例

3.1   数据来源

为了验证基于GA-LSSVM-EC组合模型的预测算法的有效性，本文选取了某变电站在2008年1月到2009年9月每月检测一次所检测的21个接地网腐蚀速率作为原始数据，如表1所示。选取前16组数据作为训练样本，后5组数据作为测试样本，分别用LSSVM、GA-LSSVM和GA-LSSVM-EC三种模型进行预测。

由图3可看出，随着迭代次数的增加适应度均方误差呈现下降的趋势（如图中黑线所示）。图3中出现了两个极大值点，可能影响预测结果的精度，同时导致预测的不稳定。本文提出的误差预测校正模型，旨在GA-LSSVM模型的基础上进一步提高预测模型的精度和稳定性。

3.3   预测结果分析

以均方误差作为目标函数，并以相对误差作为各模型的评价标准。本文分别采用LSSVM、GA-LSSVM和GA-LSSVM-EC三种模型对同一组数据样本进行仿真，接地网腐蚀速率预测结果如表2所示。

由GA-LSSVM-EC组合模型得到的预测值的相对误差分别为0.16%、0.23%、1.06%、0.37%和1.50%，平均相对误差为0.664%;GA-LSSVM模型的预测值的相对误差分别为3.11%、2.44%、1.29%、0.07%和1.64%，平均相对误差为1.71%;LSSVM模型的预测值的相对误差分别为1.39%、3.46%、5.93%、8.75%和11.84%，平均相对误差为6.276%。

图4更直观地反映了各预测模型的预测值与实际值的对比情況：与LSSVM和GA-LSSVM模型相比较，GA-LSSVM-EC组合模型的预测结果更加接近接地网腐蚀速率的实际值，预测效果更优。

图5则更直观地反映了各预测模型的预测值与实际值的相对误差。可见，单一的LSSVM模型由于参数的经验性选择，随着预测时限的增加表现出相对误差逐渐增大的趋势。GA-LSSVM模型的相对误差明显低于LSSVM模型，说明应用GA优化LSSVM参数对提高模型的预测精度有较大的帮助。GA-LSSVM-EC组合模型的预测精度明显高于GA-LSSVM模型和LSSVM模型的预测精度，证明误差预测校正模型会降低极值带来的影响，可进一步提高预测精度。由此可知，所提出的GA-LSSVM-EC组合模型对接地网腐蚀速率的预测有更好的效果。

由于变电站接地网腐蚀速率数据具有小样本和非线性等特点，故选取LSSVM建立模型，通过GA优化LSSVM参数不仅很好地解决了LSSVM模型参数盲目选取的问题，而且采用结构风险最小原则，提高了模型的预测精度。同时通过EC模型对预测结果进行校正，降低了极值对模型精度的影响，从而进一步提高了预测精度。因此GA-LSSVM-EC组合模型的预测性能更佳。

4   结   论

如何对接地网腐蚀速率进行有效预测，对保障电力系统运行具有重要的意义。提出了一种结合改进最小二乘支持向量机与误差校正的组合模型，先利用改进的最小二乘支持向量机对接地网腐蚀速率进行预测，再应用误差预测校正模型修正预测结果，大大提高了预测模型的精度和稳定性。

通过对某变电站的接地网腐蚀速率数据进行仿真分析，得到如下的结论：

（1）利用最小二乘支持向量机对接地网腐蚀速率进行预测，成功地解决了原始数据的小样本和非线性问题。

（2）最小二乘支持向量机存在着参数随机设定的问题，容易使预测结果陷入局部最优。通过遗传算法对参数进行优化，得到最优参数，从而求出全局最优解，提高了模型的精度。

（3）一种结合改进最小二乘支持向量机与误差校正的组合模型，与单一的最小二乘支持向量机模型、基于遗传算法改进的最小二乘支持向量机模型对比分析，结果表明，本文所提出的模型有着更高的预测精度，更适用于接地网腐蚀速率的预测。

参考文献

[1]    魏巍，吴欣强，柯伟，等.接地网材料腐蚀与防护研究进展[J]. 腐蚀科学与防护术，2015，27（03）：273—277.

[2]    徐德丰，程晖，莫永东，等.变电站接地网检测技术的应用[J]. 仪表技术，2015，（06）：31—34.

[3]    马良涛，董海防，朱刚，等.神经网络预测海洋环境下金属腐蚀速率的应用及研究[J]. 材料保护，2018，51（09）：42—46.

[4]    杜京义，李娜，唐小华，等.接地网腐蚀速率的非参数集群预测方法[J].计算机工程与设计，2013，34（12）： 4362—4367.

[5]    杜京义，韩娟，寇水潮，等. 基于模糊可拓层次分析的接地网腐蚀速率预测[J]. 计算机应用与软件，2014，31（06）：170—173+197.

[6]    曹洁，陈光耀，贵向泉. 基于模糊物元的熵权法在接地网腐蚀预测中的应用[J]. 腐蚀与防护，2015，36（11）： 1067—1071.

[7]    骆正山，袁宏伟. 基于误差补偿的GM-RBF海底管道腐蚀预测模型[J]. 中国安全科学学报，2018，28（03）： 96—101.

[8]    杨锡运，孙宝君，张新房，等.基于相似数据的支持向量机短期风速预测仿真研究[J]. 中国电机工程学报，2012，32（04）：35—41+21.

[9]    戴远航，陈磊，张玮灵，等. 基于多支持向量机综合的电力系统暂态稳定评估[J]. 中国电机工程学报，2016，36（05）：1173—1180.

[10]  李霄，王昕，郑益慧，等. 基于改进最小二乘支持向量机和预测误差校正的短期风电负荷预测[J]. 电力系统保护与控制，2015，43（11）：63—69.

[11]  LU N，LIU Y. Application of support vector machine model in wind power prediction based on particle swarm optimization[J]. Discrete and Continuous Dynamical Systems - Series S （DCDS-S），2017，8（06）：1267—1276.

[12]  OLAWOYIN R. Application of backpropagation artificial neural network prediction model for the PAH bioremediation of polluted soil[C]. Chemosphere，2016，161：145.

[13]  张启敏. 灰色预测模型[J]. 宁夏大学学报：自然科学版，2002，（02）：147—149.

[14]  YAN X，CHOWDHURY N A. A comparison between SVM and LSSVM in mid-term electricity market clearing price forecasting[C]// Electrical and Computer Engineering. IEEE，2013：1—4.

[15]  潘學萍，史宇伟，张弛.双加权最小二乘支持向量机的短期风速预测[J].电力系统及其自动化学报，2014，26（01）：13—17+66.

[16]  邓德慧，邓宗玮，刘闯，等. 基于改进粒子群优化LSSVM的金属腐蚀速率预测模型[J].电力学报，2019，34（01）：16—22.