融合遗传和蚁群算法的三相不平衡配电网无功优化研究

朱勇　陶用伟　李泽群

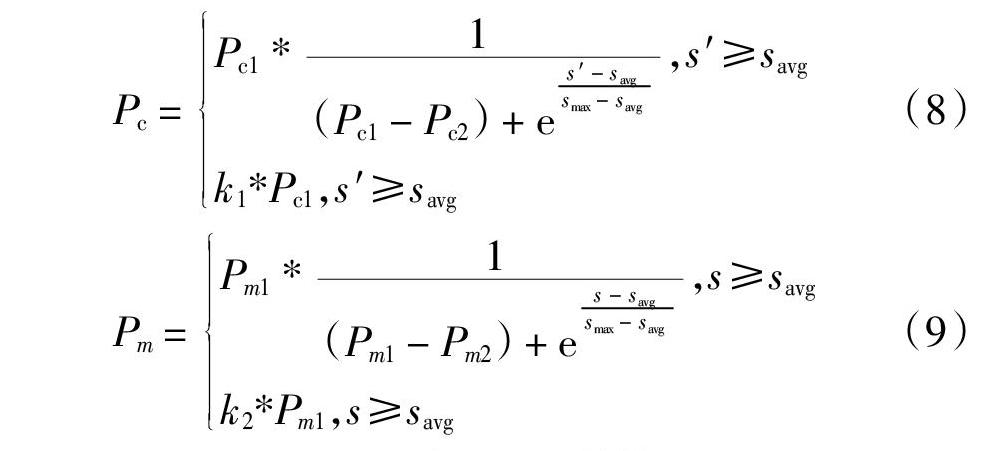
摘   要：配电网无功优化是一个多约束、多变量的高度非线性优化问题，而三相不平衡加剧了配电网无功优化的复杂程度。针对三相不平衡配电网无功优化困难的现状，提出了将遗传算法和蚁群算法相融合的智能优化方法，该方法结合了遗传算法全局优化能力强和蚁群算法局部搜索能力强的特点。为验证本方法在三相不平衡配电网无功优化的优势，建立了IEEE33节点三相配电网系统，通过与其它无功优化方法的对比分析验证了本方法的有效性和优越性。可为三相不平衡配电网的无功优化提供有效的参考和指导。

关键词：配电网;三相不平衡;无功优化;遗传算法;蚁群算法

中图分类号：TP39                                                          文献标识码：A

Abstract：Reactive power optimization of distribution network is a highly nonlinear optimization problem with multiple constraints and variables， and the three - phase imbalance aggravates the complexity of reactive power optimization of distribution network.In view ofthe difficulty of reactive power optimization in three-phase unbalanced distribution network，an intelligent optimization method combining genetic algorithm and ant colony algorithm is proposed in this paper， the method combines the characteristics of genetic algorithm's strong global optimization ability and ant colony algorithm's strong local search ability. In order to verify the advantage of this method in reactive power optimization of three-phase unbalanced distribution network， the IEEE33 node three-phase distribution system is established， the effectiveness and superiority of this method are verified compared with other reactive power optimization methods. The method in this paper can provide effective reference and guidance for reactive power optimization of three-phase unbalanced distribution network loss.

Key words：distribution network;three-phase unbalance; reactive power optimization;genetic algorithm;ant colony algorithm

配電网无功优化是电网经济优化运行领域的重要研究内容[1]，配电网无功优化可以减少网络损耗和网络运行费用，提高配电网的电压质量及其稳定性，但配电网无功优化是一个多约束、多变量的高度非线性规划问题，且目标函数不可微，使得配电网的无功优化过程十分复杂，而由于单向负荷的存在及负荷同时率的不一致，配电网普遍存在三相不平衡问题[2]，这更加加剧了配电网无功优化的困难程度。因此，为提高配电网经济运行程度，需对三相不平衡配电网无功优化进行研究。

配电网无功优化的传统数学方法有简化梯度法、内点法和非线性规划法等，但其对优化模型的精确性依赖很强，难以满足实时控制的要求，因此有学者将人工智能优化方法应用到配电网的无功优化中，取得了不错的成果，但传统智能算法均存在较大的局限性，如遗传算法局部搜索能力较差、易陷入局部最优，蚁群算法全局搜索能力较差、收敛速度较慢，相关研究人员对其进行了改进，如遗传算法采用自适应交叉、变异概率[3]，遗传算法群体进行一般组和精英组的分组[4]，蚁群算法采用信息素局部更新的策略[5]，蚁群算法初始搜索角度进行优化[6]，但仍然无法消除算法本身固有的局限性，因此部分学者将两种算法进行融合，利用算法各自的优点来弥补对方的不足之处，利用全局搜索能力强的遗传算法先对模型进行初步求解，再采用局部搜索能力强的蚁群算法对遗传算法的解进行精细搜索，如文献[7]将遗传和蚁群相结合的算法应用于的电力系统无功优化，文献[8]融合的遗传蚁群算法应用于配电网重构，均取得了很好的寻优效果，遗传和蚁群融合算法被认证为一种具有优越寻优性能的优化算法。对于三相不平衡下的配电网无功优化，目前相关的研究较少，还有很多亟需解决的问题。

提出一种遗传算法和蚁群算法相融合的智能优化方法，并将其应用到三相不平衡配电网的无功优化中，通过三相不平衡配电网仿真系统的优化对比分析对本文方法有效性和优越性进行了验证。可为三相不平衡配电网的无功优化提供有效的参考和指导。

1   配电网无功优化模型

配电网无功优化指的是基于现有的网络结构和无功补偿装置的情况下，在已知优化周期内各节点负荷大小的前提下，通过优化无功补偿装置的出力和有载调压变压器分接头的档位，使配电网某一个或多个性能指标达到最优，并满足配电网运行的相关约束条件[9]。本文在进行三相不平衡配电网无功优化时，目标函数为配电网网络损耗最小和系统负序电压最小，控制变量为有载调压变压器分接头档位、分组投切的电容器、可分组进行连续调节的静止无功补偿装置。

Cm分别表示补偿电容器m中a、b、c相投切次数，NCm max表示补偿电容器m的最大投切次数允许值，NT表示有载变压器分接头档位的调节次数， NT max表示有载变压器分接头的最大允许调节次数。

2   遗传蚁群算法原理

遗传蚁群算法是将遗传算法与蚂蚁算法相融合，获得两种算法的优点，优势互补，并克服各自的缺陷。算法的基本思想是充分利用遗传算法的随机性和快速的全局收敛性，生成一个优化问题的信息素分布，并将此分布作为蚁群算法的初始信息素分布，算法后过程则采用蚁群算法，在有一定初始信息素分布的前提下，充分利用蚁群算法并行性、正反馈性、求解效率高等特点，从而使算法的时间效率和求解效率都达到满意效果。

2.1   遗传算法和蚁群算法

遗传算法是一種基于生物自然选择与自然遗传机制的随机搜索算法[12]，其搜索过程从一组随机产生的种群的初始解开始，种群中的每个个体均为优化问题的一个解，称为“染色体”，染色体的好坏由适应度值来衡量，这些染色体会在后续寻优过程中不断进化，称为遗传。遗传算法的基本遗传算子为：选择、交叉和变异，而交叉概率、变异概率的选取对算法性能的好坏有直接影响，个体适应度越高，则种群的交叉、变异概率越高，本文采用的自适应交叉、变异概率表达式如下所示：

式中：smax、savg分别表示遗传算法种群中最大的适应度值和平均适应度值，s′、s分别表示即将要交叉的两个个体中较大的适应度值和要变异个体的适应度值，K1、K2为概率系数，取值范围[0.5，1]。

蚁群算法的基本原理蚂蚁集体觅食过程中群体协作寻找食物源[13]，是一种性能较好的模拟进化算法。蚂蚁从蚁穴出发随机选择路径寻找食物，并在沿途会释放信息素，信息素浓度越高，吸引其它蚂蚁选择该路径的概率就越大，经过蚁群一段时间的探寻，最终会聚集于一个全局最优路径。蚁群算法具有结构简单、并行性好和协同性强的优点，局部搜索能力很强，但蚁群算法且易陷入局部最优解。

2.2   遗传蚁群算法基本流程

蚁群算法采用的原理是一种正反机制，具有很强的鲁棒性能和良好的搜索能力，求解精度较高，缺点为初期信息素匮乏，算法收敛速度较慢，容易出现停滞及易陷入局部最优解，而遗传算法具有良好的全局搜索性能，但其局部搜索能力较差，算法求解精度较低，收敛速度缓慢且易陷入次优解。因此，单独使用蚁群算法或遗传算法进行优化求解都具有一定的缺陷，导致求解的结果不理想。

为了让优化算法的求解能快速地聚集在最优解附近，并且不会陷入局部最优解，本文将遗传算法和蚁群算法两种算法进行有效的融合，利用遗传算法快速随机的全局搜索能力来产生蚁群算法初期的信息素分布，在有一定初始信息素分布的前提下，再利用蚁群算法强大的局部搜索能力来获得全局最优解。遗传算法和蚁群算法的融合算法在求解精度和收敛速度方面都具有很好的优越性。

算法信息素区间设为[τmin，τmax]，当某条路径上的信息素浓度超此范围时，为防止极端情况发生，本文采用强制手段对其进行调整，信息素更新方程的表达式为

首先通过遗传算法获得优化问题的一些初始优化解，再根据所获得的初始优化解来设定初始信息素分布的值：τs = τmin + τg，其中τg的值表示遗传算法获得的初始优化解经转换后得到的信息素分布的值。

遗传蚁群算法的基本流程如图1所示。

3   遗传蚁群算法在配电网无功优化的应用

3.1   系统实例分析

为研究本文提出的融合遗传算法和蚁群算法在三相不平衡配电网无功优化中的有效性和优越性，本文以IEEE-33节点三相配电网系统为例进行测试分析[14]，并对IEEE-33节点系统进行了相应的改进：在根节点加入一台有载调压变压器，在节点8和节点23各加入一组可分相调节的无功补偿电容器组，在节点14和节点29各加入一组可分相连续调节的静止无功补偿装置SVC，改进后的IEEE-33节点三相配电网系统如图2所示，系统参数设置为：节点0为平衡节点，各节点初始电压为1.00（标幺值），有载调压变压器T变比范围为[0.90，1.10]，分接头共分10档进行调节，分组投切电容器组C1和C2各相均有有6个挡位，每相每一档位补偿功率为50 kvar，即每个电容器组每相容量为50 kvar×6，电容器组abc三相可进行独立调节，静止无功补偿装置SVC1和SVC2为abc三相可进行独立连续调节，无功补偿范围为-360～360 kvar。该配电网abc三相各相的负荷曲线图如图3所示。

3.2   配电网无功优化结果对比分析

根据遗传蚁群算法的基本流程，在MATLAB环境中编写相应的程序，并将其应用于本文改进IEEE-33节点三相配电网实例的无功优化。对于图2所示的三相配电网系统，对其进行无功优化前的配电网实际损耗为106.32 kW，当不考虑三相不平衡影响和考虑三相不平衡影响时，分别采用遗传算法、蚁群算法、退火粒子群算法和本文遗传蚁群算法进行无功优化后的结果如表1所示，图4为考虑三相不平衡影响时四种算法的无功优化收敛曲线图。

由表2可知，在对配电网进行无功优化时，考虑三相不平衡带来的影响可以明显降低配电网系统损耗值，平均降低值约10.60%，而本文遗传蚁群融合算法在四种算法中的无功优化结果是最好的。由图4可知，单纯使用遗传算法或蚁群算法均陷入局部最优解，退火粒子群算法虽然优化性能有所提高，但寻优收敛时间发生了明显的增加，而本文提出的遗传蚁群算法具有很好的寻优性能，优化后的配电网系统损耗最小，且寻优收敛时间较短。本文方法在含三相不平衡配电网系统无功优化中是有效的。

4   结   论

建立了三相不平衡下配电网无功优化的数学模型，针对三相不平衡配电网无功优化困难的现状，提出了将遗传算法和蚁群算法相融合的智能优化方法，该方法结合了遗传算法全局优化能力强和蚁群算法局部搜索能力强的特点，可以很好地获得全局最优解。为验证本方法在三相不平衡配电网无功优化中的优势，建立了IEEE33节点三相配电网仿真实例系统，通过与其它无功优化方法的对比分析验证了本方法的有效性和优越性，本方法进行三相不平衡配电网无功优化时的结果是最好的，且寻优收敛速度较快。可为三相不平衡配电网系统无功优化提供有效的参考和指导。

参考文献

[1]    HUA Z. Reactive power optimization of distribution network based on improved genetic algorithm[J]. Electrical Engineering， 2012.

[2]    周虎， 陈佳黎， 鲜龙，等. 电网三相不平衡下农网低电压治理的研究[J]. 电网与清洁能源， 2015， 31（11）： 13—18.

[3]    王振浩， 李文文， 陈继开， 等. 基于改进自适应遗传算法的分布式电源优化配置[J]. 电测与仪表， 2015， 52（5）：30—34.

[4]    DEVARAJ D. Improved genetic algorithm for multi‐objective reactive power dispatch problem[J]. International Transactions on Electrical Energy Systems， 2010， 17（6）：569—581.

[5]    HORSMANS Y， TENNSTEDT D， CORNU C， et al. An improved ant colony algorithm for fuzzy clustering in image segmentation[J]. Neurocomputing， 2007， 70（4）：665—671.

[6]    夏亞梅， 程渤， 陈俊亮， 等. 基于改进蚁群算法的服务组合优化[J]. 计算机学报， 2012， 35（2）：270—281.

[7]    周申培， 严新平. 遗传蚁群融合算法及在不确定性无功优化中的应用研究[J]. 电力系统保护与控制， 2010， 38（24）.

[8]    赵金亮. 基于自适应遗传算法和蚁群算法融合的配电网重构[D]. 兰州理工大学， 2011.

[9]    赵昆， 耿光飞. 基于改进遗传算法的配电网无功优化[J]. 电力系统保护与控制， 2011， 39（5）：57—62.

[10]  BAJO C G， HASHEMI S， KJSAER S B， et al. Voltage unbalance mitigation in LV networks using three-phase PV systems[C]// IEEE International Conference on Industrial Technology. IEEE， 2015：2875—2879.

[11]  张聪誉， 陈民铀， 罗辞勇， 等. 基于多目标粒子群算法的电力系统无功优化[J]. 电力系统保护与控制， 2010， 38（20）： 153—158.

[12]  赵俊普， 殷进勇， 金同标，等. 遗传蚁群算法在云计算资源调度中的应用[J]. 计算机工程与设计， 2017（3）：693—697.

[13]  RAJENDRAN C， ZIEGLER H. Ant-colony algorithms for permutation flowshop scheduling to minimize makespan/total flowtime of jobs[J]. European Journal of Operational Research， 2007， 155（2）：426—438.

[14]  DZAFIC I， NEISIUS H T， GILLES M， et al. Three-phase power flow in distribution networks using Fortescue transformation[J]. IEEE Transactions on Power Systems， 2013， 28（2）：1027—1034.