基于孔隙结构参数的相控渗透率地震预测方法
2019-11-05甘利灯王峣钧罗贤哲张明李贤斌戴晓峰杨昊
甘利灯,王峣钧,罗贤哲,张明,李贤斌,戴晓峰,杨昊
(1.中国石油勘探开发研究院,北京 100083;2.电子科技大学,成都 611731)
0 引言
渗透率是刻画储集层特征和地下流体流动性的重要参数,对开发方案设计、地下流体特征研究均具有重要作用,因此对地下渗透率参数进行预测具有重要意义[1]。目前,石油工业界储集层渗透率预测仍主要以测井数据和岩心分析为主,方法包括压汞实验分析、核磁共振分析等,但是这些实验手段相对昂贵且观测数据所覆盖储集层范围有限,难以实现对储集层渗透率大尺度横向分布规律的研究。地震数据提供了丰富的地层横向展布信息,利用地震数据进行储集层渗透率预测,可为储集层预测提供有效的渗流场信息,对储集层评价和油气藏开发具有重要意义。
利用地震数据进行储集层渗透率预测一直是储集层预测的前沿和难点问题,众多学者对此进行了诸多研究[2],主要技术方法有经验法、地震属性分析法[3-4]和地质统计学模拟法等。经验法即通过井中实测孔隙度和渗透率散点交汇图进行拟合,将拟合公式应用于实际地震数据中。在岩石孔隙较为复杂时,往往很难得到孔隙度与渗透率的线性回归关系,导致该二元线性回归方法存在较大误差[2]。地震属性分析法即采用神经网络等方法将地震属性与渗透率建立非线性神经网络关系,然后将空间分布的地震属性体转换为渗透率体[5],该技术可能存在因渗透率样本较少导致神经网络过拟合现象。地质统计学模拟方法即采用协克里金插值方法,以井点渗透率为主变量,通过次变量地震属性趋势约束对渗透率曲线进行插值,该方法要求井资料丰富,而且要求井在平面上分布较均匀[5]。
综上所述,目前采用地震数据预测渗透率仍存在诸多难点,究其原因,主要是渗透率与孔隙度不是单纯的一一对应关系,还受到孔隙结构的影响。不同孔隙结构的岩石,孔隙度与渗透率对应关系存在明显差异,只有结合储集层孔隙结构进行渗透率预测才能降低多解性,提高预测精度[6]。
前人研究表明,储集层弹性参数可以用于储集层孔隙结构预测,比如通过弹性参数和岩石物理模型可以反演孔隙纵横比[7],通过弹性参数和岩石物理模型反演骨架柔度因子(frame flexibility factor)[8]。近年来,有研究人员探索了将孔隙度和骨架柔度因子结合进行渗透率预测的新思路,在美国德克萨斯、四川盆地普光气田等碳酸盐岩储集层中取得了较为成功的应用[8-9]。该方法首先在测井数据中计算得到骨架柔度因子,结合骨架柔度因子和岩石薄片对岩石进行分类,然后在每一类岩石中进行孔隙度和渗透率的回归计算[8,10-12]。该技术通过结合孔隙结构参数有效降低了渗透率预测的多解性,但实际应用过程中仍然存在诸多问题,主要表现在:①现有方法采用骨架柔度因子数据直接分段进行岩石分类过于简单,实际在岩石分类过程中有必要综合考虑孔隙度、速度等信息,提高岩相分类准确性;②现有方法仅通过孔隙结构参数进行分类,在分类后直接采用孔隙度对渗透率进行线性回归过于简单,没有考虑到孔隙结构和速度信息对渗透率预测的影响;③现有基于孔隙柔度的渗透率预测大多仅限于测井数据,目前利用地震数据进行空间渗透率预测的研究较少;④现有研究利用岩心薄片对柔度因子分类准则进行标定,实际应用过程中可能存在岩心薄片数量有限等问题,亟需探索采用其他数据进行分类预测的方法。针对以上问题,本文在数据分析基础上探索出一套基于地震数据和测井数据的渗透率空间分布预测新方案,即采用储集层段孔隙度、弹性参数及骨架柔度因子进行岩相分析,在每类岩相中采用孔隙度、纵横波速度及骨架柔度因子进行多元回归得到预测渗透率,实际应用验证了该方法的有效性,为储集层渗透性参数空间分布预测提供了可行思路。以上研究方案突出了“相”控和孔隙结构参数在储集层渗透率预测中的重要作用,这也是当前复杂储集层预测重要的发展方向。
1 方法与原理
本文中使用方法主要涉及骨架柔度因子计算、岩相分类和多元回归方法。由于多元回归方法较为常见不再赘述,下面仅对骨架柔度因子和基于集成学习(Adaboost)的岩相分类方法进行介绍。
1.1 骨架柔度因子计算
骨架柔度因子是 Sun[13]推导的新的岩石物理模型中引入的参数,主要包含体骨架柔度因子(γ)和剪切骨架柔度因子(γμ)[13]。这些骨架柔度因子参数可以用于描述不同形状和大小孔隙对地层弹性属性的影响,其中体骨架柔度因子解释了在应力条件下的体应变,剪切骨架柔度因子解释了剪切形变[11]。主要公式如下:

通常流体对体积模量影响较大,导致实际体骨架模量难以计算,而剪切模量不受流体影响,此时可将干岩石剪切模量近似等价为岩石总体剪切模量,即μ=μd。有研究表明,在低孔隙度区域,不同孔隙类型的纵波速度差异相对较小,此时剪切柔度因子对于孔隙形态变化有更加明显的响应[11];因此在本文研究中主要采用剪切柔度因子。基于以上公式,可以得到剪切柔度因子计算公式:

式中孔隙度可以通过密度计算得到,也可以通过计算岩石总孔隙度获得,基质剪切模量可以通过实验室岩心测试获得。通常在地震数据中可以先进行叠前反演得到纵横波速度、密度,采用岩石物理约束反演或地震属性预测方法得到孔隙度,带入上述公式中即可算出剪切柔度因子。
1.2 基于集成学习方法的岩相分类
岩相分类是测井解释中的一项基本工作,人工解释工作量大,因此采用机器学习方法进行分类成为当前岩相分类发展的重要趋势。目前实际应用比较多的是支持向量机(SVM)岩相分类方法,该方法核心思想是找到一个超平面将数据进行区分,但是实际应用过程中数据复杂度较高,单纯采用SVM方法很难实现岩相准确分类,本文采用集成学习方法进行岩相分类。
集成学习方法是一种自适应权重更新算法,该算法首先训练一些基本分类器,然后给训练样本赋予权重,每次训练新分类器时,会利用当前分类器处理结果更改训练样本权重,使被正确分类样本权重减小,错误分类样本权重增加,使分类器模型更为关注那些错误分类的样本,循环迭代即可有效提升普通分类器分类效果,其具体算法流程见图1[14]。为表明应用效果,笔者利用研究区FUD7井和 FUD6井进行了岩相分类测试,并与SVM分类效果进行了对比(见图2),图2中岩相分类数为两类,分别代表砂岩(黄色)和泥岩(蓝色)。从分类精度对比可见,SVM 分类精度(FUD7井为92.18%,FUD6井为89.43%)要高于SVM方法(FUD7井为70.78%,FUD6井为64.63%),因此后文均采用集成学习方法进行岩相分类。
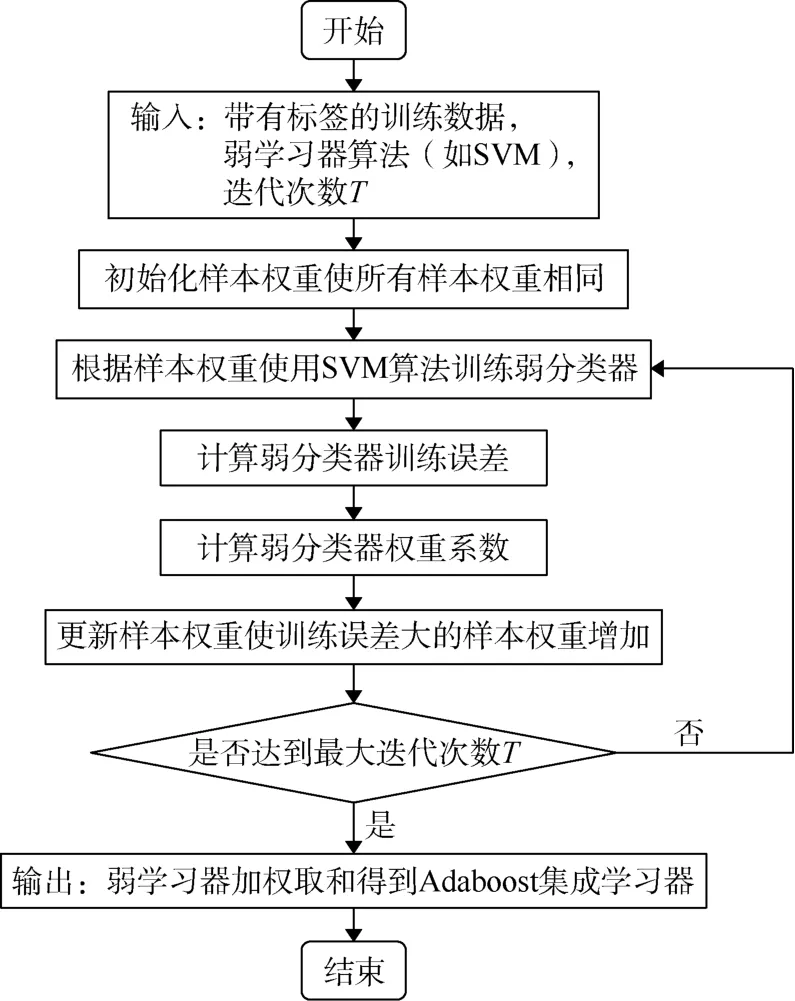
图1 集成学习算法流程图
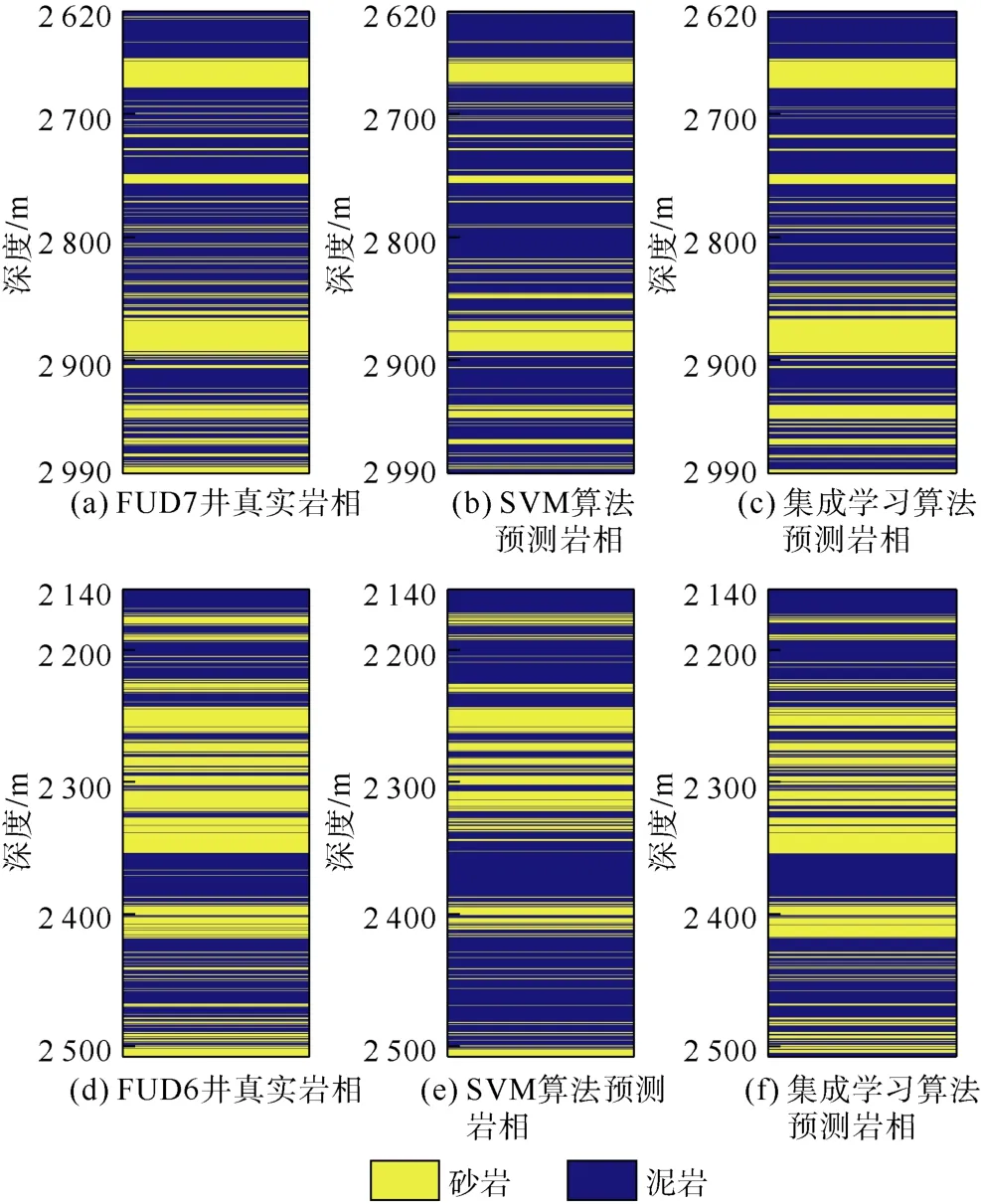
图2 研究区FUD7井(训练数据)与FUD6井(测试数据)SVM及集成学习岩相分类对比
2 测井资料渗透率预测
2.1 研究区概况及储集层地球物理特征分析
研究区位于准噶尔盆地中央坳陷带东部的阜东斜坡区,油藏类型主要为岩性-地层油气藏,侏罗系自下而上可划分为八道湾组(J1b)、三工河组(J1s)、头屯河组(J2t)和齐古组(J3q)等,头屯河组底界向东逐渐抬升、尖灭,与上覆白垩系砾岩不整合接触。该区主要勘探目的层为头屯河组,整体为水退沉积,以河流-三角洲沉积为主。岩性为灰色、灰绿色、褐色中厚层细砂岩、粉砂岩与褐色、浅紫色中厚层泥岩互层,砂岩孔隙度为3.00%~30.25%,平均为16.65%,渗透率为(0.017~696.610)×10-3μm2,平均为 4.13×10-3μm2。
该工区典型井FUD7井测井曲线如图3所示。岩石物理分析表明,研究区头屯河组砂岩与泥岩纵波速度和密度差异小,波阻抗叠置严重,叠后反演难以区分岩性,而纵横波速度比差异较大,可以较好区分;与致密干砂岩相比,高孔隙度砂岩表现为低纵波阻抗、低纵横波速度比特征。由图3测井渗透率和剪切柔度因子曲线对比可发现,孔隙度和渗透率对应关系不明显,但是渗透率与剪切柔度因子具有一定对应关系,高渗层段基本对应低剪切柔度因子,反之则不一定成立,即低剪切柔度因子层段不一定是高渗的。
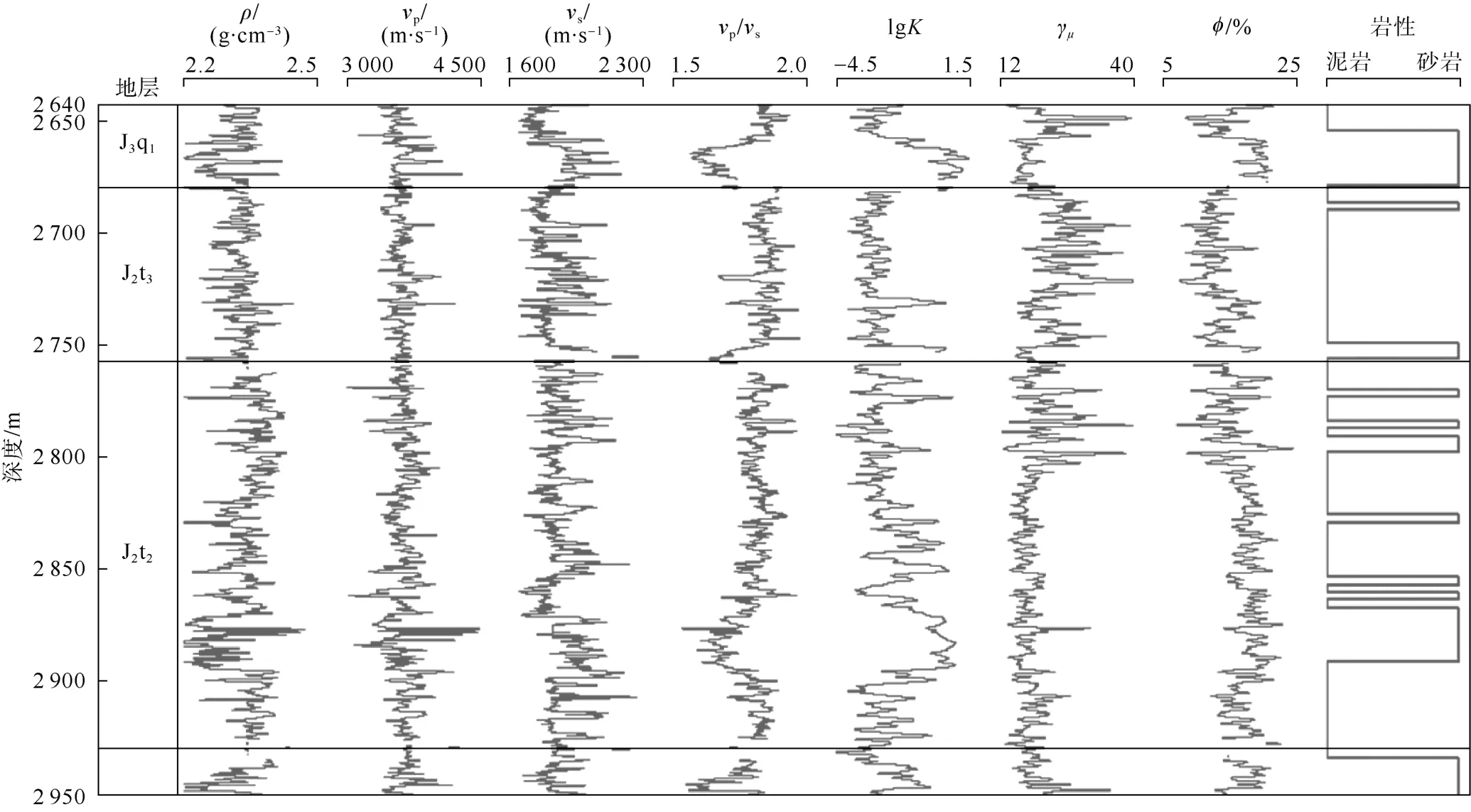
图3 研究区FUD7井头屯河组上部测井曲线图
在Huang等提出的基于柔度因子的测井渗透率预测中[11],其采用柔度因子与岩石薄片建立联系,然后通过柔度因子硬阈值划分区域,最后在每一个划分区域中进行孔隙度-渗透率关系拟合。以FUD7井为例,采用孔隙度-渗透率-柔度因子交会图方式分析该方法可行性。图4为FUD7井头屯河组上部孔隙度-渗透率-剪切柔度因子交会图,由于该对应井段没有岩心薄片,因此将柔度简单划分为 8段进行显示。可以发现,整体上单个孔隙度可能和多个量级渗透率存在对应关系,孔隙度和渗透率单一线性关系不明显;结合剪切柔度因子来看,剪切柔度因子对孔隙度-渗透率具有一定区别但不够明显,直接采用硬阈值方法很难实现区域划分。从该井孔隙度-渗透率-岩性交会图(见图5)分析可以发现,渗透率和孔隙度在不同岩相上分布存在重叠。从剪切柔度因子-渗透率-岩性交会图(见图6)分析可以发现,柔度和渗透率关系在不同岩相上也存在重叠,如果不区分岩相,也很难有效分析柔度因子与渗透率的关系。由此可以初步可以判定,单纯采用柔度因子划分区域后进行孔隙度-渗透率回归或者单纯采用孔隙度-渗透率经验关系进行渗透率预测都很难取得好的效果。由于储集层岩相对孔隙度-渗透率-剪切柔度因子关系影响较大,因此本论文拟采用剪切柔度因子与岩相相结合的渗透率预测新方案。

图4 目标工区FUD7井头屯河组上部孔隙度-渗透率-剪切柔度因子交会图

图5 目标工区FUD7井头屯河组上部孔隙度-渗透率-岩性交会图

图6 目标工区FUD7井头屯河组上部剪切柔度因子-渗透率-岩性交会图
2.2 基于剪切柔度因子的多元回归分析
由以上分析可知,渗透率与孔隙度之间相关性差,为此尝试引入其他弹性参数来改善它们之间的线性回归关系,并探讨柔度因子对渗透率预测的影响。为了将该方法能应用于地震数据,笔者选择纵波速度、纵横波速度比、剪切柔度因子和孔隙度用于渗透率预测(由于密度反演可靠性低,在此不予考虑),进行如下几类测试:①孔隙度对渗透率回归;②孔隙度加剪切柔度因子对渗透率进行多元回归,然后将剪切柔度因子依次替换为纵波速度、纵横波速度比,对渗透率进行多元回归,分析剪切柔度因子对渗透率回归的影响;③利用孔隙度、纵波速度、纵横波速度比对渗透率进行预测;④孔隙度、纵波速度、纵横波速度比和剪切柔度因子对渗透率进行多元回归预测。此处笔者选择FUD7井作为训练井,FUD6井作为测试验证井。表1为以上测试计算曲线的均方误差(MSE)和决定系数(R2),其中决定系数为相关系数的平方,决定系数越大表示预测结果与真实结果相关程度越高。可以发现,单纯采用孔隙度进行渗透率预测误差较大,加入纵波速度、纵横波速度比和剪切柔度因子后可以有效改善预测精度,但是剪切柔度因子与孔隙度结合对渗透率预测精度提高更为明显(加入剪切柔度因子后预测误差为0.776 5,要小于其他方法计算结果);如果将孔隙度、纵波速度、纵横波速度比和剪切柔度因子都用于多元回归误差最低,预测误差为0.742 1。从以上分析可以得出结论,即采用弹性参数、剪切柔度因子多元回归可以提高渗透率预测精度,剪切柔度因子相比纵波速度、纵横波速度比等常规弹性参数对渗透率更加敏感,对于提高渗透率预测精度意义更大。图7显示了以上方法在FUD7井和 FUD6井预测的渗透率与真实渗透率对比,其中图7a、图7b为单纯采用孔隙度预测渗透率结果,图7c、图7d为孔隙度+剪切柔度因子预测渗透率结果,图7e、图7f为孔隙度+纵波速度+横纵波速度比+剪切柔度因子渗透率预测结果。
进一步分析图7可以发现,预测结果在部分区域仍存在较大误差,分析该误差段岩相发现其主要是非储集层的泥岩段(FUD6井2 320~2 350 m深度段),在泥岩段,渗透率普遍较小,但剪切柔度因子与砂岩段有重叠,这是导致多元回归存在误差的主要原因,因此在渗透率预测中应该考虑岩相变化对渗透率预测的影响。

表1 多元回归均方误差及决定系数统计

图7 训练井(FUD7井)和测试井(FUD6井)渗透率预测结果对比图
2.3 基于剪切柔度因子的相控多元回归分析
在前述实验基础上,笔者对岩相变化对渗透率预测的影响进行了分析,为避免岩相预测误差的影响,先直接利用录井获得的真实岩相。此次仍采用 FUD7井进行训练,FUD6井进行预测。具体步骤为:对于训练井中不同岩相对应数据分别计算回归关系,然后将训练得到的对应岩相回归关系应用到预测井中获得渗透率预测结果。图8为仅采用孔隙度进行相控训练和预测获得的渗透率与测井渗透率的对比图;图9为利用孔隙度、纵波速度、纵横波速度比等 3种参数进行相控回归训练和预测获得的渗透率和测井渗透率对比图,图10为利用孔隙度、纵波速度、纵横波速度比和剪切柔度因子等 4个参数进行相控回归训练和预测获得的渗透率与测井渗透率对比图。以上相控渗透率预测均方误差及决定系数见表1。与前面不分相多元回归预测误差和决定系数对比发现,相控前后预测误差有不同程度减少,决定系数有不同程度提高,而且回归参数包含剪切柔度因子后,预测误差减少幅度和相关系数提高幅度都是最大的,也即岩相控制下的包含弹性参数和剪切柔度因子的多元回归是储集层渗透率预测的可行方案。

图8 仅采用孔隙度进行相控训练(FUD7井)和预测(FUD6井)获得的渗透率与测井渗透率的对比图

图9 采用孔隙度+纵波速度+纵横波速度比训练(FUD7井)和预测(FUD6井)获得的渗透率与测井渗透率的对比图

图10 采用孔隙度+纵波速度+纵横波速度比+剪切柔度因子训练(FUD7井)和预测(FUD6井)获得的渗透率与测井渗透率的对比图
前述分析中所使用的是真实岩相,但实际应用时只能通过已知弹性数据进行岩相划分。为了评价岩相分类误差对渗透率预测的影响,笔者设计如下 3种参数组合:①孔隙度;②孔隙度+纵波速度+纵横波速度比;③孔隙度+纵波速度+纵横波速度比+剪切柔度因子。基于 3种参数组合,利用支持向量机方法进行岩相划分,在岩相划分基础上利用各自参数组合进行相控多元渗透率回归和预测。同样采用 FUD7井作为训练井,FUD6井作为测试井。表2为录井岩相分类基础上渗透率回归和预测结果与常规方法(支持向量机方法)岩相分类后渗透率回归和预测的误差对比。从岩相分类效果看,剪切骨架柔度因子对岩相划分的精度影响不大,因此在渗透率预测时可以先采用常规弹性参数对岩相进行分类,但前面已经指出,岩相分类方法对结果影响很大。从渗透率预测误差对比可以发现,采用SVM方法获得的岩相分类精度较低(约70%),此时无论增加常规弹性参数还是剪切柔度因子进行训练和预测,渗透率预测的误差改善很小(见表2),即岩相划分精度对渗透率预测精度影响很大。将表2中基于SVM分相的预测结果与表1不分相预测结果对比可以发现,分相预测结果甚至比不分相时预测结果误差更大(FUD6井不分相预测误差为0.935 6,采用SVM分相后预测误差为2.062 7),由此可见,可靠的岩相分类是渗透率预测的基础,增加纵横波速度等弹性参数可以提高岩相划分精度,但岩相分类方法选择尤为重要。在高精度岩相划分的基础上,增加纵波速度、纵横波速度比等常规弹性参数可以提高相控渗透率预测的精度,但不如增加剪切柔度因子效果明显。

表2 岩相划分精度对相控渗透率预测的影响
3 地震资料渗透率预测
3.1 预测过程
经过上述分析可以得到利用地震资料进行渗透率预测的方案:先利用叠前地震反演结果计算孔隙度和剪切柔度因子,再利用叠前反演结果、孔隙度、剪切柔度因子进行储集层岩相划分,在分类基础上利用以上几种属性进行多元回归,实现渗透率预测。图11为计算得到的剪切柔度因子连井剖面,图12为岩相分类剖面,图13为对数渗透率连井剖面。

图11 研究工区头屯河组下段剪切柔度因子连井剖面
3.2 预测效果分析
为了验证上述预测方法的有效性,笔者仍以FUD7为训练井,选择 FUD071井和FUD6井进行验证,从剖面与嵌入的测井渗透率对比来看,对数渗透率符合程度较高(见图13),预测误差在2个色标以内,即渗透率预测误差基本可以控制在1个数量级以内。
由图13可见,FUD7井产油层与FUD071井水层孔隙度高,渗透性好,两口井间砂体是连通的,因此处于低部位的FUD071井产水,而处于高部位的FUD7井产油,同时,该套砂体向东高部位逐渐减薄,并尖灭于FUD7井和FUD6井之间,因此FUD6井干层与FUD7井产油层属于不同期次沉积的砂体。FUD7井低产油层虽然砂体物性好,但由于砂体较薄、分布范围小,导致产量低。
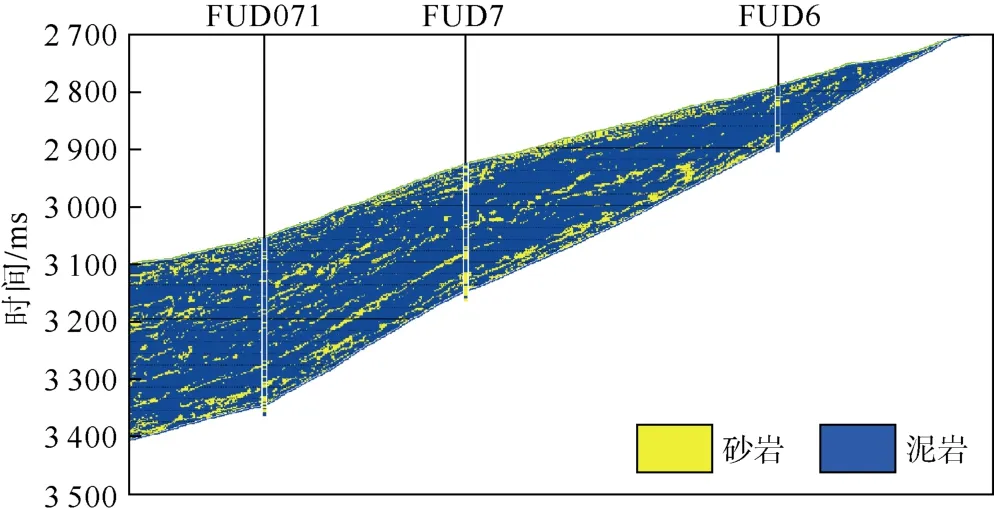
图12 研究工区头屯河组下段岩相分类连井剖面
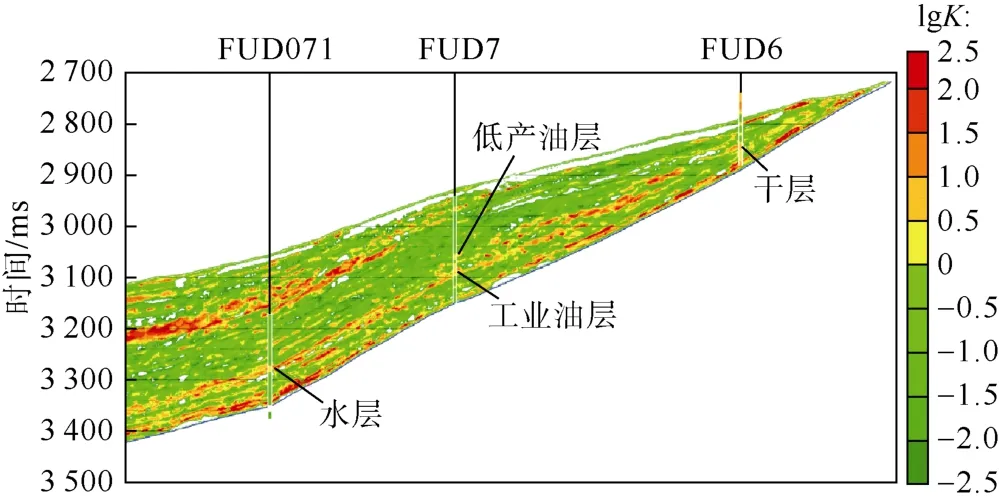
图13 研究工区头屯河组下段对数渗透率连井剖面
4 结论
通过测井数据渗透率预测试验表明,与常规弹性参数相比,表征孔隙结构的剪切骨架柔度因子对渗透率更加敏感,可以更好地用于渗透率预测;岩相分类准确性对渗透率预测精度影响很大,是渗透率预测的基础,在此基础上形成的基于剪切骨架柔度因子的相控渗透率地震预测方法可以将渗透率预测精度控制在一个数量级内,为利用地震资料开展渗透率空间预测提供了一种有效方法。下一步需要研究更高精度的岩相分类方法,以及对渗透率更加敏感的孔隙结构参数提取方法。
符号注释:
MSE——均方误差,无因次;K——渗透率,10-3μm2;Kd——干岩石体积模量,GPa;Ks——基质体积模量,GPa;vp——纵波速度,m/s;vs——横波速度,m/s;p——体积模量,GPa;R2——决定系数,无因次;T——算法迭代次数,无因次;ρ——密度,g/cm3;γ——体骨架柔度因子,无因次;γμ——剪切柔度因子,无因次;φ——孔隙度,%;μ——弹性模量,GPa;μd——干岩石弹性模量,GPa;μs——基质弹性模量,GPa。
