岩心颗粒彩色图像的多维特征KFCM聚类分割算法
2019-11-05
(上海理工大学 能源与动力工程学院; 上海市动力工程多相流动与传热重点实验室,上海 200093)
岩心是矿物开采、石油勘探等地质工程研究中极其重要的实物地质资料。岩心分析是指针对采用各种仪器设备(如电镜扫描仪、偏光与电子显微镜等)获取的岩心图像进行观测与模拟试验分析,在矿产开发与油气地质研究中具有重要作用。岩心颗粒图像分割在岩心分析过程中占据着重要地位。岩心颗粒与背景区域的分割准确性直接决定了颗粒目标识别和粒度分布信息的提取的准确性。岩心分析结果可作为油气盆地地层和沉积环境的探索与开发的直接依据[1-2]。
国内外学者提出了许多种岩心图像分割算法和技术来获取岩层物性特征、孔隙结构和颗粒粒度分布等信息。Zhou等[3]结合形态学运算的优点,提出一种改进的分水岭算法,对岩心颗粒分割结果区域合并避免了过分割现象;Samet等[4]针对岩石图像数据定义了一种新的模糊规则图像分割技术,实现了颗粒边缘检测;陈本廷等[5]应用超像素对岩心偏振图像进行初始化分割,再利用超像素区域的颜色信息进行K均值聚类分割;Fazekas等[6]利用完全卷积神经网络(FCN)进行岩心图像分割,并基于深度学习的方法去除岩心图像二次色彩的伪影。
虽然针对岩心图像分割方法的研究已取得一定的成果,但大都在分割过程很少考虑到图像的纹理特征。因此,本文中充分利用颗粒图像中丰富的纹理、颜色和空间位置特征信息,针对岩心颗粒的显微偏振图像和电镜扫描图像进行岩心颗粒的彩色图像分割算法的研究,从而提高岩心颗粒的粒度分布信息提取的准确性。
1 彩色图像分割的原理与流程
在岩心分析过程中,需要从岩心颗粒彩色图像中提取相关特征信息,确定图像的像素点是否属于同种特征或特征相似,进而把图像像素点分成不同的子集,判定像素集属于岩心颗粒或背景。但仅仅利用色彩信息对岩心颗粒彩色图像进行分割,往往会导致欠分割现象,岩心颗粒无法完全识别出来。因此,必须综合利用局部纹理特性和空间位置关系,确保属于同一颗粒的像素点的颜色、纹理特征均相似、空间位置上相邻。
1.1 颜色特征空间的选取
颜色特征的描述依赖于所选取的色彩空间,针对图像处理常用的色彩空间RGB、HSV、HSI和CIELAB等,研究学者做过大量对比性图像分割试验,分析了在各类颜色空间上图像分割的适用性[7-9]。
CIELAB色彩模型是一种基于生理特征的均匀色彩空间。CIELAB色彩空间上不同像素点的亮度信息分量为L*,颜色特征信息分量分别为a*和b*,直接使用这3个分量之间的几何距离来实现不同颜色之间的对比, 通过数字化形式直观地描述了人眼的视觉感知,可以有效地应用于测量微小色差。因此选取CIELAB色彩空间对岩心颗粒彩色图像进行分割研究。
在CIELAB色彩空间中,亮度信息L*对于颗粒识别具有一定的重要性,以特征向量[L*,a*,b*]的形式表示颜色信息可以通过亮度信息优化那些仅利用颜色信息无法完全分割的颗粒图像。它把颗粒图像中每个像素点近似为三维空间上的一点,并将两像素点之间的欧式距离ΔE作为颜色特征相似性测量判据:
(1)
1.2 二维Gabor滤波器原理
目前,纹理特征提取方法应用广泛的主要有灰度共生矩阵(GLCM)、局部二进制模式(LBP)、高斯马尔可夫随机场(GMRF)和Gabor滤波变换等。其中,Gabor滤波器具有时域(或空域)和频域的联合最佳分辨率,能够很好地模拟人类视觉感知系统的特点[10],其最重要的优点是对于旋转、缩放和平移的不变性,而且对图像噪声干扰和光照条件改变具有很强的鲁棒性[11-12],因而选用Gabor滤波器组在频域上从不同尺度和方向提取岩心颗粒灰度图像中的相关纹理特征。
二维Gabor滤波器函数实质是二维高斯核函数和正弦平面波的乘积,其数学表达式[13]为
g(x,y,λ,θ,ψ,σ,γ)=
(2)
x′=xcosθ+ysinθ,
y′=-xsinθ+ycosθ,
(3)
式中:x和y分别为高斯核的坐标信息;λ为正弦函数波长;θ为Gabor核函数的方向;ψ为相位偏移;σ为高斯函数标准差;γ为空间宽高比。
将二维Gabor滤波器函数对应的实数部分gR与虚数部分gI分别与岩心灰度图像f(x,y)进行卷积运算,可得到滤波后Gabor幅值(能量)特征图像S(x,y)的数学表达式为
(4)
1.3 Gabor纹理特征提取流程
在提取岩心颗粒图像纹理特征时,需选取一个合适的Gabor滤波器组,在频域的不同尺度、 不同方向上提取相关特征。 由于各种不同方向和尺度的Gabor滤波器是自相似的,因此可以从母小波函数g(x,y)经过尺度变换和旋转变换来构建Gabor滤波器组。
选取母小波滤波函数的波长初始值为4个像素值,Gabor核函数方向为0;然后母小波函数经过尺度变换和旋转变换构建5个尺度、 8个方向的Gabor滤波器组,其中波长范围为4~16像素,方向为0~2π。 随着卷积模板的增大,Gabor滤波器变换提取的特征逐渐由全局特征向局部特征变化,对比滤波结果选择卷积模板大小为35×35像素。将岩心颗粒的彩色图像从不同尺度和方向上利用Gabor滤波器组提取纹理特征的流程如图1所示。

图1 Gabor滤波器组提取纹理特征流程图Fig.1 Flow chart of Gabor filter banks used to extract texture features
首先,将岩心颗粒的彩色图像转换为灰度图像f(x,y), 彩色图像像素大小为576×768,如图2所示。
然后利用5个尺度、8个方向的Gabor滤波器组对岩心灰度图像进行卷积运算,Gabor滤波器组输出的40张幅值特征图像如图3所示。
最后,由于采用40个Gabor滤波器提取岩心颗粒图像的纹理信息,对于图2中大小为576×768像素的岩心灰度图像,获取的纹理特征向量维度为576×768×40,维数太大且存在许多不需要的特征信息,因此对图3所示的多尺度、多方向Gabor滤波器组输出滤波结果求均值,将得到的特征均值向量归一化为零均值和单位方差,作为岩心颗粒图像纹理特征T,图4为Gabor滤波器组最终输出的幅值特征均值图像。
1.4 多维特征KFCM聚类岩心图像分割流程
核模糊C均值(KFCM)[14]聚类算法中基于核函数思想,把岩心颗粒彩色图像像素点特征信息映射至高维特征空间后,原线性不可分数据信息变得可分或者接近于线性可分,改善了FCM聚类分割思想对于岩心图像中非球形分布数据的性能,进而实现岩心颗粒图像数据更准确的聚类分析。当选用高斯核函数时,在高维特征空间中KFCM聚类的目标函数[15]为
(5)
(6)
式中:c为聚类数目;n为像素点个数;m为加权指数;vj为第j个聚类中心;uij为像素点xi被分配在第j类的隶属度;K为高斯核函数。

a 岩心颗粒原图b 灰度图像图2 岩心颗粒的彩色图像转换为灰度图像Fig.2 Color image of core particles converted into grayscale image

图3 Gabor滤波器组输出的40张幅值特征图像Fig.3 40 value feature images output of Gabor filter bank
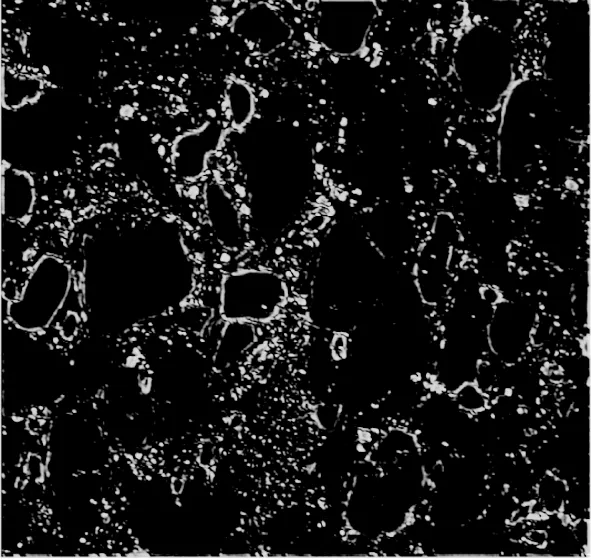
图4 Gabor滤波器组输出的幅值特征均值图像Fig.4 Gabor filter bank output amplitude characteristic mean image
KFCM聚类的目标函数经拉格朗日乘子法最小化,推导得出算法迭代过程中的聚类中心vj和隶属度uij为
(7)
(8)
综合从岩心颗粒彩色图像中提取的颜色信息(L*、a*、b*)、 Gabor纹理特征T和空间坐标(Sx,Sy)3种特征信息,岩心颗粒彩色图像多维特征KFCM聚类分割算法具体过程如下:
1)将岩心颗粒彩色图像像素点包含的特征信息量化为特征向量,每一像素点表示为特征向量[L*,a*,b*,T,Sx,Sy],作为样本数据输入;
2)参数初始化设置,设置算法的最大迭代次数和结束阈值ε,确定聚类数目c,加权指数m和高斯核尺度参数σ;
3)使用0~1之间的随机数初始化隶属度,且满足式(6)的约束条件;
4)根据式(7)计算聚类中心vj;
5)由公式(5)获得KFCM聚类分割的目标函数值。如果此时超过最大迭代次数,或者相对上次迭代目标函数值的变化量低于阈值ε,那么算法迭代过程结束;
6)否则,使用公式(8)计算新的隶属度函数并返回步骤4继续执行迭代。
岩心颗粒图像的多维特征KFCM聚类分割算法流程如图5所示。
按照图5所示的图像分割流程,在岩心颗粒的显微偏振图像和扫描仪采集图像上进行分割实验。分割过程中遵循同一聚类内相似度尽可能大、不同聚类之间相似度尽可能小的原则,比较在不同聚类数目下目标损失函数,以此衡量聚类分割后的结果,从而确定适用于当前类型的岩心颗粒彩色图像的最佳聚类数目。
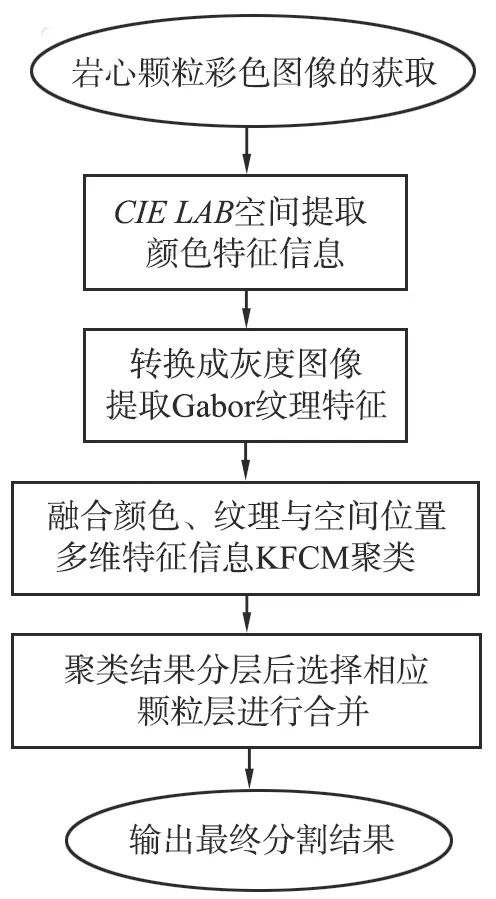
图5 岩心颗粒图像的多维特征KFCM聚类分割算法流程Fig.5 Multi-dimensional feature KFCM clustering segmentation algorithm for core particle image
2 仿真试验与结果
2.1 试验目的和条件
为验证算法可行性,首先对比分析多维特征KFCM聚类分割算法、超像素优化的基于颜色信息的K均值聚类分割方法[5]和基于HSV空间V分量分割方法[1]这3种岩心图像分割算法的分割效果;然后,应用多维特征KFCM聚类分割算法在不同类型的岩心颗粒彩色图像上进行分割试验。不同类型的岩心颗粒彩色图像均利用偏光显微镜、岩心扫描仪采集而得。
试验的硬件环境条件为:Intel(R) Core(TM) i5-3230M型CPU,内存4G;软件环境为:Window10操作系统,Matlab R2017a。
2.2 不同算法分割效果的对比
分别应用多维特征KFCM聚类分割算法、超像素优化的基于颜色信息的K均值聚类分割方法和基于HSV空间V分量分割方法,在图2所示的岩心颗粒彩色图像上进行分割试验,不同算法类型的分割结果如图6所示。

a KFCM聚类分割算法b K均值聚类分割算法c V分量分割算法图6 不同算法的彩色图像分割效果Fig.6 Results of different algorithm types of color image segmentation
多维特征KFCM聚类分割算法和超像素优化的K均值聚类分割算法均是基于聚类分析思想,图6b所示超像素优化的K均值聚类分割方法首先将岩心图像进行超像素预分割,选定超像素个数为10 000个;然后在分割过程中此两种算法聚类数c均为8,最大迭代次数为100次,聚类结果根据聚类数目分层后,选取相应的颗粒层合并获得最终分割结果。对比图6a、6b可知,K均值聚类分割算法经超像素预分割后仅依赖于颜色特征信息,当背景颜色与颗粒像素点的颜色接近时会被分配至同一个聚类中,存在欠分割现象,颗粒间发生一定程度的粘连,白线框内为一些粘连或欠分割颗粒。而融合纹理、颜色与空间信息的KFCM聚类分割算法增强了颗粒识别的稳定性,分割结果更准确。
如图6c所示,V分量分割算法首先将原始岩心图像转换至HSV颜色空间下,利用亮度信息V分量进行阈值分割,V分量迭代最佳阈值为0.630 69;分割后部分颗粒失真,存在一定孔洞现象,红线框中为一些未能完整识别的岩心颗粒,其原因主要是由于亮度相同而颜色不同的像素点无法正确识别。
综上,在3种算法中,多维特征KFCM聚类分割算法的分割结果最优。
2.3 不同类型岩心颗粒彩色图像的分割效果
图7为2种典型的岩心颗粒显微偏振图像,由于颗粒样本的差异,图像的质量存在差异,特别是颗粒与背景之间的颜色和对比度差别。
图7a、7b分割过程中聚类数c分别为8和6,岩心显微偏振图像转换成灰度图像后,应用Gabor滤波器组从岩心灰度图像提取的纹理特征均值图像如图8所示。

a 岩心原图1b 岩心原图2图7 2种岩心颗粒显微偏振图像Fig.7 Microscopic polarization image of core particles

a Gabor纹理图像1b Gabor纹理图像2图8 岩心颗粒显微偏振图像的Gabor纹理均值图像Fig.8 Gabor texture mean image of microscopic polarization image of core particles
融合从岩心显微偏振图像中提取的颜色、空间坐标以及Gabor纹理特征,进行KFCM均值聚类,然后根据聚类数目分层后选取相应的颗粒层合并,最终分割结果如图9所示。
同理,遵照上述的多维特征KFCM聚类分割算法的过程,图10为从岩心扫描仪中采集的岩心颗粒扫描图像的分割过程,分割过程中聚类数为5。
针对岩心颗粒的显微偏振图像和扫描图像进行多维特征核模糊C均值聚类分割试验,均获得较好的分割结果,能清晰地识别每个岩心颗粒的整体轮廓。 图7a、 7b中大部分岩心颗粒着色均匀,不同颗粒以及颗粒与背景之间的颜色对比度大,颗粒分割效果最好,小粒径颗粒均能被识别。 图10a岩心扫描图像虽然存在噪声影响,岩心颗粒与背景颜色相接近,但也能较好地将颗粒与背景分离。
3 结论与展望
将岩心颗粒彩色图像包含的颜色、空间位置和纹理特征信息融合后进行多维特征KFCM均值聚类分割,能更准确地实现岩心颗粒彩色图像的分割,获得可靠的颗粒粒度分布信息。
多维特征KFCM均值聚类数目和随机的初始化聚类中心的确定方法,对分割结果的稳定性存在一定的影响,这一问题可作为后期进一步研究的方向。

a 分割结果1b 分割结果2图9 岩心颗粒显微偏振图像最终分割结果Fig.9 Final segmentation results of microscopic polarization image of core particles

a 岩心扫描图像b Gabor纹理特征均值图像c 分割结果图10 岩心扫描图像分割过程Fig.10 Segmentation process of core scan images
