页岩有机质纳米孔混合气表面扩散数学模型
2019-11-05王永佩
王永佩
(赤峰盛奥商贸有限公司,内蒙古 赤峰 024000)
非常规油气资源日益重要[1-4]。页岩有机质往往具有疏水性质,一般认为页岩有机质中不含水。对于实际高压页岩气藏,有机质表面大量吸附甲烷[5]。吸附气在浓度梯度影响下发生表面扩散,并且表面扩散量对页岩气总传输量的贡献不可忽略[6]。
研究表明,页岩中黏土矿物与有机质表面均可存在吸附气[7-8]。当页岩基质中孔隙半径小于10 nm时,甲烷吸附显著,甲烷吸附能力随孔隙半径增加而下降[9]。Wentworth[10]通过实验发现实际计量流量大于滑脱流量和克努森扩散模型计算值。跳跃模型中认为[11]:表面扩散的本质是甲烷分子活化后发生解吸附而离开原低能吸附位点跳向另一吸附位点的物理过程。当甲烷分子获得足够能量后,将由吸附态转为游离态。Wu等[5]分析了单组分甲烷气在页岩有机质表面的扩散行为。但该模型不能分析不同气体组分对表面扩散的影响。Song等[12-16]基于孔隙网络模型分析了甲烷气在多尺度页岩基质中的传输规律。但这些模型均考虑页岩气为单一组分甲烷气。在实际页岩气层中,页岩气是以甲烷为主、乙烷和硫化氢等杂质为辅的混合气[17-18]。此外,在页岩气开发过程中往往注入驱替流体以提高最终采收率[19]。因此,不同气体对表面扩散的影响不容忽略[20],必须基于多组分混合气特征,建立适用于混合气的表面扩散数学模型。
笔者基于Langmuir气-固界面系统吸附理论,耦合混合气物性参数计算方法,结合Hwang模型等子模型,建立了考虑混合气特性的页岩有机质混合气表面扩散数学模型。该表面可有效考虑不同气体摩尔分数对页岩气传输性能的影响,对多组分多尺度多传输机理页岩气藏数值模拟技术的发展具有一定基础意义。
1 模型建立
大量研究表明,对于高压页岩气系统,可采用Langmuir气-固界面吸附理论定量表征页岩气吸附量[21-22]。气层压力条件下,页岩气在有机质表面覆盖度可表示为[5-6,23]:

(1)
其中,

(2)
式中:θ为页岩气在有机质表面的覆盖度,无因次;P为页岩气层压力,Pa;PL为Langmuir压力,Pa;PL0为Langmuir压力常数,Pa;ΔH为等量吸附热,J/mol;R为气体常数,J/(mol·K);T为页岩气层的温度,K。
对于混合气,有机质纳米孔混合气吸附浓度可表示为:

(3)
其中,
Mmul=m1M1+m2M2+…+miMi+…+
mi-1Mi-1+mnMn
(4)
dM,mul=m1d1+m2d2+…+midi+…+
mi-1di-1+mndn
(5)
式中:Cs,mul为混合气吸附浓度,kg/m3;Mmul为混合气平均摩尔质量,kg/mol;dM,mul为混合气平均分子直径,m;mi为混合气中组分i占混合气的摩尔质量分数,无因次;Mi为混合气中组分i的摩尔质量,kg/mol;di为混合气中组分i的分子直径,m;NA为阿伏伽德罗常数,mol-1。
依据文献中研究结论,页岩有机质纳米孔表面吸附气发生表面扩散的驱动力是化学势能梯度[24-27]。考虑混合气体效应,页岩有机质表面混合气表面扩散速率可表达为:
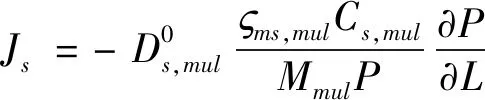
(6)
其中,
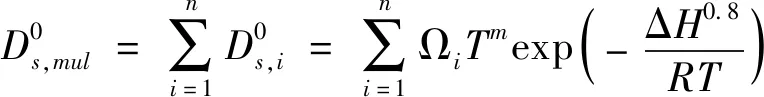
(7)
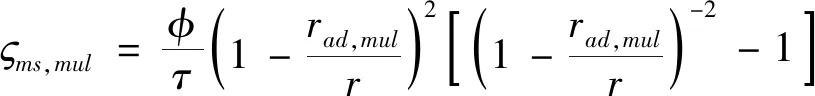
(8)
rad,mul=dM,mulθ
式中,Y为社会总产出;A 代表技术进步水平;L 为劳动力投入;K 为资本投入;参数α和β分别表示资本和劳动力的产出弹性。假设各地区生产函数遵循规模报酬不变的C-D生产函数,即α+β=1。
(9)

2 模型应用
在页岩衰竭开发过程中,页岩气层纳米孔道中压力不断下降。此外,受到应力敏感作用,页岩有机质纳米孔半径随页岩气层压力降低而减小。因此,在页岩气开发过程中,纳米孔道内同时经历压力和水力学流动半径的双重变化。若在开发过程中注入驱替流体(如CO2),为不同纳米孔道内气体组成不断变化。因此,在注气页岩气开发过程中,面临压力、流动半径和气体组成的同时变化。需要利用模型对3个影响因素进行分析。模型运行过程中需要的基本参数如表1所示。模型计算结果如图1~图4所示。模型模拟压力范围0.101~10 MPa,模拟有机质孔道半径为2~30 nm,甲烷摩尔分数为50%~100%。本部分以甲烷和二氧化碳混合气为例展开讨论,这是由于二氧化碳为页岩气藏开发过程中常用工作流体[19]。若读者需要研究其他杂质(如乙烷、丙烷或硫化氢等)对混合气表面扩散特性的影响,将混合气物理参数值代入模型中即可。

表1 模型运行过程中所需物理量数值
不同纳米孔道半径和甲烷摩尔分数条件下混合气压力对吸附层平均厚度的影响如图1所示。由图1可知:(1)随着页岩有机质纳米孔道内混合气压力升高,混合气吸附层平均厚度不断增加。这是由于随着混合气压力升高,有机质表面混合气气体覆盖度升高,导致混合气吸附层平均厚度增加。(2)随着甲烷摩尔分数下降(二氧化碳摩尔分数升高),混合气吸附层平均厚度小幅下降。这是由于甲烷分子直径约为0.38 nm,而二氧化碳分子直径约为0.33 nm。二氧化碳摩尔分数升高导致混合气平均分子直径减小。由于模型基于Langmuir单层吸附理论,因此混合气平均分子直径下降导致混合气吸附层平均厚度减小。(3)纳米孔道半径对混合气吸附层平均厚度的影响可以忽略。
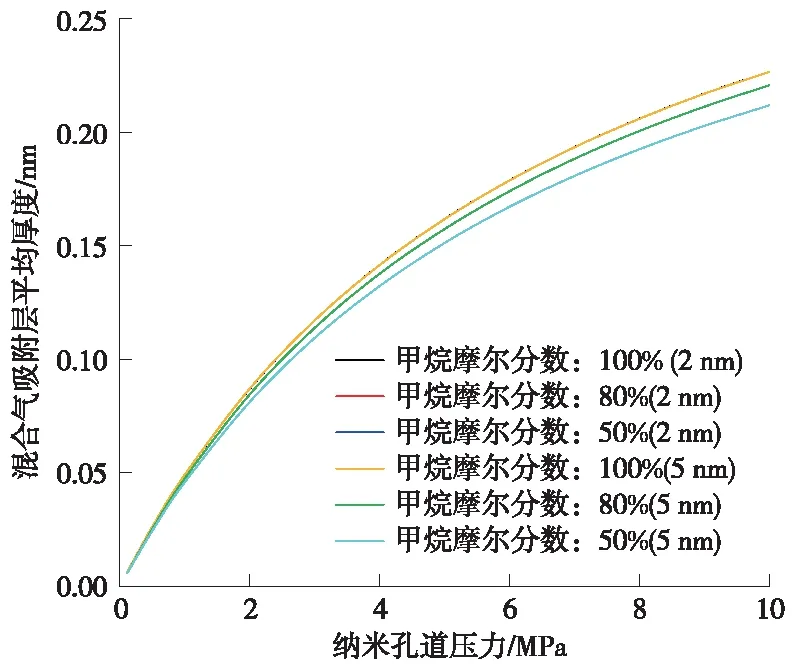
图1 不同纳米孔道半径和甲烷摩尔分数条件下混合气压力对吸附层平均厚度的影响Fig.1 Effect of pressure on average thickness of absorption layer under different radii and methane content conditions
不同纳米孔道半径和甲烷摩尔分数条件下混合气压力对混合气吸附质量浓度的影响如图2所示。由图2可知:(1)随着页岩有机质纳米孔道内混合气压力升高,混合气吸附质量浓度不断增加。这是由于随着混合气压力升高,有机质表面混合气气体覆盖度升高,导致页岩有机质表面甲烷和二氧化碳浓度升高。甲烷和二氧化碳在物理化学特征上存在更深层次的差异,因此在甘洛根等有机质表面的吸附往往具有竞争吸附特征[30]。甲烷/二氧化碳与不同成熟度的甘洛根组成的系统的吸附特征也不尽相同[31]。目前,国际上常常采用分子模拟方法耦合甲烷分子和二氧化碳分子的众多精确物理性质进行纳米级别流动模拟。该方法具有很高的精确性,但更加适合于机理分析,由于计算量巨大,对于页岩气藏大规模注气开发或压力衰竭开发不太实用。(2)甲烷与二氧化碳组成的混合气的吸附质量浓度随二氧化碳摩尔质量分数升高而增大。这是由于二氧化碳摩尔分子质量(0.044 01 kg/mol)大于甲烷摩尔分子质量(0.016 kg/mol)。因此,单位摩尔吸附气体质量增加,吸附质量浓度增加。(3)纳米孔道半径对混合气吸附层浓度的影响可以忽略。这是由于该模型基于Langmuir单层吸附理论建立。因此有机质单位表面积吸附分子摩尔量与孔隙半径不具备明显函数关系。但目前国际上已有文献报道了页岩气多层吸附现象[32-36]。笔者在后续工作中将逐步开展多层混合气吸附建模研究。

图2 不同纳米孔道半径和甲烷摩尔分数条件下混合气压力对混合气吸附质量浓度的影响Fig.2 Effelt of pressure on absorption concentration under different radii and methane content conditions
不同纳米孔道半径和甲烷摩尔分数条件下混合气压力对混合气表面扩散速度的影响如图3所示。由图3可知:(1)随着页岩有机质纳米孔道内混合气压力升高,混合气表面扩散速度不断增加。这是由于随着混合气压力升高,有机质表面混合气气体覆盖度升高,吸附气摩尔浓度增加,摩尔表面扩散速度增加。(2)随着二氧化碳摩尔分数增加,混合气表面扩散摩尔速度增加。(3)当纳米孔道半径由2 nm增加至5 nm时,混合气吸附层平均厚度和混合气吸附层浓度均变化很小,但表面扩散摩尔速度迅速降低。这是由于方程(6)中表面扩散修正系数随纳米孔道半径增加而迅速下降,导致表面扩散摩尔质量下降。

图3 不同纳米孔道半径和甲烷摩尔分数条件下混合气压力对混合气表面扩散速度的影响Fig.3 Effect of pressure on surface diffusion velocity of gas mixture under different radii and methane content conditions
不同混合气压力条件下纳米孔道半径对表面扩散修正系数(ςms,mul)的影响如图4所示。

图4 不同混合气压力条件下纳米孔道半径对表面扩散修正系数(ςms,mul)的影响Fig.4 Effect of radii of nanopore on surface diffusion correction (ςms,mul) under different pressure conditions
由图4可知,混合气表面扩散修正系数(ςms,mul)随纳米孔道半径增加而迅速下降。当纳米孔道半径足够大时,存在半径临界值。即孔道半径大于临界值,则孔道半径对混合气表面扩散修正系数影响迅速减弱。该临界值是混合气压力的函数。混合气压力升高,临界值增大。
3 结论
(1)随着二氧化碳摩尔分数升高,混合气吸附层平均厚度小幅下降。这是由于甲烷分子直径约为0.38 nm,而二氧化碳分子直径约为0.33 nm。由于模型基于Langmuir单层吸附理论,因此混合气平均分子直径下降导致混合气吸附层平均厚度减小。
(2)甲烷与二氧化碳组成的混合气的吸附质量浓度随二氧化碳摩尔质量升高而增大。这是由于二氧化碳摩尔质量(0.044 01 kg/mol)大于甲烷摩尔质量(0.016 kg/mol)。因此,单位摩尔吸附气体质量增加,吸附质量浓度增加。
(3)混合气表面扩散修正系数(ςms,mul)随纳米孔道半径增加而迅速下降。当纳米孔道半径足够大时,存在半径临界值。即孔道半径大于临界值,则孔道半径对混合气表面扩散修正系数影响迅速减弱。该临界值是混合气压力的函数。混合气压力升高,临界值增大。
