一种基于松弛算法改进的最小组播树生成方法
2019-11-05向雄李羡童
向雄,李羡童
(广州大学华软软件学院网络技术系,广州510990)
0 引言
构建代价最小的组播树是计算机网络领域一个经典的问题,组播树问题一般化就成了斯坦纳树(Steiner Tree,ST)问题[1]。假设R 是图G 的顶点子集,则ST 就是一个连通R 中所有顶点且代价最小的子图。这类问题应用价值非常广泛,例如网络层RP 组播和单源组播、应用层的P2P 组播等。组播技术常见于流媒体、文件传输以及订阅/发布的消息模型等各种网络应用,如视音频会议、网络直播、点播、多人游戏程序等。近年来随着VLSI 的发展,ST 算法被用来优化集成电路设计,应用范围延伸到了芯片设计领域。
研究表明,ST 是一个NP 难问题[2],其确定性算法都具有指数级的时间复杂度。因此在应用性研究方面重点聚焦在寻找多项式时间内近似算法或者解决某些特殊情形,文献[3]对各类确定性算法和启发式算法进行了全面的分析和比较。
随着NFV 及5G 等技术的发展,近年来网络有向SDN 新型网络演进的趋势[4]。相比传统路由器中的嵌入式控制系统,SDN 中执行算法的控制器部署在高性能的服务器集群上,并且可以利用全局信息对网络进行精确地编排,高性能的传输算法对充分利用网络基础设施的作用非常巨大。
为此,本文对组播传输算法展开了研究,提出了一种在松弛算法基础上进行环破除的组播树生成方式,后面简称RR(Relax based Ring)算法。该方法在利用松弛算法生成传播树的同时发现可优化环,然后破除这些可优化环即可得到代价更小的传播树。本文用到的符号及定义如下,参见图1,其中加粗的线条表示传播路径。
G:无向带权连通图。G=(V,E)是一个包含n 个顶点的图,V 是G 中的顶点集,E 是G 中的边集,E={(u,v)|u,v∈V}。
s:组播源,s∈V。
F(u,v):表示两节点之间的传输代价,当u,v 相邻时它就边(u,v)上的权值,当u,v 不相邻时表示从u 沿着组播树到达v 时所经过的边的代价和,
R:组播的接收者集合,R⊆V。R 中的节点称为R节点
P(u,v):表示树中两顶点u,v 之间路径,是从u 沿树到达v 所经过的边集。
W(u):表示以u 为树根的子树上所有边的代价和。
T:G 中的子树,T=(VT,ET),T⊆G,VT⊆V,ET⊆E。
RR 问题与ST 问题目标一致,可描述为:构造以s为根的树,使得R ⊆VT且W(s)最小。
本文结构:先介绍相关研究,然后介绍松弛算法及其过程,随后对可优化环进行定义并论证其存在性和优化性,分析可优化环之间的关系及破除顺序,最后给出算法的运行效果,得出结论。
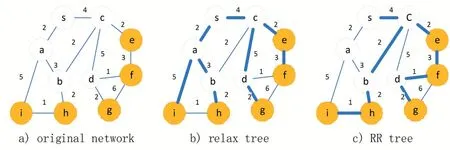
图1 RR树示例
1 相关研究
目前与此相关的研究成果主要有KMB、SPH、ADH及LMC 等算法。KMB[5]是一种经典的组播树生成算法,它首先使用Prim 或Kruskal 算法从图G 中找出由组播节点所形成的子图的最小生成树(MST),然后将此MST 代回到图G 中,剪除掉无关路径就得到了一棵组播树,时间复杂度为O(mn2)。SPH(Shortest Path Heuristic)[6]算法也称作MPH(Minimum Path Heuristic),它首先将源点添加到组播树,然后依次将与树最近的节点添加到树中,直到所有组播节点均已加入,复杂度同KMB。ADH(Average Distance Heuristic)[7]算法则选择一个节点作为中心节点,然后以它为中心生成|S|+|R|棵子树,再用最短路径依次将这些子树连接起来得到最终的组播树,时间复杂度为O(n3)。SPH 和ADH 都宣称在性能上略优于KMB。还有一种朴素组播路由算法[8]宣称其性能超越了KMB,这是一种基于权重的贪婪算法。当一个新节点加入到组播树时,它会选择一条到树中最短的链路进行连接。LMC[9]算法采用类似于Dijkstra 算法来寻找源到其他节点的最短路径,当遍历到一个R 节点时,LMC 会将它的dist 值置0。当所有R 节点都被包含进组播树时算法结束。其他的与最小代价树有关的算法还有扩展的Dijkstra 算法[10]、Bellman-Ford 算法及SPFA 算法[11]等。SPFA 算法并没有给出正确的严格证明,它在Bellman-Ford 算法基础上添加了队列功能,各节点可以循环入队,队列为空时结束算法,这样可以减少组播总代价,但在极端情形下有可能陷入死循环。
近年来,有人尝试利用智能算法和机器学习等技术来研究ST 问题[12-14]。文献[13]利用基于蚁群的并行算法在GPU 上取得了比KMB 算法代价优化8%运行速度快2 倍的效果。文献[14]在解决直线斯坦纳最小树问题时利用KNN 算法来缩小解空间,提升了解的质量,主要应用于芯片领域。文献[15]提出一种免疫算法把每个steiner 点看作疫苗,然后不断地把它“接种”到最小生成树上,多次迭代后可以达到99.95%的最优路径。这类算法的共同点是应用于专门的领域,对设备有特殊的要求。
当前算法都是近似算法,都无法达到最优,在生成树代价方面还存在进一步降低的空间。数据模拟表明,在减小总代价方面,RR 算法能达到和超越之前的最优水平。
2 松弛算法
定义一松弛算法。对于每个顶点v∈V,都设置一个属性dist(v),表示从源点S 到v 的最短路径上权值的上界,初值设置为无穷大。算法的执行过程是不停地寻找dist 值最小的顶点u,然后访问u,访问时遍历u的每一个邻居j,如果满足松弛条件p,则执行松弛过程q,并将j 的父节点标记为u,记作π(j)=u。。
松弛算法是基于连通图的,所以源到所有R 节点都有路径可达,初始状态下当s 与目标节点没有直接连接就当作是一条权值无穷大的边,然后不断地试图把这条边拆开,用通过其他节点中转的代价更小的边集来替换,这样两点之间一条边就变成了多条边,变得“松弛”了。
Dijkstra 及扩展的Dijkstra、LMC 等都属于松弛算法,其松弛条件p 均为:dist[j]>dist[u]+F(u,j),只是松弛过程q 不一样。利用Dijkstra 松弛算法可以得到如图1(b)中加粗线条所示的松弛树,使用环破除方法可以进一步降低其总代价。
3 可优化环
定义二可优化环路。对节点a 的邻居b 进行松弛操作时,记a,b 共同的最邻近祖先节点为n,如果满足条件:①b 已经被访问过;②F(a,b)≥F(n,b)-F(n,a);③max{F(n,a),F(n,b)}>F(a,b),则边(a,b)与路径P(n,a)和P(n,b)所构成的环路是一个可优化环路,记作环(a,b)。n 是环(a,b)的分支节点,a 是环的起点,b 是环终点。

图2 可优化环
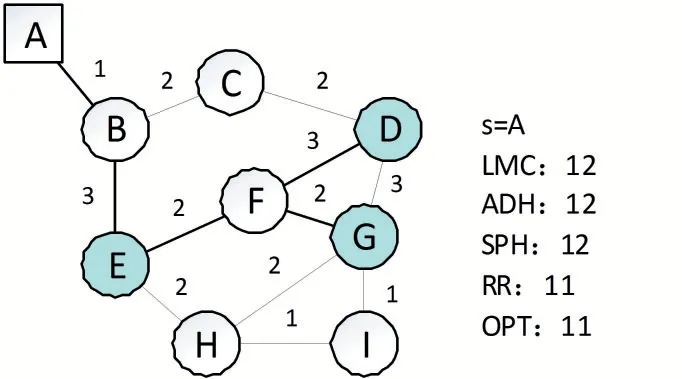
例如在图2(a)中,dist(n)=8,dist(a)=12,dist(b)=15,则F(n,a)=dist(a)-dist(n)=4,F(n,b)=dist(b)-dist(n)=7,因为F(n,b)-F(n,a)=7-4=3 定义二中的条件2 若不满足,则根据定义一,它就满足了松弛条件,那么a 就成为b 在组播树上的父节点,这种情形是不用优化的,因为此时以n 为根的子树代价已经是最小的了。 定义二中条件3 的作用是过滤掉一些无法优化的环。max{F(n,a),F(n,b)}>F(a,b)不满足,那就意味着F(a,b)会大于或等于P(n,a)和P(n,b)路径上任何一条边的权值,这样一来不管哪条边被边(a,b)替换,只可能增加树的总代价,再进行优化是没有意义的。 RR 算法中的核心思想就是找出松弛树中的可优化环进行破除,破除时只需简单地去掉环中的最大边。我们知道,去掉环路中的一条边并不会影响图的连通性,这样就可达到降低组播树总代价的目标。 定理一去掉可优化环中的最大边可以降低树的代价。 定义三中转节点:如果一个可优化环上某节点不是R 节点,并且它除了环中的两条边之外其余的边都不在任何树中,也不在其他可优化环上,则应把这两条边合并为一条边,这个节点叫中转节点。如图2(b)中的节点a。 定理二环破除之前先聚合中转节点更能降低代价。 证明:中转节点只是一种中间转发节点,既不是分叉点,也不是目标节点,聚合它之后可以得到代价值更大的边,从而增加在进行环优化时被去掉的可能性,如果被去掉了,则降低的代价值更大,从而得到的组播树总代价更小。 例如在图2(b)所示的以s 为分支节点的环(b,c)中,a 是一个中转节点,聚合之前环路中最大边为F(s,c)=4,环优化结果为W(s)=7。聚合中转节点a 后,sab被看作是一条边,那么最大边为F(s,b)=5,聚合中转节点后的再进行环优化结果为W(s)=6。破环前的父子关系为{π(b)=a,π(a)=s,π(c)=s},破环后节点a 被合并路径P(s,b)被视作一条权重为5 的边去掉了,增加了(b,c)边,则节点间父子关系修改为{π(b)=c,π(c)=s}。 RR 算法主要过程是生成松弛树的同时生成可优化环,然后按序逐个破除可优化环。具体算法如下: 输入:图G,起点s Case1.G=,此时G内幂零,由定理5可知若m≥2,P∗(G)连通且diam(P∗(G))≤4;若m=1,由定理6的证明可知CP(Q)=1,再利用定理5可知真幂图P∗(G)不连通且连 输出:多播树T 一、初始化数组T、dist、opened;初始化栈cq;dist[s]=0;opened←{s}。 二、while opened≠Φ do: (1)i=pop(opened,0);T←{i} (2)遍历i 的每一个邻居节点j: ①若满足松弛条件,则:dist[j]=dist[i]+F(i,j),π(j)=i;open←{j};opened 升序重排;continue; ②若j 已访问过,则进一步判断环(i,j)是否满足定义二条件,若是则cq←{(i,j)}; 三、while cq≠Φ do:(1)取出栈顶环(i,j); (2)对节点i,j 进行父节点回溯,找到环(i,j)的分支节点n; (3)合并Path(i,n)和Path(j,n)上的中转节点。 (4)去掉Path(i,n)∪Path(j,n)∪(i,j)中的最大边;修改相关节点的父子关系; 四、for node in T:#剪除末端非R 节点的分支,末端节点度为1 1.if degree(node)=1 and node 不是R 节点: ①从node 上溯父节点,删除度为2 的父节点,直到父节点度大于2 算法的第二步首先验证松弛条件,若成立则加入松弛树,否则验证可优化环条件,如果是则将其入栈。第三步的执行过程如图3 所示。开始时cq 栈中有四个环,在步骤a)中,从cq 栈顶取出环(g,f),破环的结果是删除边(g,f),无需对路径作任何更改。在步骤b)中,从栈顶取出边(d,f),环优化的结果是删除边(c,d)。得到c)所示的图。在步骤d)中需要破除的环(b,c),此时节点a 点为中转节点,于是合并sa 和ab 为一条边,记为sab,它就成了环(b,c)上要被去掉的最大边,这样就得到了步骤f)所示的最终结果 图3 Dijkstra树的环破除过程 RR 算法第三步中的2、4 小步分别进行父节点回溯和环破除过程,下面分别说明之。 (1)父节点回溯 父节点回溯的目的是为了找到环(i,j)的分支节点,首先上溯到i,j 的共同最终祖先节点s,也就是组播源,分别得到各自的父节点列表iparents 和jparents,然后将两个列表倒序排列,那么两个列表中前k 个相同元素就是i 和j 节点所在的公共分枝,公共分枝的最后一个节点环(i,j)的分支节点。主要Python 实现代码如下。 temp=i while g.node[temp]!=s: temp=g.node[temp][parent] iparents.append(temp) temp=j while g.node[temp]!=s: temp=g.node[temp][parent] iparents.append(temp) iparents.reverse();jparents.reverse() for m,n in zip(iparents,jparents): if m!=n:return iparents[iparents.index(m)-1] (2)环破除过程 环破除的主要过程是去掉环路中的最大边,将最大边的子节点及其以下的子节点反向连接。主要Python 实现代码如下。其中Circle 函数返回环中边集,每一条边的表示形式为元组(u,v,w),u 是v 在树中的父节点,w 为权重。为避免冗长说明,本处省略了中转节点合并过程。 def BreakCircle(i,j,n): edgelist=Circle(i,j) edge=max(edglist,key=lambda d:d[2])#找到权值最大边 index=edgelist.index(edge) while True: child=edge[1] if child==j:#如果最大边的终边为环终点j,则j 父节点设为i g.node[j][parent]=i;break elif child==i:#如果最大边的终边为环起点i,则i 父节点设为j g.node[i][parent]=j;break else:#否则一直下溯,将下一条边的起点变成上一条边终点的父节点 next_edge=edgelist[index+1] g.node[child][parent]=next_edge[0] index=index+1 g.edges.remove(edge) edge=next_edge 假设问题的规模(即G 中的顶点数)为N。算法的第二步共需要循环N 次,因为每个节点都会进入到opened 表一次。循环内部需要将opened 重新排序。采用Python 实现时,其列表对象的sort 方法默认是采用Timsort[16]排序算法,它结合了合并排序和插入排序的特点,能充分利用已经排好序的数据特点,是一种非常高效的算法。Timsort 算法的时间复杂度在最坏的情形下(例如随机序列)为O(log(n!)),最好情形下不超过O(n)。opened 表中元素是依次加入的,每次排序时大部分元素都处于有序状态,正好符合Timsort 算法的最佳情形。在循环内部遍历节点的k 个邻居,访问每个邻居时需要m 个操作,故其时间复杂度为N*N*k*m,由于m 和k 都是与规模无关的常数故们可以估算得出第二步的时间复杂度不超过O(N2)。 算法第三步while 循环内部的主要工作是寻找环的分支节点破环。最坏的情况为分支节点为s,i,j 回溯时两条路径不相交地走完了图中所有节点。假设i所在的路径上节点数为k,则j 所在的路径节点为Nk-3,故其寻找共同父节点的时间复杂度为k*(N-k-3)。破环时要比较(N-1)次边大小,如果要进行中转节点合并,则可以减少比较操作,但增加了求和操作,所以比较或求和的总次数还是(N-1)次,可算得操作次数为k*(N-k-3)+(N-1)≈k*(N-k)+N,当k=N/2 时值达到最大,为N2/2+N,时间复杂度量级为O(N2)。最好的情况。i、j 的共同父节点就是它们各自的直接上级节点。此时环路中只有三条边,只需3 次比较即可完成。由此可见,即使是最坏情况,其时间复杂度量级也不会超过Ο(N2)。因此第三步时间复杂度为O(N2*M),其中M 为环的个数。下面分析M 的取值可能范围。 假设G 是一个随机网络,其中每条边的代价值量化到1~10 十个等级,则∀(u,v)∈E,Cost(u,v)是一个随机变量,记作X,其概率分布为: X 的概率母函数为: 在图2 所示的可优化环中,Path(n,a)和Path(n,b)中边数分别记为Na和Nb,Na和Nb两个独立同分布的随机变量,很明显它们符合泊松分布特点,其概率母函数G(s)为: 令Ya=Cos(tn,a),则Ya=也是随机变量,根据(2)和(3),由数学性质可得Ya的概率母函数H(s)为: 由式(4)即可计算出Ya和Yb的概率分布。 由定义二可知,在分支节点为n 的可优化环(a,b)中,当采用Dijkstra 松弛条件时,必然有Cost(a,b)+Cost(n,b) p = P{Cost(a,b) 亦即: 若图G 节点的平均度为K,那么总的边数为NK,去掉传播树中的N 条边,于是可得出可优化环的数量M=N(K-1)p。 第四步剪除多余分枝过程很明显时间复杂度不超过O(N2)。 综合以上步骤可得RR 算法的时间复杂度上界为2O(N2)+Ο(N2*M)~O(N2*M)。 实验时使用的网络由Python 中的networkx 库函数random_kernel_graph 随机生成,调用方式为nx.random_kernel_graph(n,lambda u,w,z: d *(z- w),lambda u,w,r:r/d+w),其中n 和d 分别要生成的网络的节点数和平均度,每条边的权重为1-10 之间的随机数。 我们比较了不同松弛算法的对组播树的影响,见表1。最大长度是指组播树上最远两个节点之间的边的数目,这也是衡量组播算法的一个标准,越小意味着组播延迟越低。从表中可以看出,在总代价方面,采用LMC 的RR 算法效果明显优于采用Dijkstra 的RR 算法,但在最大长度方面却不如后者。其中可能的原因是LMC 本身在降低代价方面优于Dijkstra。 表1 LMC 和Dijkstra 两种松弛过程对RR 算法的影响 我们分析了图4 所示的网络中各种算法所得的总代价,其中OPT 是用穷举法找到的最佳路径,可以发现RR 是最能接近OPT 的算法。 图4 RR算法与其他算法在特定图上运行结果对比 ST 问题是一个基础性的课题,其应用范围非常广泛,对它进行研究也是一种很有启发性的工作。近年来随着人工智能技术的发展,有人提出一种观点认为数据的重要性大于算法,特别是在神经网络领域,认为只要有了大量的带标注或不带标注的数据,就可以通过监督学习或非监督学习训练出一个模型来解决相关问题。但ST 问题目前很难用机器学习方式解决,因为ST 问题的规模的状态是不断变化的,没有内在规律,也就是说不存在某个隐藏在数据背后的函数来将问题映射到结果,很难用一个模型表达出来。对传统算法的研究与改进,既有助于促进机器学习技术的发展,也能提高现有应用的效率和水平。4 算法过程

5 时间复杂度分析
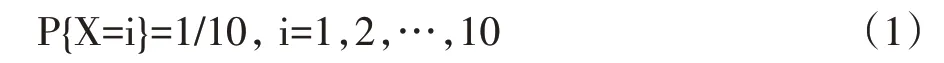

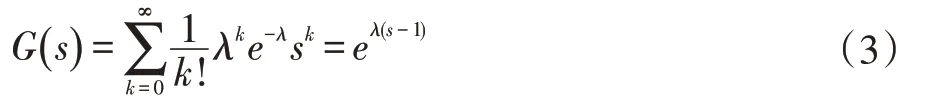


6 实验与比较

7 结语
