钢桁腹-混凝土组合箱梁偏载系数取值影响因素分析

于小芹，杨霞林

(兰州交通大学, 甘肃 兰州 730070)

作为新兴的钢-混组合结构，钢桁腹-混凝土组合箱梁中的钢桁腹杆取代了普通混凝土箱梁中的混凝土腹板。该组合箱梁由混凝土顶底板和连接顶底板的钢桁腹杆构成，外加体内、外预应力钢束，使钢与混凝土完美结合，高效率工作[1]。其基本构造如图1所示。

钢桁腹-混凝土组合箱梁桥自重小、受力简单、外观优美、通风性能好等优点均优于其他箱梁。钢桁腹杆便于采用工厂化大批量生产，而且该组合箱梁应用了体外预应力等新技术，便于张拉、检测、维护和更换。因此，在中等跨径与大跨径桥梁中，该结构的竞争优势颇为良好[2]。

国外对该组合结构的研究主要集中于节点与全桥承载能力两个方面，主要方法是先对节点或整体结构的受力性能进行实验研究，再通过有限元的数值模拟对试验数据进行验证[3-5]。而我国学术界对该组合结构的研究正处于初步阶段，主要借助有限元软件对该组合结构进行研究[6-7]，理论公式推导与工程实例均较少[8]。

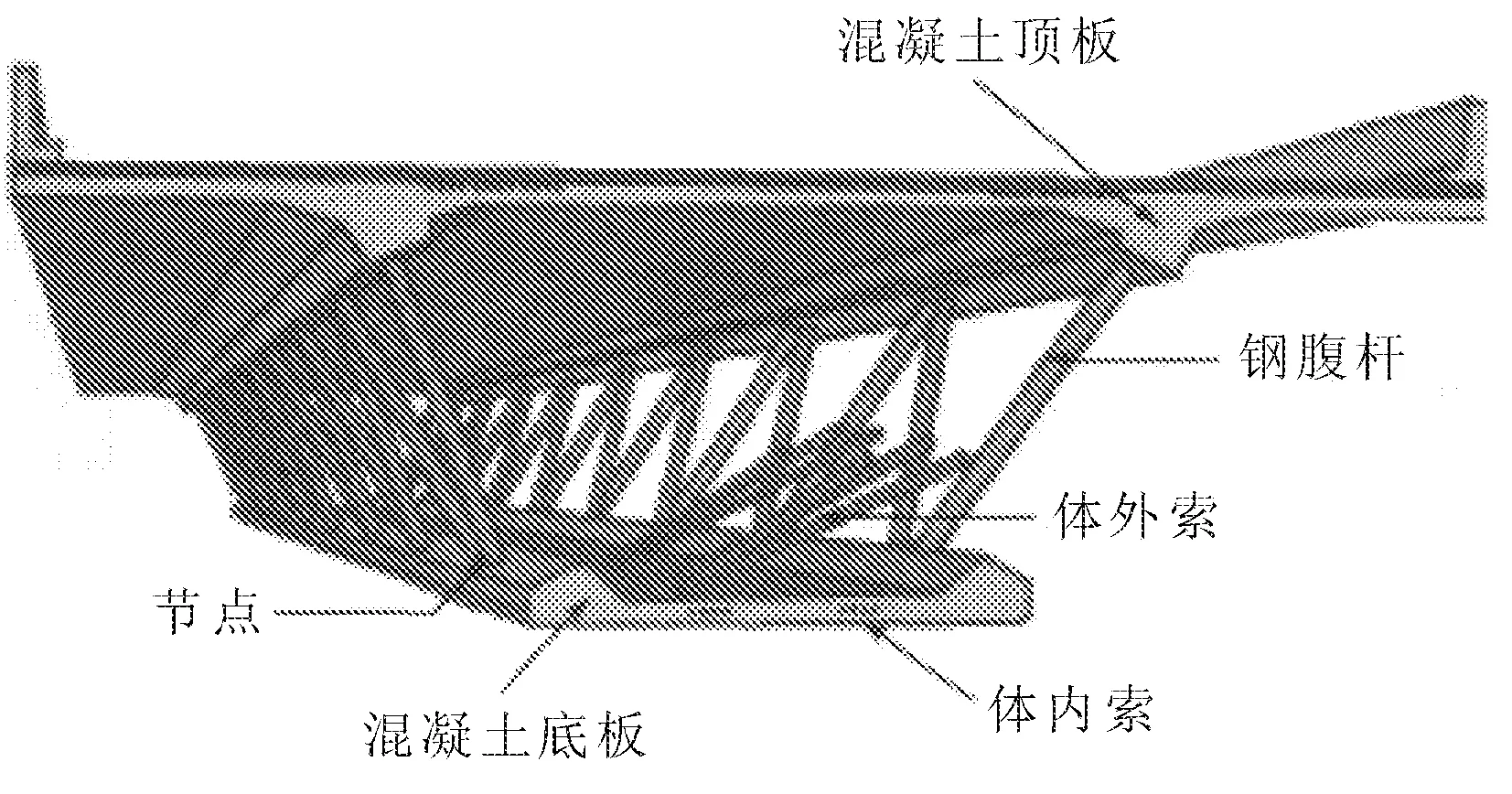
图1 钢桁腹-混凝土组合箱梁构造

偏载系数在国内规范中没有明确定义与限定，有关偏载系数公式算法还不够精确，现在一些比较常用的计算方法有经验系数法、偏心压力法和修正的偏心压力法等[9]。经验系数法一般将经验系数ξ1取为1.15，这样取值比较简单方便，但是没有考虑箱梁的尺寸变化、荷载大小和偏心距等因素，对一些桥型来说偏于不安全；偏心压力法和修正的偏心压力法都有特定公式求偏载系数，后者是在前者计算上又考虑了抗扭刚度[10]。现在工程上又出现了一种荷载增大系数法，为了得到所要求的设计内力，将增大系数中的最大值与车辆轴荷相乘所得到的值输入到ζmax程序中，即可得到所求结果。该方法较为简便且偏于安全，更适用于工程使用[11]。

国内外对钢桁腹-混凝土组合结构偏载系数的分析较为罕见，是否直接利用现有计算理论及经验系数法尚待进一步研究和探讨，本文将利用有限元软件ANSYS对钢桁腹-混凝土组合箱梁影响偏载系数的主要参数进行敏感性分析，得到偏载系数随腹杆壁厚、悬翼比、高跨比以及宽跨比变化的变化规律，望能为实桥设计提供参考。

1 有限元模型

1.1 ANSYS建模

本文讨论的简支钢桁腹-混凝土组合箱梁的有限元模型横向和纵向尺寸构造见图2和图3。选用Solid 185来进行顶板和底板的模拟，选用Beam 188进行钢桁腹杆的模拟，钢桁腹杆与混凝土顶底板进行刚接形成共节点形式[12]，模型的相关数据资料在表1中显示，有限元模型如图4所示。腹杆倾斜的角度为67°左右，两相邻腹杆的最大距离为1.95 m。

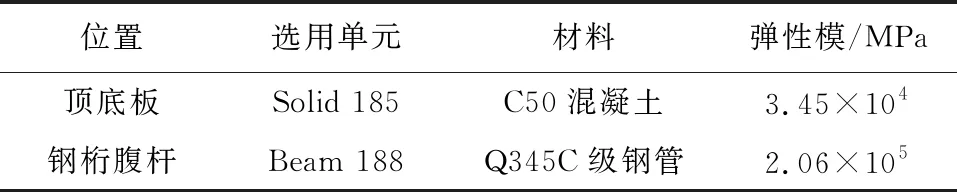
表1 有限元模型的相关参数

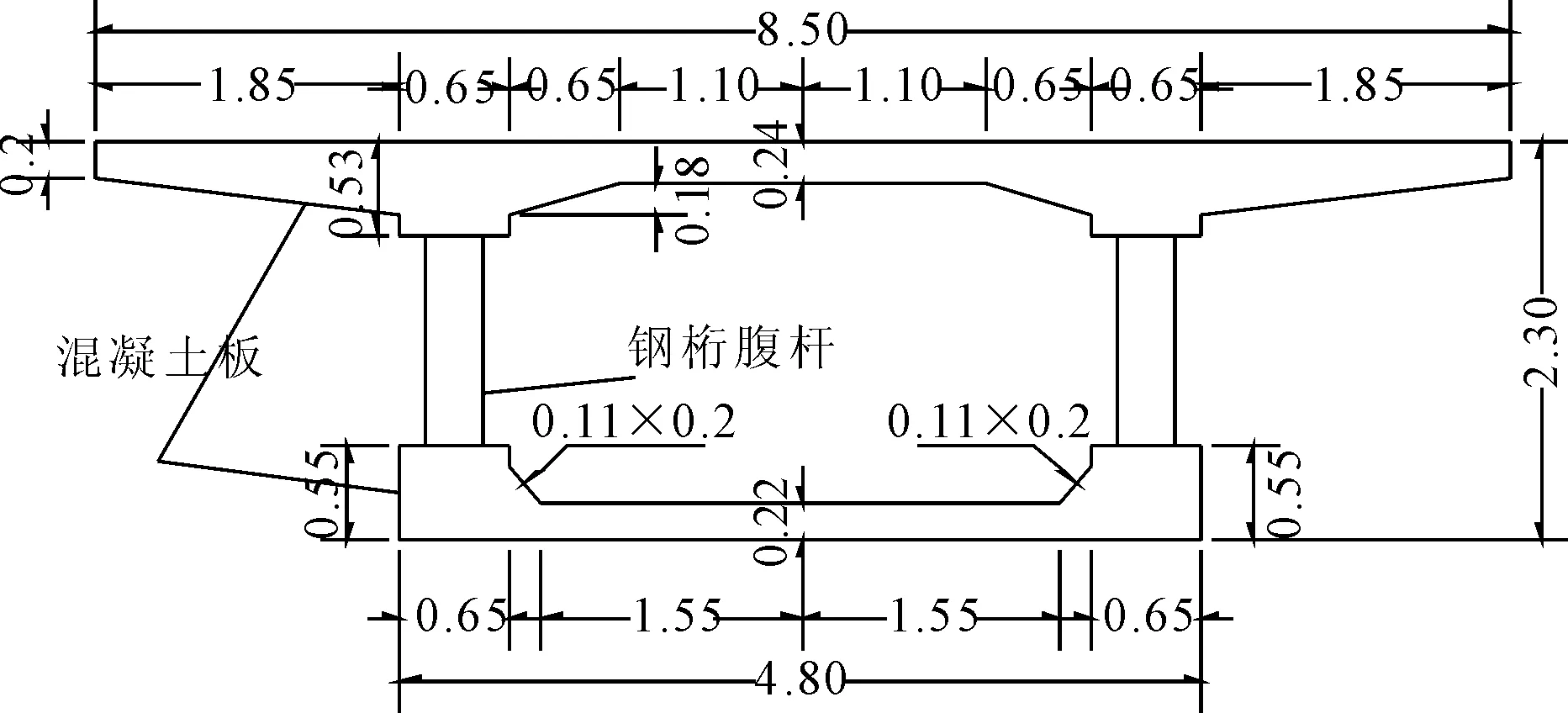
图2 组合结构横截面尺寸图示(单位：m)

图3 组合结构纵向尺寸图示(单位：m)

图4 有限元模型图示

1.2 组合箱梁加载点与分析点

将偏载系数用应力和位移这两种不同的方式划成(正)应力增大系数(指在偏心荷载作用下，控制截面即腹板处的最大应力与平均应力的比值)和位移增大系数(指在偏心荷载作用下，控制截面即腹板处的最大位移与平均位移的比值)，分别用ξ1和ξ2表示。文献[11]提出此方法仅适用于跨中，不适用于支座处，因此，仅在跨中处施加荷载进行讨论。依据《公路桥规》中车道荷载的要求对有限元模型施加P=330 kN的跨中集中偏载[13]，桥梁自重均匀分布，对偏载增大系数产生影响较小，计算中可忽略。跨中集中偏载的施加位置在图6中的3点处，取1点与2点的应力值与挠度值研究钢桁腹-混凝土组合箱梁桥的ξ1和ξ2变化规律。

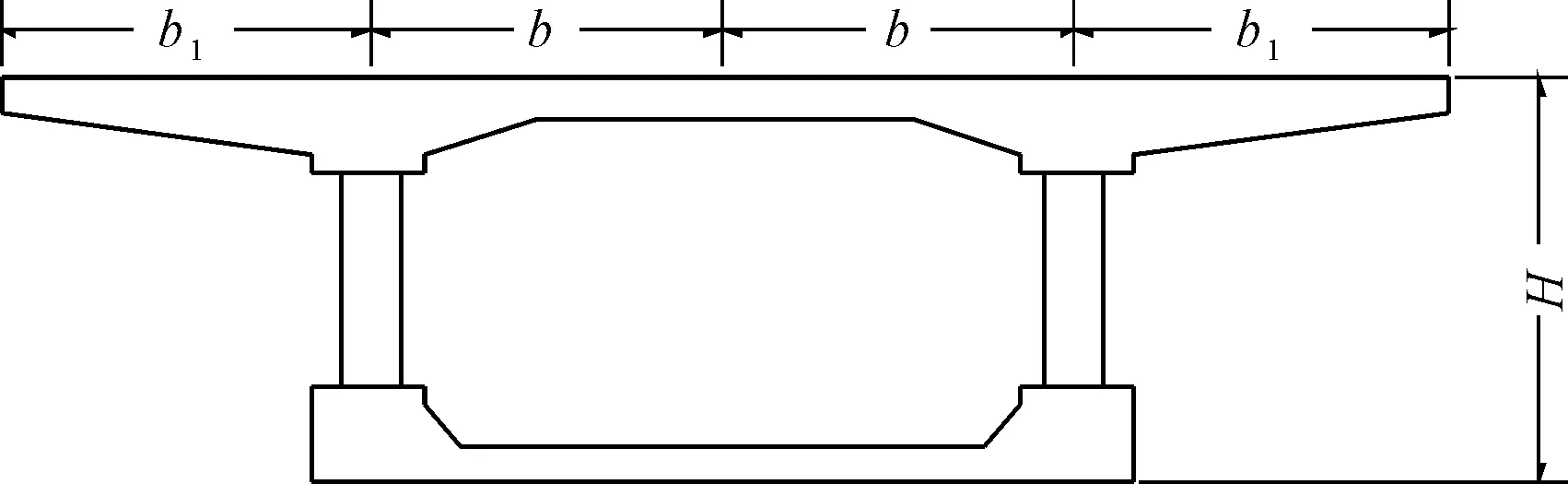
图5 钢桁腹-混凝土组合箱梁模型尺寸

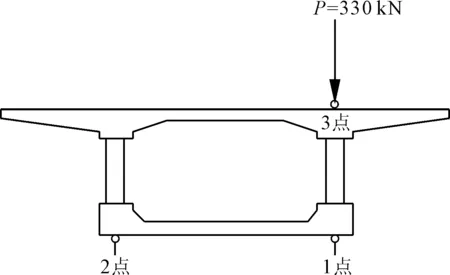
图6 跨中集中偏载施加点与讨论点图示

为方便计算，将ξ1和ξ2按各自的定义分别简化为式(1)和式(2)：

(1)

(2)

式中:σz1和σz2分别是偏载P作用下1点和2点的纵向应力，Uy1和Uy2分别表示在偏心荷载P作用下1点和2点的竖向位移。

2 几何参数分析

2.1 腹杆壁厚

腹杆壁厚是指腹杆截面外圆半径R0与内圆半径Ri之差，腹杆截面如图7所示。

取R1=10 cm，R0=15 cm、20 cm、25 cm、30 cm、35 cm、40cm。其余尺寸不变，共建立6个有限元模型。分析数据可见表2和图8。

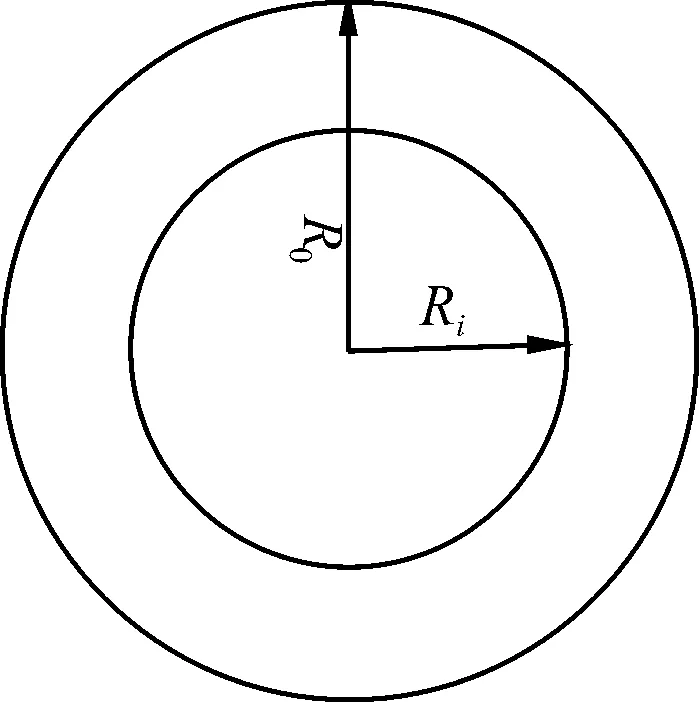
图7 腹杆截面

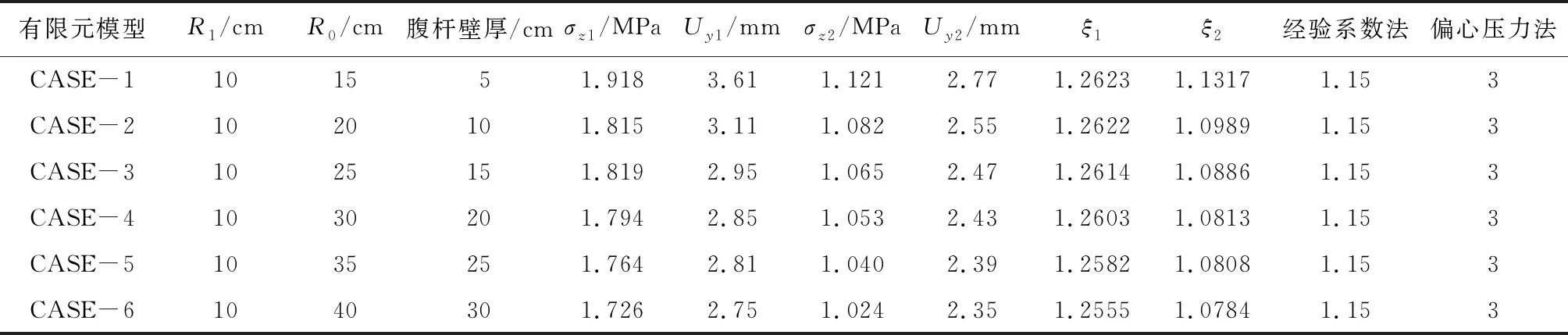
表2 腹杆壁厚对ξ1和ξ2的影响

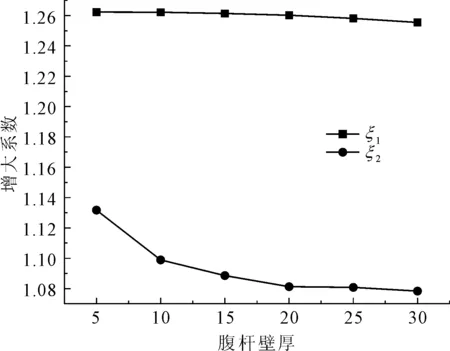
图8 腹杆壁厚对ξ1和ξ2的影响

由表2和图8能够看出，腹杆壁厚越大，ξ1和ξ2越小，ξ1的减小幅度较小，整体下降幅度也不明显，最大值不超过1.3，最小值也在1.25以上，变化不大。而ξ2在截面半径差从5 cm变为15 cm时，变化幅度相对较大，而从腹杆壁厚为15 cm以后时，ξ2减小幅度变小。从整体来看，ξ1比1.15大，而ξ2均比1.15小，可见，经验系数法取值在腹杆截面面积变化的影响来讲，相对于ξ2偏于安全，而相对于ξ1偏于不安全。偏载系数的变化曲线说明偏载系数能够受到腹杆壁厚变化的影响，但敏感度较低。现实计算中，采用应力和位移进行腹杆截面面积变化时偏载系数的计算时会呈现出些许差异，对此应当注意。

2.2 悬翼比

悬翼比是b1/b，如图9所示。为满足工程实用性，现取b=2.4 m，将悬翼比从0.5以0.1逐次递增至1.0，则b1分别为1.20 m、1.44 m、1.68 m、1.92 m、2.16 m、2.40 m。其余尺寸不变，共建立6个有限元模型，分析悬翼比对位移放大系数与应力放大系数的影响，得到相应的变化曲线，结果见图9。

由图9可知，悬翼比在0.5到1.0范围内的变化对ξ1和ξ2均较小，尤其对ξ1几乎没有影响，而ξ2随悬翼比的增大而增大，但增大幅度很小。ξ1和ξ2均比经验系数值1.15大，用经验系数法取值相对于ξ1和ξ2均偏于不安全。偏载系数的变化曲线说明偏载系数受悬翼比变化影响很小，必要时可以忽略其影响。

从上述分析可见，国内外名物化研究的重点既有相似之处，又有很大差异。相似点在于热点都涉及语法隐喻、翻译、认知、语言类型等，差异较大的有两点，一是国内比较关注名物化现象的词法研究，而国外更关注句法；二是国内的名物化研究还是以理论研究为重，而国外已经出现明显的实证研究转向。

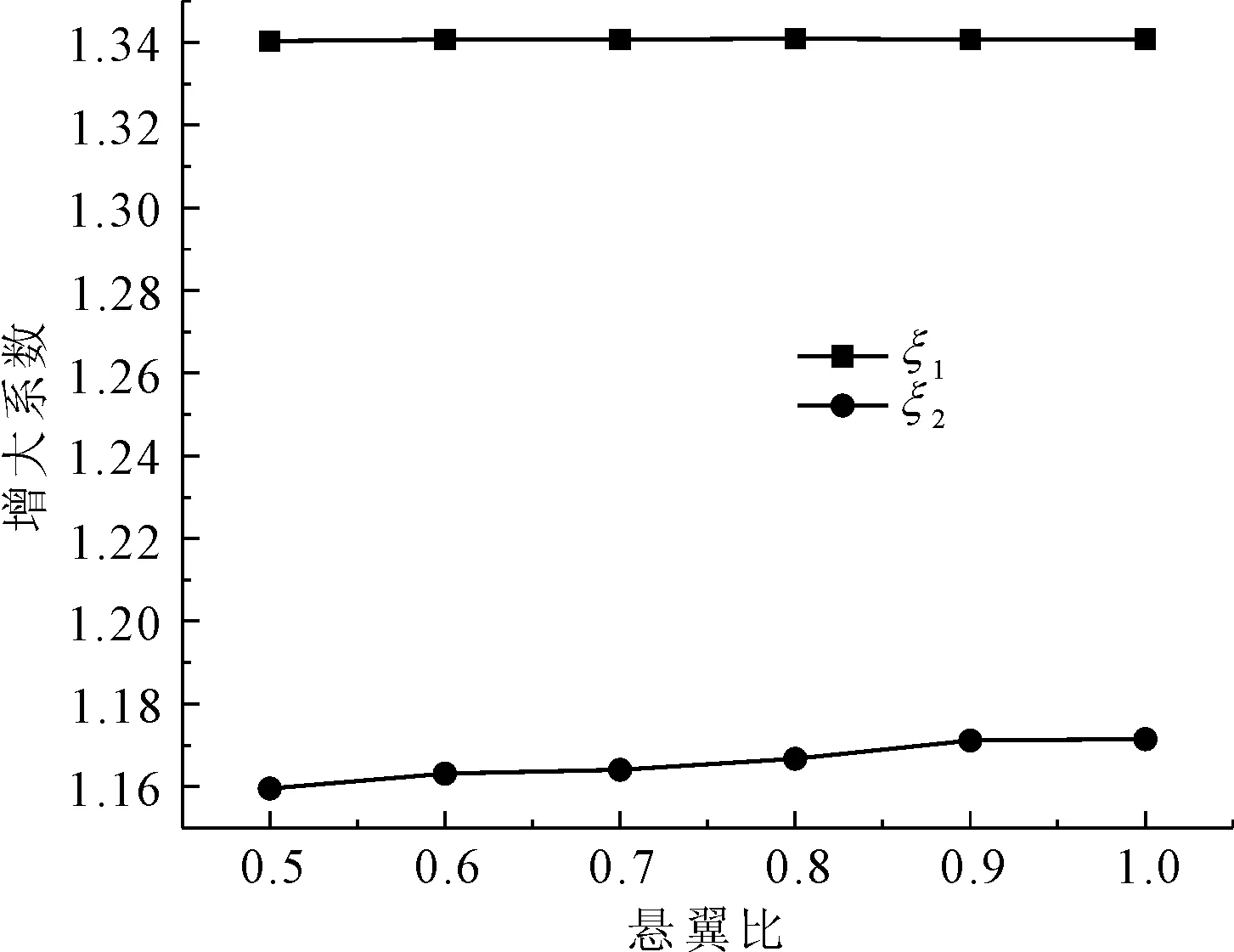
图9 悬翼比对ξ1和ξ2的影响

2.3 高跨比

H/L定义为梁高与计算跨度的比值，跨度为35 m,将H/L从0.05开始，增量为0.01,最终至0.1，则H=1.75 m、2.10 m、2.45 m、2.80 m、3.15 m、3.50 m，其余尺寸不变，建立6个有限元模型。绘制变化曲线见图10.

图10 高跨比变化时的增大系数

由图10可知，ξ1和ξ2随高跨比的增大单调递增，而且增大幅度均较大，ξ2的增幅明显大于ξ1，ξ1增幅逐渐变缓，而ξ2随高跨比增加近乎成一条斜直线，且斜率较大。变化曲线说明高跨比对偏载系数的影响敏感度较高，经验系数法相对于ξ1和ξ2仍偏于不安全。

2.4 宽跨比

将2b/L定义为宽跨比。跨度为35 m,将2b/L从0.08开始以0.02为增量，增至0.18,则2b=2.8 m、3.5 m、4.2 m、4.9 m、5.6 m、6.3 m,从悬翼比的影响分析来看，悬臂板长度影响很小，取1.5 m，其余尺寸均不变，建立6个有限元模型，绘制结果见图11。

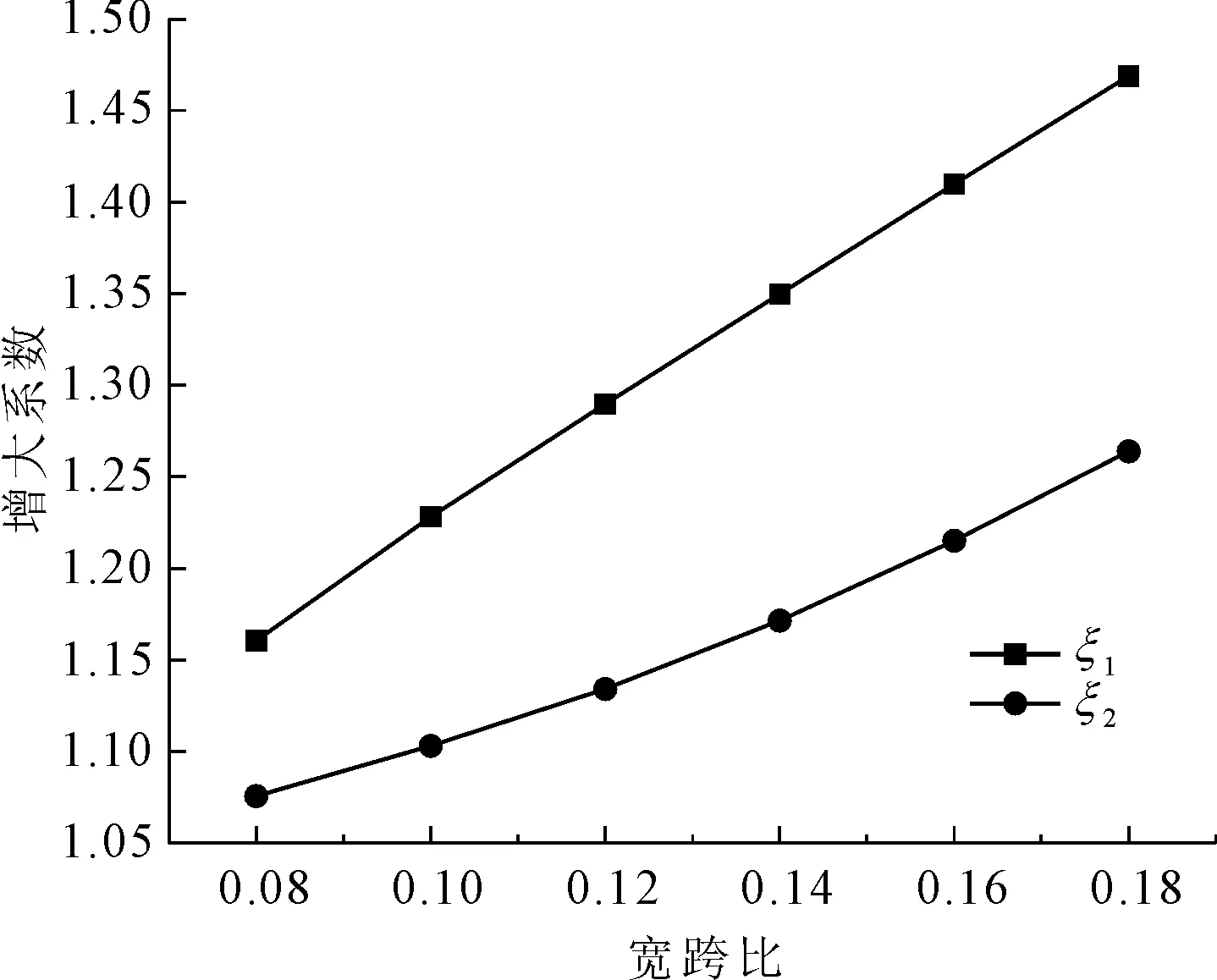
图11 宽跨比变化时的增大系数

由图11可知，ξ1与ξ2随宽跨比的增大单调递增，且增幅均较大，ξ1增幅大于ξ2，ξ2增幅由小变大，而ξ1随宽跨比的增加几乎呈斜直线状态，且斜率较大，最大值与最小值相差0.3之多，敏感度较高。

2.5 参数相关性比较

从图12和图13可看出，对偏载系数影响最大的是宽跨比，其次依次是高跨比和腹杆壁厚，悬翼比变化对钢桁腹-混凝土组合箱梁的偏载系数影响最小，在分析该结构偏载系数时可以忽略其影响。

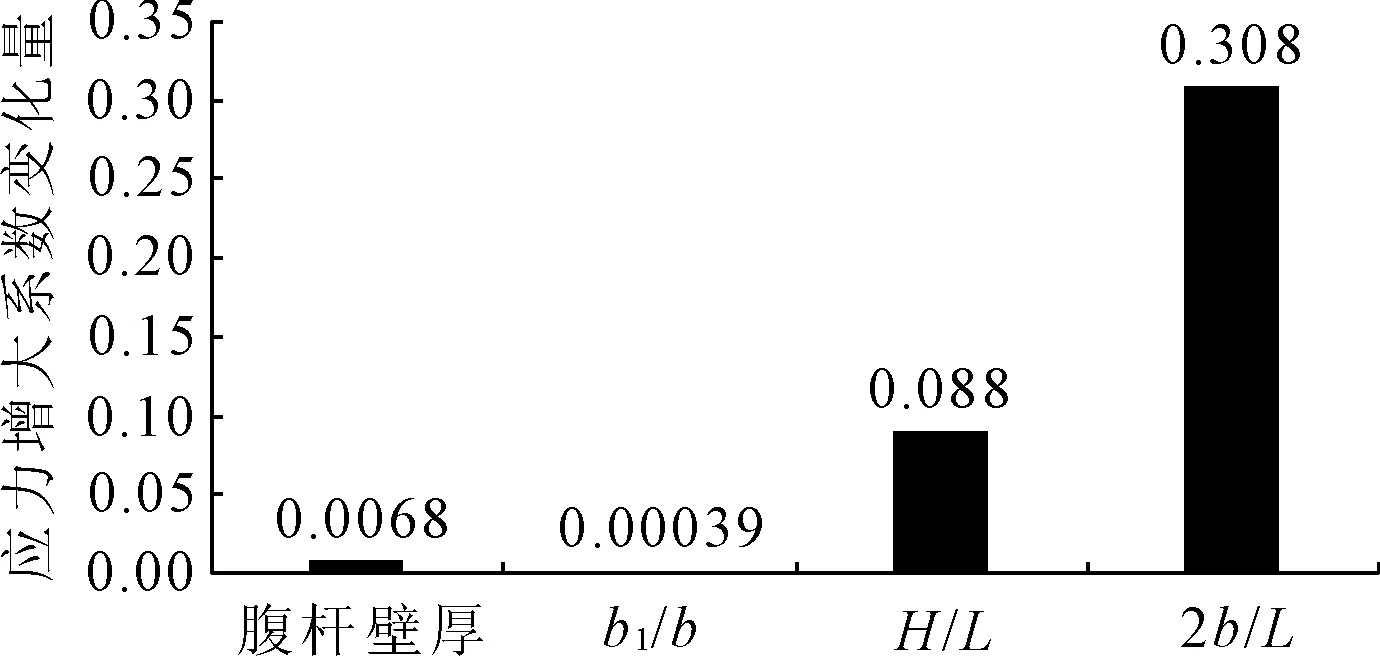
图12 应力增大系数变化量

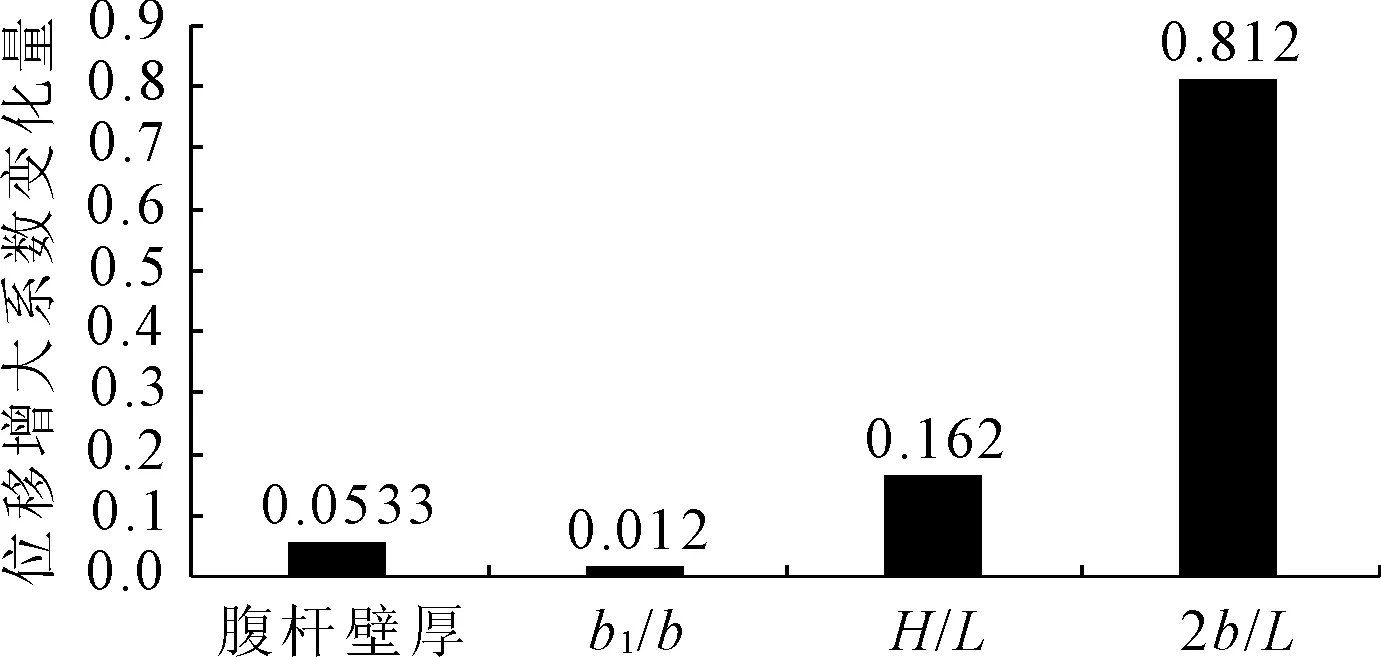
图13 位移增大系数变化量

3 理论计算

文献[14]已验证修正的偏心压力法比偏心压力法和经验系数法更能较为准确地计算桥梁的偏载系数。为验证应力和位移增大系数方法是否能较为准确的计算出偏载系数，现采用修正的偏心压力法公式计算出数值与之作比较。由于宽箱梁宽跨比比较大，偏载系数计算有其独特的计算方法，传统的计算方法不适用于宽箱梁[11]，所以就选取腹杆壁厚的变化这组模型来进行验证。

计算组合结构的偏载系数，首先要采用腹板换算法将钢桁腹杆换算成混凝土腹板。采用文献[8]按剪切变形相等的原理进行了钢桁腹杆与混凝土板的换算，换算混凝土板厚公式如下：

(3)

式(3)中Tc为换算后的连续混凝土腹板厚度，Ef为钢桁腹杆的弹性模量，A为钢管的截面面积，Gc为混凝土剪切模量，Gc=0.4Ec，Hc为换算后的混凝土腹板高度，即钢桁腹杆的垂直高度。

修正的偏心压力法计算公式如下：

ξ=nK

(4)

(5)

式(4)中ξ为偏载系数，n为箱梁截面的腹板总数，式(5)中K为荷载横向分布系数，e为偏心距即作用点到截面中心的距离，ai为第i腹板到截面中心的距离，aw为外侧腹板到截面中线的距离，而β为修正系数，表达式为:

(6)

式(6)中 ，L为桥梁计算跨度，G、E分别为抗剪抗弯弹性模量，Ix、It分别为抗弯抗扭惯性矩[15]。

计算方法如下[16]：

(7)

式(7)中的w、t1、t2、t3、t4、a、h如图14所示。

根据式(3)—式(7)计算出的各数据如表3所示,应力、位移增大系数分别用ξ1和ξ2表示。

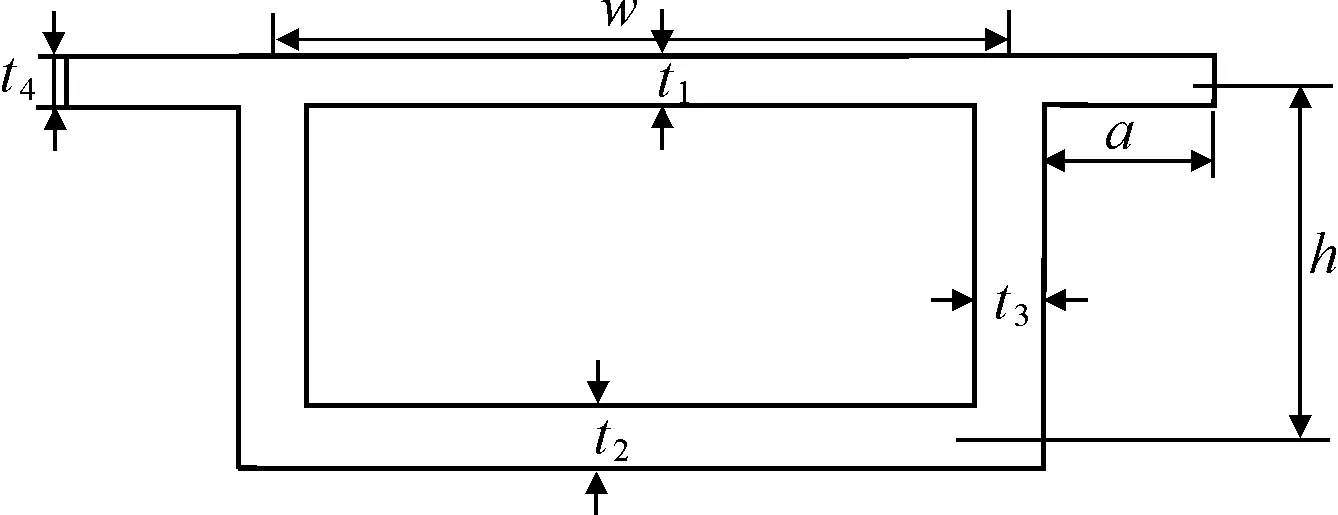
图14 各参数表示图示

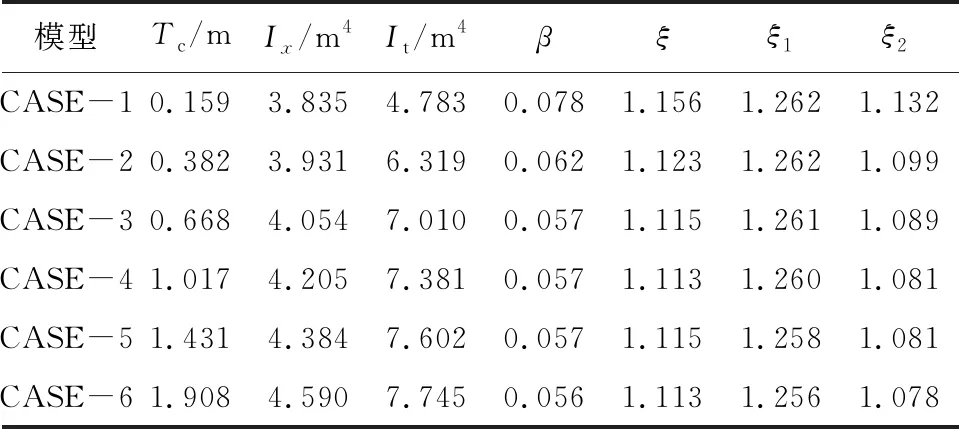
模型Tc/mIx/m4It/m4βξξ1ξ2CASE-10.1593.8354.7830.0781.1561.2621.132CASE-20.3823.9316.3190.0621.1231.2621.099CASE-30.6684.0547.0100.0571.1151.2611.089CASE-41.0174.2057.3810.0571.1131.2601.081CASE-51.4314.3847.6020.0571.1151.2581.081CASE-61.9084.5907.7450.0561.1131.2561.078

从表3和图15来看，用修正偏压法计算出的偏载系数大小介于应力增大系数和位移增大系数之间，而且更加接近于位移增大系数。走向趋势也与位移增大系数相近，说明位移增大系数更接近实际的偏载系数，而应力增大系数更加偏于安全。

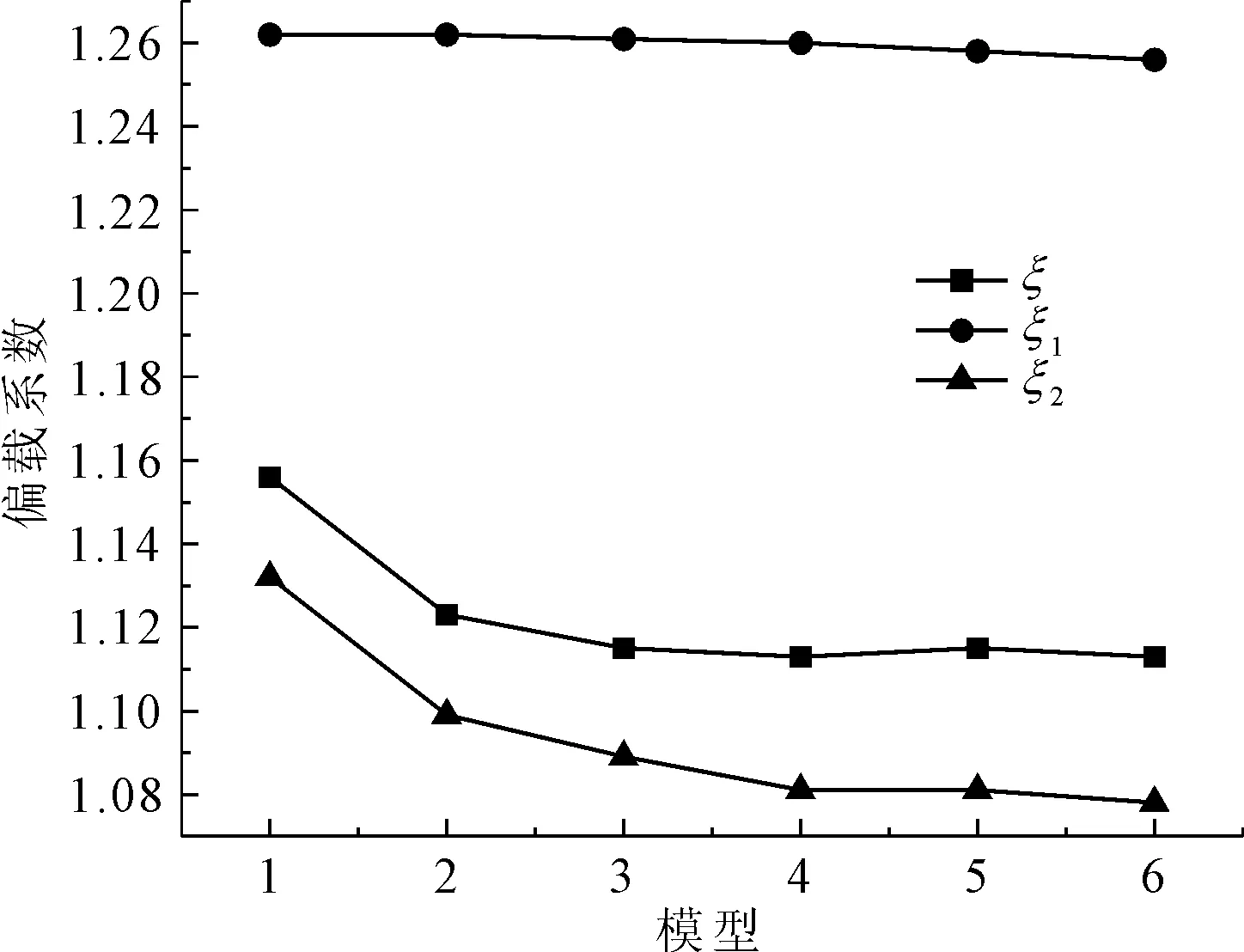
图15 偏载系数比较

4 结 论

(1) 实际工程中，偏载系数计算方法的不同能够造成很大的误差，本文得出应力大多数情况下都大于位移偏载系数。将偏载系数计算方法详细地分为应力和位移两种不同的计算方法，遇到实际问题再做具体分析。

(2) 偏载系数随高跨比和宽跨比的增加单调递增，随壁厚增加而单调递减。宽跨比对钢桁腹-混凝土组合结构偏载系数影响最大，其次是高跨比和腹杆壁厚，悬翼比的影响最小，可以忽略不计。

(3) 由经验系数法取值得出的1.15对钢桁腹-混凝土组合箱梁并不完全适用，只是在位移增大系数中较为适用，将该结构箱梁的经验系数值提高为1.2更为安全，但在实际应用中还需通过计算分析确定其偏载系数。

(4) 在箱梁宽度不是太大的前提下，位移增大系数更加接近于修正偏心压力法计算出的偏载系数，而应力增大系数更为安全。