农业植保无人机变结构线性滚动时域估计器研究

楚红雨 倪俊超 常志远 邵延华 张晓强

(西南科技大学信息工程学院， 绵阳 621010)

0 引言

植保无人机的航迹规划是保证其完成植保作业任务的关键技术，高精度、低延时的位置估计算法一直是该领域的研究重点[1-2]。位置估计器需要融合多传感器的异构数据，例如，植保无人机的定位可以通过融合嵌入式传感器提供的测量数据，然后估计出植保无人机实时的位置信息。当位置估计器融合惯导数据和GPS导航数据时，数据采样过程中存在多传感器采样频率不同而造成的延时，从而影响位置信息估计的准确性[3-4]。

目前，国内外学者对多传感器采样频率不同造成的延时问题展开了研究。文献[5]提出使用预测器来补偿延时的方法，但是将预测器应用到系统中会增加计算时间和内存使用率，不适用于计算资源有限、实时性较高的飞控系统。文献[6]提出了3种不同的优化方法处理多目标无序测量造成的延时问题，其中CISI (Complete in-sequence information)方法效果最好，但是该方法结构比较复杂。文献[7]根据历史测量值，利用其中的延时测量值重新估计整个后验状态序列，通过数值模拟的方法进行验证。文献[8]设计了一个正则化方法，并在滚动时域估计器(MHE)中给出一个具体的代价函数，根据丢失的数据自适应调整权重来处理延时问题，但该方法只针对单采样频率的延时，对于多采样频率的延时尚有待验证。文献[9]提出了一种用于处理时滞测量的MHE，但是在快速实时在线处理和传感器多采样频率方面需要进一步研究。

针对以上问题，本文利用变结构线性滚动时域估计器(VSL-MHE)来解决因多传感器采样频率不同而造成的延时问题，以提高植保无人机位置估计器的准确性和鲁棒性。

1 植保无人机动力学模型

1.1 坐标系定义

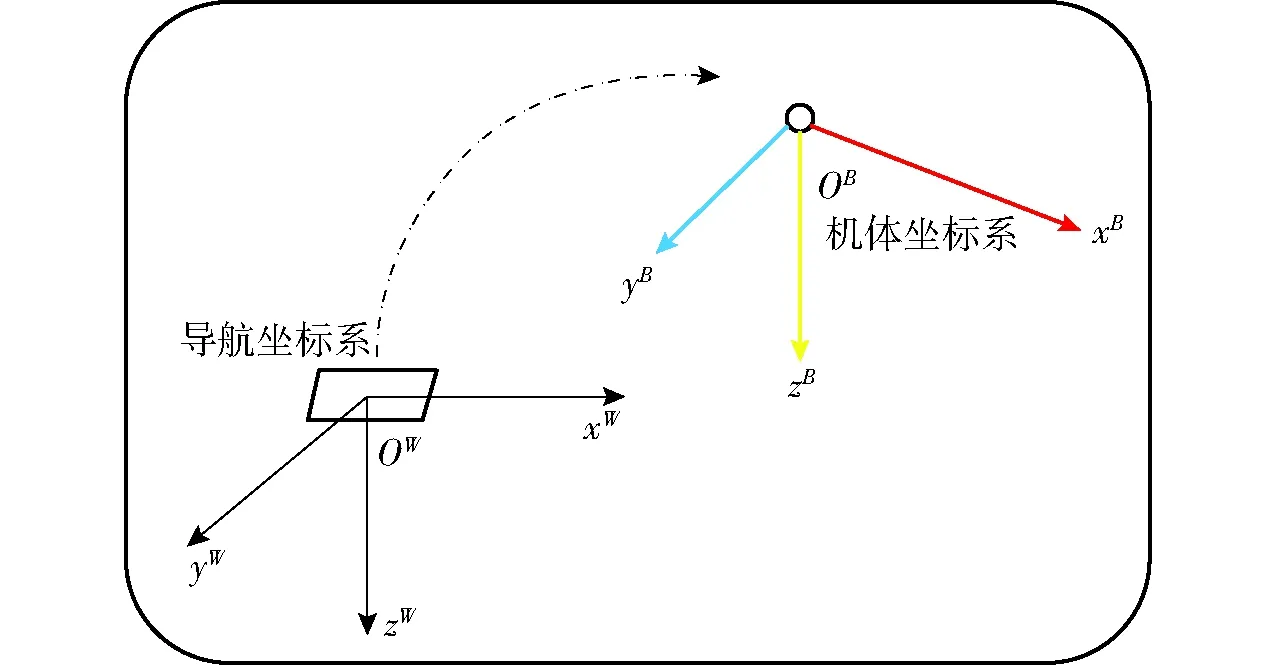
图1 植保无人机坐标系系统Fig.1 Coordinate system of plant protection UAV

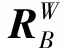
1.2 动力学模型

使用牛顿-欧拉法对植保无人机进行动力学建模，动力学模型表征了飞行器受力和运动之间的关系。完整的动力学模型形式过于复杂，文献[10]中对四旋翼无人机动力学模型进行了简化，具体形式为

(1)

式中sW——植保无人机的位置

vW——植保无人机的速度

aW——导航坐标系下的实际加速度

式(1)中，加速度和位置的测量模型为

(2)

式中aB——机体坐标系下的加速度测量值

abias——加速度偏移值

aτ——加速度计测量值中的高斯白噪声

sτ——GPS和气压计测量值中包含的高斯白噪声

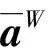
(3)

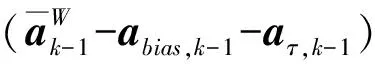
xk=Axk-1+Buk-1+Nwk-1

(4)

式中A——状态转移矩阵

B——输入矩阵

N——过程噪声矩阵

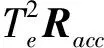
(5)

测量方程可表示为

zk=Cxk+νk

(6)

式中νk——测量噪声，νk∈R3×1

2 位置估计器设计

2.1 滚动时域估计器

滚动时域估计器(MHE)是一种基于时域的优化方法，利用过去有限的测量值进行估计，其窗口的最后一个输出作为当前状态估计[11]。通过将估计问题转化成优化问题进行求解，可以显式地表示约束，并求解状态估计量。通常这些约束也更能反映实际情况，因此可以提供更多信息，缩小估计器的搜索空间，提高搜索效率，使其能够在嵌入式处理器上高效可靠地运行，估计植保无人机的实时位置。

将式(4)、(6)离散化，可表示为

(7)

式中uk——k时刻的输入矢量，uk∈R3×1

zk——k时刻的测量矢量，zk∈R3×1

对状态估计量施加约束

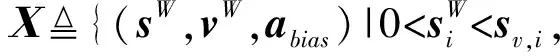
(8)

式中X——状态可行集

sv,i——植保无人机的位置约束值

vw,i——植保无人机的速度约束值

at,i——加速度偏移的约束值

式(7)中的xk为9维状态，包含3维位置、3维速度和3维加速度偏移。假设过程噪声wk和测量噪声νk为零均值高斯白噪声，其协方差矩阵分别为Qk和Rk。

对式(7)中的每个工作点线性化，可导出测量序列{zk}的线性描述为

(9)

式(9)中状态估计可以表述为MHE问题，即

(10)

式中，x0是初始状态，该问题将受到约束限制，其状态变量xj在状态可行集X中的取值为xj∈X(j=0,1,…,k-1)。

式(10)中的代价函数表示为

Γk(x0,{wj}(j=0,1,…,k-1))

(11)

式中S——测量部分范数权重矩阵

L——噪声部分范数权重矩阵

随着时间的推移，式(10)中将获得传感器更多的信息，计算的复杂度随着时间的增加而增加，这将使得有限资源下在线计算的实时性无法保证。为了避免这一问题，文献[12]提出了一种固定维数的滚动时域估计方法。通过该方法，代价函数(11)可以改写为

(12)

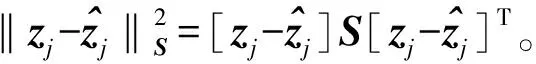
将式(12)作为MHE中的代价函数，MHE的计算量随着采样次数线性增加，当到达窗口NP的边界时，MHE的计算量基本保持不变。

上述算法在实际应用过程中，由于多传感器数据的采样之间存在延时，会造成位置估计信息不准确，使得植保无人机定位精度变差，导致作业过程中出现喷洒面不均匀的情况。

2.2 变结构滚动时域估计器

测量数据存在延时，会影响到控制器的性能。如果MHE具有可变结构，便可以处理由于多传感器采样频率不同而造成的数据之间延时问题。如图2所示，通过零阶保持块(ZOH)对IMU、气压计和GPS进行采样，在位置融合周期内，IMU采样频率大于气压计和GPS的采样频率。位置融合更新的时间点上GPS相对于IMU的延迟为d1,d2，…,dk。

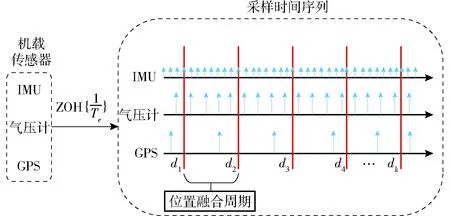
图2 传感器数据采样延迟示意图Fig.2 Delay of sensors data acquisition

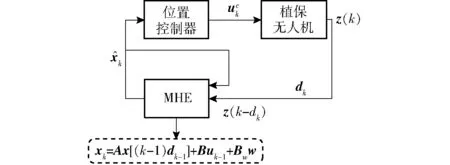
图3 考虑数据延时的系统结构示意图Fig.3 System block diagram with data delay

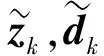
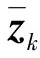
(13)

式中H——状态转移矩阵，NP-dn为与GPS输出之后最接近的惯导输出时刻

Θ——与H相对应的控制矩阵

按序展开后的H与Θ矩阵序列分别为

(14)

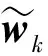
(15)

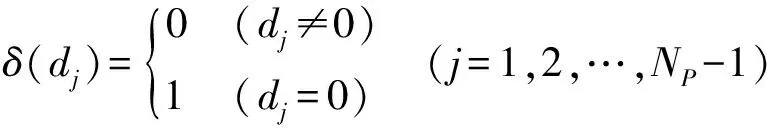
dj为k时刻窗口NP内的延迟位置，当在j序列上dj为0时，则表示需要将对应的Sk进行更新。

综上所述，实际应用中，VSL-MHE的运行过程如图4所示。

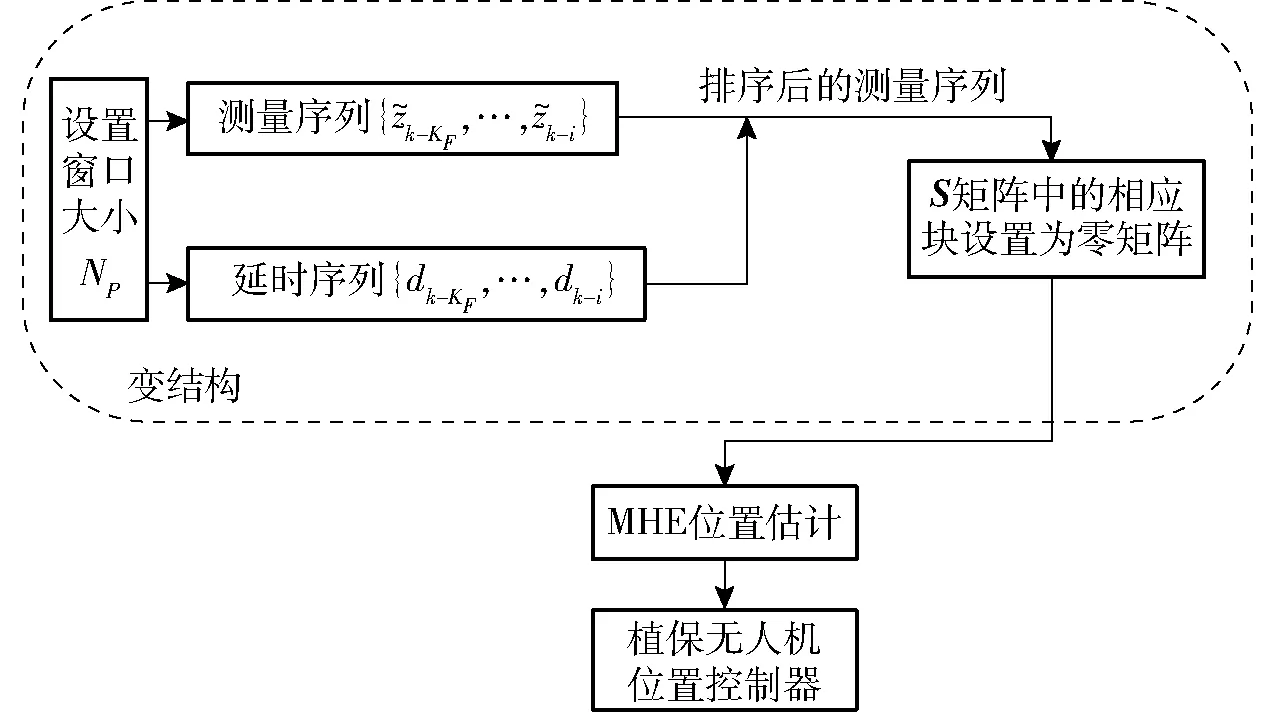
图4 VSL-MHE算法运行过程Fig.4 Iterative process of VSL-MHE algorithm

值得注意的是，矩阵S接收到的新测量矢量值是变化的，但其维数保持不变。如果一个测量值在k时刻到达，并且该值在窗口NP内，则通过将矩阵S的块移动到窗口NP中相应的位置，完成矩阵S的更新。

3 算法验证与飞行实验

当前循环迭代卡尔曼滤波器(CIEKF)是多旋翼无人机常用的位置估计方法[13]，为了评估位置估计器的性能，将CIEKF、MHE与VSL-MHE进行比较，使用均方根误差(RMSE)来度量估计器的精度，定义为

(16)

式中δ∈{CIEKF,MHE,VSL-MHE}，NR为采样次数，在采样范围[0,NR-1]内的实际值和估计值分别表示为xi和i(i=0,1,…,NR-1)，为了比较上述两种位置估计器在相同传感器延时条件下的性能，定义ηδ为

(17)

如果ηδ为负数，则表示VSL-MHE估计的位置精度高于MHE和CIEKF，值越小表征位置估计器的性能越好。

3.1 实验平台

为了验证VSL-MHE的精度，在室内使用OptiTrack运动捕捉系统，为植保无人机提供可调输出频率的模拟GPS信息，同时也可获得植保无人机的精确位置。在该系统下对基于VSL-MHE、MHE和CIEKF的位置估计算法进行定量评估。运动捕捉系统的主要组成部分包括：12个Flex3红外摄像头、无线路由器、标记点、工作站和光学运动捕捉软件[14]。通过OptiTrack可实时获取植保无人机的位置信息，精度可达0.1 mm。利用无线路由器将位置数据传输到树莓派3B+，进行坐标转换后发送到飞控系统。图5为室内模拟系统结构图。实验场地长8 m、宽8 m、高3 m，为了模拟GPS的发送频率，设置运动捕捉系统的位置发送频率为2～20 Hz。

植保无人机实验平台如图6所示，采用四旋翼结构，每个旋翼可提供9.8 N的升力，总共可以提供最大39.2 N升力，能持续飞行15 min。植保无人机的结构参数如表1所示，位置输入单元使用Neo-

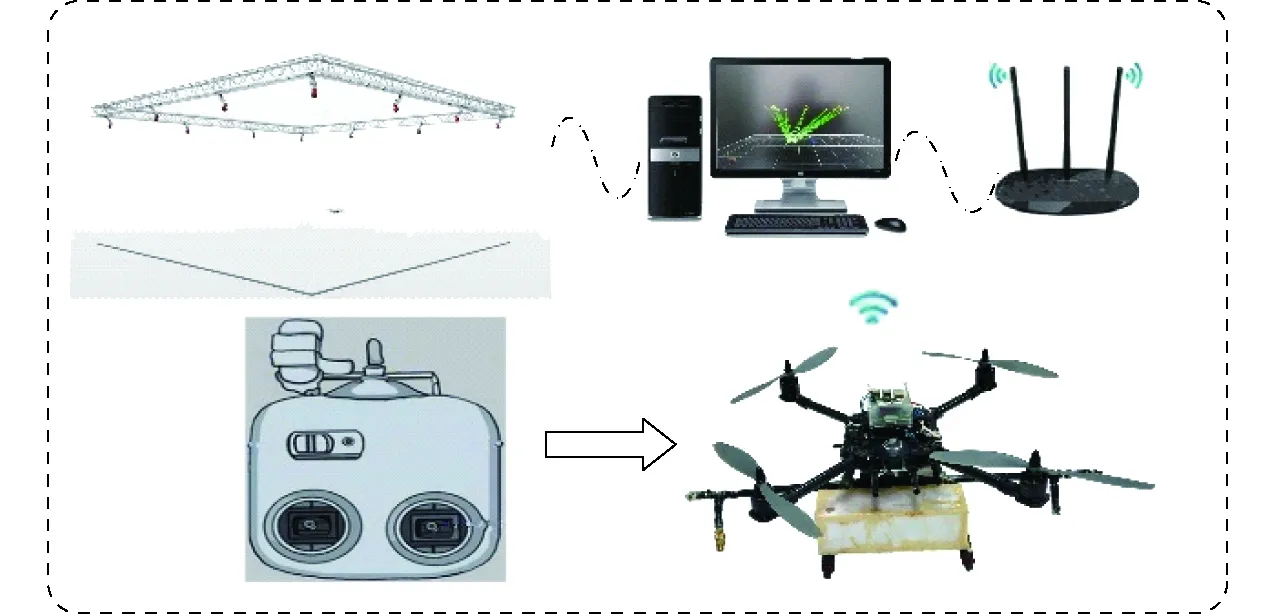
图5 室内模拟系统结构Fig.5 Structural diagram of indoor simulation system

图6 植保无人机实验平台Fig.6 Experiment platform of plant protection UAV1.喷头1 2.水泵 3.飞控系统 4.树莓派3B+ 5.GPS模块 6.喷头2 7.水箱

参数数值空载质量/kg2.0满载质量/kg3.5飞行器轴距/cm50螺旋桨桨径/cm11电池容量/(A·h)6飞行速度(室内/室外)/(m·s-1)0.2/2.0

M8N GPS模块，机载惯导单元为MTI-2模块，该模块集成了三轴加速度计、三轴陀螺仪和三轴磁力计[15]。高度测量模块为MS5611，垂直精度可达10 cm。

利用GPS和惯导数据，在飞控系统上运行VSL-MHE、MHE和CIEKF算法实现位置估计解算，引导植保无人机完成作业任务，分别在室内和室外两种环境下进行验证。

3.2 室内仿真飞行测试

植保无人机在OptiTrack运动捕捉系统下测试位置估计算法，图7为植保无人机室内飞行测试场景。

图7 运动捕捉系统辅助下的室内飞行测试场景Fig.7 Indoor flight under motion capture system

为了模拟GPS数据的延时，OptiTrack运动捕捉系统的位置输出频率分别为2、5、10、20 Hz，并加入零均值高斯白噪声干扰。其中2 Hz的模拟GPS输出频率相对于机载惯导的延时时间差最高约为500 ms。

植保无人机分别在VSL-MHE、MHE和CIEKF位置估计器的辅助下完成定点悬停[16]，每次悬停时间5 min，悬停高度为1.5 m，分别在发送频率为2、5、10、20 Hz下测试悬停精度。

(18)

评估两组位置估计器的性能，图8展示了植保无人机悬停于设定位置时GPS不同发送频率导致的最大位置偏差。

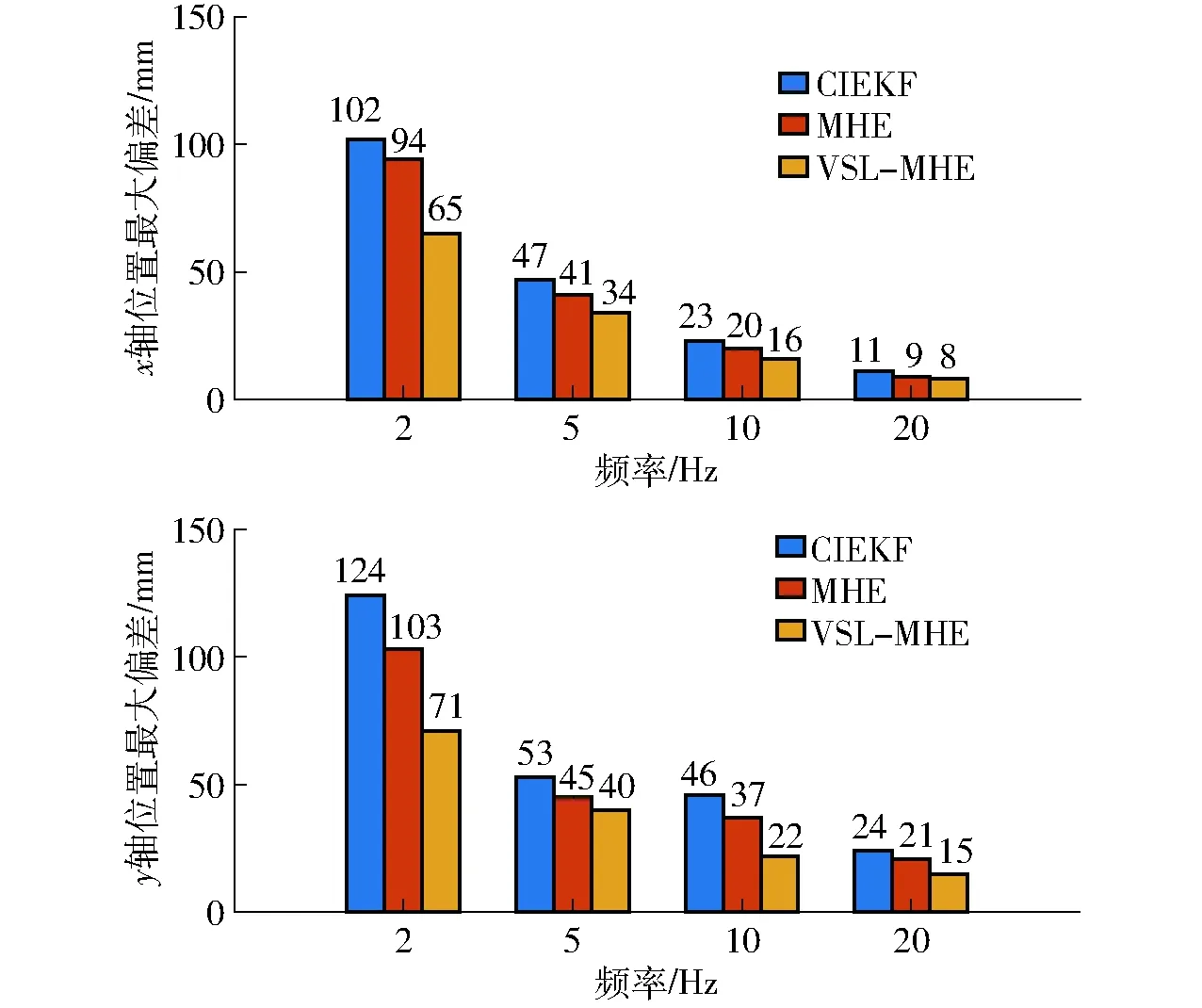
图8 不同位置发送频率下的最大偏差Fig.8 Maximum deviation under different frequencies

从图8分析可知，位置发送频率从20 Hz到2 Hz逐渐降低时，3种位置估计器估计的位置最大偏差也同时增加，当频率为2 Hz时，CIEKF、MHE和VSL-MHE位置估计器在x轴和y轴方向估计的位置最大偏差都达到最大值，分别为102、124 mm，94、103 mm，65、71 mm，VSL-MHE位置估计值相比于MHE和CIEKF的位置估计值，在x轴方向和y轴方向的偏差分别降低29、32 mm和37、53 mm。在图8中x和y轴的位置最大偏差中，2 Hz的模拟GPS输出频率造成的位置偏差明显大于其他频率，说明位置估计中惯导测量值的融合计算需要使用GPS信息进行修正，且在一定范围内GPS的输出频率越高修正速度越快，引起的位置偏差也越小。20 Hz频率下，CIEKF、MHE和VSL-MHE估计的位置最大偏差在x轴方向和y轴方向分别为11、24 mm，9、21 mm，8、15 mm，远小于2 Hz频率下的位置最大偏差。上述分析表明，当GPS的信息输出频率因受到干扰而降低时，相对于CIEKF和MHE，使用本文中设计的VSL-MHE位置估计算法能够减小位置偏差，提高定位精度。

3.3 室外飞行测试

上述通过位置最大偏差实验证明了VSL-MHE算法的有效性，为了进一步在真实环境下验证算法的鲁棒性，在室外进行了MHE、VSL-MHE和CIEKF位置估计算法的对比测试。图9为植保无人机室外飞行实验环境。

图9 室外飞行实验环境Fig.9 Environment of outdoor flight test

在室外已知环境下进行植保无人机的位置估计器性能测试，确定衡量飞行方式优劣的标准有时间、能耗和路程[17]。考虑本实验中植保无人机的系统参数和测试对比实验的一致性，采用图10所示的40 m×30 m范围的往复式航线[18-19]。在地面站中设置往复式航线，将其同步到飞行控制系统。该航线单节长30 m，相邻航线间距8 m，飞行高度为3 m。在相同的条件下对MHE、VSL-MHE和CIEKF位置估计算法分别进行8次实验，实验数据以50 Hz的频率存储在机载SD卡用于后续的数据分析。

图10 室外飞行轨迹示意图Fig.10 Outdoor flight path diagram

实验中以时间间隔tf位置估计器的输出值与位置设定值的均方根误差RMSE来定量衡量位置偏离程度，RMSE值越大代表位置估计器性能越差[20]。

图11中展示了8次实验数据的误差比较。从图11中分析可知，植保无人机x、y轴方向位置RMSE由大到小为：CIEKF、MHE、VSL-MHE，表明VSL-MHE位置估计算法相对于CIEKF能够提高位置估计精度，并且对比MHE，由于使用了变结构的方法，VSL-MHE的位置估计精度比MHE有所提高。x轴方向位置RMSE值小于y轴方向位置RMSE值，是由于x轴方向的航线远小于y轴方向的航线。图12为两组对比实验，分别为VSL-MHE与MHE之间x轴方向与y轴方向的ηδ值，VSL-MHE与CIEKF之间x轴方向与y轴方向的ηδ值。图12的实验结果同样表明了VSL-MHE的位置估计精度要高于MHE和CIEKF的位置估计精度。

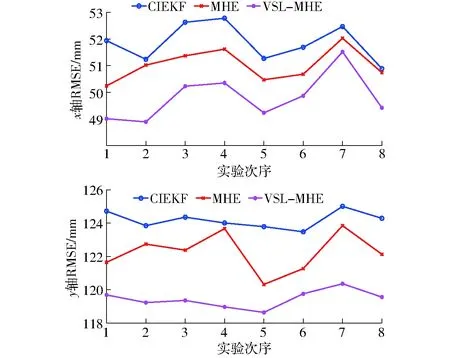
图11 植保无人机位置的RMSEFig.11 RMSE of UAV position

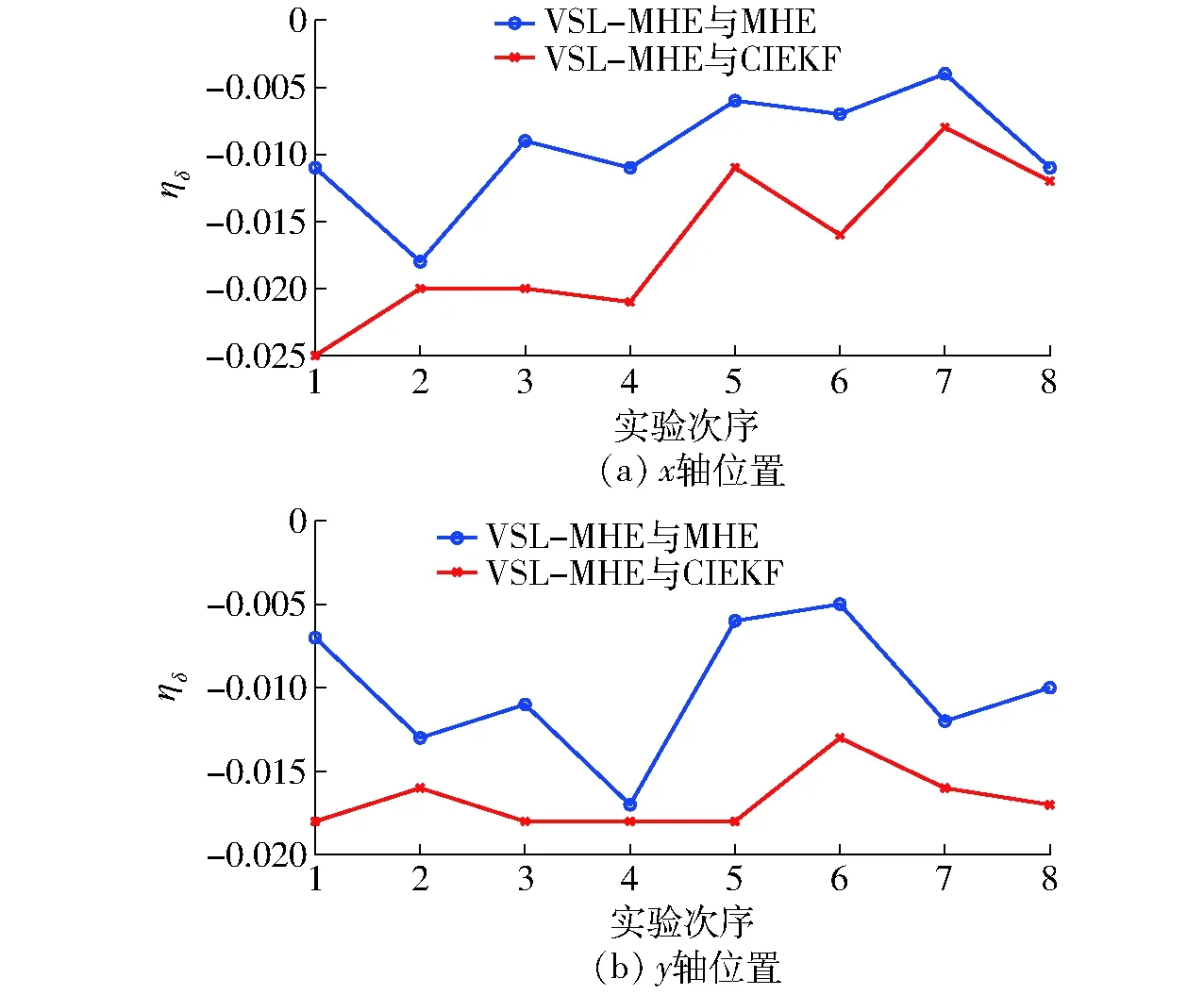
图12 3种位置估计器之间的ηδFig.12 ηδ between three position estimators

分别将8次VSL-MHE、MHE和CIEKF位置估计数据经过均值处理，处理过程定义为

(19)

式中，P∈{CIEKF,VSL-MHE,MHE}，在T次实验内，x轴和y轴方向的位置均值表示为(Px,Py)。图13为3组实验的位置估计精度对比图。

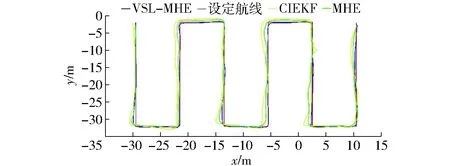
图13 位置估计器精度对比Fig.13 Accuracy comparison of position estimator

从图13中可知，植保无人机在拐点处，偏航需要旋转90°，此时造成的位置偏差最大。因为在植保无人机的姿态控制中，偏航角响应时间大于横滚角和俯仰角的响应时间，一般情况下控制植保无人机偏航旋转10°需要的时间是控制横滚角和俯仰角的2倍[21]。CIEKF估计出来的位置信息，在实际飞行中与实际位置在x轴方向和y轴方向的最大偏差分别为1.1 m和0.95 m，而MHE和VSL-MHE估计的位置信息与实际位置在x轴方向和y轴方向的最大偏差分别为0.87、0.62 m和0.48、0.59 m。所以在整个室外飞行过程中，VSL-MHE为植保无人机提供的位置精度高于CIEKF和MHE。即使GPS模块的数据输出频率只有10 Hz，通过VSL-MHE仍能进行较为准确的状态估计，体现了室外真实作业环境中该算法的有效性。

4 结束语

为了解决多传感器采样频率不同造成的延时影响，设计了一种变结构线性滚动时域估计器，用于提高植保无人机位置估计的准确性。通过将VSL-MHE位置估计器与CIEKF和MHE位置估计器进行比较，对估计精度进行分析。室内场景下飞行测试表明，随着位置输出频率由20 Hz降低到2 Hz，位置估计器的精度也随之下降，与CIEKF、MHE位置估计器对比，VSL-MHE能很好地抑制延时的影响，验证了VSL-MHE位置估计器的位置估计精度。在室外真实作业场景下，将3组位置估计器用于植保无人机定位，分别进行了8次实验，并计算ηδ值，结果表明ηδ均为负值，表明VSL-MHE位置估计器的精度优于CIEKF和MHE。利用VSL-MHE设计的位置估计器具有精度高、鲁棒性强的特点，适用于植保无人机对室外动态性能要求较高的位置信息的解算。