基于单幅老照片的历史建筑三维重建

2019-11-04石若明

北京建筑大学学报 2019年3期

丁波，石若明

(北京建筑大学测绘与城市空间信息学院，北京 100044)

历史建筑是国家的年轮和记忆，历史上许多令人惊叹的伟大建筑物，由于战乱、自然环境变化及城市发展，一些古老建筑现已消失，仅存于文字记载. 近代随着照相技术的出现及发展，一些古建筑被实体照片所记录，利用老照片对其进行复原研究，对文化和建筑研究具有重要意义，也是对中国古文化的发扬光大. 虚拟现实利用计算机技术对已消失建筑和文物进行原貌恢复和展示，因此具有广泛的应用前景[1].

计算机构建物体三维模型的方法主要有基于几何造型的方法、基于建筑及地形图纸的半自动化建模方法、用三维激光扫描仪等获取三维模型的方法和基于影像的自动化建模方法[2]. 利用现有的建筑地形图纸生成三维模型，如Maya、3dmax、Sketchup等，通过点、线、面、体等几何元素的平移、转换等几何变换产生实际物体的数字模型. 此方法具有良好的交互性，但真实感差，需要操作人员具有丰富的专业知识，且工作量大[3]. 三维激光扫描在构建模型所需时间相对较少，广泛应用于逆向工程、虚拟现实等，可获取精确的三维模型，但成本高，且只能扫描现存建筑，故不在本文讨论范围. 传统的摄影测量一般需要从两个或两个以上角度对同一目标摄影获取的立体像对，利用摄影测量或计算机视觉技术的原理，解算关键点的三维坐标；消失建筑或残存建筑无像对，只有单张相片，因此使用基于射影几何的方法进行单片建筑物重建，利用影像的透视变形等信息，从存在这种变形的成像中得到建筑物的三维数据[4]. 本文主要针对单张相片建模工作进行相应研究.

利用单张相片进行建模工作，蒙印[5]研究了透视图中人工构筑物具有大量的平行线，在理想情况下，与影像平面相交的空间平行直线束在影像上的投影将汇聚于同一点，利用这个几何特性，可以解求影像的内、外方位元素，恢复数码相机的空间姿态，并结合相应地形图数据，获取建筑物的高程数据. 何桂珍等[6]研究了基于单幅影像的快速三维重建，以某一小型建筑三维重建为例，分析了以体为基本单元和以平面为基本单元的两种影像建模方法. 韩艳丽等[7]研究了单幅影像中将平行线分成分别平行于X、Y、Z坐标轴线的三组平行线，然后利用间接平差，求得它们的灭点X∞、Y∞、Z∞，进而求取影像的内方位元素x0、y0、f与三个角元素φ、ω、κ，并在假定房屋长度为L基础上，同时解求影像的摄站坐标XS、YS、ZS与房屋的宽度w、高度h，构建建筑物几何模型，进行纹理贴图，从而实现房屋的三维重建. 闫霖[8]提出在透视影像中进行长度量测和坐标量测的方法，可以作为在透视影像中获取信息的有效手段，利用灭点进行相机检校和计算影像的外方位角元素，并以影像中的某个平面作为基准面的前提下，利用射影几何中的交比等方法，量测与基准面垂直和平行的线条长度，在透视影像中建立三维坐标系，并在影像中的坐标轴平面上进行三维坐标量测的方法，实现单幅影像进行三维重建. 王思洁等[9]提出了一种基于结构化场景的单张图像建筑物三维重建方法，先基于RANSAC算法及最小距离法分别解算灭点直线和灭点，然后基于平行平面、包含平行信息的任意平面和包含垂直信息的任意平面的平面模型解算三维坐标，实现三维建模. 刘春燕等[10]等利用单张影像规则建筑物在影像中的灭点信息，在已知内方位元素的情况下，推导出现有二维GIS数据的辅助下解求影像外方位元素公式，从单张影像上量测建筑物高程的数据方法.

1 单张相片建模原理

首先收集对老旧建筑或消失建筑所记录的照片数据，利用求出的三个正交方向的灭点数据，根据灭点与像片内、外方位元素之间的几何关系，进行单张建筑物照片的标定，得出内方位元素，并结合相应的地形图及其比例尺关系，获取建筑物高程数据信息[11]. 依照建筑物侧面纹理信息，及传统建筑物的屋顶、门窗、台阶等造型尺寸的先验知识，使用建模软件对建筑物进行三维建模，在此基础上结合3D打印技术，实现数字模型到实体模型的转化(图1).

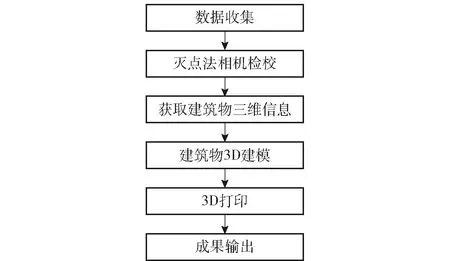
图1 总体流程图Fig.1 Overall flow chart

1.1 灭点法相机标定原理

在透视投影下，空间平行的直线在像平面上汇聚到一点，该点称为灭点. 当被摄物体表面存在丰富的有规律性的直线信息时，可以用灭点法进行相机标定[12]. 对于规则的立方体建筑物进行单张摄影时，根据建筑物本身的几何条件约束，构造三个正交方向的灭点X∞、Y∞、Z∞如图2所示，相应三个灭点在空间坐标系下与影像内、外方位元素的Z∞几何关系如图3所示.

图2 灭点示意图Fig.2 Vanishing Point Diagram

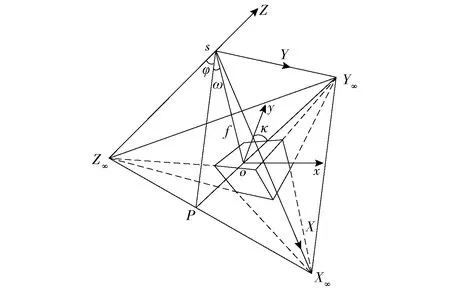
图3 灭点与外方位元素之间关系Fig.3 The relationship between vanishing points and exterior elements

如图3所示图像中三个正交方向的灭点为X∞、Y∞、Z∞,即为三点透视，摄影中心为s，o为相机主点(x0，y0)，f为相机的焦距，P为o与Y∞的延长线与线段X∞Z∞的交点，三个外方位角元素分别为φ=∠PsZ∞,ω=∠Pso，κ=∠yoY∞. 灭点和摄影中心的连线与形成该灭点的空间平行线平行，三个正交方向X、Y、Z的直线所形成的灭点必落在相应的坐标轴上. 因此s-X∞Y∞Z∞是直角三角锥，s垂直于三角形X∞Y∞Z∞，则相机主点o为三角形X∞Y∞Z∞的重心[13].

影像主点：是由三个灭点构成的三角形的重心o：

(x0,y0)

(1)

焦距：

f2=-(xX∞-x0)(xY∞-x0)+
(yX∞-y0)(yY∞-y0)

(2)

在直角△osY∞,△osX∞,△sX∞Y∞中，

几何关系：

(3)

(4)

转换为坐标关系：

(5)

(6)

即可得出焦距公式.

1.2 获取建筑物三维信息

由相机拍摄得到的图像是遵从线性透视规律的. 也就是说，一个物体的宽和高会随着这个物体与相机间的距离增加而按比例变小[14]. 而对于一张矩形的图片，一个物体的宽和高则会根据物体与相机的距离按不同的比例变小. 而这个比例，就是根据相机的焦距得到的，利用针孔模型推导出这个比例关系：

(7)

(8)

其中:x是物体在图像中的宽度，单位：m；w为物体的实际宽度，单位：m；y是物体在图像中的高度，单位：m；f是相机的焦距，单位：像素；d为物体到相机的距离，单位：m；h为该建筑物的实际高度，单位：m.

假设一幅影像x方向无比例尺误差，而y方向比例尺归化系数为1+ds. 此时x方向像片主距若为fx，则y方向像片主距fy为：

(9)

x、y在图像中进行量测所得，有些照片是无法在实地量取w的，最终研究消失建筑的重建，可以根据当地平面图及比例尺获取宽度信息，通过公式(7)可解算出物体与摄像机的距离d，代入公式(8)可解算出建筑物实际高度h. 由于无法获取单像老照片所拍摄的相机型号，故上式的fx、fy是未知的，只能用灭点检校出来的焦距fy=fx=f代替，此为该方法的关键所在.

2 试验结果和分析

2.1 现存建筑对方法验证

验证利用Canon5D Mark IV 固定焦距50 mm相机，选取了一座小型建筑物，拍摄的单张建筑物照片，如图4所示.

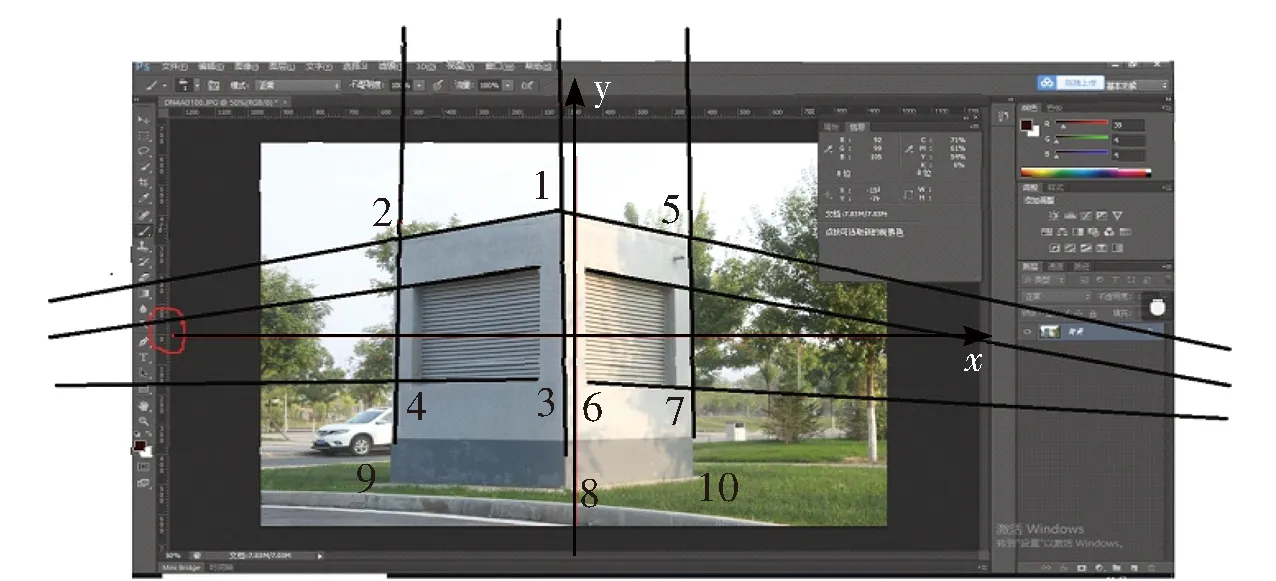
图4 实例示意图Fig.4 Diagram of an example

2.1.1 数据获取

根据图4所示，量得像控点信息见表1.

表1 像控点坐标

经实地量测得到数据见表2.

表2 实地测量数据

2.1.2 数据计算

利用最小二乘直线拟合方法进行线性运算：

根据表3数据，X∞的求解：

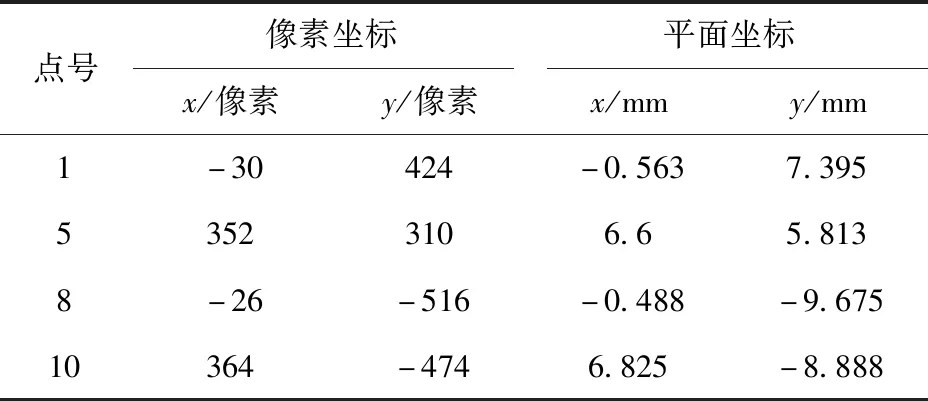
表3 求解X∞量测的数据

求得：l1-5：k1=-0.298，y=-0.298x+7.780，l8-10：k2=0.108，y=0.108x-9.625，灭点X∞=(42.869，-4.995)

根据表4数据，X∞的求解：

求得：l1-2：k′1=0.183，y=0.183x+8.053，l3-4：k′2=0.046，y=0.046x-2.833，灭点Y∞=(-79.460,6.488).

根据表5数据，Z∞的求解：

表4 求解Y∞量测的数据

表5 求解Z∞量测的数据

求得：l1-8：k″1=-235，y=-235x-124.335，l2-9：k″2=50.753，y=50.753x+527.348，灭点Z∞=(-2.281，411.580).

三个正交方向的灭点为：X∞=(42.869，-4.995)，Y∞=(-79.460,6.488)，Z∞=(-2.281，411.580).

像主点坐标的求解：

表6 相关数据

图5 像主点示意图Fig.5 Main point diagram

线性运算：lx∞-2：kX=-2.556，y=-2.556x+104.569，lz∞-1：kZ=25.654y=25.64x+472.408.

得出像主点坐标为：o(-12.95,137.87).

根据公式(2)计算出焦距：

利用matlab自带的camera calibrator功能检校出来的canon5D Mark IV拍摄图4照片的焦距值为：

固定焦距：AV模式下操作，50 mm的ES- 78镜头，调整光圈数值最大为16，继而使光圈最小，将对焦转盘调整至无穷远，将自动对焦AF切换至手动对焦MF，设置ISO感光度为800，设置白平衡模式为AWB模式.

Camera: Canon EOS 5D Mark IV [50.00]全画幅36×24像素大小1 920×1 280.

实际检校：x方向主距：2.585 4e+03(像素)48.47 mm；y方向主距：2.633 9e+03(像素)49.38 mm.

2.1.3 结果

将实际检校的焦距作为真值，灭点求出的焦距误差为4.25%，利用公式(7)、公式(8)最终计算得到该建筑物高3.106 5 m，经实际测量高为3.33 m，其相对精度误差为6.71%. 故验证此方法可行.

2.2 已消失建筑结果

实验地区为现北京建筑大学的前身，学校源于1907年清政府成立的京师初等工业学院，1933年更名为北平市市立高级职业学院，20世纪50年代初期根据北京市政府关于学校调整的决定，该校学生调入校址在复兴门外南礼士路的北京市建筑专科学校. 现什锦花园校园已不存在.

经搜集，获得一些相关老建筑的单张老照片，图6是相对应的影像数据，图7是根据图6照片中的老建筑勾绘出来的三个正交方向的灭点. 相应的地区平面图及其1∶1 000比例尺数据如图8所示，框选区域是什锦花园校园一座二层的教学楼.

图6 老建筑物照片Fig.6 Photographs of Old Buildings

图7 灭点示意图Fig.7 Breakdown Point Diagram

图8 平面图Fig.8 Plane

根据以上灭点法相机标定方法及其高程求取原理,得出图6(一张未知时间、相机型号所拍摄建筑物)规则几何建筑物的高度信息，图7描绘出了老照片三个灭点信息，并进行上述计算，得出此建筑物的高度大约7.23 m. 因此利用单张像片能够获取建筑物高程信息，参考平面图信息可以直接获取建筑物三维信息(约为：长29.6 m、宽7.9 m、高7.23 m)可为三维模型建立提供直接的数据源.

2.3 数字建模

本次试用maya2016软件，根据搜集到的建筑物平面与搜集的照片信息，进行三维模型的实例操作，首先将收集的建筑物各个视图的老照片，分别加载到建模软件各个视图窗口中，依据各视图的照片信息，利用polygon功能进行三维数字重建(图11～图14).

图9 加载矢量图到top窗口Fig.9 Loading vector graphics

图10 加载照片到side窗口Fig.10 Loading photos into to the top window the side window

图11 配准数据Fig.11 Registration data

图12 根据数据进行建模Fig.12 Modeling based on data renderings

图13 模型叠加矢量效果图Fig.13 Model overlay vector

图14 什锦花园教学楼实体模型Fig.14 Solid model of the teaching building of assorted garden

2.4 3D打印

打印中出现的问题及解决方法：

建筑模型屋顶部分都出现了不同程度的缺失、打花打漏现象. 这种情况是由于在建模时没有将屋顶适当加厚导致的. 经过调整，发现当屋顶层厚增加到最初设计片层厚度的3倍时，能达到预期的效果.

模型的制作打印材料是PLA，一种合成固体塑料，在冷却过程中，物体不同部位冷却速率不同，造成内部温度相应较高，而周围散热效果好降热快，不同部位收缩成程度不同，模型会出现不同程度形变和翘边现象. 为了解决这一现实问题，实验使用了特制的3D打印防翘胶水来防止模型翘边现象的发生.

由于机箱的限制，不得不把一些大型建筑物拆开分别打印. 但同时会产生弊端——屋顶与墙体部分比例问题，为了匹配出可以严丝合缝的屋顶与墙体，而不是简单的大致意义上的丈量比对，需要进行多次的实验，确定出最为恰当的尺寸.

2.5 打印成果展示

根据采集的照片，利用灭点法原理进行标定，对图6所示的老照片提取建筑物三维信息，在maya软件中进行建模，最终利用3D打印机将数字模型转换为实体模型，如图15所示，图16是根据搜集到的图8什锦花园校园整体平面图数据及相关照片做成的整体三维模型数据. 注：在3D打印过程中，根据灭点求出的建筑物尺寸打印出来的模型，在高度上不符合人的视觉体验. 因此，3D打印之前需对建筑物高度尺寸参数进行相应修改.