箱梁拆卸满堂支架施工安全控制研究

2019-11-04龙佩恒张佩佩陈雅南曹艳辉

北京建筑大学学报 2019年3期

龙佩恒，张佩佩，陈雅南，吕嘉，曹艳辉

(1.北京未来城市设计高精尖创新中心, 北京 100044； 2.北京建筑大学土木与交通工程学院，北京 100044；3.北京市政路桥股份有限公司, 北京 100068)

近年来我国桥梁行业发展迅速，每年新建桥梁达万余座，与此同时很多旧桥逐渐不能满足使用要求，急需提升改造，其中大部分工程以换梁为主要措施，但目前国内关于大体量旧梁拆卸工程的相关经验较少，且城市发展对施工场所的挤压愈发明显，研究一套快捷、安全、可靠的拆桥方法体系迫在眉睫. 碗扣式支架因其造价低、承载力大、施工时安全稳定、杆件不易产生偏心、施工效率高等优点[1], 在现浇混凝土桥施工中广泛使用. 在旧桥主梁拆卸时也可将其作为临时支撑，但由于支架为临时性结构，计算理论尚未完善，现场施工时一般根据以往工程经验设计，安全意识低[2]. 研究表明，支架失稳倒塌等引起的安全事故占每年施工事故数量的三成左右[3]，以2016 年为例，发生的21 起较大事故中，支架坍塌事故有7 起，死亡人数27 人，占比33.33%. 图1为昆明新机场配套引桥工程在混凝土浇筑施工中支架突然发生垮塌，致7人死亡. 旧桥主梁在拆除时涉及对碗扣式支架的不均匀加载、梁块体系变化等问题，安全风险大，对施工质量要求高，应进行深度研究.

图1 昆明新机场引桥支架倒塌事故Fig.1 Collapse accident of approach bridge bracket in Kunming New Airport

目前，学术界关于碗扣式支架的理论分析有了深层次的进展，取得了大量研究成果. 敖鸿斐[4]通过扣件式支架节点转动实验，分析提取了节点的转动刚度，在有限元计算中引入半刚性节点概念. 杜军荣[5]将碗扣式支架简化为多节间的连续压杆，并验证了其合理性，同时考虑支架体系高度、扫地杆高度和剪刀撑安设等因素，对连续压杆理论计算公式进行修正. 张柳煜[6]分析了支架失稳过程中的荷载- 自振频率关系曲线，为施工中支架的安全监测提供参考.

本文结合昆明市二环路高架桥提升改造工程，依托其63 m箱梁拆卸施工，对临时支架结构的稳定性进行探究.

1 碗扣式支架稳定性分析

1.1 工程概况

本项目为63 m现浇预应力混凝土单箱单室简支桥，桥梁上跨现况滇池路4×13 m下穿通道，如图2所示.

受地下通道限制，无法在其上方架设汽车吊，只能采用满堂支架结合钢管柱的方式拆卸箱梁. 拆除工艺为：搭设满堂支架顶实箱梁箱体底板及两侧翼板，金刚石绳锯切割，汽车吊吊除翼板，箱室采用龙门吊吊运至指定地点. 拆除流程如图3所示.

图3 工艺流程图Fig.3 Process flow chart

箱梁下部搭设普通碗扣式支架，直径为48 mm、壁厚3.5 mm，材料为Q235A；碗扣支架横向外侧使用Φ325 mm(壁厚10 mm)钢管搭设龙门吊轨道支撑梁，两端搭设Φ609 mm(壁厚16 mm)钢管柱. 横桥向布置16根立杆，间距60 cm×4+90 cm×7+60 cm×4，如图4所示，纵桥向按60 cm间距布置，如图5所示. 剪刀撑采用Φ48 mm×3.5 mm钢管四面设置.

图4 支架搭设断面图(cm)Fig.4 Cross-sectional of bracket erection(cm)

图5 支架搭设纵面图(cm)Fig.5 Longitudinal plan of bracket erection(cm)

1.2 理论分析

依据JGJ 166—2016 《建筑施工碗扣式钢管脚手架安全技术规范》将空间碗扣式脚手架横向一榀取为计算单元，同时将整体稳定问题简化为单肢立杆稳定计算，计算公式入下：

N≤φAf

(1)

式中：φ为轴心受压构件稳定性系数；A为杆件截面积；f为钢材强度设计值.

取箱梁最重切割梁块(50.43 t)进行计算. 根据面积分配原理简化计算模型如下：

图6 梁块计算模型图Fig.6 Beam module computing model diagram

依据立杆的截面及材料特性，取单根立杆承载力最大值17.02 kN进行验算. 强度验算：

σ=F/S=34.78 MPa<[σ]=210 MPa

(2)

刚度验算：

σ=34.78 MPa<[σ]=92.4 MPa

(3)

结果均满足要求，满堂支架设置合理，且有很大的安全储备. 但现场施工中在切割箱梁时，局部支架发生了屈曲现象，与计算结果不符合. 综合考虑，有以下原因：

1)满堂支架由杆件节点连接形成体系，杆件之间有相互作用，一根杆件发生变形，必然会引起支架体系的变化. 因此，满堂支架的稳定性分析应综合考虑支架体系的整体性.

2)计算时假设支架为理想直杆，但在实际工程中，支架磨损，材料缺陷等因素对支架影响复杂，用单一的屈曲系数难以反映.

综合以上原因，对满堂支架建立综合整体受力模型，形成整体支架体系受力三维有限元模型，进行详细的受力分析，具体分析过程如下.

1.3 有限元分析

采用Midas/Gen建立整体模型. 基本假定如下：

1) 假定上部荷载施加在立杆轴心上，不考虑偏载；

2) 不考虑地震作用、风荷载等其他水平荷载；

3) 支架连接节点假定为半刚性连接.

碗扣式支架及609钢管柱均采用梁单元建立，横杆与立杆连接处进行梁端约束释放来模拟碗扣支架半刚性节点，支架底端节点边界条件为约束Dx、Dy、Dz，释放Rx、Ry、Rz. 采用Q235钢材，其抗拉、抗压、抗弯强度为205 MPa，弹性模量 2.05×105MPa，泊松比为 0.3. 截面几何特性见表1.

表1 碗扣式支架及钢管柱截面几何特性

支架以上的混凝土箱梁，采用建立板单元方式模拟，将碗扣支架与两端钢管柱连接形成整体结构，如图7、图8所示. 考虑支架节点为半刚性连接，将竖直杆与水平杆节点释放梁端约束. 图9为模型中局部杆件缩小单元后的形状，竖直杆与水平杆、竖直杆与剪刀撑交叉点耦合，水平杆与剪刀撑交叉处不分割不传力. 在板单元上施加初始面荷载，运行特征值分析，在结果中提取一阶屈曲荷载，以此作为特征值屈曲荷载，评估支架体系的稳定性.

图7 模型纵向图Fig.7 Model longitudinal diagram

图8 模型整体图Fig.8 Model block diagram

图9 模型节点细节图Fig.9 Model node detail diagram

特征值分析中将杆件视为理想的轴心受压构件，但实际工程中杆件重复使用，或多或少存在弯曲、磨损、锈蚀，且支架搭设时不可避免会出现偏差，造成结构的偏心等初始缺陷，杆件屈曲问题也不仅仅在弹性范围内. 因此需要对支架结构进行非线性分析，提取的非线性屈曲荷载即为满堂碗扣式支架的失稳临界荷载.

1.4 模型初始缺陷修正

引起支架初始缺陷的因素繁多，大小和分布随机，目前为止还未有统一的计算方法，现行规范中也缺少相关规定[7]. 实际工程中，一般采用一致模态缺陷法进行分析：即将支架结构的一阶屈曲变形模态假设为结构的初始缺陷分布. 支架结构进行特征值分析后，提取一阶屈曲变形模态，乘以合理的修正系数，对修正后的模型进行非线性屈曲分析. 修正系数大小决定了结构几何缺陷的最不利影响，目前大部分资料选取L/400为初始缺陷的修正系数经验值[8].

图10所示，对箱室下部支架单独建模，支架顶端施加100 kN节点荷载， Midas/Gen特征值分析得到一阶模态值为0.510 7，支架的特征值屈曲荷载为0.510 7×100=51.07 kN. 将模型一阶屈曲模态乘以L/400更新模型，在模型顶端施加特征值屈曲荷载51.07 kN替代初始的100 kN，进行非线性屈曲分析. 图11荷载系数- 位移曲线中，荷载系数为0.955 4时，立杆失稳. 计算得到考虑初始缺陷后，整个支架体系的非线性屈曲荷载值为51.07×0.988 4=48.79 kN，相比特征值屈曲荷载降低了4.5%.

图10 箱室下部支架模型Fig.10 Model of lower bracket of cabinet

图11 荷载系数- 位移曲线Fig.11 Load coefficient-displacement curve

2 稳定性的影响因素探究

2.1 主梁切割顺序对支架稳定性的影响

箱梁箱室拆除时在两端设置2(纵向)×3(横向)钢管柱. 箱室拆卸时，先切割箱室两端部，落到钢管柱上，然后在箱室两端钢管柱与碗扣式支架交界处(距梁端7.5 m)及跨中部位同时切割三刀将箱梁落到满堂支架上，最后以6 m间距由两端向跨中切割成小段. 切割中发生3次支撑体系转换：S1：盖梁(刚性支撑)→钢管柱(刚性支撑)；S2：钢管柱(刚性支撑)→碗扣式支架(柔性支撑)；S3：碗扣式支架(柔性支撑)→碗扣式支架(柔性支撑). 由此可见，S2步箱室从钢管柱落架至满堂支架时支撑体系出现变化，必须两端同步切割，均匀加载在支架上，否则箱体两端支撑刚度不一致导致支架竖向变形大小差异，箱室会发生倾斜.

对该桥支架的构造形式进行分析，考虑支架自重，并将箱梁简化为一块无重量的板，在板单元上加载310 kN/m2的面荷载来模拟箱梁自重对支架的压力，建立如表2两个工况，对满堂支架稳定性进行对比分析. 工况一、二切割步序示意图如图12、图13所示.

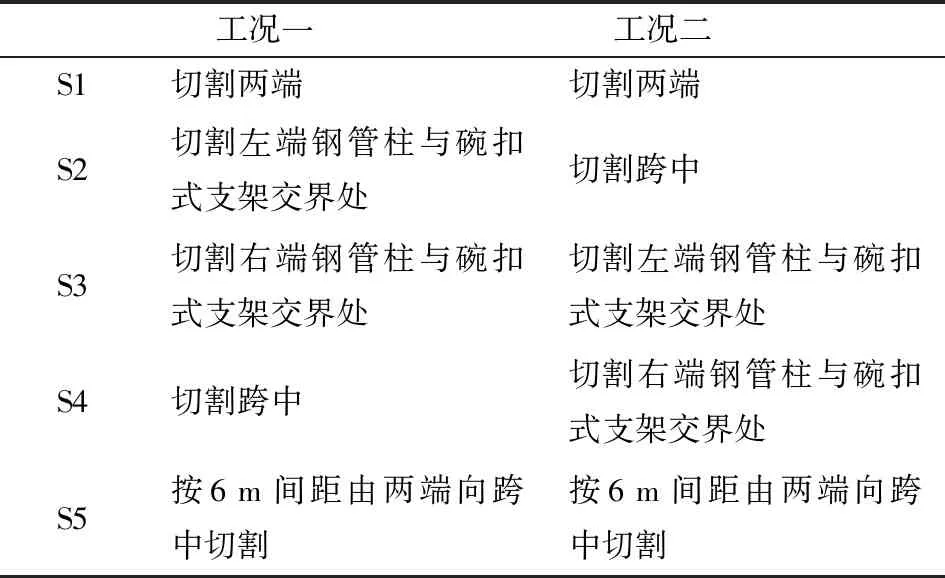
表2 切割顺序工况表

图12 工况一切割步序图Fig.11 Step diagram of bridge dismantling under condition one

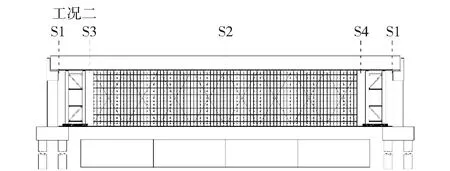
图13 工况二切割步序图Fig.13 Step diagram of bridge dismantling under condition two

提取计算结果可知：

1) 由表3可知，S2、S3时工况二的极限稳定承载力大于工况一，其中S2时工况一的稳定承载力为工况二的75%左右. 由此可见，当箱梁重量由刚性钢管柱支撑转为柔性支架支撑时，首先切割箱梁跨中位置的更有利于体系稳定性.

2) 由图15知，工况一先切割左端时，箱梁左端为支架支撑，右端为钢管柱支撑，钢管柱的刚度远大于支架，因此竖向变形由左向右逐渐增大，箱式呈倾斜状，稳定性减小. 图16中，工况二先切割中间时，竖向变形值相差不大，箱梁更为稳定.

表3 切割顺序不同时非线性屈曲荷载对比

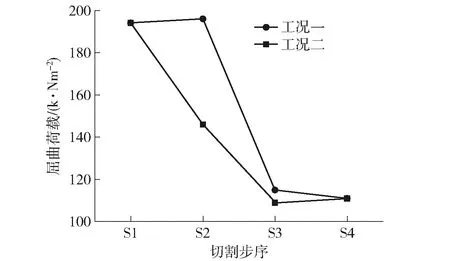
图14 切割顺序不同时非线性屈曲荷载对比图Fig.14 Contrast diagram of nonlinear buckling loads with different cutting sequences

图15 工况一S2阶段一阶屈曲模态图Fig.15 First-order buckling mode diagram of working condition S2

图16 工况二S2阶段一阶屈曲模态图Fig.16 Second S2 first order buckling modal diagram under working condition

分析可得：主梁切割顺序对支架稳定性影响较大，切割不当时会造成主梁的倾斜，可能引起支架倒塌事故. 主梁切割时，应保证两端支撑刚度一致，无法避免时，尽量减小主梁跨度，则减小施加在支架上的荷载，提升支架稳定性. 在本工程中，采用工况二，先切割跨中使得主梁两部分重量相等是最佳方案.

2.2 竖向剪刀撑对支架稳定性的影响

剪刀撑是满堂支架构造的重要杆件，其能使整体结构体系由几何可变体系转化为几何不变体系，能有效地增加结构的抗变形能力，提高结构的整体稳定性. 垂直方向设置剪刀撑起到限制立杆侧向变形的效果，而水平剪刀撑也能够限制满堂支架的平面变形，因此剪刀撑对满堂支架的稳定性至关重要. 剪刀撑影响因素有：剪刀撑跨数、步数；水平剪刀撑设置；中间加强剪刀撑设置等.

据此，取箱梁下部11.4 m×6.4 m×11 m支架建立模型，初始荷载取100 kN，分析以下工况中竖向剪刀撑步数和跨度对支架稳定性的影响差异.

工况一：支架四周布置剪刀撑，纵向9跨×7步，横向7跨×7步，如图17所示.

工况二：支架四周布置剪刀撑，纵向9跨×3步，横向7跨×3步，如图18所示.

工况三：支架四周布置剪刀撑，纵向4跨×3步，横向3跨×3步，如图19所示.

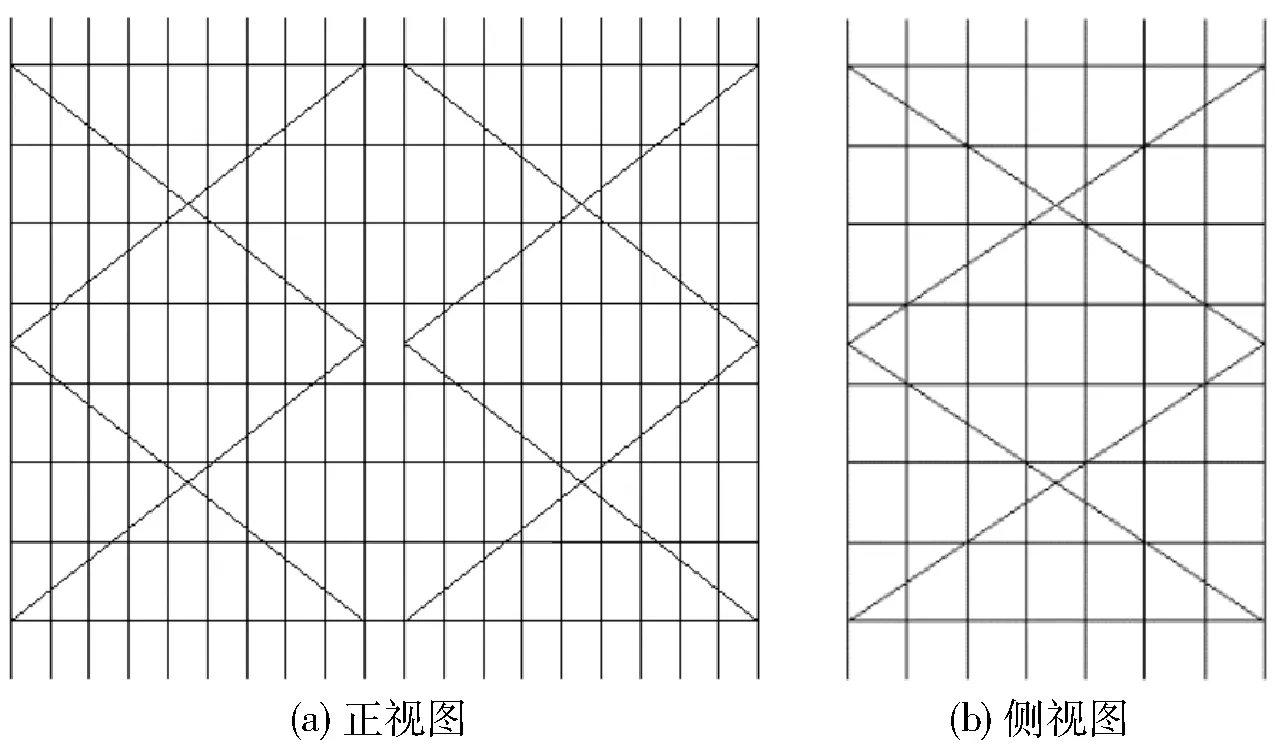
图18 工况二剪刀撑布置图Fig.18 Scissor brace layout of working mode 2

图19 工况三剪刀撑布置图Fig.19 Scissor brace layout of working mode 3

由表4中工况一、二对比可知，竖向剪刀撑步数由7步减小为3步时，屈曲荷载相比增大7.3%；工况三相对于工况二，剪刀撑步数不变、跨度减半，支架稳定承载力减小了3.8%. 由此可知：对于竖向剪刀撑，适当的减小步数、增大跨数可以有效限制立杆的竖向变形，增大稳定性. 本工程建议采取工况二的竖向剪刀撑设置方式.